The problem of long-range correlated dynamic systems has been under study in many areas of contemporary science for a long time. In particular, the statistical properties of biological [1-6] and linguistic [7-10] objects are considered. Usually the DNA and natural language texts are considered as random sequences with finite number of states. There are many methods for describing such systems: fractal dimensions, multi-point probability distribution functions, correlation functions, and many others.

Among other methods, the use of the many-step (high-order) Markov chains is one of the most important because they give a possibility to construct a random sequence with prescribed correlated properties in the most natural way. This was demonstrated in Ref. [11], where the concept of Markov chain with the step-like conditional probability function was introduced.

One of the efficient methods to investigate the correlated systems is based on a decomposition of the space of states into a finite number of parts labeled by definite symbols. This procedure is referred to as coarse graining. The most frequently used method consists in mapping the two parts of states onto two symbols, say 0 and 1. Thus, the problem is reduced to the analysis of the statistical properties of the symbolic binary sequences.

There are three nonequivalent types of the DNA chain mapping onto one-dimensional binary sequences of zeros and unities. The first of them is the so-called purine-pyrimidine rule, {A,G} → 0, {C,T} → 1. The second one is the hydrogen-bond rule, {A,T} → 0, {C,G} → 1. And, finally, the third is {A,C} → 0, {G,T} → 1.

As for the natural written texts, one of the typical coarse-graining procedure was used for mapping the letters onto the binary symbols: .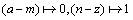

A standard method of understanding and describing statistical properties of a given random sequence of data requires the estimation of the joint probability function of words occurring for sufficiently large length L of words. Unfortunately, for finite size sequences, reliable estimations can be achieved only for very small length L of words because the number mL (where m is the finite-alphabet length) of different words of the length L has to be much less than the sequence length M.

As a plausible model, we use the high-order additive stationary ergodic Markov chain. In Ref. [11] the simple exactly solvable model of the binary N-step Markov chain was presented. The memory length N and the parameter μ of the strength of correlations are the only two parameters of the model. The N -step Markov chain is determined by the conditional probability 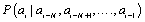of following the definite symbol a_i (for example, a_i=1) after symbols 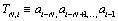The conditional probability pk of occurring the symbol “1” after the N-word containing k unities,

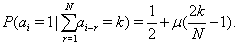(1)

The persistent correlations (μ>0) in the sequence means that each of the preceding symbols a_i-r=1 promotes the birth of new symbol a_i=1 (“attraction” of symbols). Anti-persistent correlations (μ<0) corresponds to the ”repulsion” of symbols.

In order to investigate the statistical properties of binary chain, obtained by mapping DNA and texts, the distribution WL(K) of the words of definite length L by the k number of unities in them was considered, and the variance of k, 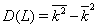was calculated.

It is well-known that the statistical properties of the coarse-grained texts written in any language show a remarkable deviation from the statistical properties of random sequences [9,7]. In Ref. [12] the study of different written texts was performed and it was shown that all of them are featured by the pronounced persistent correlations. It was shown that all variance curves D(L) go significantly higher than the straight line of uncorrelated diffusion, i.e., the persistence is the common property of the coarse-grained written texts at large scales. However, it should be emphasized that regardless of the kind of mapping at small distances, L<80, all curves for D(L) correspond to a slight anti-persistent behavior.

Turning to the DNA sequences, by way of example, the variance D(L) for the coarse-grained text of Bacillus subtilis, complete genome, NC 000964.gbk [13] was calculated for all possible types of mapping. The persistent properties of DNA turn out to be more pronounced than for the written texts and, contrary to them, the D(L) dependence for DNA does not exhibit the anti-persistent behavior at small values of L. However, as well as for the written texts, the D(L) curve for DNA does not contain the linear portion at large scales. This suggests that the DNA chain is not a stationary sequence. In this connection, we would like to point out that the DNA texts represent the collection of extended coding regions interrupted by small non-coding regions (see, for example, Ref. [4]). According to our results, the non-coding regions do not interrupt the correlation between the coding areas, and the DNA system is fully correlated throughout its whole length, in contrast to the generated Markov sequence where the full length M of the chain is far greater than the memory length N. In other words, the coarse-grained texts and DNAs are similar not exactly to the Markov chains but rather to some non-stationary short fragments of the chain.

The noticeable deviation of different curves D(L) for 3 types of mapping [14] demonstrates, in our opinion, that the DNA texts are much more complex objects in comparison with the written ones. Indeed, the different kinds of mapping reveal and emphasize various types of physical attractive correlations between the nucleotides in DNA, such as the strong purine-purine and pyrimidine-pyrimidine persistent correlations, and the correlations caused by a weaker attraction A↔T and C ↔ G.

We would like to note that the origin of the long-range correlations in the literary texts is hardly related to the grammatical rules as is claimed in Ref. [7]. At short scales L ≤ 80 where the grammatical rules are in fact applicable the character of correlations is anti-persistent whereas semantic correlations lead to the global persistent behavior of the variance D(L) throughout the whole literary text.

The authors of the work Ref. [14] studied symbolic dynamic systems, examining them as additive Markov chains, but with the use of more complex model with the conditional probability

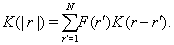(2)

An equation connecting mutually-complementary characteristics of random sequence, memory and correlation functions, was obtained there,

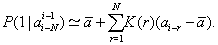(3)

After finding the memory function F(r) on the basis of the analysis of considered sequence correlation function K(r), one can construct the corresponding Markov chain, which possesses the same statistical properties as the initial sequence (Figure 1).

Figure 1: The dependence of the variance D on the length L for the coarsegrained text of Bible (dashed line) for the mapping (a − m) →0,(n − z) →1 and for the coarse-grained DNA sequence of Bacillus subtilis (dotted line) for the mapping {A,G} → 0, {C,T} → 1. The thin solid line describes the noncorrelated Brownian diffusion, D(L)=L/4.

In the paper it was found that the memory function of the DNA and literary texts at long distances is positive and follows the powerlaw decreasing behavior. The coarse-grained texts for eight different literary works was compared. All memory functions can be well fitted by by power-law decreasing functions F(r)=cr^-b. The powers of all curves vary in the interval between b_min=1.02 and b_max=1.56. The powerlaw character of the decrease in long-range correlations in different systems, particularly, in the DNA and literary texts, was mentioned by a number of authors, but it was not associated with the properties of the memory function.

It was demonstrated also that the power-law decrease (without characteristic scale) of the memory function at long distances leads to quite an important property of self-similarity of the coarse-grained texts with respect to the decimation procedure. This procedure implies the deterministic or random removal of some part of symbols from a sequence. The sequence is self-similar if its variance D(L) does not change after the decimation up to a definite value of L. The model of the additive binary many-step Markov chain with the step-like memory function possesses the exact property of self-similarity at the length shorter than the memory depth. As it was demonstrated, the coarsegrained literary texts possess the self-similarity property as well, and this property is connected with power-law memory and correlations.

Another important characteristics serving to the purpose of studying complex dynamics is entropy [15,16], being a measure of the information content and redundancy in a sequence of data. Among fields of science where the notion of entropy is of major significance, natural language processing [17] is the one of the most important.

The using of the Markov chains method makes it possible to calculate analytically the entropy of the sequence [18]. Supposing that the correlations are weak, but not short, we express the conditional probability function by means of the pair correlation function,

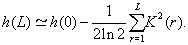(4)

This allow us to represent the differential entropy h(L) in terms of the conditional probability function of the Markov chain and calculate the entropy as the sum of squares of the pair correlators,

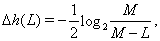(5)

A fluctuation contribution to the entropy due to finiteness of random chains was examined. Since the numerically calculated correlation functions of finite sequences are random quantities, which depend on the particular realization of the sequence, these fluctuations can contribute to the obtained entropy even if the sequence is uncorrelated. As it is shown, the additional correction to the entropy is

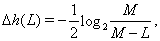(6)

Where M is the length (the number of symbols) of the sequence.

Note that the obtained results allow us to analyze not only coarsegrained DNA and texts (binary sequences), but also the original ones, which are constructed on 4-symbolic and 27-symbolic alphabets.

At first glance, the correlation length of analyzed texts (determined as the length where the entropy takes on a constant value) is of order of 9-11. But after this point one can observe a nearly linear small decrease of entropy extended over 2-3 decades. Probably, this phenomenon could be explained by small power-low correlation discussed above.

In order to evaluate the entropy of the DNAs, we calculate all 9 symbolic correlation functions C_α,β,M(r) of the Homo sapienschromosomeY, locus NW 001842422 [13] and apply elaborated method.

It was shown that the entropy in the interval 7 × 10³4 takes on the constant value, h(L);1.41. It means that for L>2 × 10³ all binary correlations, in the statistical sense, are taken into account. In other words, the correlation length of the Homo sapiens chromosome Y is of the order of 10⁴. This length Rc is much grater than correlation length Rc ≈10 observed for natural written texts (Figure 2).

Figure 2: The differential entropy of Homo sapiens chromosome Y, locus NW 001842422 [13], of length M; 3.9 × 10⁶ vs length L with the fluctuation correction (dashed line) and of the text of Bible (solid line).

In the entropy plot of another locus (NW 001842451) one cannot see a constant asymptotical region, which would be an evidence for the existence of stationarity and finiteness of the correlation length. We suppose that the locus is not well described by our theory at long distances due to the relatively short length of sequence. The fluctuation correction of the differential entropy should be small with respect to the correlation contribution in the region of reliability of the result. Thus, for this sequence only for L<10³ the result can be considered as a plausible.

These results was compared with those obtained by estimation of block entropy where the probabilities of words occurring are calculated with standard likelihood estimation. For the coarse-grained (binary) DNA sequence of R3 chromosome of Drosophila melanogaster of length M; 2.7 × 10⁷ it was shown a good agreement between two approaches for 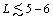units. For four-valued sequence (composed by adenine, guanine, cytosine, thymine) we cannot make a similar conclusion. It is clear that at small L strong short-range correlations or the exact statistics of the short words are more important than that which we took into account - the simple pair correlations.

It is difficult to come to an unambiguous conclusion, which factor, the finiteness of the chain or the strength of correlations, is more important for the discrepancy between the two theories and between the two studied sequences.

Thus, DNA and text sequences possess complex long-range correlated behavior. Comparing their statistical properties, such as variance D(L), memory function F(r) and differential entropy h(L), one can conclude the following:

* The variance D(L) at large scales shows a remarkable persistent deviation from random objects.

* The deviation of the curve D(L) for DNAs is more pronounced than that for the written texts.

* As well as for the written texts, the D(L) curve for DNA often does not contain the linear portion at large scales. This suggests that such DNAs and texts are not stationary sequences.

* At small distances the correlations of DNAs and texts contain anti-persistent region for most of mapping types (the absence of the this effect in DNAs, declared in Ref. [12], turned out inaccurate in next investigations).

* The memory function F(r) of the DNAs and literary texts at long distances follows the power-law decreasing behavior. The powers of this function for texts vary in the interval between b_min=1.02 and b_max=1.56.

* The power-law decrease of the memory function at long distances leads to the self-similarity of the sequence.

* The differential entropy h(L) of the original (not coarse-grained) DNAs and natural written texts indicates more long correlation in DNAs than in texts, but for some samples their size M is not sufficient and the fluctuation contribution (6) to the entropy can exceed the correlation one (5).