Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2013) Volume 2, Issue 4
As part of our recent research to assess the potential of low-cost navigation sensors for Unmanned Aerial Vehicle (UAV) applications, we investigated the potential of carrier-phase Global Navigation Satellite System (GNSS) for attitude determination and control of small size UAVs. Recursive optimal estimation algorithms were developed for combining multiple attitude measurements obtained from different observation points (i.e., antenna locations), and their efficiencies were tested in various dynamic conditions. The proposed algorithms converged rapidly and produced the required output even during high dynamics manoeuvres. Results of theoretical performance analysis and simulation activities are presented in this paper, with emphasis on the advantages of the GNSS interferometric approach in UAV applications (i.e., low cost, high data-rate, low volume/weight, low signal processing requirements, etc.). The simulation activities focussed on the AEROSONDE UAV platform and considered the possible augmentation provided by interferometric GNSS techniques to a low-cost and low-weight/volume integrated navigation system (presented in the first part of this series) which employed a Vision-Based Navigation (VBN) system, a Micro- Electro-Mechanical Sensor (MEMS) based Inertial Measurement Unit (IMU) and code-range GNSS (i.e., GPS and GALILEO) for position and velocity computations. The integrated VBN-IMU-GNSS (VIG) system was augmented using the inteferometric GNSS Attitude Determination (GAD)sensor data and a comparison of the performance achieved with the VIG and VIG/GAD integrated Navigation and Guidance Systems (NGS) is presented in this paper. Finally, the data provided by these NGS are used to optimise the design of a hybrid controller employing Fuzzy Logic and Proportional-Integral-Derivative (PID) techniques for the AEROSONDE UAV.
<Keywords: GNSS attitude determination; Attitude determination and control; Unmanned aerial vehicle; Low-cost navigation sensors; Fuzzy logic controller; PID controller
Technological developments in the realm of satellite navigation have led to innovative concepts in the mission management of current and next generation air, land and sea vehicles. Navigation systems including GNSS or integrated GNSS/INS are being used extensively today in most aerospace platforms around the world and new promising technologies are being explored. The great majority of current manned and unmanned aerial vehicles perform attitude determination tasks by using inertial sensors (ring laser gyros, fibre optics gyros, accelerometers, etc.), packaged into Attitude and Heading Reference Systems (AHRS) or into Inertial Navigation Systems (INS). Although AHRS/INS technologies are well established [1], they have some disadvantages. High accuracy class products are costly when compared with emerging alternative technologies (e.g. MEMS based Inertial Measurement Units), AHRS/ INS position data accuracy degrades with time and their attitude accuracy is strongly dependent on platform dynamics. Furthermore, a significant amount of data processing is required to “smooth-out” sensor errors and extensive simulation, laboratory and ground/flight test activities are often required in order to properly design and calibrate the Kalman Filter parameters. The use of inexpensive GNSS technology for aiding AHRS/INS has been extensively investigated over the past decades, and integrated GNSS/INS systems are the state-of-the-art for aerospace platform navigation applications [2-4]. The concept of replacing traditional attitude sensors with GNSS interferometric processing (carrier-phase) has been also considered in recent years, mostly for spacecraft applications (replacing or aiding traditional sunsensors, horizon-trackers, star-trackers, magnetometers, etc.), and for manned aircraft [5-8] and ship applications [9]. Due to the low volume/ weight of current carrier-phase GNSS receivers, and the extremely high accuracy attainable notwithstanding their lower cost, interferometric GNSS technology is becoming an excellent candidate for future UAV applications [10]. The accuracy of the GNSS Attitude Determination (GAD) systems is affected by several factors including the selected equipment/algorithms and the specific platform installation geometry, with the baseline length and multipath errors being the key elements dominating GAD systems performance [10-12] developed an extension of the known Least-squares Ambiguity Decorrelation Adjustment (LAMBDA) method [13] for solving nonlinearly constrained ambiguity resolution problems associated to GNSS attitude determination.
One of the main challenges of implementing GAD systems for attitude determination in UAV and other aerospace platforms is the need of resolving integer ambiguity in real-time in order to obtain reliable attitude estimations [10]. In recent years several techniques have been developed for integer ambiguity resolution. Giorgi et al. [10] In terms of data rate, Pinchin [8] suggests that a typical AHRS/ INS system provides attitude measurements upwards of 100Hz where as a GAD system output is in the order of 1-5Hz which is too low for high dynamics platform applications. In small UAV platforms a simple solution that integrates a low cost GNSS/MEMS-IMU system for attitude determination may be also affected by vibrations and aerodynamic effects acting on the platform itself (e.g., aeroelasticity). Therefore, a very accurate initial heading estimate or integration with other sensors is often required for stable filter performancein such applications [13]. As a consequence, the integration of additional augmenting sensors such as Vision-based Navigation (VBN) sensors [14,15] can provide significant improvements in the accuracy and continuity of the measurements. Several methods have been developed in the past decades for GAD systems. The classical method, developed by Cohen [14], involves two main steps. The first step is to find a matrix that transforms the baseline configurations to an equivalent orthonormal basis and the second step is the use of fast algorithms (e.g., QUEST and FOAM) for attitude determination. An alternative method is to adopt recursive algorithms to minimize a cost function that links all available carrier phase measurements. Independently from the method selected, since GAD errors are dominated by lengths of the baselines used, some efficient geometric algorithmsare proposed for baseline selection in the presence of redundant satellite measurements. Various controller schemes have also been applied in the past to the design of autonomous control/servoing systems for UAVs. Some of these techniques include Adaptive Control [16-19], Fuzzy Control [17,20], Neural Networks, Genetic Algorithms and Lyapunov Theory [21]. Beyond studying the possible synergies attainable from integration of GAD systems with other low-cost and low-weight/volume navigation sensors (e.g. VBN and MEMS-INS), and additional objective of our research is to develop an hybrid Fuzzy/PID controller using INS, GNSS and GAD input data and also capable of VBN guidance (visual servoing) during the final approach and landing phases of the flight. This is allowing the development of an integrated Navigation and Guidance System (NGS) capable of providing the required level of performance in all flight phases of a small UAV.
In the fundamental concept of interferometric GNSS Attitude Determination (GAD), the measurement of the phase of the GNSS signal carrier allows to determine the relative displacement of the antennae in the body reference frame. This information is directly related to the attitude of the vehicle. The displacement of the antenna baseline (b) with respect to the LOS of the GNSS signal is given by:
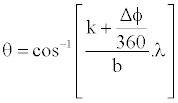 (1)
(1)
Where the phase difference Δφ/360 is proportional to the projection of the baseline (b) on the Line-of-Sight (LOS).Since the antennae are placed at different locations, the phase measurements of the incoming GNSS signal carrier are different for each antenna. By knowing the integer number of cycles travelled by the carrier (N), it is possible to determine the vehicle attitude. When using GNSS for attitude determination it is sufficient that only two satellites are in view due to the following considerations:
• Common time reference: measurements are independent from the error at the receiver clock as it is the same for the measurements performed by each antenna.
• Baseline setting: the relative position of the antennae on the vehicle is known a priori; this eliminates another unknown factor which reduces the number of satellites required.
GAD algorithms
Knowing the coordinates,both in the body reference frame and in the North-East-Down (NED) frame, of the unit vectors of the LOS to the Sn satellites, and the unit vector perpendicular to the plane containing three antennae Â, it is possible to determine the attitude of the vehicle. In the body axis reference frame (x,y,z) any combination of 3 not aligned antennae located at the points P1, P2, P3 originates a plane π. This plane is the locus of points P with coordinates that satisfy the equation:
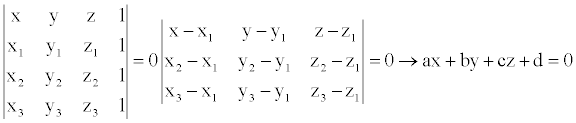 (2)
(2)
Since the plane π is represented by equation ax + by + cz + d=0, the vector of components (a, b, c) is orthogonal to the plane. Therefore, the coordinates of the unit vector  orthogonal to the plane are:
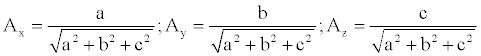 (3)
(3)
From the three antennae located on the plane π, a master antenna M and two “slaves” B with components (B1,B2,B3) and C with components (C1,C2,C3) are defined (Figure 1).
Using the relations to determine the angle between two vectors and between a vector and a plane, the unit vectors from the LOS to satellites (Sn) are those for which the following conditions apply:
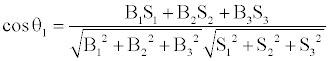 (4)
(4)
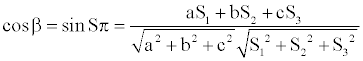 (5)
(5)
 (6)
(6)
 (7)
(7)
From Eq. (5) and Eq. (7), a system of 3 equations with 3 unknowns (S1,S2,S3) is obtained only if the magnitude of the LOS vector is known. The unknowns are the coordinates of vector LOS in the body frame. Then, the angle β, which is the angle between the LOS vector to the satellite Ŝn and the perpendicular  to the plane π, can be obtained directly from equations Eq. (5) and Eq. (7). The unit vectors Ŝn → LOS, known in the body frame, are fully defined in the NED frame (CG, xN, yN, zN). In fact, the receiver extracts the coordinates of the satellite from the navigation message. From these parameters, it computes the unit vector of the LOS in ECI frame. Since the NED frame is always defined with respect to the ECI-frame the unit vectors ŜN are then properly defined in the NED frame. In particular if CEN is the transformation matrix from ECI-frame to NED, the unit vector ŜnN in the NED frame is given by the following transformation:
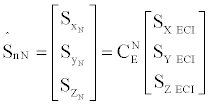 (8)
(8)
The next step is to determine the coordinates of  in the NED frame in order to have a full set of vectors that will be used for attitude determination. Analytically this geometric problem can be represented by a system of 3 equations with 3 unknowns A1, A2, A3. These are the components of vector A in the auxiliary reference frame (x1, x2, x3):
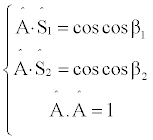 (9)
(9)
By getting
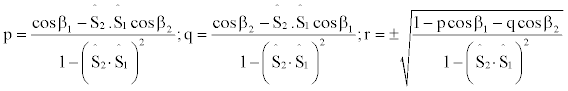 (10)
(10)
The solution of  becomes
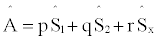 (11)
(11)
Eq. (11) generates 2 possible ambiguous solutions. In order to solve this ambiguity the following steps can be performed:
• Compare the possible solution with an estimation made in advance.
• Compare more attitude solutions that can be accumulated in a certain observation time discarding those which are dispersed.
• Use a third satellite.
The analytical solution of the system with three satellites is given by:
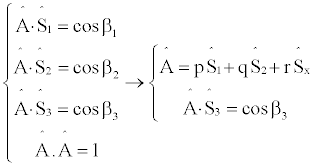 (12)
(12)
Although the system Eq. (12) has a unique solution for  in a real system it is necessary to take into account the possible errors in the determination of the values of Ŝn and βn. The geometry with three satellites and the error values is illustrated in Figure 2.
With the methodology described above, the input data required to determine the attitude states of the vehicle is defined (i.e., the coordinates of the vectors Ŝn and the coordinates of the vectors  in the body frame and in the NED frame). Then two approaches can be used for attitude determination, one is a variant of the classical method [16] that allows the determination of the attitude states by considering one single pair of vectors (e.g.,  and Ŝ1, Ŝ1 and Ŝ2).In order to select the optimal pair of vectors, the errors associated to such combination are considered (the pair with the minimum RMS/RSS error is selected. The recursive algorithm method, uses all available information from 3 nonaligned antennae and 3 satellites (Â, Ŝ1, Ŝ2, Ŝ3), to obtain an estimation of the attitude of the vehicle by minimizing the following cost function:
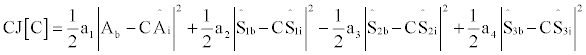 (13)
(13)
Where a1, a2 and a3 and a4 are 4 non-negative weights. Therefore, for a number of N measurements, such a cost function can be generalized as follows:
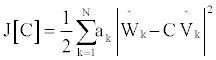 (14)
(14)
Where Ŵk is a vector determined in the body axis frame and 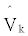 is the corresponding vector in the inertial frame. In the ideal case of absence of errors, each term of Eq. (13) would be cancelled in correspondence to a certain proper orthogonal matrix C. As this does not occur in reality, it is necessary to assign appropriate weights in order to minimize the cost function by considering the accuracy of the measurements. Since only 3 of 9 elements are independent, it is acceptable to minimize the cost function for a minimum number of parameters (e.g., Euler angles), in order to reduce the complexity on the calculation.
is the corresponding vector in the inertial frame. In the ideal case of absence of errors, each term of Eq. (13) would be cancelled in correspondence to a certain proper orthogonal matrix C. As this does not occur in reality, it is necessary to assign appropriate weights in order to minimize the cost function by considering the accuracy of the measurements. Since only 3 of 9 elements are independent, it is acceptable to minimize the cost function for a minimum number of parameters (e.g., Euler angles), in order to reduce the complexity on the calculation.
GAD accuracy
Similarly to Geometric Dilution of Precision (GDOP, the Attitude Dilution of Precision (ADOP) is a parameter that indicates how accurate the attitude solution is. The ADOP is related to the error in attitude calculation σθ, the error in range σr and the baseline length b by the following equation
 (15)
(15)
Where
 (16)
(16)
And  is the matrix 1× n of the LOS to the satellite, n is the number of satellites in view and l the identity matrix. The value of ADOP is generally equal to 1 or less. This indicates that the GNSS constellation guarantees favorable geometry for the attitude determination. Therefore, it is possible to make an approximation of the attitude error by assuming that ADOP=1. With this assumption the relationship is simplified to
is the matrix 1× n of the LOS to the satellite, n is the number of satellites in view and l the identity matrix. The value of ADOP is generally equal to 1 or less. This indicates that the GNSS constellation guarantees favorable geometry for the attitude determination. Therefore, it is possible to make an approximation of the attitude error by assuming that ADOP=1. With this assumption the relationship is simplified to
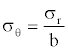 (17)
(17)
By knowing the error σθ associated with each measure, assuming that the measures are statistically independent, it is possible to calculate the total RSS error σTOT by the relation
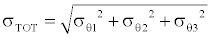 (18)
(18)
The error in attitude determination is a function of the instantaneous orientation of the aircraft, the satellite geometry and the selected baselines. The range error σr in the Eqs. 15 and 17 includes the following contribution:
• Multipath: This is the main source of error. Even though the error is highly deterministic, previous research [22] shows that even with the most careful study on the location of the antennae the error cannot be reduced below the 5 mm threshold. This error is directly dependant on different non-controlled variables such as the environment itself; other variables also influence this source of error, such as materials, antennae gain, geometry, etc. The control of these variables to reduce the error is often complex and expensive.
• Structural distortion: In high temperature applications the vehicle surface may experience thermal deformation. This will cause a relative displacement between antennae with consequent errors in the attitude solution. Aeroelastic effects also introduce structural distortions.
• Tropospheric error: The troposphere is often considered a source of error for the transmission of electromagnetic signals [23,24]. The error becomes more significant with the increase of the refraction index. This increase becomes significant at altitudes . The refraction index causes a deflection of the GNSS signal [25]. The refraction index can be modelled according to Snell’s law. Therefore, an error is introduced when the phase measurements are converted to attitude angles.
• Signal-to-Noise Ratio (SNR): In high dynamics applications the tracking loop bandwidth needs to be extended. By extending it, the bandwidth of the associated error is also increased [26]. Many stochastic models have been proposed based on the SNR reported by the receiver [27,28].
• Specific errors in the receiver: This source of error can become significant if it is not considered at an early design stage. Nowadays, technology allows to have precise models of it [22,29]. There are several examples of those errors such as crosstalk, which is common in antennae with high gain, line bias, which is the phase offset between one antenna and another and inter-channel bias, which results of the phase measurements from different satellites that use a different channel.
• Total error: From the analysis on the different source of errors in range, considering that multipath is the dominant error, a rough approximation to this error is given by:
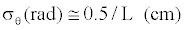 (19)
(19)
Where L is the longitude of a given baseline. In Eq. (19), it is shown that the error appears inversely proportional to the length of the baseline used for attitude determination. Hence it is always preferred to use longer baselines which allow a more accurate attitude solution. A detailed discussion of the sources of errors can be found in the literature [30,31].
Geometric algorithm for antennae selection
As a first step the antennae with less than 2 satellites in view are discarded by using a masking algorithm. It is then when the baselines are measured between the remaining antennae.
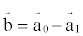 (20)
(20)
By ordering the baselines in descending order there is a selection of the first two that are associated with the greater area of the triangle formed by the baselines and their links. The common antenna with respect to these baselines is identified as possible Master M antenna while the other two are possible slaves: Sl1 and Sl2. Once the process is repeated for all antennae with at least 2 satellites in view the optimal combination of three antennae is selected for those, whose the following function is maximum
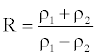 (21)
(21)
Where ρ1 and ρ2 are the lengths of baselines M-Sl1 and M-Sl2
Employing the geometric algorithm for optimal selection of the antenna baselines and the recursive algorithm (Eq. 20,21) for overdetermined attitude computations, the resulting error analysis is presented in Table 1.
| Configuration | 1-σ Pitch Error (°) | 1-σ Roll Error (°) | 1-σ Yaw Error (°) |
|---|---|---|---|
| 3 Antennae | 1.37 | 0.93 | 1.77 |
| 4 Antennae | 0.47 | 0.32 | 0.76 |
| 5 Antennae | 0.38 | 0.52 | 0.54 |
| 6 Antennae | 0.32 | 0.45 | 0.36 |
| 7 Antennae | 0.29 | 0.34 | 0.31 |
| 8 Antennae | 0.27 | 0.23 | 0.22 |
Table 1: GNSS attitude determination errors.
Then the GNSS attitude determination is integrated to the VIG Navigation System as Illustrated in Figure 3.
It can be observed that the output of the GNSS Attitude Determination System (GAD) is integrated to the navigation system extended Kalman Filter for data fusion. The details of the EKF implementation can be consulted in [14,15].
The AEROSONDE model from Unmanned Dynamics LLC was used in the simulation. The AEROSONDE UAV is a small autonomous aircraft used in weather-reconnaissance and remote-sensing missions [32]. This model is part of the Aero Sim Blockset implemented in MATLAB/Simulink® [30]. In addition to the basic dynamic blocks, complete aircraft models are present which can be configured as required. The library also includes Earth models (geoid references, gravity and magnetic fields) and atmospheric models. The inputs to the AEROSONDE model include control surface deflections in radians, throttle input, mixture and ignition. Wind disturbances can be added to the model to simulate variable atmospheric conditions. The model outputs the various aircraft states such as the position in the Earthfixed frame, attitude and attitude rates. In order to perform the GNSS attitude determination for the AEROSONDE, 5 GNSS antennae were selected to optimize the length of the baselines. The baseline lengths are defined in Table 2.
| Antennae | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 100 | 180 | 120 | 200 | |
| 2 | 100 | 100 | 100 | 140 | |
| 3 | 180 | 100 | 100 | 100 | |
| 4 | 120 | 100 | 100 | 130 | |
| 5 | 200 | 140 | 100 | 130 |
Table 2: Baseline Length (cm) of Antennae in AEROSONDE UAV.
The position of the antennae on the AEROSONDE is shown in Figure 4. For the design of the control system, an hybrid approach was adopted allowing the controller to take advantage of the VIG/VIG/ GAD integrated navigation sensors during the other phases of flight. To achieve this, fuzzy logic and PID control strategies were adopted for controlling the UAV. PID is the simplest type of linear controller and is used in most UAV control systems. It is easy to implement and is effective for simple systems. On the other hand, fuzzy logic is a form of multi-value logic based on a representation of knowledge and reasoning of a human operator. In contrast to conventional PID controllers, Fuzzy Logic Controllers (FLC) do not require a model of the system. Therefore, it can be applied to non-linear systems or various ill-defined processes for which it is difficult to model the dynamics. The process consists of four components: fuzzification, fuzzy rule base, inference engine and defuzzification. Fuzzification refers to transforming a crisp set into a fuzzy set using linguistic terms. A fuzzy set is a set without crisp, clearly defined boundary. It can contain elements with only a partial degree of membership. A Membership Function (MF) is defined as a curve that classifies how each point in the input space is mapped to a membership value (or a degree of membership) between 0 and 1. Different types of fuzzy logic membership function exist which include s-function, π-function, z-function, triangular function, trapezoidal function, flat π function rectangle and singleton. An example of this is given in Figure 5a. Let ‘input1’ be a crisp set for the input to the system with fuzzy sets ‘short‘, ‘medium’ and ‘long’. Triangular membership functions are used in this case. It is observed that for ‘medium’, the value 5 has a membership function of 1. The value 3 has a membership function 0.3. Therefore it can be inferred that 3 has a lesser belonging to the fuzzy set ‘medium’ than 5. Similarly an output function ‘output1’ is defined with fuzzy sets ‘left’, ‘centre’ and ‘right’ as shown in Figure 5b.
The second component, that is the Fuzzy Rule base, forms the main part of fuzzy logic. It is based on if-then rules that tell the controller how to react to the inputs. The inference engine applies the fuzzy rule base to the inputs and output. It calculates the output required from the rules and passes this to defuzzification. Defuzzification is the method to obtain the output from the controller. It converts the output fuzzy set value to a crisp set using its membership functions. The UAV controller design was approached by decoupled the dynamic models of the aircraft. This resulted in two complimentary controllers, one for lateral motion and one for longitudinal motion. Before initiating the controller design, the open-loop response of the system was first tested. In open-loop flight, the control inputs were set to a fixed value without any feedback from the aircraft states. It is observed that the UAV is unstable in this condition and settles in a constant bank turn and pitch angle as shown in Figure 6a and Figure 6b. This is due to the propulsion system which causes an unbalanced roll moment and excites the spiral mode.
The lateral controller was first designed to stabilize the lateral dynamics of the UAV. This was followed by the longitudinal controller to control the pitch angle. The overall design was then adapted to perform servoing using the information from the VBN sensors and integrated VIG/VIG/GAD navigation systems. The lateral and longitudinal controllers were implemented on MATLAB using the Fuzzy Logic Toolbox. The Mamdani fuzzy inference system (FIS) from the toolbox was used to create the membership functions. Based on the input and output membership functions, the fuzzy rules were developed that relate the inputs and the output. The membership functions and the rules were modified by trial and error to obtain better responses. Triangular and trapezoidal membership functions were used for the membership functions due to their simplicity and ease of implementation. A rough estimate of the membership functions was used for all the variables which were then modified as required. The membership functions which gave the best results for the roll and pitch responses were selected. Linguistic variables were used to define the fuzzy sets of inputs and the outputs of the controller. The fuzzy sets and the range of the inputs and outputs are shown in Table 3, where VN=Very Negative, VP=Very Positive, VH=Very High, VL=Very Low, SN=Slightly Negative, SP=Slightly Positive, SH=Slightly High, SL=Slightly Low, Z=Zero.
| Input Variable | Fuzzy Set | Range |
|---|---|---|
| Roll Error (in) | VN, SN, Z, SP, VP | -180° to 180° |
| Roll Rate (in) | VN, SN, Z, SP, VP | -40°/s to 40°/s |
| Pitch Error (in) | VL, SL, Z, SH, VH | -90° to 90° |
| Deviation (in) | VN, SN, Z, SP, VP | -512 pixels to 512 pixels |
| Deviation Rate (in) | VN, SN, Z, SP, VP | -600 pixels/s to 600 pixels/s |
| Aileron Deflection (out) | VN, SN, Z, SP, VP | -60° to 60° |
| Elevator Deflection (out) | VN, SN, Z, SP, VP | -60° to 60° |
| Required Roll to correct Deviation (out) | VN, SN, Z, SP, VP | -60° to 60° |
Table 3: Fuzzy sets and range of inputs and outputs.
The lateral controller design was designed with the aim of stabilising the roll of the aircraft during the landing phase. This was required to maintain zero roll during touchdown at the centre of the runway so as to avoid wing-strike on the runway. It also controlled the position of the aircraft with respect to the centreline of the runway. Inputs to the controller were the Roll Error, Roll Rate, Deviation and the Deviation Rate and the output was the Aileron Deflection in degrees. The difference between the current roll angles given by the AEROSONDE model with the required value was used to represent the Roll Error. A gain of (π/180) was applied to the Aileron Deflection to convert it into radians. The flap and elevator deflection were set to zero while the throttle was set to full (one). The mixture, ignition and wind were kept at their default settings. The system was simulated for 200 iterations on Simulink with a required roll of 0°. Various membership functions of the Roll Error and Aileron Deflections were considered in order to identify the most optimal FLC for stabilization. The simulation was then repeated with a required roll of 15°. The fuzzy rules used are as follows:
• If (Roll is Z) then (Aileron_Deflection is Z)
• If (Roll is SP) then (Aileron_Deflection is SP)
• If (Roll is SN) then (Aileron_Deflection is SN)
• If (Roll is VN) then (Aileron_Deflection is VN)
• If (Roll is VP) then (Aileron_Deflection is VP)
The Roll Rate was added to the controller so as to give it a higher degree of control. The membership functions for the Roll Rates were developed using the same methodology used for Roll Error and Aileron Deflection. 25 fuzzy rules were developed for the FLC and their surface representation is given in Figure 7a. A steady-state error and overshoot were observed from the roll response of the aircraft. Therefore, a PID controller was desgined to eliminate these errors. PID tuning was carried out to find the values for the gains which gave the optimal roll response. The deviation from the centerline of the runway was controlled using the roll of the aircraft. The value of the Deviation and Deviation Rate was used by the controller to calculate the Required Roll. A surface representation of the fuzzy rules is given in Figure 7b.
The longitudinal controller was used to stabilize and control the Pitch of the aircraft using Elevator Deflections. Prior to design, it was observed that the pitch angle was stabilized to some extent due to the lateral controller as shown in Figure 8.
The design process of the longitudinal controller followed the same methodology as that of the lateral controller. The FLC was first designed using trial-and-error for the membership functions of Pitch Error and Elevator Deflections followed by the PID controller. A derivative gain was used instead of pitch rates. The fuzzy rules used for the longitudinal controller are given below:
• If (Pitch is Z) then (Elevator_Deflection is Z)
• If (Pitch is SH) then (Elevator_Deflection is SP)
• If (Pitch is SL) then (Elevator_Deflection is SN)
• If (Pitch is VH) then (Elevator_Deflection is VN)
• If (Pitch is VL) then (Elevator_Deflection is VP)
The pitch and roll responses of the controller are shown in Figure 9.
The results show that the pitch and roll converge rapidly towards the required value of zero after a short initial instability. Comparing these results with the uncontrolled response in Figure 6, we can confirm that the controller gives satisfactory results. The simulation showed that the controller is able to correct the attitude disturbances caused by moderate to high wind speeds. However, it was observed that the aircraft became unstable with lateral wind speeds exceeding 20 m/s.
In order to evaluate the performance of the integrated VIG/GAD system in conjunction with the Fuzzy/PID controller, a simulation was carried out using the AEROSONDE UAV platform. A suitable flight profile was defined including a number of representative flight manoeuvres [15]. The duration of the simulation is 1150 seconds.
Figure 10 shows a graphical comparison of the ф (roll) error obtained with the VIG and the VIG/GAD systems. It is observed that the VIG/GAD system, with 3, 4 and 5 antennae provides a significant improvement over the VIG system. Table 4 provides the roll error mean and standard deviation values. The performance achieved with 4 and 5 antennae is similar.
| Phases of Flight | VIG | VIG/GAD 3 Antennae | VIG/GAD 4 Antennae | VIG/GAD 5 Antennae | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | σ | Mean | σ | Mean | σ | Mean | σ | |
| Straight Climb | 2.13E-01 | 3.04E-01 | 2.23E-01 | 1.66E-01 | 2.19E-01 | 1.24E-01 | 2.20E-01 | 1.35E-01 |
| Right Turn Climb | 5.47E-01 | 3.41E-01 | 5.55E-01 | 1.88E-01 | 5.56E-01 | 1.85E-01 | 5.55E-01 | 1.85E-01 |
| Straight and Level | 2.32E-01 | 3.73E-01 | 2.53E-01 | 2.01E-01 | 2.52E-01 | 1.49E-01 | 2.52E-01 | 1.63E-01 |
| Level Left Turn | 1.12E-01 | 2.04E-01 | 1.27E-01 | 1.61E-01 | 1.19E-01 | 1.34E-01 | 1.21E-01 | 1.39E-01 |
| Straight Descent | 1.07E-01 | 2.57E-01 | 9.03E-02 | 2.05E-01 | 9.57E-02 | 1.78E-01 | 9.32E-02 | 1.83E-01 |
| Level Right Turn | -8.86E-01 | 2.81E-01 | -9.18E-01 | 2.69E-01 | -9.23E-01 | 2.42E-01 | -9.21E-01 | 2.48E-01 |
| Left Turn Descent | -5.71E-01 | 1.98E-01 | -6.12E-01 | 1.48E-01 | -6.11E-01 | 1.33E-01 | -6.11E-01 | 1.34E-01 |
Table 4: Roll (ф) error statistics (degrees).
Figure 11 presents a similar comparison for the θ (pitch) angle. There is a significant improvement with the GAD integration. In this case it is also observed that the error decreases significantly when the number of antennae is increased. Table 5 confirms such improvement by showing the values of means and standard deviation for different phases of flight.
| Phases of Flight | VIG | VIG/GAD 3 Antennae | VIG/GAD 4 Antennae | VIG/GAD 5 Antennae | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | σ | Mean | σ | Mean | σ | Mean | σ | |
| Straight Climb | -6.17E-02 | 2.25E-01 | -1.27E-02 | 1.81E-01 | -2.81E-02 | 1.09E-01 | -2.32E-02 | 1.07E-01 |
| Right Turn Climb | 1.45E-01 | 2.23E-01 | 1.28E-01 | 1.24E-01 | 1.22E-01 | 7.84E-02 | 1.27E-01 | 7.34E-02 |
| Straight and Level | 3.15E-01 | 3.67E-01 | 2.89E-01 | 2.78E-01 | 2.85E-01 | 2.41E-01 | 2.89E-01 | 2.40E-01 |
| Level Left Turn | 4.74E-01 | 1.27E-01 | 4.21E-01 | 1.86E-01 | 4.06E-01 | 1.02E-01 | 4.06E-01 | 9.67E-02 |
| Straight Descent | 4.17E-01 | 1.55E-01 | 3.44E-01 | 2.21E-01 | 3.47E-01 | 1.21E-01 | 3.50E-01 | 1.12E-01 |
| Level Right Turn | 4.26E-01 | 1.43E-01 | 3.73E-01 | 2.16E-01 | 3.60E-01 | 1.19E-01 | 3.63E-01 | 1.09E-01 |
| Left Turn Descent | 6.48E-01 | 1.40E-01 | 5.03E-01 | 2.57E-01 | 6.62E-01 | 1.89E-01 | 5.96E-01 | 1.15E-01 |
Table 5: Pitch (θ) error statistics (degrees).
Finally in Figure 12 a similar behaviour is observed for the yaw error. The tendency to improvement versus the VIG system is observed for all phases of flight. Table 6 provides the mean and standard deviation values.
| Phases of Flight | VIG | VIG/GAD 3 Antennae | VIG/GAD 4 Antennae | VIG/GAD 5 Antennae | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Σ | Mean | σ | Mean | σ | Mean | σ | |
| Straight Climb | -7.63E-01 | 2.21E-01 | -1.01 | 2.17E-01 | -8.35E-01 | 2.16E-01 | -8.52E-01 | 2.05E-01 |
| Right Turn Climb | 1.08 | 4.24E-01 | 1.15 | 3.79E-01 | 1.14 | 3.71E-01 | 1.14 | 3.71E-01 |
| Straight and Level | 4.74E-01 | 3.67E-01 | 5.40E-01 | 3.93E-01 | 5.40E-01 | 3.07E-01 | 5.40E-01 | 2.93E-01 |
| Level Left Turn | 2.35E-01 | 2.87E-01 | 2.94E-01 | 3.06E-01 | 2.79E-01 | 2.60E-01 | 2.76E-01 | 2.58E-01 |
| Straight Descent | 2.26E-01 | 3.79E-01 | 2.09E-01 | 3.94E-01 | 2.18E-01 | 3.46E-01 | 2.20E-01 | 3.42E-01 |
| Level Right Turn | -1.74 | 5.74E-01 | -1.84 | 5.40E-01 | -1.85 | 4.95E-01 | -8.18E-01 | 4.90E-01 |
| Left Turn Descent | -1.07 | 3.95E-01 | -1.22 | 3.32E-01 | -1.21 | 3.15E-01 | -1.21 | 3.18E-01 |
Table 6: Yaw (ψ)error statistics (degrees).
In this paper we have investigated the potential of GAD systems for integration in small size UAVs. Processing algorithms have been proposed, which allow a fast and reliable computation of the vehicle attitude data. A recursive algorithm has been proposed for combining multiple attitude measurements obtained from different antenna locations, and its efficiency has been analysed in various dynamic conditions using the AEROSONDE UAV platform as a representative test case. Modelling and simulation activities also considered the possible augmentation provided by GAD to a low-cost and low-weight/ volume VIG integrated navigation system employing a VBN, MEMSIMU and code-range GNSS (i.e., GPS and GALILEO) for position and velocity computations. Integration of the GAD with the VIG system using an EKF was accomplished. Considering the AEROSONDEUAV and a number of possible GNSS antenna network configurations, it was demonstrated that, in a variety of dynamics conditions, the accuracy of the VIG/GAD attitude solution was comparable to the accuracy obtainable with traditional inertial sensors. However, the accuracy could be significantly influenced by the chosen antenna network geometry and the number of antennae available. Compared to the VIG system, the VIG/GAD shows an improvement of the accuracy in all three attitude angles. The magnitude of this improvement varies for each angle and for different flight phases. As expected, as the number of antennae increases, also the accuracy improves. The design of the Fuzzy/PID controller was successfully accomplished. However, during the test activities, it was observed that the Fuzzy/PID controller becomes unstable at wind speeds greater than 20 m/s. In case of pure visual servoing during the approach and landing phase, this would lead to the impossibility of tracking the desired features from the surrounding. Current research activities at Cranfield University are investigating the potential of low-cost GNSS attitude sensors (two or more antennae) in various classes of UAVs and Unmanned Space Vehicles (USVs). Additionally, multipath and shielding problems are being carefully modelled and adequate algorithms are being developed in order to cope with these effects during high dynamics manoeuvres.