Journal of Physical Chemistry & Biophysics
Open Access
ISSN: 2161-0398
ISSN: 2161-0398
Research Article - (2013) Volume 3, Issue 1
We study the propagation of localized excitations in a DNA molecule which takes into account helicity and solvent interaction. The small amplitude dynamics of the model is described by envelope solutions made of breathers. Our solutions drastically depends on the twist angle and solvent interaction. It is found that increasing the twist angle decreases the width of the pulse which can be used for the transportation of energy. Increase the solvent interaction term, increases the width of the pulses while the number of waves train decreases with time. The stability of the solutions has been checked through numerical simulations.
<Keywords: Solvent interaction; DNA polymerase; RNA polymerase; Genetic code
Nonlinear physics and mathematics are well known as rapidly developing fields of science with many interesting applications. One of the applications, namely, the application to DNA science. The DNA strands open for copying and transcribing, by separating the double stranded DNA into two single strands of DNA that each carry the full information. The copying is done by DNA polymerase using the complementarity of base pairs. Similarly the genetic code is read by RNA polymerase and ribosomes that again use the matching of complementary base pairs to translate codons into amino acids. The nonlinear physics of DNA is a rapidly developing field of science.
So, the nonlinear physics of DNA has experienced an enormous development in the previous years. There are many experimental data and theo- retical results published about the nonlinear properties of DNA [1]. The study of the nonlinear physics of DNA began in 1980 when Englander et al. [2] published the article: ‘Nature of the open state in long polynucleotide double helices: possibility of soliton excitations’. This was the first time the concept of nonlinear conformational excitations (or DNA solitons) imitating the local opening of base pairs was introduced. In the article the first nonlinear Hamiltonian of DNA was presented and this gave a powerful impulse for theoretical investigations. Many authors made contributions to the development of this field by improving the model Hamiltonian and its dynamical parameters, by investigating corresponding nonlinear differential equations and their soliton-like solutions, by consideration of statistical properties of DNA solitons and calculation of corresponding correlation functions. The results obtained by them formed a theoretical basis for the nonlinear physics of DNA.
Solitary waves have been proposed to describe the open state of the DNA molecule. Yomosa [3] propose a solitons theory for the open states in DNA and derived Kink and antikink solutions for equation of motion of the sine- Gordon form corresponding to the open states with positive and negative helicities. Sataric and Tuszynsky [4] examined the impact of protein inter- action on the breather dynamics of DNA. Daniel and Vasumathi [5] look for the internal dynamics of DNA lattice. Kink and Kink-bubble solitons have been recently derived from the extended PB model [6,7]. Fouda et al. [8] investigate the helicoidal coupling in a two-component helicoidal model of DNA, and bring out the effectiveness of wave switching between the bending of the molecule and the opening of the base pairs.
DNA albeit homogeneous, is still extremely complex. Several physical considerations lead to consideration of mainly two degrees of freedom, whose activation energies are similar to and lower than those of others [9]: radial openings of the double helix (dominant in denaturation), and rotations in a plane roughly orthogonal to the double helix axis (dominant in transcription). Beyond its original motivation to explain the denaturation transition, the PB model has an intrinsic theoretical interest as one of the simplest one- dimensional systems. The PB model has, however a serious shortcoming because it does not take into account the helicoidal structure of DNA. In more years, the advancement of experimental techniques to study the dynamics of single DNA molecule called for more detailed models, and a rather natural first step in this direction was to formulate models able to consider both the radial and the torsional degree of freedom mentioned above at the same time.
An extended PB model including the helicoidal structure of DNA was discussed by Barbi et al. [10]. Breather-like solution in the radial variable coupled with an angular solution dominated by a nonoscillating kink-like term have been derived. The effect of bending and twisting to modify the elasticity of DNA has been considered previously by Barkley and Zimm [11] and by Marko and Siggia [12], but they did not study the consequence of the base pairs opening. Recently, torsional effects have been modeled by a twist angle between neighboring base pairs stacked along the molecule backbone [13].
Twisting is essential in the model to capture the importance of nonlinear effects on the thermodynamical properties. Accordingly, the equilibrium twist angle is θeq=2π/10.4. The thermally activated excitations of the double helix could be twisted solitons spread over a length of about ten base pairs. Hence, it would be interesting to look the effect of twist angle and solvent interaction on the dynamics of breather-like solutions of the DNA molecule [1,6,14].
Motivated by what have been said above, we report on the analytical and numerical investigations of breather-like solutions of twisted DNA with solvent interaction. As far as we know, only few works have been devoted to the study of breather-like solutions of twisted DNA with solvent interaction. We discuss the common role of the twist angle and solvent interaction on the dynamics of breather-like solutions. The main characteristics of this effects are studied during the propagation. The paper is structured as follows. We present the model and show that the dynamics of the system can described by the nonlinear Schrodinger (NLS) equation. Exact analytical solution are obtained for the twisted DNA with solvent interaction. We present the effect of the twist angle on the different quantities which characterize the breather solutions. Numerical investigations are considered in order to verify the validity and stability of analytical solutions. The impact of the twist angle as well as the one of the solvent are presented.
Model and twist effect on breather-like solutions
Let us start by considering the so-called B-form of the DNA molecule. The hamiltonian of this system can be described by the DPB Hamiltonian for a system of N base pairs, which assumes the pair mates separation yn (for the nth base pair) with respect to the ground state position as the relevant degree of freedom. In its simpler version the DNA model has the form of two straight chains with disks connected to one another by longitudinal and transverse springs. As these are viewed as two parallel chains, the DPB model does not account for helicity. Thus, the one dimensional Hamiltonian can be written as
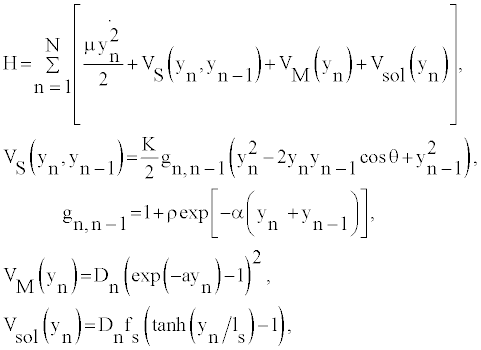 (1)
(1)
where θ denote the twist angle between neighboring base-pairs. VM (yn) describes the energy that binds the two bases of pair n, and VS (yn, yn−1) stands for the stacking interaction between base pairs n-1 and n. Moreover, the heterogeneous DPB model assumes that heterogeneity is essentially carried by different Morse parameters for AT and GC base pairs. Where, the parameters ρ and α are assumed independent of the type of base at the n and n−1 sites and such homogeneity assumptions do not change substantially the thermodynamical properties in the considered denaturation range. The harmonic stacking coupling K is related to the reduced mass μ by K=μν2, ν represents the frequency of the phonon mode. The other parameters of the model are, ρ = 1, α=0.35 Å−1, and K=60 meV Å−2 [15-17]. The base pair hydrogen bonds are modeled by the Morse potential in Equation (1): VM (yn). More explicitly the dissociation energy is given by, Dn=30 meV for AT base pairs, and Dn=45 meV for GC base pairs. ATbase pairs have larger displacements than GC-base pairs, then the inverse lengths are taken as aAT=4.2 Å−1 and aGC=5 Å−1. While the path integral method naturally operates a truncation of the path configuration space [13,15], the problem is treated analytically by adding in Equation (1) a solvent interaction term Vsol (yn) [13,18,19] modulated by a barrier factor fs and by a length ls setting the range of the potential. The solvent term has the effect to enhance (by fsDn) both the energy of the equilibrium configuration and the height of the barrier below which the base pair is closed.
The solvent potential combined with the Morse potential results in a (Figure 1) single barrier of height and width of the orders of fsDn and λs, respectively, as shown in Figure 1. We will refer to the Hamiltonian with the base-pair interaction of Equation (1) as to the Morse-solvent Hamiltonian.
We derive from the Hamiltonian, the equation governing the local oscillations of DNA nucleotides:
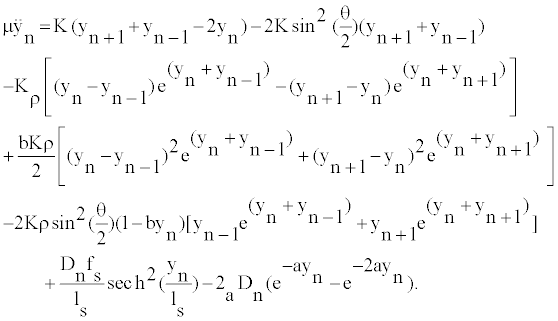 (2)
(2)
It is assumed that the oscillations of bases are large enough to be anharmonic, but still insufficient to break the bond since the plateau of the Morse potential is not reached. Thus, it is presumed that the base nucleotides oscillate around the bottom of the Morse potential. In this respect, we can assume 0
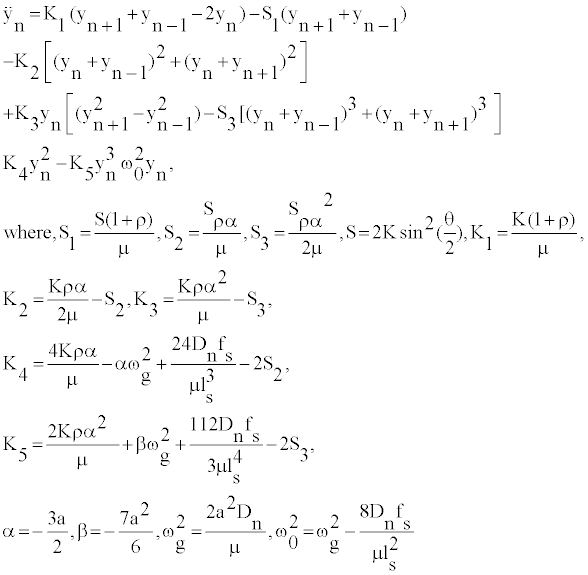 (3)
(3)
For the small, but yet nonlinear oscillations of the nucleotides at the position n we can assume [20,21]:
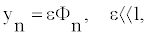 (4)
(4)
which means that the nucleotides oscillate around the bottom of the Morse potential well. However, those oscillations are still large enough to be enharmonic. To obtain the function Φn, we use the semi-discrete approximation [20,22] and look for the wave solution to be a modulated solitonic wave:
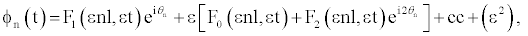 (5)
(5)
where cc stands for the complex conjugate and θn = nql−ωt, l is the distance between neighboring nucleotides of the same strand, ω is the optical frequency of the linear approximation, q=2π/λ is the wave number of a carrier wave. The functions F0 and F2 can be expressed through F1, while the function F1 is a solution of the following equation [20,23]:
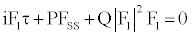 (6)
(6)
where τ and S are rescaled time and space variables. Equation (6) is the (Figure) nonlinear Schrodinger equation. The coefficients of Equation (6) are given by
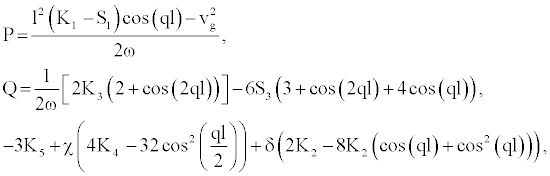 (7)
(7)
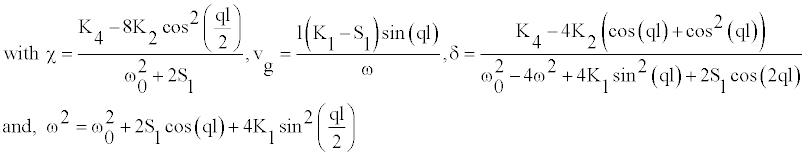 (6)
(6)
Figure 2 plots the dispersion relation versus the wave number q for different values of the twist angle _. Let us use the standard semi-discrete approximation [20] i.e., restrict ourselves to excitations that consist of a slowly varying envelope solution by modulating a carrier wave, with the dispersion relation of a nonlinear wave.
Figure 3 depicts for different value of _, the dispersion coefficient P (Figure 3a), the nonlinear coefficient Q (Figure 3b) and product PQ (Figure 3c), as a function of the wave number of the carrier wave q. From figure 3c we note that, for θ<π/2 the product PQ>0 in the range 0
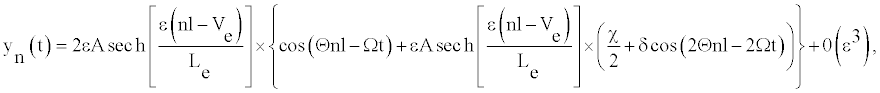 (8)
(8)
Where the amplitude A and the width Le have the forms:
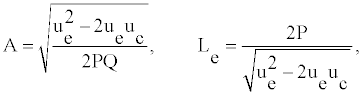 (9)
(9)
With
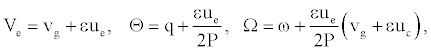 (10)
(10)
vg is the group velocity, ue and uc are the velocity of the envelope and the carrier waves, respectively. As DNA is a dispersive system the group velocity vg can be obtained from the dispersion relation ω=ω(q). Solutions (8) are plane wave solutions, which are unstable because of modulation (or Benjamin-Feir) instability, and a local envelope solution with a vanishing amplitude at the wing. Such a solution has the appropriate shape to represent breathing modes in DNA. One notes that this solution depends on the twist angle as well as on the solvent interaction term.
Let us use the parameters Ue and η defined as:
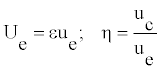 (11)
(11)
The parameter η represents a measure for modulation. The width Le and the amplitude A0 can be rewritten as
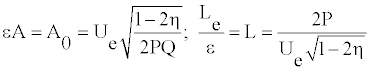 (12)
(12)
From this equation one sees that _ belongs to the interval [0; 0:5]. The signal is modulated if _ is close to its limits of 0.5. To determine the value of of the parameter Ue, one assumes a coherent mode [21,23] for which the envelope and the carrier wave velocities are equal, i.e.
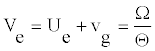 (13)
(13)
Consequently, the function y(t) is the same at any position n. The wave preserves its shape in time. We can easily obtain Ue as follows
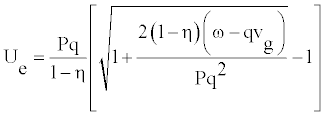 (14)
(14)
The amplitude will be given by
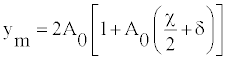 (15)
(15)
The amplitude ym is shown in figure 4 for different valuer of q as a function of θ. Figure 4 shows that the maximum amplitude increases with increasing value of θ provided that q<π/2. But, the maximum amplitude is a decreasing function of θ for q>π/2. For angles around 0.5π, the amplitude increases/decreases exponentially and one can observe big fluctuation describing openings/closing of bases pairs, even to weak temperature. The twist θeq is found to yield the highest stability also for other sequences obtained by varying order and relative content of AT- and GC-pairs. The equality of velocities defined in Equation (13) brings about the equality of the densities of internal oscillation D0 as [21,23]
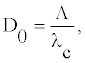 (16)
(16)
where Λ and _c are the length of the envelope and the wavelength of the carrier wave, respectively. To be more precise, this is a number of the carrier wavelengths per an envelope
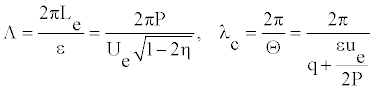 (17)
(17)
So, Equation (16) takes the form
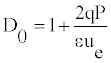
D0 describes the solitonic solution y(nl) which is Equation (8), for a particular value of t. One can also define the density of internal oscillations (density of carrier wave oscillations) Γ0 as a ratio of two periods
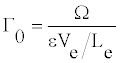
But, for vg>>ue, which might not be always correct, one easily obtains
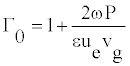
Figure 5 displays the spatial evolution of the transverse stretching yn for different value of the twist angle. These breather-like solutions have been previously obtained through the DNA molecule [22]. One sees in this case that the dynamics of the breather-like solutions depend on the twist angle. Numerical simulations have shown that discrete breathers, which are spatially localized nonlinear oscillations, can appear in models of crystal, biomolecules , and many others nonlinear discrete systems [24,25]. Recently, attention was focused on the dynamics of large amplitude localized excitations in DNA, in which the double helix fluctuates between an open state and its equilibrium structure. These oscillatory states, also called breathing modes or fluctuational openings, are expected to be precursor states for the local denaturation observed during DNA transcription or thermal denaturation.
Figure 6 illustrates the dependence of Ue, λc, Λ, D0 and Γ0 with the twist angle _. We remark that all these quantities which characterize the breather-like solutions are function of the twist angle.
Numerical analysis and twist angle/solvent effect
The results discussed in the previous section are only approximated ones since they are obtained not from the initial equations of motion (2) but from the NLS equation (6) derived after some hypothesis. The lifetime of the solutions determined above is an important parameter, because only long lived excitations can be detected experimentally. We now discuss briefly the numerical technique. We simulate the equation of motion with a fourth- order Runge-Kutta scheme. We choose absorbing boundary conditions to avoid an artificial large amount of radiation s that can affect the creation process and the dynamics of localized structures. Under these boundary conditions, the time step has been chosen to conserve the energy to an accuracy better than 10-6 over a complete run. Most of the simulations are performed with a molecule of N=600 base pairs and we use initial conditions given by Equation 8. It was explained above that the main purpose of this paper was to bring out the impact twist angle and the one of solvent interaction [26]. As a first case, let us study the effect of θ on the dynamics of the system (fs=0). Figure 7 shows the temporal behavior of the breather solution through the twisted DNA molecule for different values of the twisted angle θ. Figure 7a represents the untwisted DNA molecule (θ=0), figures 7b-d, have been, respectively, plotted for θ=θeq , θ=0.25π and θ=0.45π. The temporal evolution of waves depict that, as θ increases, the width of the pulse becomes more narrow while the amplitude of the pulse grows. The transmission of conformational changes over large distances along the double helix have been discussed by Polozov and Yakushevich [27]. They show that nonlinear solitary waves are a suit- able model for describing the transmission. Also, nonlinear solitary waves can be used as regulatory signals propagating along DNA to the problem of gene regulation. Figure 7 shows that the twist angle could be used to control the width as well as the amplitude of waves propagating through the molecule.
Let us now examine the effect of the solvent interaction along the molecule (θ=0). Figure 8 shows the results of this study. If we compare Figure 7a (θ=fs=0), we see that the solvent interaction bring a modulation between pulses, while only the maximum amplitude of the pulses were uniform, the solvent interaction increases the width of pulses while the amplitude certain pulses increases with time as shown in figure 8a. As fs increases, the number of pulses decrease with time as depicted in figure 8b. The base pair displacements should become large enough to yield those fluctuational openings which are peculiar of the double helix dynamics and, at the same time, too large base pair fluctuations should be discouraged as they destabilize the system already at room temperature. The stacking potential has the capability to select the appropriate fluctuation amplitudes as a function of the twist.
Now, we study the combine effect of the twist angle and solvent interaction on the twisted DNA with solvent interaction (θ=0 and fs=0). Figure 9 presents the results of this study for different values of θ and fs. One sees in figure 9 that, the combine effect of these two terms are recovered along the molecule. When fs is took into account, the pulses become broad. While θ increases, the width of the pulses becomes narrow and the amplitude of increases. Figures 9a and 9b have been plotted for θ=0.25π and fs=0.1, fs=0.3, respectively. While figures 9c and 9d have been obtained for θ=0.45π and fs=0.1, fs=0.3, respectively.
We have considered the twisted DNA with solvent, looking for solitary wave excitations. In the semi-discrete approximation, the motion equation of the molecule has been reduced to the NLS equation. The twist angle and the solvent interaction term introduce some modification in the nonlinear co- eï¬?cient Q as well in the dispersion parameter P. Then, envelope soliton solutions of the NLS equation have been obtained. The condition for the existence of these solutions have been obtained and depend on θ. These solutions have been affected by the presence of the twist angle. Increasing θ decreases the width of the pulse while the amplitude increases. Numerical experiments have been carried out in order to verify the analytical predictions. It has been observe that the obtained solutions are stable during the propagation. The impact of the twist angle as well as the one of the solvent interaction term have been investigated. It is found that while increasing θ leads to ultra short pulses, fs leads to broad oscillation s which correspond better to the fluctuational openings of DNA.
The figures 5 and 7 show that, for the small twist models, θ θeq, large fluctuations are possible; Hence, such large fluctuations do contribute to denaturation of molecule. It follows that molecules with small twist have scarce stability and begin to denaturate below room temperature [13]. On the other hand, in large twist models with θ θeq small fluctuations have stacking energies which are higher than the hydrogen bonds dissociation energy hence, their contributions to the denaturation become vanishingly small.
AM and RLW acknowledge the Abdus Salam International Center for The- oretical Physics (ICTP) Trieste-Italy for the �nancial support through the Associate Program.