Journal of Oceanography and Marine Research
Open Access
ISSN: 2572-3103
ISSN: 2572-3103
Research Article - (2016) Volume 4, Issue 2
Dense beds of filter-feeding mussels can exert a considerable grazing impact on phytoplankton in many marine areas depending on downmixing promoted by current, wave- and wind action. But downmixing may also be promoted by biomixing caused by the action of the strong exhalent jets of water from the mussels. Here we study the strength of biomixing exerted by large actively filtering blue mussels Mytilus edulis in stagnant water. Vertical concentration profiles of added algal cells (Rhodomonas salina) were measured (as chl a) over a 70 cm high and stagnant water column in an aquarium above a population of 48 ind.m-2 of mussels of shell length 69.5 ± 2.3 mm. Due to the intense agitation (biomixing) generated by exhalant jets of the actively feeding mussels the profiles remained nearly uniform over the full water column while decreasing exponentially with time, reaching a level of about 40% of the initial level after 120 min, which implied a population filtration rate of about 0.3 m3.h-1.m-2 in agreement with prior clearance measurements. Comparing to numerical solutions of a one-dimensional diffusion model, varying the eddy diffusivity, a value of D = 550 × 10-6 m2.s-1 was estimated. This high strength of biomixing far exceeds those of previous similar studies on the filter-feeding polychaete Nereis diversicolor (0.3 × 10-6 m2.s-1) and the ascidian Ciona intestinalis (150 × 10-6 m2.s-1) and suggests that biomixing in moderate benthic boundary layer flows past mussel beds may contribute to the downmixing of phytoplankton.
<Keywords: Benthic filter-feeders; Exhalant jets; Concentration profiles; Eddy diffusivity; Diffusion model
Filter-feeding bivalves have a considerable grazing impact on the phytoplankton biomass in many shallow marine areas, and dense beds of the blue mussel Mytilus edulis can filter more than 100 m3.d-1.m-2 [1- 3]. However the food uptake depends significantly on the downmixing of biomass which is promoted by external current, wave- and wind action that produce turbulence in the overlaying water [4-6]. However, downmixing is also promoted by biomixing, which is the agitation of the near-bottom water by the action of the fairly strong exhalent jets of water from M. edulis found to be about 8 cm.s-1 and independent of shell length [7] serving also to prevent once filtered water from reentering the animals [8,9].
In the absence of externally generated turbulence and flow such biomixing has been studied above dense populations in benthic filterfeeding polychaetes Nereis diversicolor and ascidians Ciona intestinalis kept in an aquarium [10,11]. From an initially uniform concentration of food particles a food depleted boundary layer was found to grow in thickness with time above the bottom. Comparison of measured concentration profiles to those calculated from a simple diffusion model [8] led to estimates of an effective diffusivity (of the order of 1 to 100 × 10-6 m2.s-1) ascribable to the process of biomixing. With reference to these magnitudes of diffusivity it was conjectured that biomixing would likely be of importance also for turbulent benthic boundary flows of moderate strengths, a conjecture that was confirmed by laboratory flume studies [12] where velocity, turbulence and concentration profiles were measured above a dense bed of Mytilus edulis at 2 flow speeds (0.04 and 0.08 m.s-1) and 3 levels of mussel filtration activity (maximal, reduced and zero). When filtration activity was changed from zero to maximum, profiles changed from those typical of flow over a rough wall (represented by the inactive mussels) to profiles with reduced velocity and increased peaks in turbulence intensity and Reynolds shear stress near the bed, and with an estimated 50% increase in shear velocity. Similar changes in profiles have also been reported by van Duren et al. [13] and discussed by Maar et al. [5] that included increased turbulent mixing due to the combined effect of roughness of shells and biomixing above a mussel bed in a physical water column model suggesting eddy diffusivities of the order of 100 to 250 × 10-6 m2.s-1 due to currents. However, in situations with stagnant water (no currents or wind-driven mixing) the grazing impact of mussels is solely determined by the strength of their induced biomixing.
Here we study the strength of biomixing exerted by large actively filtering blue mussels. We present experimental data on transient concentration distributions in the stagnant water above a bed of mussels in an aquarium and interpret the results in terms of a diffusion model with an eddy diffusivity representing the biomixing induced by the exhalant jets of mussels.
Laboratory clearance and biomixing experiments
Repeated biomixing experiments with initially 46, then 23, and finally 12 blue mussels were carried out prior to the experiment reported here in order to refine the experimental design so that the reduction rate of added algal cells was sufficiently low in order to enable the measurement of a number of vertical concentration profiles above the mussels, typically with a time interval of 15 min. Further it was desirable that the number of open and actively filtering mussels could be observed and noticed in order to compare the experimentally measured filtration rates with maximum estimated rates. These prerequisites could only be fulfilled with a limited number of mussels, but all the experiments conducted with various numbers of mussels showed a similar strength of biomixing as reported here for an optimally controlled experiment with relatively few mussels.
Blue mussels (Mytilus edulis L.) were collected in the inlet to Kerteminde Fjord, Denmark, in March 2015 and placed in an aquarium, 0.5 × 0.5 m2 cross-section by 0.7 m high, containing V = 175 l seawater (20 psu, 19°C). Twelve mussels (mean shell length = 69.5 ± 2.3 mm) were placed on the bottom at position z = 0 cm. By means of a probe (YSI 650 MDS Multiparameter Display System connected to a computer with the software programme EcoWatch) the concentration of added algal cells (Rhodomonas salina) was measured (as chlorophyll a, uncertainty of measurements ± 8%). The probe could be positioned at 10 cm intervals starting at z = 0 cm and ending at the free surface at z = 70 cm. The biomixing experiment was performed with mussels in stagnant water (no air-mixing) and the vertical algal-concentration profile above the mussels was measured with a time interval of 15 min during 2 h. Prior to the biomixing experiment, algal cells were added to the strongly air-mixed aquarium in order to stimulate the mussels to open their valves and at the same time measure the clearance rate of observed fully open mussels. By measuring the reduction in chl a concentration over time, the individual filtration rate (Find) of the mussels was determined from the exponential decrease in algal concentration (verified as a straight line in a semi-ln plot) as a function of time using the equation Find = V × b/n where n = Number of open and actively filtering mussels, b = Slope of regression line in semi-ln plot for reduction in algal concentration with time.
Diffusion model
The transport (downmixing) of algal cells to mussels at the bottom of the aquarium is assumed to be governed by a transient, onedimensional diffusion process without any bulk motion, given by
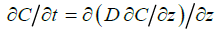 (1)
(1)
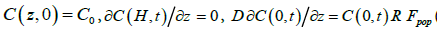 (2)
(2)
Here, C(z,t) denotes the average algal concentration in the aquarium at height z above the bottom at time t and D is the eddy diffusivity associated with the agitation (biomixing) generated by the exhalant jets from the mussels. At t = 0 the initial concentration is assumed to be uniform at C0. For boundary conditions, the downward flux of algal cells is zero at the free surface (z = H) while it is determined by the population filtration rate Fpopand particle retention efficiency R of mussels at the bottom (z = 0). The blue mussels’ retention efficiency of the about 6 μm diameter Rhodomonas salina cells is 100% [14].
Further, to make a clearance analysis of data during the transient process it is useful to integrate Eq. (1) subject to Eq. (2) over the water column, yielding the overall conservation of algal cells as
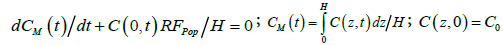 (3)
(3)
where CM denotes the average vertical concentration at any time. For the case of C(0,t) ≈ CM(t), corresponding to vertically well-mixed states, the solution to Eq. (3) is
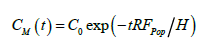 (4)
(4)
The experimental study consisted of clearance measurements to determine filtration rates followed by concentration measurements during transient biomixing in the aquarium. Results from the clearance measurements in the well mixed aquarium are shown in Figure 1 and Table 1, giving filtration rates and increasing number of actively filtering mussels. The mean individual filtration rate was measured to be Find = 5.87 ± 1.51 l.h-1 (Table 1). This value may be compared to the estimated maximum Fest = 9.5 l.h-1 (using shell length L = 69.5 mm in FL = 0.00135 L2.088 [15]) indicating that the actual filtration was about 62 % of the maximum. The average population filtration rate was Fpop = 0.230 ± 0.04 m.h-1 (Table 1).
| Exp. No. | Slope dlnC/dt | n | Find (l.h-1) | Fpop (m.h-1) |
|---|---|---|---|---|
| 1 | 0.0065 | 8 | 8.53 | 0.273 |
| 2 | 0.0043 | 9 | 5.02 | 0.181 |
| 3 | 0.0051 | 10 | 5.36 | 0.214 |
| 4 | 0.0051 | 11 | 4.87 | 0.214 |
| 5 | 0.0064 | 12 | 5.60 | 0.269 |
| Mean± SD | 5.87±1.51 | 0.230±0.04 | ||
Table 1: Clearance experiment (Mytilus edulis). Slope of regression line (Figure 1, upper), average filtration rate of mussels (Find) and population average (Fpop) for the 0.5×0.5 m2 area of the aquarium of volume V = 175 l, n = Open and actively filtering mussels.
Figure 2 shows the transient concentration profiles C(z,t) measured at 10 cm intervals over height z = 0 to 70 cm above the mussels, starting from a uniform concentration of C0 = 4.0 μg chl a l-1. Within the relatively large data scatter, concentrations at all heights decreased in nearly the same manner, on the mean given by the shown exponential regression curve. Comparing to Eq. (4), with H = 70 cm and assuming 100% retention efficiency (I = 1), the estimated average population filtration rate becomes Fpop = 0.0073 (min-1) × 70 (cm) = 0.307 m.h-1 = 7.36 m3.d-1.m-2, which may be compared to the values in Table 1. Given the number of actively filtering mussels to be 12, the average filtration rate of the 69.5 mm mussels is estimated to Find = 0.307 × 1000 × 0.25/12 = 6.40 l.h-1 which is 67 % of the maximum estimated value of 9.5 l.h-1 given above.
The vertical, nearly uniform normalized concentration profiles C(z,t)/C0 in Figure 3, extracted to 15 min intervals by interpolating from the data in Figure 2 that are recorded at odd times, suggest strong vertical biomixing above the mussels over the full water column. These results are used to parameterize the values of D and Fpop in a numerical study of solutions to Eq. (1) and Eq. (2). This leads to the model results shown in Figure 4 for estimated values of eddy diffusivity of D = 550×10-6 m2.s-1 and population filtration rate of Fpop = 0.307 m.h-1.
Figure 1 emphasizes the importance of adding algal cells to stimulate the mussels to open their valves prior to biomixing experiments. The difference in filtration rate of individuals obtained in the air-mixed clearance experiment (Find = 5.87 l.h-1, Table 1) and in the stagnant water biomixing experiment (Find = 6.40 l.h-1, Figure 2) is small, indicating that the biomixing alone was sufficiently strong to fully mix the whole water volume in the aquarium.
Figure 2: Biomixing experiment (Mytilus edulis). Measured concentration profiles versus time at different heights z, C(z,t) (symbols), the mean Cmean(t) of these (black open circles) and their exponential regression curve (dashed black curve) with equation given, leading to Fpop = (0.0073 × 0.7 × 60 =) 0.307 m.h-1, and Find = (0.0073 × 175 × 60/12) = 6.40 l.h-1.
The rate at which the concentration (on the mean) decreases with time (Figure 2) is essentially determined by the magnitude of the population filtration rate. On the other hand, the high degree of vertical uniformity of decreasing concentration profiles (Figure 3) is determined by the high value of eddy diffusivity associated with biomixing which has little or no effect on the rate of concentration decrease. The last concentration level at t = 120 min (C(z,t)/C0 slightly above 0.4) in Figure 4 appears to be reasonably well matched for the population filtration rate Fpop = 0.307 m.h-1 obtained from the exponential regression curve in Figure 2.
A possible gravitational settlement of the algal cells has been ruled out by a parametric numerical study based on the solution of Eq. (1) with the convective term –Vs ∂C/∂z added to the left of Eq. (1) and to the last boundary condition of Eq. (2), where Vs denotes the downward directed settling velocity. Here, any significant value of Vswould shift concentration profiles downward to lower values than observed; in the same manner as would an increased value of RFpop. Any decrease of the eddy diffusivity would not affect the rate of decrease of mean profiles but merely make the profiles less uniform in contrast to observation. Nevertheless the data in Figure 3 show a consistent decrease in concentration near the free surface (over range z = 60-70 cm), particularly during the early part of the experiment, which can only be explained by local gravitational settlement unless an experimental artifact.
Prior to the biomixing experiment the aquarium was well airmixed to ensure an initially uniform concentration of algal cells. To rule out the possibility that it was the eddy diffusivity associated with this initial turbulent state that prevailed during the experiment we determine the rate of decay of this initial turbulence. For an estimate, consider the equations of the K, ε-model for decaying turbulence in the absence of any source of production, see e.g. [16]. Assuming that the eddy diffusivity is of the same order of magnitude as the turbulent viscosity of this model it may be shown to decay with time as D ≈ t-1.07 implying that the ratio of eddy diffusivities at two times, D2/D1 = (t2/ t1)-1.07, would suggest a reduction of D to about half its value during time from 15 min to 30 min, for example. This is clearly not the case to judge from the shape of concentration profiles in Figures 3 and 4 so the constant and high level of eddy diffusivity is due to the biomixing generated by the mussels.
Table 2 shows some characteristic parameters of 3 experimental biomixing studies: Nereis diversicolor [10], Ciona intestinalis [11], and Mytilus edulis presented here. The population density of animals (Npop), which under favorable conditions directly determines the population filtration rate, was chosen to be close to conditions found in the field in the two first studies but rather low (Npop = 48) in the present study to avoid interference or competition between animals and to ensure that the half-life of added algal cells was not too short. Although the vertical extent of biomixing was surprisingly high (Δz ≥ 0.7) it might be of interest to study how it depends on population density. For comparison the population density of somewhat smaller mussels (L = 48 mm) was Npop ≈ 1260 ind.m-2with population filtration rate Fpop = 147 m3.d-1.m-2 in Lassen et al. [12] (Table 1) of flow past a mussel bed. If a similar mussel size and “natural” population density had been used in the present study, then the 147 m3.d-1.m-2 for the 0.25 m2 area of the aquarium would correspond to 102 l.min-1 and the half-life would have been very short: t½ = V/Fpop × ln2 = 175/102 × 0.693 = 1.2 min.
Next, although the time scales of experiments on the 3 species in Table 2 are similar the developing concentration profiles are quite different. For Nereis intestinalis the biomixing is weak and the profile has the characteristic form of a concentration boundary layer that slowly develops up into the overlying water [10]. For Ciona intestinalis the height of fully mixed layer develops after 1 h to 2 h and then remains constant [11] while its level decreases with time. For Mytilus edulis biomixing extends to the full height of the overlying water at most after 15 min after which the essentially uniform concentration decreases with time.
| Species | Npop (ind.m-2) | Fpop (m.h-1) | ΔMix (m) | D (×10-6 m2.s-1) | Reference |
|---|---|---|---|---|---|
| Nereis diversicolor | 120-186 | 0.054-0.088 | 0.01-0.015 | 0.3 | [10] |
| Ciona intestinalis | 233 | 0.28 | 0.2-0.3 | 150 | [11] |
| Mytilus edulis | 48 | 0.2-0.3 | ≥ 0.7 | 550 | Present study |
Table 2: Characteristics of biomixing experiments. Population density (Npop) and filtration rate (Fpop), extent of biomixing above animals (ΔMix), and estimated eddy diffusivity of mixing (D).
These differences may be interpreted as follows. In all experiments, the biomixing process with a distribution of eddy diffusivity D(z) is already established when at time t = 0 the depletion of the initially uniform concentration distribution begins. As algae are being consumed by the filter-feeders a concentration boundary layer develops upwards with an approximate penetration depth that increases as δ ≈ (D t)1/2, which is also a solution to Eqs. (1) and (2). Assuming the diffusivity to be constant over this layer for Nereis diversicolor (D = 0.3 × 10-6 m2.s-1 from Table 2, we find δ (20 min) ≈ 0.019 m, δ (60 min) ≈ 0.033 m and δ (180 min) ≈ 0.057 m, which are in reasonable agreement with measurements in Riisgård et al. [10] (Figure 3). For Ciona intestinalis (D = 150 × 10-6 m2.s-1, Table 2) at the first measured profile at t = 0.75 h [11] we obtain the estimate δ (0.75 h) ≈ 0.64 m which exceeds the value observed (≈ 0.20-0.40 m). But to match the numerical model to observations in Larsen and Riisgård [8] it was found that the eddy diffusivity had to decrease from the high value near the bottom (D = 150 × 10-6 m2.s-1) to a low value (D = 0.42 × 10-6 m2.s-1) over a short distance about 0.2 m above the bottom. Physically it is the decrease of effective biomixing that limits the penetration of the mixed layer. Finally for Mytilus edulis of the present study, the estimated penetration at the time of the first recorded profile at t = 15 min (Figure 4) becomes δ (15 min) = (150 × 10-6 × 15 × 60)1/2 ≈ 0.704 m which is the full height of the water column in the aquarium. This does not resolve the question to which height biomixing is limited. However, the strength of biomixing appears to be largely unchanged to a height of at least 0.7 m for the present large blue mussels at relatively low population density. This important but somewhat surprising result encourages execution of more biomixing studies imitating the present experimental approach, but using sufficiently high aquaria, various population densities, and mussels with various shell length.
The high strength of biomixing documented for Mytilus edulis in the present study suggests that biomixing may contribute to downmixing of phytoplankton not only in stagnant water but also in moderate benthic boundary layer flows past mussel beds, or flows past mussels growing on ropes in aquaculture systems.