Journal of Theoretical & Computational Science
Open Access
ISSN: 2376-130X
ISSN: 2376-130X
Research Article - (2014) Volume 1, Issue 1
Specific impulse is an important property of propellants, which are a kind of explosive (energetic materials) or explosive mixture. Based on some physical principles and mathematics, a formula for the specific impulse values of pure explosives has been derived. Inspection of the formula on the relative bases (relative to the specific impulse value of HMX) revealed that it is an upper bound as long as the molecular weight is less than ca. 276, thereafter, approximately equal or slightly deviates from the relative specific impulse values excerpted from the literature.
<Keywords: Specific impulse, Propellants, Explosive, Bounds, DFT calculations, Angle of detonation velocity
The specific impulse of an energetic material is the most important characteristic of the performance, thus it is the widely used property of propellants [1,2]. Due to the discharge of gaseous products formed, an energetic material develops a recoil force (thrust). The specific impulse, Is, is the integral of the thrust, per unit weight of material, over the time of combustion [2,3]. The specific impulse can be estimated by some computer codes [4,5]. It can be also predicted if one knows the detonation velocity (DCJ, Chapman-Jouguet) and density, by using the empirical formula of Keshavarz and Pouretedal which is in its original form estimates DCJ if Is value and density are known [6].
Propellants are energetic materials and differ from explosives with their low rates of combustion that will ideally burn at uniform rates after ignition without requiring atmospheric interaction [2]. Desirably, they should have no brisance effect. Propellants are usually admixture of various components, including an energetic oxidizer, a plasticizer to facilitate processing and a polymeric binder. Thus, the specific impulse value of such a propellant is that of the composite mixture. The specific impulse can be expressed as [1,7].
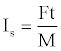 (1)
(1)
Where, F: thrust; t: time; M: weight of propellant. It is measured in kilo pounds-sec or Newton-sec per kilogram of propellant. It can be expressed also by the equation; [1]
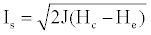 (2)
(2)
Where, J is mechanical heat equivalent; Hc: enthalpy of the reaction products in the rocket chamber (in kcal/kg) at chamber pressure and temperature; He: enthalpy of the reaction.
If the products at the rocket nozzle exit is in kcal/kg, then the Is becomes N.sec/kg.
On the other hand, the relation between the specific impulse Is and the temperature of the reaction gas in the rocket chamber is [1],
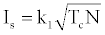 (3)
(3)
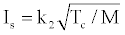 (4)
(4)
Where Tc: flame temperature in the chamber, N: number of moles per unit weight; M: average molecular weight of the flame gases; k1 and k2 are certain constants. The specific impulse value becomes high if the heat of reaction is high, which consequently produces a high flame temperature, and if the average molecular weight of the reaction products is low [8]. Various studies exist in the literature about the factors effective on the specific impulse [9-15].
In the present study, a different formulation for Is has been derived as a function of molecular weight and the angle of detonation. Another formula inter relates the specific impulse with the molecular weight, the total energy and the detonation velocity.
The elliptical and circular models have been developed for the detonation velocity of explosive materials [16,17]. The circular model is a simplified version of the elliptical one. Below theory relies on the circular model [17], in which the detonation velocity is expressed as (Figure 1),
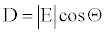 (5)
(5)
Where, the unit of D and E are so properly chosen that
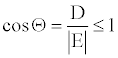 (6)
(6)
Where, E is the total energy of the molecule under consideration. From now on, the absolute value of E will be designated as just E
Figure 1 hereabouts
Construct E/D ratio.
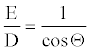 (7)
(7)
On the other hand, consider the general formula for work,
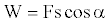 (8)
(8)
Where F is the force applied, s is the path covered and α is the angle between F and s (Figure 2). Now assume that an energetic material burns in time t, the energy propagates radially and produces radial recoil forces in all directions. The radial force Fi and force Fx along the x-axis has the relationship that
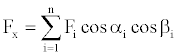 (9)
(9)
The summation in space is better expressed by integral,
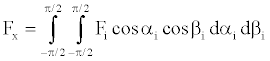 (10)
(10)
If the energy evenly distributed radially, then all Fi are equal to F’, then
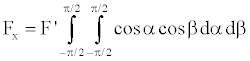 (11)
(11)
Then work, W, along path s in x-direction becomes
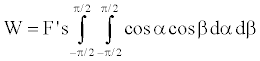 (12)
(12)
The double integration yields a numerical value say R. Hence the work,
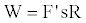 (13)
(13)
Then assume that certain fraction of the total energy is converted to available energy consumed to perform the work expressed by equation 14, i.e.
Figure 2 hereabouts
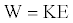 (14)
(14)
K is a conversion factor between the total energy and the available energy along certain direction. Since W is assumed to be a fraction of the total energy (E), then K ≤ 1. It should reflect the brisance in certain functional form.
On combining equations 13 and 14 one gets,
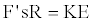 (15)
(15)
And solving for E,
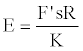 (16)
(16)
Inserting equation 16 and D=L/t (the definitive formula for the detonation velocity) into equation 7, it becomes
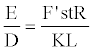 (17)
(17)
Where, s and L are the distances and t is the time for the detonation velocity measurement. Let L=ks, where k is proportionality constant. Then equation 17 becomes,
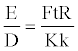 (18)
(18)
Since by definition Ft is equal to impulse I [1], then equation 18 can be written as
 (19)
(19)
Combining equations 7 and 19 we get,
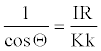 (20)
(20)
Solving for I,
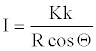 (21)
(21)
In the present study, after achieving the initial geometry optimizations by using MM2 method, followed by the semi-empirical PM3 self-consistent fields molecular orbital (SCF MO) method [18,19], at the restricted level [20,21], then STO, RHF and Density Functional Theory (DFT-UB3LYP) [22,23] type quantum chemical calculations have been consecutively performed for the geometry optimizations with 6-31G(d) basis set to obtain energetically the most favorable structures of the presently considered species. The exchange term of B3LYP consists of hybrid Hartree-Fock and local spin density (LSD) exchange functions with Becke’s gradient correlation to LSD exchange [23,24]. The correlation term of B3LYP consists of Vosko, Wilk, Nusair (VWN3) local correlation functional [25] and Lee, Yang, Parr (LYP) correlation functional [26].
For each set of calculations, vibrational analyses were done (using the same basis set employed in the corresponding geometry optimizations). The normal mode analysis for each structure yielded no imaginary frequencies for the 3N-6 vibrational degrees of freedom, where N is the number of atoms in the system. This indicates that the structure of each molecule corresponds to at least a local minimum on the potential energy surface. Furthermore, all the bond lengths were thoroughly searched, in order to find out whether any bond cleavage occurred during the geometry optimization process. Geometry optimizations and the vibrational analysis computations were performed by using the Spartan 06 package program [27].
Equation 21 needs to have another coefficient (c) for the reconciliation of the numerical result with the result in the conventional unit(s) of impulse. In terms of the specific impulse Is [1,2], equation 21 can be written as,
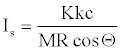 (22)
(22)
Where, M stands for molecular weight. Note that K depends on molecular structure. So, available energy defined in the theory part may be different from molecule to molecule, even though two explosives had the same total energy by coincidence. The meaning of “molecular structure” in connection with K should be dealt as comprising all the molecular properties, which contribute to explosiveness of the molecule under consideration, namely gross and fine topologies, bond energies, crystal forms (for solids), etc., if one wishes to correlate with experimental results of impulse. Since K ≤ 1 and M>>1, so Is values in reality should be less sensitive to variations in K than the values expected by equation 22 at the first sight.
Equation 22 in the light of above consideration turns into in equation 23 because K ≤ 1.
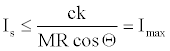 (23)
(23)
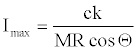 (24)
(24)
Equation 22 could be useful for the relative comparison of Is values if K value is found or estimated someway. Note that partial derivative of equation 22 with respect to K is,
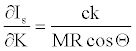 (25)
(25)
The right hand side of equation 25 is equal to Imax (equation 24). Then inserting equation 24 into equation 25,
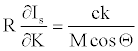 (26)
(26)
Let 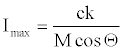 , then equation 26 becomes,
, then equation 26 becomes,
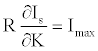 (27)
(27)
Note that R is a numerical constant. Table 1 shows M, Θ (in radian) and absolute values of c(M cosΘ)-1 for a series of explosives. The E/D ratio initially is in unit of au.sec.km-1. In the table the right hand side of in equation 23 is in N.sec.g-1. The conversion factor is 2625.52. Note that c(M cosΘ)-1 values presented in Table 1 cannot be directly compared with each other (equation 25 is a partial derivative, not a total derivative of Is with respect to the structural variable K), because each explosive supposed to have different K value which is neglected in equation 23 or equation 24. Moreover, c(M cosΘ)-1 term is actually Imax/k and k is not independent from structural influences. However, on the relative bases, such kind of errors may cancel out each other. Also, Imax defined by equation 26 cannot be certainly described as the lowest or highest upper bound because k might be greater or less than unity.
| Name | M(g) | Corrected total energy (au) | D (km/s)[28,29] | Q (rad) | 2625.52* (Mw cosΘ)−1 (N.sec/g) in Absolute value | Is Relative to HMX |
|---|---|---|---|---|---|---|
| DMNA | 90 | -339.5607 | 6.29 | 1.5893 | 1576.666 | 1.35 |
| EDNA | 150 | -599.3723 | 8.42 | 1.5848 | 1249.961 | 1.07 |
| MNA | 76 | -300.2773 | 6.7 | 1.5931 | 1549.035 | 1.33 |
| OCPX | 164 | -638.6573 | 7.28 | 1.5821 | 1416.319 | 1.21 |
| DMEDNA | 178 | -677.9375 | 6.42 | 1.5802 | 1568.571 | 1.34 |
| TNB | 213 | -845.6280 | 7.42 | 1.5795 | 1416.246 | 1.21 |
| 1,8-DNN | 218 | -794.7184 | 5.38 | 1.5775 | 1796.591 | 1.54 |
| 1,5-DNN | 218 | -794.7266 | 5.52 | 1.5777 | 1744.545 | 1.49 |
| TENN | 308 | -1203.6771 | 7.3 | 1.5768 | 1419.875 | 1.22 |
| TNT | 227 | -884.9094 | 7.02 | 1.5787 | 1463.407 | 1.25 |
| PAM | 228 | -900.9806 | 7.5 | 1.5791 | 1386.804 | 1.19 |
| TNN | 263 | -999.2030 | 6.27 | 1.5770 | 1609.213 | 1.38 |
| PA | 229 | -920.8343 | 7.57 | 1.5790 | 1397.579 | 1.20 |
| DPM | 438 | -1729.3358 | 7.29 | 1.5750 | 1425.98 | 1.22 |
| DPE | 452 | -1768.6195 | 7.2 | 1.5748 | 1450.84 | 1.24 |
| DIGEN | 74 | -299.0642 | 8.12 | 1.5979 | 1309.208 | 1.12 |
| HNS | 450 | -1767.4194 | 7.27 | 1.5749 | 1421.776 | 1.22 |
| Tetragen | 148 | -598.1450 | 8.46 | 1.5849 | 1257.87 | 1.08 |
| CPX | 162 | -637.4639 | 7.76 | 1.5829 | 1339.041 | 1.15 |
| DNDC | 176 | -676.7560 | 6.75 | 1.5807 | 1506.307 | 1.29 |
| RDX | 222 | -897.2650 | 8.89 | 1.5807 | 1194.189 | 1.02 |
| TEX | 274 | -1052.5950 | 8.47 | 1.5788 | 1197.237 | 1.03 |
| HNIW | 438 | -1790.9610 | 9.62 | 1.5761 | 1130.229 | 0.97 |
| HMX | 296 | -1196.3540 | 9.13 | 1.5784 | 1166.553 | 1.00 |
| TNAD | 296 | -1273.7220 | 8.52 | 1.5774 | 1343.202 | 1.15 |
| MDN | 121 | -504.7299 | 9.05 | 1.5887 | 1212.023 | 1.04 |
Table 1: Some data for the explosives considered presently.
Table 1 hereabouts
However, equation 22 and equation 23 indicate that the cosine value of “angle of detonation” [16,17] inversely influence the impulse value. Since, cosΘ ≤1 (or, 1/ cosΘ ≥1), it is the main contributor of Is (note that the structure dependent variables K and 1/M are less than unity). However, cos Θ values vary in a very small range for different explosives (Table 1 for Θ values). By inserting equation 6 into equation 22 it can be written as,
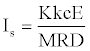 (28)
(28)
Since E of organic molecules generally increase with molecular weight, in equation 28, E/M ratio could be certain function of M, where the exponent of M might be different from -1 (as in the case of equation 4). The E/M ratio of most of the explosives falls into the range of 3.6-4.2 within the same level of calculations (UB3LYP/6- 31G(d)) [17,30]. According to equation 28, as E increases in absolute value or D decreases then the impulse value increases. So, energetic material having low brisance (deflagration preferred) will be a better propellant. The E/M ratio embedded in equation 28 is the total energy per gram of material, and as it increases, the specific impulse value increases. As long as cos Θ and K values in equation 22 are close to each other, then Is values of two or more propellants will be inversely proportional with their molecular weights. This conclusion has been supported by the calculations of Politzer et al. [31], who used equation 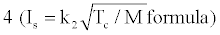 .
.
On the other hand, starting from equation 22, for two explosives indicated by sub-indices 1 and 2, the ratio of Is values is,
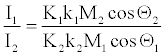 (29)
(29)
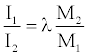 (30)
(30)
Where λ is,
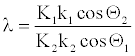 (31)
(31)
The ratio I1/I2 is the relative specific impulse value for explosive 1 relative to specific impulse value of 2.
Note that λ = 1 case is an ideal one. However, for structurally similar compounds, the structural factors K1 and K2 might be comparable. Also, cos Θ values vary in a very narrow range, and k values are related to respective detonation velocities. Thus, for two structurally similar explosives having comparable detonation velocities, λ might be close to unity.
Figure 3 shows variation of relative calculated specific impulse values (Icalc1) with molecular weights (using equation 30 with λ = 1 and molecular weight of HMX as M1) and Icalc2 values (Icalc2 values have been taken from ref. 2 which are relative to HMX value again, and had been calculated by means of equation 3) for a series of explosive materials. From Figure 3, it is evident that Icalc1 values decreases with increasing molecular weight on the arm of a hyperbola. It also indicates that Icalc1 values are greater than Icalc2 values in most of the cases, and asymptotically approaches the Icalc2 values plot. Inspection of Table 2 reveals that Icalc1 slightly below Icalc2 as molecular weights increases above 276 g/mole. On the other hand, inspection of the structures depicted in Figure 4 indicates that there is no structural dependence (except M) between the decreasing tendency of Icalc1 and the type of compounds, and/or number of such groups N-NO2, NFx or C-NO2, etc. The importance of structural factor K and E/M ratio become obvious if one considers groups of structures 10,11,12; 17,18; 30,31, and 34,35. In some cases, Irel values are the same in other cases, different even though M values are the same.
| Data no | M | Imax | Irel [31] |
|---|---|---|---|
| 1* | 61.00 | 4.85 | 1.15 |
| 2 | 76.03 | 3.89 | 1.25 |
| 3 | 124.05 | 2.39 | 1.22 |
| 4 | 140.05 | 2.11 | 1.09 |
| 5 | 144.05 | 2.06 | 1.14 |
| 6 | 152.06 | 1.95 | 1.13 |
| 7 | 152.06 | 1.95 | 1.16 |
| 8 | 158.07 | 1.87 | 1.14 |
| 9 | 158.07 | 1.87 | 1.15 |
| 10 | 158.07 | 1.87 | 1.17 |
| 11 | 158.07 | 1.87 | 1.17 |
| 12 | 158.07 | 1.87 | 1.18 |
| 13 | 172.10 | 1.72 | 1.10 |
| 14 | 186.09 | 1.59 | 1.18 |
| 15 | 186.09 | 1.59 | 1.20 |
| 16 | 192.07 | 1.54 | 1.12 |
| 17 | 216.05 | 1.37 | 1.05 |
| 18 | 216.07 | 1.37 | 1.13 |
| 19 | 224.08 | 1.32 | 1.04 |
| 20* | 227.10 | 1.30 | 0.97 |
| 21 | 228.12 | 1.29 | 1.07 |
| 22* | 243.00 | 1.22 | 0.82 |
| 23 | 248.09 | 1.19 | 1.10 |
| 24* | 258.10 | 1.15 | 0.76 |
| 25 | 260.12 | 1.14 | 1.02 |
| 26 | 264.10 | 1.12 | 1.02 |
| 27 | 276.11 | 1.07 | 1.12 |
| 28 | 278.12 | 1.06 | 1.08 |
| 29 | 284.14 | 1.04 | 1.05 |
| 30* | 287.10 | 1.03 | 0.87 |
| 31 | 287.10 | 1.03 | 1.12 |
| 32 | 288.09 | 1.03 | 1.15 |
| 33 | 296.15 | 1.00 | 1.00 |
| 34 | 304.12 | 0.97 | 1.14 |
| 35 | 304.12 | 0.97 | 1.14 |
| 36* | 316.10 | 0.94 | 0.97 |
*Impulse values used for the calculation of Irel from ref. 6, others from ref. 31. See Figure 4 for some of the structures. Imax values are relative to the value of HMX.
Table 2: Some data for the explosives presently considered.
The present treatise shows that the specific impulse of an explosive has contributions directly from the total energy of the molecule, but inversely from the molecular weight and the detonation velocity. These are explicit contributions. However, the structural factors, altogether represented by K, also contribute obviously in to the specific impulse value, but the direction of its effect (increasing or decreasing) is highly structure specific. The overall contribution of factor K, due to its structural dependence, makes equation 28 acts as an upper bound, which is far off from the literature values of the specific impulses for low molecular weight explosives. However, as the molecular weight increases, its contribution (in the form of K/M) in equation 28 decreases, hence the equation predicts Is values much better.