Journal of Aeronautics & Aerospace Engineering
Open Access
ISSN: 2168-9792
ISSN: 2168-9792
Research Article - (2014) Volume 3, Issue 1
The effect of various offaxis angles and lamina material properties on the axial and transverse modulus of the orthotropic lamina under off-axis loading is studied. Also, the stress distribution of the orthotropic composite plate containing a circular cutout with normal pressure distributed uniformly along the opening edge is investigated. Through the generalized Hooke’s law and plane stress condition, a dimensionless analysis is used to evaluate the influence of various elastic moduli E1, E2, G12 and ν12 on the axial and transverse modulus of the orthotropic lamina under various off-axis loadings. Moreover, based on the generalized Hooke’s law, the generalized plane stress and the complex variable method, a dimensionless analysis is used to evaluate the influence of various elastic moduli E1, E2, G12 and ν12 on the stress distribution along the boundary of the circular cutout of the orthotropic plate with normal pressure distributed uniformly along the opening edge. The results obtained from this dimensionless analysis provide a set of general design guidelines for structural laminates with high precision requirements in the engineering applications.
<Keywords: Lamina; Axial and transverse modulus; Orthotropic plate; Complex variable; Offaxis angle; Stress distribution; Composite materials
Composite materials consist of various fibrous reinforcements coupled with a compatible matrix to achieve superior structural performance. The selection of composite materials for specific applications is generally determined by the physical and mechanical properties of the materials, evaluated for both function and fabrication [1]. The axial and transverse modulus of a composite laminate is an important physical parameter in the application and testing of composite materials. Knowledge of stress distributions in anisotropic materials is very important for proper use of these new high-performance materials in structural applications [2].
Schulgasser and Page [3] considered the importance of the transverse or non-axial fiber properties in determining the in-plane elastic behavior of a paper sheet. Scott [4] defined a new modulus of elasticity to be the ratio of an equibiaxial stress to the relative area change of the planes in which the stress acts. This area modulus of elasticity is intermediate in properties between Young’s modulus and the bulk modulus. Spencer [5] described a simple method which used axial and torsional vibration resonance for the measurement of Young’s modulus, E, and shear modulus, G, of shafts. Zheng and Zhu [6] investigated the effect of an applied electric field on Young’s modulus of nanowires. Upadhyay and Lyons [7] calculated effective elastic constants of threephase composite with degraded interphase coating for the graphite/ epoxy composite system.
Kuwamura [8] analyzed the stresses around the circular hole by means of Ikeda’s formula in consideration of orthotropic elasticity of the woods, which revealed that the stresses distribution around the circular hole is nearly equal to that of an isotropic plate. Selivanov [9] studied the time variation in the stresses around an elliptic hole in a composite plate. Kumar and Rao [10] presented an approximate solution in the form of a polynomial for the normal stress distribution adjacent to a class of optimum holes in symmetrically laminated infinite composite plates under uniaxial loading. Giare and Shabahang [11] used a finite element analysis to calculate the stress distribution around a hole in a finite isotropic plate reinforced by composite materials. Tsai et al. [12] developed a novel procedure for predicting the notched strengths of composite plates each with a circular hole and the stress distribution of the circular cutout is obtained by a finite element analysis.
A dimensionless analysis model for evaluation of axial and transverse modulus
Based on the generalized Hooke’s law and the related plane stress equations in the global coordinates, axial and transverse modulus, Ex and Ey, has been derived [13-18]. The transformed plane stress constitutive equations can be inverted to give [14-18].
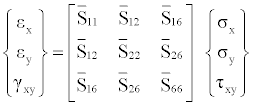 (1)
(1)
The unidirectional off-axis lamina under the loading σx ≠ 0 with σy= τxy=0, as depicted in Figure 1, the axial modulus, Ex, can be written as [14-18].
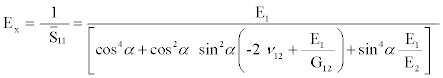 (2)
(2)
Similarly, the transverse modulus, Ey, can be written as [14-18]
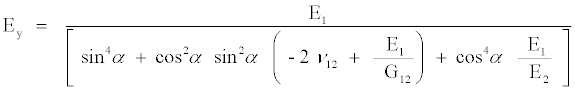 (3)
(3)
Consider the unidirectional off-axis lamina under the loading σx≠0 and the off-axis angle α varying from -90° to 90°. For a dimensionless analysis, three lamina material constants E1, E2 and G12 are represented by two dimensionless ratios E2/E1 and G12/E1. Totally, the lamina material has three parameters E2/E1, G12/E1 and ν12. For an unidirectional off-axis lamina with different values of E2/E1, G12/E1, ν12 and α, the axial and transverse modulus of the lamina under the off-axis loading will vary and provide different values.
Various cases of different combinations of three material parameters are considered in this study. In general case, the ranges of E2/E1 and G12/ E1 are between zero and one, the ranges of ν12 are between 0 and 0.6. For a lamina with given material properties E2/E1, G12/E1 and ν12 as well as the off-axis angle α, the axial and transverse modulus in the lamina under off-axis loading can be evaluated.
Tangential stresses on the boundary of the circular opening
The stress-strain distribution of an infinite anisotropic plate containing a through-the-thickness cutout has been derived using a complex variable method [19-21]. For an orthotropic plate subjected to normal pressure q distributed uniformly along the opening edge as shown in Figure 2. The normal stress component σθ for an element tangential to the opening is [20]
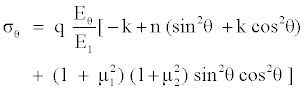 (4)
(4)
where
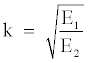 (5)
(5)
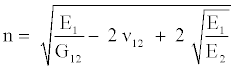 (6)
(6)
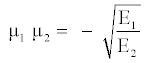 (7)
(7)
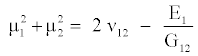 (8)
(8)
The θ is the polar angle measured from the x-axis; Eθ is the Young’s modulus tension (compression) in the direction tangent to the opening contour, which is related to elastic constants in the principal directions by the formula [20].
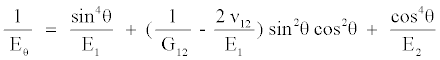 (9)
(9)
For an isotropic plate [20]
σθ=q (10)
A dimensionless analysis model for evaluation of the normal stress σθ
Consider the orthotropic plate with a circular hole subjected to normal pressure q distributed uniformly along the opening edge. For a dimensionless analysis, three lamina material constants E1, E2 and G12 are represented by two dimensionless ratios E2/E1 and G12/E1. Totally, the lamina material has three parameters E2/E1, G12/E1 and ν12. For a unidirectional lamina with different values of E2/E1, G12/E1 and ν12, the normal stress component σθ of the orthotropic plate under normal pressure q distributed uniformly along the opening edge will vary and provide different values.
Various cases of different combinations of three material parameters are considered in this study. In general case, the ranges of E2/E1 and G12/ E1 are between zero and one, the ranges of ν12 are between 0 and 0.6. For a lamina with given material properties E2/E1, G12/E1 and ν12, the normal stress component σθ of the orthotropic plate under normal pressure q distributed uniformly along the opening edge can be evaluated.
Since the variation of the axial modulus Ex is bilateral symmetry to the off-axis angle α=0, the variation of the axial modulus Ex is considered only in the range of 0° ≤ α ≤ 90°. Also, the curves of transverse modulus Ey are identical to those for Ex, but shifted 90°. Thus, only the variation of the axial modulus Ex is considered.
Given E1=204GPa, G12/E1=0.2 and ν12=0.2, the variations of the axial modulus Ex with off-axis angle α and different values of E2/E1 are shown in Figure 3. For different off-axis angle α and various values of E2/E1 from 0.2 to 0.4, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum values at α=90° as shown in Figure 3. But for E2/E1=0.6, with different off-axis angle α, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum value at α=60° and then increases to a large value at α=90°as shown in Figure 3. As for E2/E1=0.8 with different off-axis angle α, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum value at α=45° and then increases to a large value at α=90° as shown in Figure 3. Finally, for E2/E1=1.0, with different off-axis angle α, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum value at α=45° and then increases to the maximum value at α=90° as shown in Figure 3.
Given E1=204GPa, E2/E1=0.4 and ν12=0.2, the variations of axial modulus Ex with off-axis angle α and different values of G12/E1 are shown in Figure 4. For different off-axis angle α and various values of G12/E1 from 0.2 to 0.4, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum values at α=90° as shown in Figure 4. As for the changed values of G12/E1 from 0.6 to 1.0, with different off-axis angle α, the axial modulus Ex varies first from a large value at α=0° then increases to the maximum value at α=30° and then decreases to the minimum value at α=90° as shown in Figure 4.
Given E1=204GPa, E2/E1=0.6 and G12/E1=0.4, the variations of the axial modulus Ex with off-axis angle α and different values of ν12 are shown in Figure 5. With different off-axis angle α and ν12=0.2, the axial modulus Ex varies first from the maximum value at α=0° then decreases to the minimum value at α=90° as shown in Figure 5. As for the changed values of ν12 from 0.4 to 0.6, with different off-axis angle α, the axial modulus Ex varies first from a large value at α=0° then increases to the maximum value at α=30° and then decreases to the minimum value at α=90° as shown in Figure 5.
In the Figures 6-8, the bold solid line represents the circular hole and the bold dotted line shows the stress distribution σθ in an isotropic plate subjected to identical load as in an orthotropic plate. Since the stress distribution for an orthotropic plate is symmetrical with respect to the opening center, the variation of the stress distribution σθ is considered only in the range of 0° ≤ θ ≤ 180° for an orthotropic plate. In an isotropic plate given q=100 MPa, then calculated from Equation (10), the constant stress σθ is 100 Mpa.
In Figure 6 given q=100 MPa, E1=204 GPa, E2/E1=0.6 and G12/ E1=0.4, the variation of the stress σθ with respect to the polar angle θ and ν12 is the following:
With ν12=0.2, 0.4, and 0.6, the minimum corresponding stresses σθ are 87.28 Mpa, 77.83 Mpa, and 67.93 Mpa at θ=90° respectively, and the maximum stresses σθ are 111.62 Mpa, 121.17 Mpa, and 132.14 Mpa at θ=50° and θ=130° respectively. Also, the stress concentration factors are Sc=1.12, 1.21, and 1.32 respectively, for orthotropic case. Figure 6 shows that within the ranges of the polar angle 0° ≤ θ ≤ 20°, 70° ≤ θ ≤ 110° and 160° ≤ θ ≤ 180°, the stress σθ decreases along with the increased values of ν12 respectively. But, in the ranges of the polar angle 30° ≤ θ ≤ 60° and 120° ≤ θ ≤ 150°, the stress σθ increases along with the increased values of ν12.
In Figure 7 given q=100 MPa, E1=204 GPa, E2/E1=0.6 and ν12=0.4, the variation of the stress σθ with respect to the polar angle θ and G12/ E1 is following:
For G12/E1=0.2, the minimum corresponding stresses σθ are 76.16 Mpa at θ=50° as well as θ=130°, and for G12/E1=0.4, 0.6, 0.8 and 1.0, the minimum corresponding stresses σθ are 77.83 Mpa, 56.61 Mpa, 45.03 Mpa and 37.69 Mpa at θ=90° respectively. With G12/E1=0.2, the maximum stresses σθ are 124.26 Mpa at θ=0° as well as θ=180°, and with G12/E1=0.4, 0.6, 0.8 and 1.0, the maximum stresses σθ are 121.17 Mpa, 146.09 Mpa, 162.21 Mpa and 173.54 Mpa at θ=50° as well as θ=130° respectively. Also, the stress concentration factors are Sc=1.24, 1.21, 1.46, 1.62, and 1.73 respectively, for orthotropic case. Figure 7 indicates that within the ranges of the polar angle 0° ≤ θ ≤ 20°, 70° ≤ θ ≤ 110° and 160° ≤ θ ≤ 180°, the stress σθ decreases along with the increased values of G12/E1 respectively. But, within the ranges of the polar angle 30° ≤ θ ≤ 60° and 120° ≤ θ ≤ 150°, the stress σθ increases along with the increased values of G12/E1.
In Figure 8 given q=100 MPa, E1=204 GPa, G12/E1=0.6 and ν12= 0.4, the variation of the stress σθ with respect to the polar angle θ and E2/E1 is following:
With E2/E1=0.2, 0.4, 0.6, 0.8 and 1.0, the minimum corresponding stresses σθ are 7.45 Mpa, 42.61 Mpa, 56.61 Mpa, 64.34 Mpa and 69.31 Mpa at θ=90° respectively, and the maximum stresses σθ are 177.49 Mpa, 157.60 Mpa, 146.09 Mpa, 138.66 Mpa and 133.47 Mpa at θ=50° and θ=130° respectively. Moreover, for E2/E1=1.0, the minimum stresses σθ occurred at θ=0° and θ=180° and the maximum stresses σθ occurred at θ=40° and θ=140° as well. Also, the stress concentration factors are Sc=1.77, 1.58, 1.46, 1.39, and 1.33 respectively, for orthotropic case. Figure 8 shows that within the ranges of the polar angle 0° ≤ θ ≤ 30°, 80° ≤ θ ≤ 100° and 150° ≤ θ ≤ 180°, the stress σθ increases along with the increased values of E2/E1 respectively. But, in the ranges of the polar angle 40° ≤ θ ≤ 60° and 120° ≤ θ ≤ 140°, the stress σθ decreases along with the increased values of E2/E1. As for the polar angles both θ=70° and θ=110°, with the various values of E2/E1 from 0.2 to 0.6 the stress σθ decreases along with the increased values of E2/E1, but with the various values of E2/E1 from 0.6 to 1.0 the stress σθ increases along with the increased values of E2/E1.
The effect of various offaxis angles and lamina material properties on the axial and transverse modulus of the orthotropic lamina under off-axis loading is studied. Also, the stress distribution of the orthotropic composite plate containing a circular cutout under normal pressure distributed uniformly along the opening edge is investigated.
First remark, given the fixed off-axis angle α and other fixed material parameters Figure 3 shows that the values of the lamina axial modulus Ex increase along with the increase values of E2/E1 except at α=0°.
Second remark, given the fixed off-axis angle α and other fixed material parameters Figure 4 shows that the values of the lamina axial modulus Ex increase along with the increase of the values of G12/E1 except for α=0° and α=90°.
Third remark, given the fixed off-axis angle α and other fixed material parameters, Figure 5 indicates that the values of the lamina axial modulus Ex increase along with the increase of the values of ν12 except at α=0°and α=90°.
Fourth remark, given other fixed material parameters Figures 6 and 8 indicates that within the ranges of the polar angle 0° ≤ θ ≤ 90°, the stress σθ varies first from a small value at θ=0° then increases to the maximum value at θ=50° and then decreases to the minimum value at θ=90°. But within the ranges of the polar angle 90° ≤ θ ≤ 180°, the stress σθ varies first from the minimum value at θ=90° then increases to the maximum value at θ=130° and then decreases to a small value at θ=180° as shown in Figures 6 and 8.
Fifth remark, given other fixed material parameters Figure 7 indicates that for the value of G12/E1=0.2, within the range of the polar angles 0° ≤ θ ≤ 90°, the stress σθ varies first from a large value at θ=0° then decreases to the minimum value at θ=50° and then increases to the maximum value at θ=90°. But within the ranges of the polar angle 90° ≤ θ ≤ 180°, the stress σθ varies first from the maximum value at θ=90° then decreases to the minimum value at θ=130° and then increases to a large value at θ=180° as shown in Figure 7. As for the values of 0.4 ≤ G12/ E1 ≤ 1.0, within the range of the polar angles 0° ≤ θ ≤ 90°, the stress σθ varies first from a small value at θ=0° then increases to the maximum value at θ=50° and then decreases to the minimum value at θ=90°. But within the ranges of the polar angle 90° ≤ θ ≤ 180°, the stress σθ varies first from the minimum value at θ=90° then increases to the maximum value at θ=130° and then decreases to a small value at θ=180° as shown in Figure 7.
The results obtained from this dimensionless analysis provide a set of general design guidelines for structural laminates with high precision requirements in the engineering applications.