Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 2
There exists literature that explores the linkages between yield curve, economic activity and monetary policy. Although empirical work has been done to show the significance of the slope of yield curve in predicting economic slowdowns, it has predominantly been for the developed markets of the US, Europe and so on. This paper explores the predictive power of the slope of yield curve in forecasting economic slowdowns in India through the use of wavelet based filtering. We develop a new approach using duration models to enable the construction of real time forecasting of recession probabilities.
<The slope of the yield curve, defined as the spread between the long and short term interest rates, factors in it the future expectation of the interest rate scenario of the economy and has for long been used as a leading indicator in predicting economic slowdowns through the use of index of industrial production, real and nominal GDP growth and so on. This relationship has been well tested across time and geographies from periods dating back to the mid-nineties. In this paper we fit a duration model to estimate the conditional probability of an economic recession using the slope of the yield curve as a predictor. We focus on computing the conditional probability of a recession rather than trying to quantify the probability of an oncoming recession in general. We believe this is a useful approach and should be of relevance to policy makers as well as market participants. The slope of the yield curve as mentioned in this paper is defined as the spread between the yields of the ten-year government bond and three month (91 day) government bill as traded in the secondary market. We use government debt as they are not subject to credit risk premiums. This slope of the yield curve has been shown to have statistical significance in predicting future real economic activity for many countries. This relationship has been a stable one with particularly strong results obtained for Europe and the USA [1]. Many explanations have been cited for the yield curve slope’s predictability of economic slowdowns. As explained in [2] the slope of the yield curve builds in it the expectations of future inflation as well as the real interest rates. The spread can be seen as the forward interest rate applicable from three months to ten years into the future. Thus, a rise in the short term interest rate leads to flattening of the yield curve which may be seen as sign of monetary tightening in the economy. Mishkin in [3] and [4] shows how the spread between the long and short end of the interest rate curve can be decomposed into expected real interest rate and expected future inflation. The expected real interest rate can be used as a proxy for the future monetary policy, which in turn can be used to predict the future real growth in the economy. Also, monetary policies are believed to be reactive to future real inflation and thus a yield curve finds importance in predicting economic slowdowns over the forth-coming quarters. Most pundits of the literature have found the slope of the yield curve to be an effective predictor of recessions four to six quarters in advance. [5]. This relationship has been shown to exist even in an Indian context. Kanagasabapathy and Goyal [6] have used the yield curve slope as a leading indicator in predicting economic activity modeled using Industrial production index. They find the yield curve slope to predict a slowdown two to three quarters in advance. Golaka Nath have also made similar observations in their paper [7] wherein they find significant predictive power of the yield curve in predicting future industrial production growth four quarters in advance. In this paper, we use the yield curve to estimate the conditional probability of an economic slowdown in India. We model economic slowdowns using quarterly growth rate in real GDP and inflation. In order to investigate the effectiveness of the relationship over varied time horizons and thereby try to narrow down to a single period over which the relationship exists most strongly, we use wavelet based filtering for both the yield curve as well as the real GDP growth rate. We fit the filtered data series to a duration model to estimate conditional probability of a forth-coming economic slowdown.
Data and methodology
As mentioned in the sections above, we model economic activity using Real Gross Domestic Product (GDP). Real GDP data has been taken from Economics and Political Weekly Research Foundation (EPW Research Foundation) for the period of March 1971 to December 2012. We use quarterly data numbers for the purpose of our study. For modeling inflation, we use the Wholesale Price Index or the WPI from EPW Research Foundation adjusted for base changes. Starting from March 1971, we take monthly dump of each of the four WPI Price series: WPI (Base 1970-71=100), WPI (Base 1981-82=100), WPI (Base 1993-94=100) and WPI (Base 2004-05=100). We then obtain a single series by splicing the individual series adjusted to base of 1971. This is then converted into a quarterly series and used as a proxy for inflation. For computing the slope of the yield curve, we use yields of ten-year government bond and three-month (91 day) government bill as traded in secondary markets. This data is obtained using Thomson Reuters DataStream Professional package. Quarterly ten-year government bond rate is obtained using series INBD10Y while the three monthly Treasury bill is obtainied using INGBILL3 series. Difference between these two series is the yield spread. Post-independence era for the Indian economy was influenced by exploitative leaders and their exposure to socialism. The Indian currency was tightly controlled and pegged to the value basket of currencies of major trade partners. Policy makers induced protectionist policies with nationalization of major industries accompanied by elaborate licensing and a highly red taped regulatory environment to do business, commonly referred to as the Licenses Raj. The balance of payment crisis of 1991 almost led the country to default following which Indian currency was devalued, and an IMF bailout was soughed out for by pledging around sixty seven tons of gold as a part of the deal. Most economic reforms were forced upon India as a part of this bailout which led to the opening up of the economy, a market determined, free float currency, abolishment of License Raj so on and so forth. It is due to this economic liberalization that we choose the period of this study post 1994 as the regulatory environment, the currency, and policy decisions took a radical shift from a more socialistic economy to the current capitalistic one. For the US, National Bureau of Economic Research (NBER) derives the recession dates from the cyclical peaks and troughs of the economy. These dates are then used to calculate a monthly economic recession indicator with every month between a peak and following through (month of trough included, peak excluded) recorded as a recession. Similarly, NBER issues quarterly dates that are used to come up with quarterly recession indicator series. Although there have been arguments against this method of NBER, yet, it is still the most widely used recession classification for any US based research. In this paper we explore the relationship of the slope of the yield curve to predict a conditional probability for an economic slowdown in the Indian economy. In India, we do not have a formal body recording a recession and hence we choose to model economic activity by defining a measure:

RGDP is defined as the incremental growth in Real GDP adjusted for change in headline inflation as measured by WPI computed on a year on year basis at a quarterly frequency. Based on the measure thus defined, we classify the economy into two states:
a) Economic Expansion – This is defined as a state when the measure RGDP as defined above is positive.
b) Economic Slowdowns – this is defined as a state when the measure RGDP as defined above is negative.
While most of the available literature on Indian economy models future economic activity using Index of Industrial Production or the IIP we choose to use the Gross Domestic Product or GDP for our study. In India, the agriculture and service industries have significant contributions to economic growth and hence must be included in modeling future economic activity. As per [8] contributions as percentage of GDP have been as: agriculture: 17.4%, industry: 26.1% services: 56.5% (2012 estimated.) It is for this reason we believe IIP would be an incomplete barometer of economic activity of the country and thus we choose to model economic activity using GDP. Unlike developed markets, India is an emerging market and hence inflation plays a significant role in economic growth and this needs to be accounted for [9]. Developing economies almost always exhibit a positive growth rate when reviewed in terms of growth in real GDP. Continued economic expansion (higher growth rates in Real GDP over time) will be sustainable only if this growth is organic and greater than growth rate in inflation for the period under review. It is for this reason we change our scope from growth in Real GDP to incremental growth in Real GDP after accounting for headline inflation in a given period. According to the theory of expectation hypothesis, interest rate expectations have built in them expectations related to future real demand for credit and future inflation. A rise in the short-term interest rates as caused by monetary tightening leads to a slowdown in future economic activity resulting in lower expected inflation. This tends to decline the current long-term interest rates leading to flattening of the yield curve. A formal model with these properties is presented in [9]. Majority of the available literature on yield curves has been targeted towards the use of the level of yield curve to quantify future economic growth or to use the steepness of the yield curve in estimating the probability of recession. Formal statistical models like linear regressions and nonlinear equations have been used to quantify the sensitivity of future growth to changes in the term structure of interest rates. When the objective has been to estimate the probability of a recession, binary equations of probit and logit have been commonly used. Our analysis differs in two important aspects from the studies done so far. Firstly, we focus on directing our research to help policy makers take informed decisions while framing the monetary policy for the country. It is well documented in literature across different countries that inflation and growth have a non-linear relationship. For India, it is observed that there exists statistically significant negative effect of inflation on longterm growth with this effect being more predominant during high inflationary regimes. Nonetheless, it is critical to understand the time horizon over which inflation and growth significantly affect each other. For this purpose we introduce wavelet transformation on both the yield curve and growth rate in real GDP to extract the relationship between growth and inflation over varied time horizons as measured by the scale parameter of wavelet transformations. Secondly, rather than quantifying the future growth rate in real GDP, we focus on using the slope of the yield curve to compute a conditional probability of a future slowdown in the economic activity using the measure RGDP as defined above. This we believe should be of interest to market participants as it helps them prepare better for a forthcoming slowdown. For this purpose we use duration models with the economy modeled into two transient states and lagged yield curve as a predictor. Expected future short-term rates play a crucial role in driving current long-term interest rates. A tightening monetary policy implies an increase in current short-term rates and is intended to reduce inflationary pressures in the economy. Subsequent monetary easing follows only after these pressures subside. It is for this reason that current long-term interest rates tend to increase with monetary tightening but not as much as the short term rates due to expectation of future monetary easing, thereby flattening the yield curve. Monetary policy, though not the only, but is an important determinant of the predictive power of the yield curve. High frequency changes in the yield curve may result from temporary demand supply imbalances in the treasury markets and hence may not truly be reflective of changes in future real growth or future inflation. It is because of these reasons that we focus on studying the longterm effects of yield curve changes on future long term growth of the economy. We achieve this by using wavelet based filtering on the yield curve as well as the real GDP growth rate.
Wavelet theory
A time series signal when measured at a fixed time, gives us a precise value for the amplitude at that time, telling us nothing about the frequency spectrum of the signal. Time series analysis for trends, cycles, seasonality noise etc. requires the transformation of time series data into frequency domain. Traditionally this has been done using the Fourier Transform. However Fourier transforms have their own limitations to analyze signals whose characteristics vary with time. First, its underlying assumption of stationarity of the analyzing signal makes it unsuitable to be applied to economic indicators that are often subject to regime shifts, jumps, volatility clustering and so on and so forth. Second, the Fourier coefficients have only frequency dependence and hence cannot be used to perform temporal analysis. While economists have always argued for policy actions to be forward looking the period over which the dynamics of policy outcomes most closely relate to inflation and interest rate is of supreme importance and thus must be investigated. Through our analysis we attempt to answer this question and hence we choose to study the relationship between slope of yield curve and economic activity at varied time intervals to find which one is the most well defined one. The classical Fourier transform helps us precisely identify the frequency components of a signal but gives us no information on when in time do these occur. This is the limiting case of what is known as the Heisenberg Uncertainty Principle, one version of which states that frequency and time both cannot be made arbitrarily small. The wavelet transform helps us overcome these limitations with each wavelet measurement (the wavelet transform corresponding to a fixed parameter) telling us something about the temporal extent of the signal, as well as something about the frequency spectrum of the signal. They have their advantages over the traditional Fourier transform in that wavelet coefficient provide a time-frequency representation of time series signal telling you not only the frequencies contained in the signal but also where in time are they oriented. The signal to be analyzed is multiplied by a wavelet function, the width of which changes with each spectral component.
An analyzing function Ѱ(t) is classified as a wavelet if it satisfies the following mathematical properties:
1. A wavelet must have finite energy
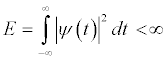
2. If Ѱ(f) is the Fourier Transform of the wavelet Ѱ(t), then following condition must hold.
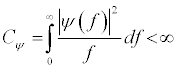
This implies that wavelets have no zero frequency component (Ѱ(0) = 0), meaning the mean of the wavelet Ѱ(t) must equal zero. This condition is called the admissibility constant.
3. For complex wavelets the Fourier transform Ѱ(f) must be both real and must vanish at negative frequencies.
It is these conditions that decide the shape of the wavelet function.
The basic theme behind wavelet transforms is to represent an arbitrary function in time f(t) as a superposition of a set of wavelet functions. These wavelet functions are also known as the basis functions or baby wavelets and are obtained from a single prototype wavelet called mother wavelet, by dilatations or contractions (scaling) and translations (shift).
A mother wavelet is defined as a function Ѱ(t) on the real axis and satisfying:
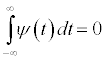
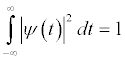
The wavelet basis functions are then generated from this single mother wavelet Ѱ(t) through scaling and translation:
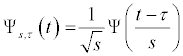
where:
s: is the scale factor
τ: is the translation factor and
√s: for energy normalization across different scales
The wavelet transform which is then a function of scale s and translation τ is obtained by taking the projections of the original function f(t) onto the bases functions defined as:
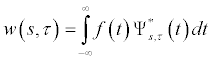
A low value of the scale s corresponds to a compressed wavelet and is useful in extracting the high frequency components of time domain signal f(t). Similarly, a high value of s corresponds to a stretched wavelet and is useful in extracting low frequency components of f(t).
The discrete wavelet transform is a parsimonious version of the above mentioned continuous time wavelet transforms where scales s and translations τ are chosen such that:
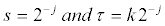
where j, k are integers representing the sets of discrete translations and discrete dilatations with
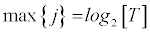
T being the length of the original signal f(t)
Discrete wavelet transform is implemented by passing the time domain signal through a series of filter banks where they are decomposed into “approximations” and “detail” components.
The approximations are the low frequency parts of the signal and are represented by the father wavelet ф(x)
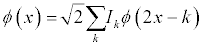
The details are the high frequency parts of the signal and are represented using the mother wavelet Ѱ(t) which is derived from the father wavelet using:
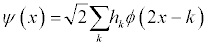
The coefficients Ik and hk are respectively the low and high pass filter coefficients and are calculated using:
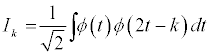
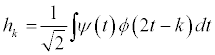
The projections of the original signal onto the father and mother wavelets defined above through scaling and translations result in the wavelet coefficients of approximation (sJ,k) and detail (d1,k, d2,k, …, dJ,k) where max{J} = log2(T) such that
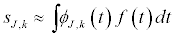
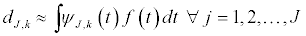
Thus, the wavelet representation of a signal f(t) can be expressed as:
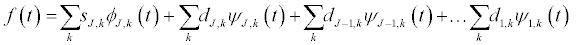
where J is the number of multi resolution level and k ranges from 1 to the number of coefficients in each level.
We can thus reconstruct the original time series signal using relation
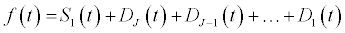
where:
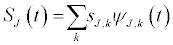
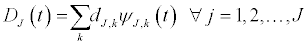
According to the principal energy conservation of the wavelet transform the variance of signal f(t) is reconstructed from the variance estimates at each scale j.
Duration model theory
Consider a N state duration model such that
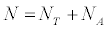
where:
NT ≅number of Transient states
NA ≅ number of Absorbing states
N ≅ number of Absorbing states
For the above, transition probabilities can be computed using
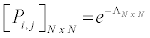
where: 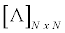 is the transition intensity matrix and
is the transition intensity matrix and
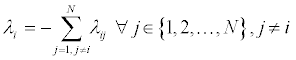
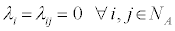
Now, using the Cox model for transition intensities we get
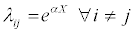
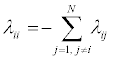
where:
[α]1 x M and XMx1 are factors affecting the transition intensities Finally, the likelihood function to be maximized is computed using the equation
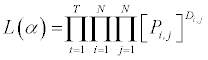
where:
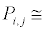 transition probability matrix for one period transition
transition probability matrix for one period transition
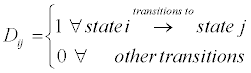
We model economic activity using a measure RGDP as discussed in the Data and Methodology section. The yield spread is computed using the difference between the yields of the ten-year government bond rate and three monthly (91 day) Treasury bill. We use quarterly data series ranging over 69 quarters starting from December 1995 to December 2012. As wavelet analysis warrants the data points in 2n we perform the wavelet analysis with respect to the Daubechies basis of order 2 (db4). This decomposition of the real GDP as well as the lagged yield spread splits the time series into 4 orthogonal components d1, d2, d3 and a3 where d1, d2, d3 comprise the detail components while a4 gives the long run trend for the individual data series. Each one of the decomposed series can be viewed as a time-scale representation of the original series. The time scale d1 represents the highest frequency component representing cycles that occur with a periodicity of 2 to 4 quarters, d2 stands for the next finest level in the series and represents cycles that occur with a periodicity of 4 to 8 quarters. The component d3 represents medium frequency component representing cycles that occur with a periodicity of 8 to 16 quarters. Finally, the component a3 stands for a time horizon more than 16 quarters (more than 4 years). The decomposition level is a function of the sample length and hence was restricted to 4 because of the small range of the available data. Each of the resulting time scale component is used a variable and is defined in Appendix I. A complete summary statistics for the variables used in the paper is shown in Table 1. We perform least squared regression at each frequency component to find the impact of yield spread on economic growth as modeled by the growth in real GDP. The regression results are summarized in Table 2. From the results it is clear that the best estimate, in terms of statistical significance, for economic activity as measured by yield spread is obtained at frequency components representing cycles with periodicity of 8 to 16 quarters (2 to 4 years). This is in line with our expectation that monetary policy effects on economic growth are realized only over longer horizons. A point I would like to mention here is that for India election cycles of 5 years come with 4 years of fiscal budget where policy issues are tackled and 1 year of Vote on Account which basically does not do much change than a mere formality of accounting presentation. Thus our results of time intervals seem to be matching the frequency of market and political cycles. Next, we use the filtered frequency components for real GDP growth rate and yield spread with the best regression result to compute state transition probabilities using cox intensity based duration model. We model the economy into two transient states: 1) Economic slowdown and 2) Economic expansion. State transition from slowdown to expansion occurs when at least two previous quarters exhibit positive growth. Similarly, a state transition from expansion to slowdown occurs when at least two previous quarters exhibit negative growth. Table 3 summarizes the results obtained both for the null model as well as the alternate model which uses the yield spread to in computing state transition probabilities for the real GDP growth as modeled by the cox intensity based duration model. The results in Table 3 clearly reject the null model for the alternate model giving further evidence that the monetary policy via yield spread affects real GDP growth but over longer (2 to 4 years) horizons of time. An in sample prediction for the state of the economy 4 quarters ahead, using the model parameters as summarized in Table 3, resulted in accurately identifying 50 out of the 68 transitions. Of these there 24 transitions when the economy was in expansion in the current quarter but entered into slowdown four quarters from then, 18 were accurately identified. This reiterates the impact of yield spread on real economic activity in India. The results justify the use of the yield curve as a leading indicator of macro-economic activity when studied over longer horizons of time.
| Variable Name | Label | Variable Definition |
|---|---|---|
| Growth in Real GDP at factor cost | RGDP | Ratio of Nominal GDP at factor cost to inflation as measured by WPI |
| Approximation wave of Real GDP | RGDPa3 | Frequency component of Real GDP representing cycles with periodicity greater than 16(24) Quarters |
| Detail(D3) wave of Real GDP | RGDPd3 | Frequency component of Real GDP representing cycles with periodicity between 8(23) and 16(24) Quarters |
| Detail(D2) wave of Real GDP | RGDPd2 | Frequency component of Real GDP representing cycles with periodicity between 4(22) and 8(23) Quarters |
| Detail(D1) wave of Real GDP | RGDPd1 | Frequency component of Real GDP representing cycles with periodicity between 2(21) and 4(22) Quarters |
| Yield Spread lagged by 4 Quarters | PYSL4Q | Percentage Value of Yield Spread lagged by 4 quarters |
| Approximation wave of lagged Yield Spread | PYSL4Qa3 | Frequency component of percentage value of Lagged Yield Spread representing cycles with periodicity greater than 16(24) Quarters |
| Detail(D3) wave of lagged Yield Spread | PYSL4Qd3 | Frequency component of percentage value of Lagged Yield Spread representing cycles with periodicity between 8(23) and 16(24) Quarters |
| Detail(D2) wave of lagged Yield Spread | PYSL4Qd2 | Frequency component of percentage value of Lagged Yield Spread representing cycles with periodicity between 4(22) and 8(23) Quarters |
| Detail(D1) wave of lagged Yield Spread | PYSL4Qd1 | Frequency component of percentage value of Lagged Yield Spread representing cycles with periodicity between 2(21) and 4(22) Quarters |
Table 1: Summary Statistics - This table provides summary statistics of the variables used in regressions and duration models. All variables are defined in the Appendix. The variables defined cover a period of 69 Quarters starting from December 1995 to December 2012.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| VARIABLES | Obs | Mean | Std.Dev | Min | Max |
| RGDP | 69 | 0.0137 | 0.0232 | -0.0281 | 0.0598 |
| RGDPa3 | 69 | 0.0135 | 0.0130 | -0.0155 | 0.0327 |
| RGDPd3 | 69 | 0.0004 | 0.0154 | -0.0330 | 0.0377 |
| RGDPd2 | 69 | -0.0001 | 0.0106 | -0.0294 | 0.0270 |
| RGDPd1 | 69 | 0.0000 | 0.0040 | -0.0106 | 0.0098 |
| PYSL4Q | 69 | 1.8400 | 1.3490 | -0.0967 | 5.6330 |
| PYSL4Qa3 | 69 | 1.8930 | 0.9300 | 0.4140 | 3.9220 |
| PYSL4Qd3 | 69 | -0.0552 | 0.7030 | -1.3630 | 1.9310 |
| PYSL4Qd2 | 69 | 0.0021 | 0.3830 | -0.9550 | 1.0150 |
| PYSL4Qd1 | 69 | 0.0007 | 0.2580 | -0.5430 | 0.5140 |
Table 2: The figure summarizes regression results of real GDP against the yield spread. Control variables are yield spread filtered over various frequency bands. All variables are defined in the Appendix. The variables defined cover a period of 69 Quarters starting from December 1995 to December 2012. Standard errors in parentheses. ***Significance at 1%, **significance at 5%, *significance at 10%
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
|---|---|---|---|---|---|---|---|---|---|---|
| RGDP | RGDPa3 | RGDPd3 | RGDPd2 | RGDPd1 | ||||||
| Variables | coef | Se | coef | se | coef | se | coef | se | coef | se |
| PYSL4Q | -0.0039* | (0.0020) | ||||||||
| PYSL4Qa3 | -0.0021 | (0.0017) | ||||||||
| PYSL4Qd3 | -0.0103*** | (0.0024) | ||||||||
| PYSL4Qd2 | 0.0009 | (0.0034) | ||||||||
| PYSL4Qd1 | 0.0002 | (0.0019) | ||||||||
| Constant | 0.0209*** | (0.0046) | 0.0175*** | (0.0035) | -0.0002 | (0.0017) | -0.0001 | (0.0013) | -0.0000 | (0.0005) |
| Observations | 69 | 69 | 69 | 69 | 69 | |||||
| R-squared | 0.0526 | 0.0230 | 0.2227 | 0.0011 | 0.0001 | |||||
Table 3: The table shows the impact of yield spread in computing state transition probabilities for Real GDP fitted to cox intensity based duration model. All variables are defined in the Appendix. The variables defined cover a period of 69 Quarters starting from December 1995 to December 2012. Standard errors in parentheses. ***Significance at 1%, **significance at 5%, *significance at 10%
Our study suggests strong empirical evidence of the impact of the yield curve in predicting economic slowdowns in India. Monetary policy directly affects the yield curve which acts as a leading indicator in predicting the macro economic activity over longer horizons of time with strongest impact observed over periods of 8 to 16 quarters (2 to 4 years).