Journal of Biomedical Engineering and Medical Devices
Open Access
ISSN: 2475-7586
ISSN: 2475-7586
Research Article - (2016) Volume 1, Issue 2
Keywords: Saccadic eye movement; Double-step stimulus; Response pattern; Latent period; Amplitude; Inter-saccade interval; Oculomotor plant; Agonist neural input; Saccade programming
Saccades are the fastest eye movements that enable us to rapidly redirect our line of sight from one target to another one. They are conjugate and ballistic, with a typical duration of 30-100 ms and a latency of 100-300 ms when triggered by visual stimuli. The latency is thought to be the time interval during which the CNS determines whether to make a saccade, and, if so, calculates the distance the eyeball is to be moved, transforming retinal errors into transient muscle activity. Cognitive control and decision-making take place during this preparation period. How will saccades be modified in “mid-flight” by factors that are applied before the eye starts to move? Westheimer first developed the double-step paradigm by presenting subjects with two targets along a horizontal plane with a varying interstimulus interval separating the two targets [1]. Previous studies indicate the “parallel programing” mechanism, which the second saccade programming can take place while the first saccade is being programmed and executed [2-4]. The visual information can be acquired continuously to modify saccade amplitude until about 70-100 ms prior to the eye movement onset, and the CNS appears able to overlap some presaccadic planning [5-8]. Saccade sequence planning is always discussed by analyzing response localization, latency, and intersaccade interval under the double-step condition [2-11].
In addition to the investigation of saccade characteristics, many studies focus on modeling eye plant dynamics in response to saccade controllers. The work provided in this paper is based on a linear 3rdorder model of the oculomotor plant for horizontal saccades by Enderle and coworkers [12-14], while the neural inputs are described by pulse-slide-step waveforms with a post inhibitory rebound burst (PIRB) based on a time-optimal controller [12,13,15-18]. The oculomotor plant consists of the eyeball, a passive Voigt element, and two extraocular muscles, and it has accurate nonlinear force-velocity and length-tension relationships that agree with the data [12,13,17,18]. The inputs to the muscles are the agonist and antagonist active-state tensions, which are derived from a low-pass filtering of the saccadic neural innervation signals. In agreement with the time-optimal controller, previous studies have presented the neural input properties for goal-oriented saccades that trigged by one-step (from primary position to a peripheral position) visual or auditory stimuli [12,19]. Agonist pulse magnitude shows a linear increase in small saccades, since the number of firing neurons determines the pulse size. Agonist pulse magnitude remains approximately constant for larger saccades over 7 degrees, indicating all neurons fire maximally, and the pulse duration increases as a function of saccade amplitude. Here, our interest is centered on the neural inputs to the oculomotor plant under the double-step paradigm. The study described here expands on our previous work [19] and further supports the muscle models as well as the theory of the time-optimal controller under physiological constraints.
Subjects
Four subjects (two males and two females, aged 20-30) participated this study. All demonstrated normal or corrected-to-normal visions, and none of them disclosed any history of visual or vestibular disorders. The subjects were trained on tasks of regular goal-oriented saccade experiments (one-step) before performing the double-step saccades.
Apparatus
Subjects were seated 830 mm in front of a computer monitor with head stabilized by a high speed eye tracking device (1250 Hz sample rate, by SensoMotoric Instruments (SMI)). The visual targets consisted of white solid dots (4 mm diameter) on a gray background and were displayed on the screen. Seven target positions were presented to the subject at angles of 5°, 10° and 20° from the center (0°) to left or right in the horizontal plane.
The experiments were conducted using custom written software, while data were collected using the eye tracker implemented in the iView X™ system by SMI. All the tests were performed in an independent, quiet room with normal illumination.
Experiment design
The subjects were instructed to maintain their eyes on the visual target by moving their eyes as fast as possible. A saccade was made when the active target was switched off and another target was switched on. There were three test sessions with the first peripheral target’s duration (S1, shown in Figure 1(a)) set as 70, 140 and 210 ms. The target stepped twice centrifugally in the same direction. Each session included multiple trials, following 0°-5°-10° or 0°-10°-20° double-step displacements, to right or left. The duration of any center or second peripheral stimulus in a trial was random from 3000 to 5000 ms.
Figure 1: Schematic representation of the sequence of target events (a), and saccadic responses: (b) double-step and (c) single-step. A is saccade amplitude, L is latency, and Dur is saccade duration. D is delay, which is defined as the time between the end of first peripheral target presentation and the onset of initial saccade (L1- S1). Int is the inter-saccade interval in response.
Data processing and analysis
Raw data contained pupil and gaze information were generated automatically by the iView X™ system. Gaze data from the left eye were recorded in pixels, and then converted to degrees. The converted eye position data were first plotted for quality and response pattern examination. If two steps were obtained, they were separated for further analysis.
Acceptable saccades data were run in a FORTRAN program which was used to compute parameter estimates for the model of horizontal saccadic eye movements [12,13]. Graphs in Figure 2 are based on parameter estimates calculated by the system identification technique for a double-step response, where the first step (Figure 2 (a)) and second step (Figure 2 (b)) are analyzed separately. The estimated agonist and antagonist neural inputs, Nag and Nant, and active-state tensions, Fag and Fant, are presented in the first two rows. As shown in the bottom rows, the model predictions match amplitude data, datacalculated velocity (derivative of the amplitude) and data-calculated acceleration (second derivative of the amplitude) very well. The accuracy demonstrated in this graph is consistent with the other saccades analyzed. 378 trials of saccade data that contained either double-step (Figure 1(b)) or single-step (Figure 1(c)) responses were successfully analyzed.
Figure 2: Model estimated neural inputs Nag and Nant (red line), active-state tensions Fag and Fant (blue line) of three saccades. Also shown are the model predictions using the parameter estimates from the system identification technique for amplitude, velocity, acceleration (blue line), and the experimental data (red line). (a): the first step of a 0°-5°-10° response with a glissade. (b): the second step of a same trial.
(Note: “double-step” and “single-step” are both saccade responses under the double-step stimulus paradigm. “One-step” refers to the response when only one peripheral target is presented.)
Saccade response pattern, accuracy and amplitude
Saccade response patterns are related with the duration of the first peripheral target (also defined as inter-stimulus interval, S1). Figure 3 shows the occurrence rate of a double-step response under two trial patterns. When inter-stimulus interval S1 is relatively small (70 ms), subjects are more likely to follow the second target directly without landing on the first peripheral target (shown as a single-step response), resulting a smaller probability of double-step response. As the inter- stimulus interval increases, double-step responses are obtained in almost all tests. It is also shown that double-step responses have a higher chance to appear in 0°-10°-20° trials.
Under the double-step paradigm, the initial/primary saccade is defined as the first step of a double-step response, or the single-step response. In order to determine the saccade accuracy, initial/primary saccade amplitude is compared with the desired target amplitude. As shown in Figure 4(a), saccade amplitude of the singe-step responses (As) has a relatively low variance, while undershoot happens frequently when respond to a +/-20° target (average As=+18.17° and -18.43°). Regarding to the first steps (A1), average saccade amplitudes are +4.96°, -6.12°, +9.77°, -10.21° in response to +/-5°, +/-10° targets, respectively, and they show a slight higher variance (Figure 4(b)). Further analysis includes percent error calculations (Figure 5), following
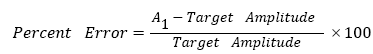
Figure 5: Percent error of the first step amplitude. In (a) 0°-5°-10° experiments, 86% of the -5° eye movements have percent error of A1>0, and 60% of the +5° eye movements have percent error of A1<0. In (b) 0°-10°-20° experiments, 59% of the -10° eye movements have percent error of A1>0, and 65% of the +10° eye movements have percent error of A1<0. Data are from all subjects.
where a positive percent error indicates an overshoot (absolute saccade amplitude is larger than absolute target amplitude) and a negative percent error indicates an undershoot (absolute saccade amplitude is smaller than absolute target amplitude). In abduction (-5° and -10° movement for the left eye) double-step saccades, the eye always first lands on a position that between the locations of the two peripheral targets, resulting a first-step overshoot, while in adduction (+5° and +10° movement for the left eye) double-step saccades, there’s a higher chance of performing a first-step undershoot. This is more obvious in 0°-5°-10° experiments, and the saccade accuracy is very high in 0°-10°-20° experiments.
Saccade amplitude transition function (ATF) was introduced by Becker and Jürgens [2], where the initial/primary response amplitude is plotted verses delay D (defined as the time between the end of first peripheral target presentation and the onset of initial saccade). Figure 6 shows the ATF, indicating that for delays less than about 110 ms, subjects make double-step responses (the amplitude of the first steps is plotted). Average saccade amplitude gradually increases in both directions for delays from 110 to 140 ms (in 0°-5°-10° experiments) or 170 ms (in 0°-10°-20° experiments), and it’s between the locations of the first and second targets. Amplitude then stays relatively constant again when delays get even longer, which means that subjects make a single-step response directly to the second target location.
Saccade latency and inter-saccade interval
Figure 7 presents the saccade latency distribution of double-step responses. It shows that the saccade latency of the second steps is sometimes longer than the latency of initial/primary saccades that of similar amplitude. Average saccade latencies of two representative subjects are listed in Table 1.
| Subject 1 | Subject 2 | ||
|---|---|---|---|
| 0°-5°-10° Pattern | L1 (ms) | 186.66 | 183.42 |
| L2 (ms) | 246.96 | 213.31 | |
| 0°-10°-20° Pattern | L1 (ms) | 196.21 | 175.83 |
| L2 (ms) | 256.21 | 234.82 | |
Table 1: Average saccade latency.
Second-step saccade latency L2 of two subjects is plotted against time delay as shown in Figure 8. At delays less than 40-50 ms, L2 is roughly constant for both subjects, while subject 1 has a slight higher value than subject 2. When delays fall in the range from 50 to 150 ms, L2 shows a linear increase, where the approximate slope is 1.
Inter-saccade interval is defined as the time between the onset of the first saccade and the onset of the second saccade in a double-step response (Figure 1). Plots of inter-saccade interval versus time delay D for two representative subjects are shown in Figure 9. Despite the individual variability, inter-saccade interval trends to decrease with time delay with a slope around negative 0.4, while the change is steeper when delays are less than 50 ms.
Agonist pulse magnitude
Parameter estimations were calculated by the system identification technique [12]. Agonist pulse magnitude is defined as the peak magnitude of the agonist neural input, as shown in Figure 2 first row (red). The results of the model estimation are shown in Figure 10, including the pulse magnitude of single-step and the two separate steps in double-step responses for two representative subjects. Overall, the agonist pulse magnitude of subject 1 is around 0.5 N higher than that of subject 2, and subject 2’s data fall in the same range as our previous visual goal-oriented one-step saccade experiment data [19]. For both subjects, pulse magnitude increases linearly with small saccade amplitude under 7°, and stay relatively constant when saccade amplitude is larger. Note that for small saccades around 5°, the trend lines for the first and second steps pulse magnitude show obvious difference, while no such difference is illustrated in larger saccades around 10°. This is observed in all subjects’ data. In Figure 10(b), subject 2 shows a relatively high agonist pulse magnitude in second steps of +10° saccades. This is a particular case and it is not obtained in the data of other subjects. Agonist pulse magnitude of single-step and double-step responses falls into a similar range.
In previous studies of double-step saccades, target separations (step) were set at large amplitude (12°, 15°, 45°, etc.) in horizontal plane [2,3,20], while others displayed targets in 2-D coordinates [4,5,7,8]. Our experiment design focuses on horizontal saccades with smaller stimulus steps (5° and 10°) following “staircase” pattern, which allows us to compare the characteristics and neural input properties with visual one-step goal-oriented saccades, and thus expands the saccade system investigation. The 3rd-order linear saccade model that supports the data analysis in this study has been fully examined before [12-14,17-19], thus it can be further applied to the current study, providing accurate saccade characteristics and neural input estimations. Statistical analysis of a large human saccade data set provides reliable conclusions of the response properties under the double-step paradigm.
Saccade characteristics and response properties
Saccade response patterns are related with the inter-stimulus interval and delay D, which is the time between the end of the first target presentation and the onset of the initial/primary saccade. Our saccade transition function (ATF) shows single-step responses occur with long delays, while double-step responses happen with shorter delays. This means the retinal error can be immediately updated when a second target is applied, the programming of the preceding saccade ends and the programming of the saccade to the new target starts at once. As the inter-stimulus interval increases, the preceding saccade programming cannot be modified [2,3,5,20]. Since double-step responses present when delay is shorter than around 110 ms, and the average latency of the first steps is 180-200 ms, it indicates the visual information can be acquired continuously to modify saccade amplitude until about 70-90 ms prior to eye movement onset. We also find that it’s more frequent to skip the landing on the first peripheral targets when the two targets are closer to the primary position (center) (Figure 3).
Overall, saccade accuracy is still very high under the visual doublestep paradigm. For the single-step responses caught in 0°-10°-20° experiments, the saccade amplitude is slight less than desired target amplitude. Such undershoot suggests the retinal error is “updated” rather than directly obtained. In double-step responses, a significant high occurrence rate of first-step overshoot is found in abduction eye movements. This probably accounts for the fact that the lateral rectus eye muscle is usually stronger than the medial rectus muscle.
The timing properties of double-step saccades indicate the saccade programming mechanism. Previous studies have suggested the “parallel programming”, which the programming of a second saccade can be initiated prior to the execution of a preceding saccade [2-4,7]. Our findings further support this conclusion. If the two saccades are programmed in paralleled, each step is only responsible to one of the two targets, and the second step should occur in a relatively fixed period after the onset of the second target, regardless of the timing of the initial saccade [7]. Since the fact that saccade latency is usually independent of saccade amplitude and show a relatively great variance, the range of L2 distribution shown in Figure 7 can be accepted as a “fixed area”. Moreover, from the logic of the parallel, independent saccade programming suggests that the inter-saccade interval should be inversely related to the delay with an ideal slope of negative one [2,4,7]. Our data in Figure 9 show an overall slope of around -0.4, while the change is much steeper when delay is less than 50 ms. Shorter inter-saccade intervals with longer delays suggest the programming of two sequential saccades may be overlapped. Constant L2 with short delays less than 50 ms (Figure 8) also supports such parallel programming mechanism. Note that the mean latency of the second steps is generally longer than that of the first steps, and L2 is larger at longer delays. These indicate a reduction in the speed of processing the second saccades.
Neural input estimation
In the saccadic model used here, the overall neural input increases as the amplitude of saccades increases up to 7° due to the increasing number of firing neurons, with all neurons firing maximally. In large saccades, all neurons fire maximally, which results in a relatively constant pulse magnitude [12-14]. Estimated agonist pulse magnitude doesn’t significantly increase with increasing saccade amplitude for saccades larger than about 7°, but there is a more obvious linear increase for small saccades under 7° (Figure 10). For both subjects, the pulse magnitude appears similar for the initial/primary and the secondary saccades of size around 10°. This is true because only the retinal error determines the active neuron population.
A significant finding can be observed in the agonist pulse magnitude of saccades around 5°: with a similar trending slope, the pulse magnitude of the first-step saccades is different (in most cases, lower) from that of the second-step saccades (Figure 10). Smaller saccades have fewer actively firing agonist neurons than larger saccades, thus the firing synchrony of individual neurons has a greater impact on the overall neural input for small saccades, and any lack of synchrony causes the overall agonist input to be smaller [12-14]. Our results indicate that for the saccade responsible neurons in the superior colliculus, a second presented visual target may affect their synchrony of firing. Since the agonist pulse magnitude between the first and the second steps in larger saccades are similar, the number of firing neurons is not affected by the double-step stimulus.
Two sequential visual targets are presented with varying inter-stimulus interval to trigger double-step saccades. Saccade characteristics and neural input properties are estimated using a 3rd-order linear horizontal saccadic eye movement model. The analysis of response patterns with saccade amplitude, latency, and inter-saccade interval provides evidence of parallel programming mechanism. While the programming of a second saccade can be initiated prior to the execution of a preceding saccade, there may be a penalty associated with a concurrently-programmed second saccade, resulting a longer latency (L2). Supported by the estimated agonist neural input, the double-step stimulus doesn’t affect the number of firing neurons, but the synchrony of firing. The study described here expands our previous work and further supports the muscle model as well as the theory of the time-optimal saccade controller under physiological constraints.