Journal of Geology & Geophysics
Open Access
ISSN: 2381-8719
ISSN: 2381-8719
Research Article - (2014) Volume 3, Issue 2
A detailed study to propose new design support systems for underground mine was carried out in this paper. The depth was increased to develop the production in accordance with the vein.The cut and fill mining method was selected for this mine in line with the geometry of vein, topographic specifications, and annual production rates.Excavationsize, distance between stope and decline, depth, and the impact of fault governedthe induced stresses. Different depths in multiple excavations were analyzed in this study especially on decline area. The rock properties of investigated areawere defined from the field and laboratory test for each rock type. Support systems for the decline were designed based on the suggestions of the Rock Mass Rating (RMR) system and the Q system for rock mass classification. Induced stress on different levels were calculated to define Stress Reduction Factor (SRF) and applied to predict the support system by Q system. New method namely Hybrid Numerical Empirical Model was developed to support requirement analysis in cut and fill mining method. The support system requirement influenced by depth. The shotcrete will be thicker and rock bolt space more closely as increasing the depth.
Keywords: Support system,Underground mine, Cut and Fill, Rock mass, Hybrid numerical empirical model
Obtaining a stablethe underground mining isone of the main concernsforanunderground mine engineer. A stable underground mining is determined by the suitability and economical support system with a convenient excavation method.
Rock mass classifications are traditionally used to group areas with similar geomechanicalcharacteristics.This classifications is expectedto provide guidelines for stability performance, and to select appropriate support. The rock mass classifications have been successfully applied to many tunnel construction designs. Two widely-used rock mass classifications in underground mines are Rock Mass Rating (RMR) and Norwegian Geotechnical Institute (NGI, Q-system).
The main objective of this paper is to predict the required support systems for cut and fill underground mine which focus on decline main ways. In this study, support system requirements were calculated based on rock mass classification systems, and considered of induced stresses. This research is important to propose support systems for underground mine openings on different level activities.
Kirsch, was the first publisher for the induced stresses distributions of a circular tunnel [1].Hoek and Brown, developedanadditional tool that can be predicting the induced stresses distributions [2]. The impact of induced stresses on stope stability was applied to Mathews empirical stability graph method [3,4]. Rock massclassification, Qsystem is proposed for predicting underground support system [5,6]. The effects of induced stresses are determined by comparing the maximum tangential stresses (σθ) to the intact uniaxial compressive strength (σc) in a similar manner to the Mathews’ method. Wattimena, 2003 applied the Mathews’methodon block caving mines in Australia and proposed a Hybrid NumericalEmpirical Model (HNEM) to predict induced stresses and to calculate the Q system for estimating support requirement on undercut and production levels [7].
The field site for this study is Cibaliungunderground gold minewhichlocated in the western part of Java Island, Indonesia (Figure 1). The resource is estimated to be approximately 1.5 million wmt gold with grade is estimatedto be 9.8 ppm.The type of ore is vein with low sulphidation.Geological mapping and geotechnical description were conducted in the field.
The host rock of Cibaliung deposit is in Honje Formation consists of andesite, basaltic andesite volcanic and volcanic breccia intercalated with tuffaceous sediment [8]. Andesite rock types, consists of andesite, andesite breccia, polymictic and monomictic breccia. Those host rocks are altered by chlorite-adularia and smectite-illite. The type of ore is a vein with low sulphidation epithermal deposit dominated by quartz vein. This vein follows the Cibaliung fault within NNW-striking/ENEdipping, with two shoot target Cikoneng and Cibitung ore shoot. The Cikoneng ore geometry is 250 m length, 2-10 m width and 200 m depth, whereas Cibitung shoot geometry is 150 m length, 2-15 m width and 300 m depth with dip of ore is 80o. Some minor faults occur throughout the hanging wall excavation with strike NE-SW dip 75°. Angel of this fault with axis of tunnel is 21°.The geology of Cibaliung can be seen in Figure 2 [9].
Three main rock types, quartz vein as ore body, andesite-breccia altered by chlorite-adularia on footwall abundance, and andesitebreccia altered by smectite-illite dominant on hanging wall rock are observed in the study area.
The rock mass rating (RMR) system [10,11] and the Qsystem developed by the Norwegian Geotechnical Institute [5] were used to classify rock masses. The physical and mechanical properties of the rocks were investigated based on rock mass classifications from the field and laboratory studies on intact rock samples.
These tests coveran evaluation of uniaxial compressive strength (σc), tensile strength (σt), Young’s modulus (E), Poisson’s ratio (v), density (ρ), internal friction angle (ϕ), and cohesion (c). Uniaxial compressive strength, triaxial compressive strength, Brazilian and density tests were conducted in accordance with the ISRM standard. The values of minimum and maximum UCS varies, with the lower mean of UCS is in hanging wall rock. The results of rock properties tests are summarized in Table 1.
| Parameter | Breccia Smectite (hw) | Breccia Chlorite (fw) | Quartz vein (Stope) |
||||
| min | max | mean | min | max | mean | ||
| σc (MPa) | 2 | 68 | 24 | 5 | 153 | 51 | 74 |
| E (GPa) | 1.38 | 37 | 21 | 3.21 | 97 | 57 | 2.52 |
| v | 0.25 | 0.62 | 0.36 | 0.17 | 0.25 | 0.21 | 0.35 |
| C (MPa) | 0.2 | 19 | 11 | 0.44 | 35 | 22 | 0.345 |
| ø (…o) | 35.5 | 41 | 38 | 39 | 40.5 | 33 | 38.6 |
| σt(MPa) | 0.004 | 3.5 | 2.45 | 0.018 | 9 | 6.71 | 0.01 |
| p (ton/m3) | 2.50 | 2.51 | 2.505 | 2.56 | 2.60 | 2.58 | 2.70 |
Table 1: Mechanical and physical properties of Cibaliung rock materials.
In this study, RMR and Q-system classifications were applied rock mass characterization. Some parameters were determined for RMR, includes uniaxial compressive strength (UCS), Rock Quality Designation (RQD), discontinuity spacing, discontinuity conditions, and groundwater conditions. The results of this study are shown in Table 2 to Table 4 for RMR.RQD, number of joint sets (Jn), joint surface roughness (Jr), joint weathering and alteration (Ja), joint water reduction factor (Jw), and stress reduction factor (SRF) are parameters for Q to quantify rock mass. RMR rating can be determined from the classification proposed by Bieniawski, [10]. Meanwhile, the Q value of a rock mass can be calculated by the equation given below, as determined in the classification proposed by Barton et al. [5].
| Parameters | Description | Rating | Description | Rating |
| Location(chainage) | 565-568 | 591-593 | ||
| σc, Mpa | 2-68 | 2-7 | 2-68 | 2-7 |
| RQD (%) | 55 | 13 | 55 | 13 |
| Spacing of discontinuous (cm) | 15-60 | 8 | 15-60 | 8 |
| Condition of discontinuous | Slickenslide to slightly rough surfaces | 10 | Slickenslide to slightly rough surfaces | 19 |
| Groundwater | Damp to dry | 10 | Dry | 15 |
| Effect discontinuous | Very Unfavourable | -12 | Unfavourable | -10 |
| Total RMR | 30-31 | 48 | ||
| Classification | Poor | Fair |
Table 2: The rock mass classification of breccia smectite (hanging wall) based on the RMR.
| Parameters | Description | Rating | Description | Rating |
| Location (chainage) | 791-792 | 814-817 | ||
| σc, Mpa | 5-153 | 2-12 | 5-153 | 2-12 |
| RQD (%) | 60 | 13 | 65 | 13 |
| Spacing of discontinuous (cm) | 20-60 | 10 | 20-60 | 10 |
| Condition of discontinuous | Slickenslide to slightly rough surfaces | 20 | Slickenslide to slightly rough surfaces | 20 |
| Groundwater | Wet to damp | 8 | Damp to dry | 13 |
| Effect discontinuous | Unfavourable | -8 | Unfavourable | -1 |
| Total RMR | 48 | 61 | ||
| Classification | Fair | Good |
Table 3: The rock mass classification of breccia chlorite (footwall) based on the RMR.
| Parameters | Description | Rating | Description | Rating |
| Location (chainage) | Xcut 4 1.6 | Xcut 4 12.5 | ||
| σc, Mpa | 74 | 7 | 74 | 7 |
| RQD (%) | 63 | 13 | 70-77 | 13-17 |
| Spacing of discontinuous (cm) | 20-60 | 10 | >200 | 20 |
| Condition of discontinuous | Slickenslide to slightly rough surfaces | 19 | Slickenslide to slightly rough surfaces | 19 |
| Groundwater | Wet to damp | 10 | Wet to damp | 10 |
| Effect discontinuous | Fair to unfavourable | -5 | Fair to unfavourable | -5 |
| Total RMR | 54 | 64 | ||
| Classification | fair | Good |
Table 4: The rock mass classification of quartz vein (stope) based on the RMR.
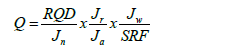 (1)
(1)
Design of support systems was carried out by considering the in situ stress, stress around the openings, and evaluation of failure conditions. In situ stress was calculated from equation (2) for different levels within each geological formation.
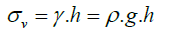 (2)
(2)
Where:
σv= vertical stress (MPa)
γ = specific weight of the rock properties (MN/m3)
h = depth of overburden (m)
ρ = average density of rock properties (ton/m3)
g = acceleration due to gravity (m/s2)
Hoek and Brown, proposed equations to calculate tangential stress around the roof and the wall of the openings on equation (3) and equation (4), respectively. The constants A and B are taken as 3.2 and 2.3 for a horseshoe-shaped gallery [2].
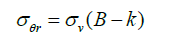 (3)
(3)
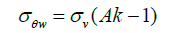 (4)
(4)
Since the influence of multiple excavations could not be predicted by the above mentioned equations, numerical modeling analysis is a proposed as a solution. Therefore Phase2® software is useful to predict induced stress on two dimensions.
The tangential stresses are determined near the opening on the roof and wall side. Figure 3 shows the initial condition for numerical modeling.The results of tangential stresses by numerical modeling are given in Table 5 and Figure 4 shows the graphic of induced stress on different levels.
| Distance | 5 | 10 | 20 | 30 | 40 | ||||||
| depth | hw | fw | hw | fw | hw | fw | Hw | fw | Hw | fw | |
| wall side | 88 | 3.201 | 3.830 | 2.509 | 2.708 | 2.274 | 2.376 | 2.167 | 2.246 | 2.132 | 2.216 |
| 150 | 5.378 | 6.383 | 4.210 | 4.483 | 3.747 | 3.920 | 3.630 | 3.770 | 3.604 | 3.737 | |
| 200 | 7.139 | 8.440 | 5.602 | 5.882 | 4.985 | 5.167 | 4.871 | 5.054 | 4.749 | 4.963 | |
| 300 | 10.681 | 12.518 | 8.389 | 8.728 | 7.429 | 7.614 | 7.254 | 7.472 | 7.155 | 7.396 | |
| roof | 88 | 5.292 | 6.237 | 5.832 | 6.015 | 6.228 | 6.253 | 6.319 | 6.349 | 6.306 | 6.256 |
| 150 | 9.551 | 10.508 | 10.044 | 10.849 | 10.904 | 11.382 | 11.265 | 11.168 | 10.828 | 11.700 | |
| 200 | 11.904 | 13.149 | 13.649 | 13.866 | 13.986 | 14.577 | 15.135 | 14.001 | 14.382 | 15.382 | |
| 300 | 18.477 | 21.166 | 20.536 | 21.367 | 20.504 | 20.734 | 22.066 | 21.576 | 22.836 | 22.741 | |
Table 5: The predicted tangential stress (MPa) in hanging wall (hw) and footwall (fw) declines from numerical modeling.
Tangential stresses at the boundaries increase as increasing depth of excavations. In general, the tangentialstresses at the boundaries of both hanging wall and footwall decline excavations in the sidewall decreased with the distance from the decline to the stope. Significant tangential stresses decreases was observed when the distance changed from 5 m to 10 m. The tangential stresses are relatively constant when the distance between declines and stope up to 30 m on the hanging wall decline and 20 m on the footwall decline.
The tangential stresses in the roof increase with increasing of depth. The trend of tangential stress for both hanging wall and footwall declines in the roofwas found to be relatively constant as increasing distance between declines and stope. These results are the basis data to predict damage and calculate the support requirement. Tangential stress on the roof is higher than that on the wall and considered to support analysis.
The relation between intact rock material strength and tangential stress can be used to predict rock burst in underground. A high value for tangential stresses is a good indicator for rock burst. Rock burst potentially damage classified by Grimstad and Barton [6]. The classifications are summarized in Table 6. Calculated values between intact rock and tangential stress to predict rock burst potential are given in Table 7. The intact uniaxial strength of hanging wall decline was 24 MPa and footwall decline was 51 MPa.
| The value of the ratio sc/sq | Description |
| >100 | Near surface, low stress, open joints No rock spalling/stable/medium, favorable stress condition/No rock stress induced instability |
| 100-3 | |
| 3-2 | Low rock spalling/minor spalling/high stress, very tight structure/high stress, slightly loosening |
| 2-1.5 | Moderate rock spalling/severe spalling/moderate slabbing after 1 h/light rock burst or spalling |
| 1.5-1 | High rock spalling/heavy support required/slabing and rock burst/heavy rock burst |
| <1 | Heavy rock burst/severe rock burst |
Table 6: Rock burst classifications by Grimstad& Barton [6].
| Position | Depth | Distance from HW decline to stope | Distance from FW decline to stope | ||||||||
| 5 | 10 | 20 | 30 | 40 | 5 | 10 | 20 | 30 | 40 | ||
| wall side | 88 | 7.50 | 9.57 | 10.55 | 11.08 | 11.26 | 13.32 | 18.83 | 21.46 | 22.71 | 23.01 |
| 150 | 4.46 | 5.70 | 6.41 | 6.61 | 6.66 | 7.99 | 11.38 | 13.01 | 13.53 | 13.65 | |
| 200 | 3.36 | 4.28 | 4.81 | 4.93 | 5.05 | 6.04 | 8.67 | 9.87 | 10.09 | 10.28 | |
| 300 | 2.25 | 2.86 | 3.23 | 3.31 | 3.35 | 4.07 | 5.84 | 6.70 | 6.83 | 6.90 | |
| roof | 88 | 4.54 | 4.12 | 3.85 | 3.80 | 3.81 | 8.18 | 8.48 | 8.16 | 8.03 | 8.15 |
| 150 | 2.51 | 2.39 | 2.20 | 2.13 | 2.22 | 4.85 | 4.70 | 4.48 | 4.57 | 4.36 | |
| 200 | 2.02 | 1.76 | 1.72 | 1.59 | 1.67 | 3.88 | 3.68 | 3.50 | 3.64 | 3.32 | |
| 300 | 1.30 | 1.17 | 1.17 | 1.09 | 1.05 | 2.41 | 2.39 | 2.46 | 2.36 | 2.24 | |
Table 7: The value of ratio σc/σθ for calculating rock burst.
Based on the relation between intact rock and tangential stress, the damage potential in the roof is higher than that in the wall sides. Given the condition in the hanging wall,a rock damage will be more likely to occur in the hanging wall when comparedwith the footwall excavations. The results suggest that there will be minor rock spalling when the activities below 300 m depth in the wall sides on hanging wall. However, low to moderate rock spalling will take place in the roof when the mine activities occurs under 150-200 m depth. At the depth lower than 300 m, high rock spalling is predicted to occur and necessitating a heavy support. Although the condition on the footwall was observed to be relative stable, low rock spalling could occur at the depth below 300 m.
Bieniawski, proposed guidelines for excavation and support of 10 m span rock tunnels in accordance with the RMR system. The current support system in Cibaliung underground gold mine determined by using RMR. The support systems of individual openings were designed according to the surrounding rock mass characteristic. The equations proposed by Barton et al. [12] and Unal [13], which includes rock mass classifications, excavation width, span excavation, and material rock density was used to determine the splitset number and shotcrete thickness to support requirements [13].The results from equation 5 to equation 8 are shown in Table 8 and Table 9.
| Location | RMR | Width (m) | Rock load height (m) | Span (m) | Rock density (ton/m3) | Safety factor | Rock bolt | Rock bolt grouted | ||
| Bearing capacity (ton) | Number (pieces) | Bearing capacity (ton) | Number (pieces) | |||||||
| Hanging wall | 30 | 4.2 | 2.94 | 2.4 | 2.505 | 1.5 | 7 | 15.91 | 15 | 7.42 |
| 48 | 4.2 | 2.184 | 2.4 | 2.505 | 1.5 | 7 | 11.81 | 15 | 5.51 | |
| Footwall | 48 | 4.2 | 2.184 | 2.4 | 2.58 | 1.5 | 7 | 12.17 | 15 | 5.68 |
| 61 | 4.2 | 1.638 | 2.4 | 2.58 | 1.5 | 7 | 9.13 | 15 | 4.26 |
Table 8: The rock bolt requirement.
| Location | Geometry (m) | RMR | Rock load pressure (ton/m2) | USB shotcrete (ton/m2) | Safety factor | Rock density (ton/m3) |
Shotcrete thickness (m) |
| Hanging wall | 4.2 x 4.8 | 30 | 7.36 | 2500 | 1.5 | 2.505 | 0.040 |
| 4.2 x 4.8 | 48 | 5.47 | 2500 | 1.5 | 2.505 | 0.030 | |
| Footwall | 4.2 x 4.8 | 48 | 5.63 | 2500 | 1.5 | 2.580 | 0.031 |
| 4.2 x 4.8 | 61 | 4.22 | 2500 | 1.5 | 2.580 | 0.023 |
Table 9: The shotcrete thickness.
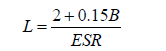 (5)
(5)
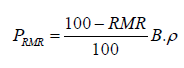 (6)
(6)
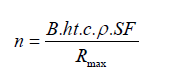 (7)
(7)
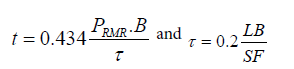 (8)
(8)
Where:
L = rock bolt length (m)
B = excavation width (m)
ESR = Excavation Support Ratio
n = number of rock bolt (pieces)
ht = rock-load height (m)
c = span excavation (m)
ρ= rock density (ton/m3)
SF = safety factor
Rmax = bearing capacity (ton)
LB = UCS shotcrete (ton/m2)
t =shotcrete thickness
τ =shotcrete shear stress (ton/m2)
PRMR = rock-load pressure (ton/m2)
Based on the equations above, the hanging wall with poor rock mass needs 16 rock bolts and only 12 rock bolts for fair rock mass. In additional, some rock bolt with grouted are also needed to support the systems. Eight grouted rock bolts and six grouted rock bolts are required for poor and fair rock masses, respectively. Shotcrete will be used as the support system. The capacity of shotcrete proposed around 25 MPa for all area withthe minimum thickness of shotcrete is 45 mm for hanging wall poor rock type and 35 mm for fair rock type.
However, the capacity of rock boltandshotcrete for hanging wall and footwall are identical, the numbers of rock bolt on footwall are less than the hanging wall due to the difference rock masses and rock properties. The numbers of rock bolt for footwall are 13 and 10 for fair and good rock mass, respectively. Six grouted rock bolts are needed for fair rock mass, and five grouted rock bolts for good rock mass. The thickness of shotcrete for fair rock mass in footwall is similar with shotcrete on hanging wall around 35 mm, and for good rock mass the thickness of shotcrete around 25 mm for the footwall.
In 2003, Wattimena, etalhasproposed a Hybrid Numerical-Empirical model to predict the support requirements in block caving mining method [7]. This model is the combination of numerical modeling and empirical analysis to design the support requirements. From numerical modeling, induced stress on complex design of mine method can be predicted, and the result is applied to the empirical Q system to design support system. To calculate the Q values as equation (1), induced stress is important as parameter for SRF. To describe SRF, Barton et al. [5] and Grimstad and Barton [6] proposed the relation between tangential induced stress and intact rock uniaxial strength [5,6]. Table 10 shows the classification of SRF, and the ratios between tangential stress and intact rock uniaxial strengthare given in Table 11.
| Description | σc/σ1 | σø/σc | SRF (Barton et al., 1974 Grimstad and Barton, 1993) |
|
| H | Low stress, near surface, open joints | >200 | <0.01 | 2.5 |
| J | Medium stress, favourable stress condition | 200-10 | 0.01-0.3 | 1 |
| K | High stress, very tight structure. Usually favourable to stability, may be unfavourable for wall stability | 10-5 | 0.3-0.4 | 0.5-2 |
| L | Moderate slabbing after > 1 hour in massive rock | 5-3 | 0.5-0.65 | 5-50 |
| M | Slabbing and rock burst after a few minutes in massive rock | 3-2 | 0.65-1 | 50-200 |
| N | Heavy rock burst and immediate dynamic deformations in massive rock | <2 | >1 | 200-400 |
Table 10: Classification of SRF parameter used in Q system (after Barton et al. [5] and Grimstad and Barton [6]).
| Position | Distance between HW decline to stope | Distance between FW decline to stope | |||||||||
| depth | 5 | 10 | 20 | 30 | 40 | 5 | 10 | 20 | 30 | 40 | |
| wall side | 88 | 0.13 | 0.10 | 0.09 | 0.09 | 0.09 | 0.08 | 0.05 | 0.05 | 0.04 | 0.04 |
| 150 | 0.22 | 0.18 | 0.16 | 0.15 | 0.15 | 0.13 | 0.09 | 0.08 | 0.07 | 0.07 | |
| 200 | 0.30 | 0.23 | 0.21 | 0.20 | 0.20 | 0.17 | 0.12 | 0.10 | 0.10 | 0.10 | |
| 300 | 0.45 | 0.35 | 0.31 | 0.30 | 0.30 | 0.25 | 0.17 | 0.15 | 0.15 | 0.15 | |
| roof | 88 | 0.22 | 0.24 | 0.26 | 0.26 | 0.26 | 0.12 | 0.12 | 0.12 | 0.12 | 0.12 |
| 150 | 0.40 | 0.42 | 0.45 | 0.47 | 0.45 | 0.21 | 0.21 | 0.22 | 0.22 | 0.23 | |
| 200 | 0.50 | 0.57 | 0.58 | 0.63 | 0.60 | 0.26 | 0.27 | 0.29 | 0.27 | 0.30 | |
| 300 | 0.77 | 0.86 | 0.85 | 0.92 | 0.95 | 0.42 | 0.42 | 0.41 | 0.42 | 0.45 | |
Table 11: Ratio between tangential stress and intact rock strength values.
By using Q system to design the underground support, the influence of induced stress on differentlevels can be predicted. Based on SRF values, we can obtain minimum and maximum range of SRF as input to calculate the Q values. Based on the values of ratio between tangential stress and intact rock strength, the research area could be classified into four classes of SRF. The classification of the SRF is given in Table 12. To determine Q values, other factorsas seen in Table 13 should be considered as well. The results of Q values are shown in Table 13.When the SRF classification of Barton et al. [5] and Grimstad and Barton [6] was applied, the range of Q values are 0.01 –2.04 and 0.02 – 3.06 (extremely poor to poor). Meanwhile, the Q values on footwall are higher than that on the hanging wall. The Q values are between 2.20–4.40 and 3.58 – 7.15 which mean poor to fair. Based on Table 13, it can be seen that the lowest Q values based on calculation using equation (1) is located on the roof. Therefore the roof condition will be considered to analyze the support requirements.
| σq/σc | SRF (Barton et al., 1974 Grimstad and Barton, 1993) |
Location |
| 0.04 – 0.3 | 1 | Hanging wall: Wallsides, depth 88 m- 200 m. Roof; depth 88 m. Footwall: Wallsides; all area. Roof; depth 88 m-200 m. |
| 0.3 – 0.47 | 0.5 – 2 | Hanging wall: Wallsides; depth 300 m. Roof; depth 150 m. Footwall: Roof, depth 300 m. |
| 0.5 – 0.63 | 5 – 50 | Hanging wall: Roof, depth 200 m |
| 0.77 – 0.95 | 50 – 200 | Hanging wall: Roof, depth 300 m |
Table 12: SRF classification.
| Location | chainage | RQD | Jn | Jr | Ja | Jw | Q values on depth (m) | |||
| 88 | 150 | 200 | 300 | |||||||
| Hanging wall | 565-568 | 55 | 9 | 2 | 6 | 1 | 2.04 | 1.02 | 0.04 | 0.01 |
| 591-593 | 55 | 12 | 2 | 3 | 1 | 3.06 | 1.53 | 0.06 | 0.02 | |
| Footwall | 791-792 | 60 | 9 | 3 | 3 | 0.66 | 4.40 | 4.40 | 4.40 | 2.20 |
| 814-817 | 65 | 6 | 3 | 3 | 0.66 | 7.15 | 7.15 | 7.15 | 3.58 | |
Table 13: Q values in the roof.
The Qvalue is then used to predict the supportsystem requirement. Two additional parameters should be considered in using the Q system for predicting the support systemfor an underground excavation are Excavation Support Ratio (ESR) and equivalent dimension.
Barton et al. [5] determined equivalent dimension (De) from the following equation:
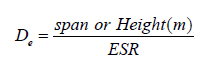 (9)
(9)
ESR values are taken as 1.60 for permanent decline, ramp, and shaft that are expected to serve for the whole production life of mine. The height of the hanging wall and the footwall declines are 4.8 m. The value of De is 3 m when the ESR for permanent decline.The support system can be determined by plotting the De values against Q that was proposed by Barton et al. [5]. The sample of the support requirement estimationis given in Figure 5.
For the hanging wall decline when the activities up to 88 m, the Q values are between 2.04–3.06. As a conservative approach, Q values of 2.04 is used to support system analysis. The support requires include shotcrete 4-5 cm thickness, and bolt with length 1.7 m and spacing 1.8 m. The support required will be increased with the increasing depth. This can be seen from the bolt spacing. For 150 m depth, the Q values are between 1.02-1.53. Within this range of Q value, the support system requires shotcrete with 4-5 cm thickness, and bolt with length 1.7m and spacing 1.7 m. The support system needs shotcrete 9-12 cm thickness, and bolt with length 1.7 m and spacing 1.2 m when at 200 m depth. The support system for activities up to 300 m needs rock bolt with 1.7 m length and 1.0 m spacing together with shotcrete 12-15 cm thickness.
For the footwall decline, the Q values are higher than that on the hanging wall decline. Similar with the hanging wall decline, the highest tangential stresses occur in the roof. The stress was observed to increase with increasing depth. For example, when the activities took place at depth ≤ 200 m, the Q value is estimated to be in the range of 4.40-7.15 and classified under faircategory. The proposed support system requiresbolt length 1.7 m with space 1.6 m. and shotcreteis not necessary. When the activities increase up to 300 m, the support system includes shotcrete 4-5 cm, bolt length 1.7 m and bolt space 1.8 m. Detail predicted supports are given in Table 14.
| Location | Support | Depth | ||||
| Ch. | 88 m | 150 m | 200 m | 300 m | ||
| Hanging wall | 565-568 | Rock bolt length | 1.7 m | 1.7 m | 1.7 m | 1.7 m |
| Bolt spacing | 1.6 m | 1.7 m | 1.2 m | 1.0 m | ||
| Shotcrete | unreinforced shotcrete, 40-50 mm | unreinforced shotcrete, 40-50 mm | fibre reinforced shotcrete, 50-90 mm | fibre reinforced shotcrete, 120-150 mm | ||
| 591-593 | Rock bolt length | 1.7 m | 1.7 m | 1.7 m | 1.7 m | |
| Bolt spacing | 1.4 m | 1.3 m | 1.2 m | 1.0 m | ||
| Shotcrete | unshotcrete | fibre reinforced shotcrete, 90-120 mm | fibre reinforced shotcrete, 50-90 mm | fibre reinforced shotcrete, 120-150 mm | ||
| Footwall | 791-792 | Rock bolt length | 1.7 m | 1.7 m | 1.7 m | 1.7 m |
| Bolt spacing | 1.6 m | 1.6 m | 1.6 m | 1.4 m | ||
| Shotcrete | unshotcrete | unshotcrete | Unshotcrete | unshotcrete | ||
| 814-817 | Rock bolt length | 1.7 m | 1.7 m | 1.7 m | 1.7 m | |
| Bolt spacing | 1.5 m | 1.5 m | 1.5 m | 1.4 m | ||
| Shotcrete | unshotcrete | unshotcrete | Unshotcrete | unshotcrete | ||
Table 14: Support system recommended based on Q system.
Recommended support systems for different levels (88 m, 150 m, 200 m and 300 m depth) were designed using a new method; Hybrid Numerical Empirical Model.
The following results were obtained from damage potential analysis. Damage potential will increase with increasingthedepth. Low to moderate rock spalling will occur for hanging wall on 150-200 m depth in the roof, and there will be high rock spalling when the mine activities below 300 m depth. In contrast, footwall will start encounter low rock spalling when the activities below 300 m.
It was recommended by the RMR system classification to use rock bolts and shotcrete. In hanging wall decline, minimum rock bolts for poor rock mass are 16 pieces and8 pieces of rock bolts grouted. The shotcrete is required for this condition with minimum thickness is recommended 45 mm and the capacity minimum 25 MPa. However, footwall classified as good rock mass, the support system is needed. For the good condition of rock mass 10 pieces of rock bolt and 5 pieces of rock bolt grouted are required with minimum 25 mm thickness of shotcrete.
Based on Qsystem, which is analysed by using Hybrid Numerical Empirical Model the requirement of rock bolts length aresame for all rock mass classifications that are 1.7 m. Recommendedsupport system by Q classification influenced by depth. The shotcrete will be thicker and rock bolt space more closely as increasing the depth. When the activities at 88 m depth, the support system requires shotcrete 4 – 5 cm thickness and bolt spacing 1.8 m.Meanwhile, the shotcrete is 12 – 15 cm thickness and bolt spacing is 1.0 m are required for depth up to 300 m. From this study the advantage to calculate support requirements using SRF is influence of induced on different levels could be predicted.
The authors would like to acknowledge PT. CibaliungSumberdaya management for the opportunity to conduct our research and great appreciate to SusenoKramadibrata for the support to use facility in Geomechanics Laboratory, Department of Mining Engineering ITB. The first author also would like to thank to DIKTI Indonesia to support the scholarship.