Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2016) Volume 6, Issue 4
The aim of this paper was to clarify the relationship between subjective preference for air-conditioner sounds and sound quality indices, such as factors extracted from the autocorrelation function (ACF) inside a car in summer and winter. We evaluated subjective preference using a paired comparison method. Specifically, we performed multiple regression analyses with scale values of preference as the outcome variable using a linear combination of LAeq, the ACF factors, and their standard deviations. The results indicated that total subjective preference for air-conditioner sound can be predicted using LAeq, the amplitude of the first maximum peak of the ACF, φ1, which corresponds to the pitch strength, and the width of the first decay of the ACF, Wφ(0), which corresponds to the spectral centroid. We found preference to increase with a decrease in LAeq and φ1, and an increase in Wφ(0). Thus, air-conditioner sounds with quieter levels, weaker pitch strength, and lower spectral centroid were associated with higher levels of preference. The temperature of the atmosphere had no effect on subjective preference for air-conditioner sounds.
Keywords: Air-conditioner sound; Autocorrelation function; Spectral centroid; Pitch strength
The sound quality inside a car is a very important aspect of automobile design. Many different sources produce sounds that can be heard inside a car. Previous studies have investigated the sound quality of the sources, such as those produced by the engine [1,2], door closing [3,4], and power windows [5,6]. Recent developments in vehicle design have led to a reduction in various sound levels, principally those produced by the engine. Thus, the contribution pattern of sound sources to the overall interior sound inside a car has changed. Previously masked sound sources, such as those produced by the airconditioner, have become noticeable to passengers, and are therefore playing a heightened role in passenger comfort.
Several studies have evaluated the relationships between objective sound quality metrics (termed psychoacoustic factors) such as loudness, sharpness, and roughness [7] and subjective factors such as similarity, annoyance, and pleasantness for air-conditioner sounds [8,9]. The results indicated that psychoacoustic factors can influence subjective responses. As with other psychoacoustic factors, autocorrelation function (ACF) factors are significantly correlated with subjective responses [10]. In this study, we address the ACF factors implicated in the evaluation of air-conditioner sound quality to clarify the parameters that most strongly influence subjective responses to airconditioner sounds. One rationale for the ACF approach is that the perception of the quality of most sounds is based on information that is embedded in the timing of the spikes in the sound, i.e., the temporal correlation representations arise from spike timing patterns in the auditory nerve, and this is reflected in the ACF of the sound [11,12]. Another rationale is that the ACF factors describe the basic temporal sensations, such as pitch, loudness, or timbre [13,14]. In addition, ACF analysis is simple compared with psychoacoustic indices, which require complex calculations [7].
Air-conditioning systems provide thermal comfort by controlling the temperature of the atmosphere. Previous studies have indicated that air-conditioner sounds influence thermal perception due to the interaction between acoustic and thermal perception [15,16]. Therefore, the temperature of the atmosphere may affect sound quality evaluations. However, previous studies have not considered the interaction between acoustic and thermal perception [8,9].
The purposes of this study were to 1) clarify the dominant factors that modulate subjective preference for air-conditioner sound and 2) evaluate the effects of atmospheric temperature on subjective preference for air-conditioner sound. We considered subjective preference as an overall subjective impression of sound and ACF factors as sound quality indices.
Analysis of air-conditioner sounds
We made recordings of air-conditioner sounds in two different cars (A and B). The car windows and doors were always closed and the airconditioning system was operated with the car engine off during the recording. While not simulating actual driving conditions, these test conditions eliminated possible effects of noise from the engine and road conditions on subjective preference for air-conditioner sounds. The effects of these other noises will be examined in future experiments. The air-conditioning systems in the cars under investigation had three air outlets, here called Face, Foot, and Def. Face and Foot modes allow the air to flow to the driver’s face and feet, respectively. Def mode enables the air to flow to the windshield to defrost the glass. An omnidirectional microphone was placed at ear height with respect to the driver’s sitting position. A driver always occupied the driver seat, but fellow passengers were not always in other seats. The focus was on the effects of the sound source, not the position of the listener; thus, the microphone was only set toward the driver’s position. For all measurements, the sound was recorded via an analog-to-digital/digital-to-analog (AD/DA) converter at a sampling rate of 48 kHz and with a sampling resolution of 16 bits. The fan speed of the air-conditioning system was set to the highest of multiple fan speeds during sound recordings for the subjective preference test. We used the recorded sounds from car A in the Face, Foot, and Def modes and those from car B in the Face and Foot modes for the preference test.
In addition to the real sounds recorded in the car, we generated simplified modeled sounds for the preference test. We estimated the spectral envelope of the recorded sound from car B in the Face mode via 150th order linear predictive coding. We produced five modeled sounds by stretching the envelope by 1/2, 2/3, 1, 3/2, and 2 times in the frequency domain [16].
Sound quality evaluation has focused on psychoacoustic factors including loudness, sharpness, roughness, and fluctuation strength [7]. Loudness is the psychological counterpart to the physical strength of a sound. In this study, we considered non-stationary time-varying loudness [17]. Sharpness is a measure of the high frequency content of a sound, where a higher proportion of high frequency components indicates a sharper sound. The sharpness of a sound can be calculated via the addition of a weighting function to its specific loudness spectrum [7]. Roughness quantifies the subjective perception of the rapid (15-300 Hz) amplitude modulation of a sound. Roughness is generally calculated using the time-varying loudness multi-spectrum. For this study, we used a modified version of the roughness calculation [18]. We evaluated fluctuation strength, which is similar in principle to roughness, but reflects the subjective perception of the slower (at frequencies up to 20 Hz) amplitude modulation of a sound. The sensation corresponding to fluctuation strength persists for the sound components up to 20 Hz, where roughness dominates for the higher frequencies. Fluctuation strength is also calculated using the timevarying non-stationary loudness multi-spectrum [7]. We calculated the loudness, sharpness, roughness, and fluctuation strength for real and modeled air-conditioner sounds. The size of the temporal window used for analysis was 0.5 s. Analyses were conducted using a MATLABbased analysis program.
The ACF factors for sound quality evaluation have been previously proposed [13,14]. To calculate the ACF factors, the normalized ACF of the signal recorded from microphones, p(t), as a function of the running step, s, is defined by
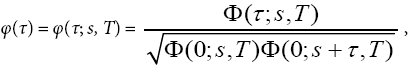 (1)
(1)
Where
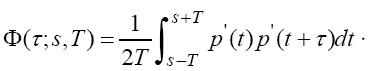 (2)
(2)
Here, 2T is the integration interval and p’(t) = p(t)*se(t), where se(t) is the ear sensitivity. In this study, p(t) is the signal that was measured using an omnidirectional microphone. se(t) represents the impulse response of an A-weighted network, including the transfer functions of the human outer and middle ear, for convenience [13,14]. Normalization of the ACF is performed using the geometric mean of the energy at s and the energy at s+τ, and should not be carried out based on the energy at s alone; this ensures that the normalized ACF satisfies the condition 0 ≤ φlr(τ) ≤ 1.
LAeq is determined based on the A-weighted p(t) signal as a function of s. LAeq is then calculated using
LAeq (s,T) =10logΦ(0;s,T) . (3)
This means that the ACF includes LAeq as a factor. The other ACF factors are calculated from the normalized ACF. τ1 and φ1 are defined as the time delay and the amplitude of the first maximum peak as shown in Figure 1(a). τ1 and φ1 are related to the perceived pitch and the pitch strength of the complex sounds, respectively [13,19]. Figure 1 (b) shows the ACFs for a 500 Hz pure tone, the 1/3 and 1/1 octave band noises at a center frequency of 500 Hz, and the 1/1 octave band noise at a center frequency of 1 kHz. Sounds with a low center frequency have larger τ1 values. In contrast, sounds with wide bandwidths have a lower φ1 value. Therefore, higher values of τ1 and φ1 indicate that the sound has a lower pitch and a stronger pitch, respectively. The other ACF factor, Wφ(0), is defined using the delay time interval at a normalized ACF value of 0.5, as shown in Figure 1(a), and represents the width of the first decay. Wφ(0) is equivalent to the spectral centroid because the correlation coefficient between Wφ(0) and the spectral centroid when calculated from a pure tone, the 1/1 and 1/3 octave band noises, the white noise, and the pink noise, is 0.98 [14]. The 1/1 octave band noise at a center frequency of 1 kHz has a smaller Wφ(0) than that at a center frequency of 500 Hz, as shown in Figure 1(b). Higher values of Wφ(0) indicate that the sound includes a higher proportion of low frequency components. We calculated the τ1, φ1, and Wφ(0) for real and modeled air-conditioner sounds as a function of time. The integration interval was 2T = 0.5 s and the running step was s = 0.1 s in all calculations. The analyses were conducted using a MATLAB-based analysis program.
Subjective preference tests
To clarify the effects of the sound quality indices on preference, we evaluated subjective preference for air-conditioner sounds. In summer, 12 and 11 participants took part in the experiment for real and modeled sounds, respectively. In winter, 10 participants took part in the experiment for both real and modeled sounds. All participants had normal hearing, no history of neurological disease, and ranged in age between 20 and 40 years. Informed consent was obtained from each participant after the nature of the study had been explained. The study was approved by the ethics committee of the National Institute of Advanced Industrial Science and Technology (AIST) of Japan.
We used five real and five modeled air-conditioner sounds as the sound sources. The experiment was carried out separately for real and modeled sounds. The monaural signal recorded by the omnidirectional microphone or the model of the recorded signal was presented binaurally through headphones (HD650, Sennheiser) in a soundproof room. Five real and five modeled sounds were presented at A-weighted equivalent sound pressure level (SPL), denoted by LAeq, of 50, 60, and 70 dBA. LAeq was verified using a dummy head microphone (KU100, Neumann) and a sound calibrator (Type 4231, B&K). In total, 15 different sound stimuli were presented in each experiment for real and modeled sounds. The air temperature of the room was 25 ± 1 and 21 ± 1 degrees in summer and winter, respectively.
We performed Scheffé’s paired comparison tests [20] for all combinations of sound pairs (i.e., 210 pairs (N(N−1), N = 15)) by interchanging the order of the pairs. The pairs were presented in random order. The durations of the sound stimuli were 2000 ms, the rise and fall times were 100 ms, and the silent interval between sounds was 1000 ms. after the presentation of each pair of sounds, the participants were required to compare the two sounds by considering the differences between the two sounds. The participants evaluated the sound differences on a five-point scale, from 1 for most preferred to 5 for least preferred. The approximate duration of the experiment was 25 minutes. Regarding subjective preference, Scheffé’s paired comparison method is useful because it lets participants simply judge which and how much of the sounds they prefer to hear.
The averaged scale values of preference for each participant were calculated based on the modified Scheffé’s method [21]. We then conducted an analysis of variance (ANOVA) for the results of the paired comparison experiments. To calculate the effects of each objective factor on participant preference, we conducted multiple regression analyses with the scale values of preference as the outcome variable. In model 1, we used a linear combination of loudness, sharpness, roughness, fluctuation strength, and their standard deviations (SDs) as predictive variables in a stepwise fashion. The predictive variables in model 2 were the LAeq, the ACF factors, and their SDs. The analyses were carried out using SPSS statistical analysis software (SPSS version 22.0, IBM).
Subjective preference tests for real air-conditioner sounds
The ANOVA for the scale values of preference revealed that the primary effect (i.e., the differences between the air-conditioner sounds) was statistically significant in summer (F(14, 2249) = 300.62, p < 0.01) and winter (F(14, 1859) = 285.86, p < 0.01). We found a statistically significant interaction between the primary effect and the participant in summer (F(154, 2249) = 9.42, p < 0.01) and winter (F(126, 1859) = 9.42, p < 0.01). Table 1 shows the ANOVA results for scale values of preference for real air-conditioner sounds. The averaged scale values of preference for all participants in summer and winter are shown as a function of Wφ(0) in Figure 2.
| (a) Factors | Deviation | Degrees of freedom | Biased deviation | F0 | F1% |
| Stimuli | 3182.96 | 14 | 227.35 | 300.62 | 2.09 |
| Stimuli ´ participants | 1097.58 | 154 | 7.13 | 9.42 | 1.29 |
| Combination | 99.75 | 91 | 1.10 | 1.45 | 1.40 |
| Order | 1.68 | 1 | 1.68 | 2.22 | 6.65 |
| Order ´ participants | 38.16 | 11 | 3.47 | 4.58 | 2.26 |
| Residual | 1700.88 | 2249 | 0.76 | ||
| Overall result | 6121 | 2520 | |||
| (b) Factors | Deviation | Degrees of freedom | Biased deviation | F0 | F1% |
| Stimuli | 3382.87 | 14 | 241.63 | 285.86 | 2.09 |
| Stimuli ´ participants | 1003.26 | 126 | 7.96 | 9.42 | 1.33 |
| Combination | 106.98 | 91 | 1.18 | 1.39 | 1.39 |
| Order | 3.28 | 1 | 3.28 | 3.88 | 6.65 |
| Order ´ participants | 37.24 | 9 | 4.14 | 4.89 | 2.42 |
| Residual | 1571.37 | 1859 | 0.85 | ||
| Overall result | 6105 | 2100 |
Table 1: Analysis of variance for real air-conditioner sounds in (1a) summer and (1b) winter.
We performed multiple linear regression analyses with the psychoacoustic factors as the explanatory variable. The final version of model 1 indicated that loudness and sharpness were significant factors in summer, while loudness and fluctuation strength were significant factors in winter:
SVpreference in summer ≈ a1*loudness + a2*sharpness + c1, (4)
SVpreference in summer ≈ a3*loudness + a4*fluctuation strength + c2. (5)
The model was statistically significant for the summer experiment (F(2, 177) = 297.2, p < 0.01), and the modified determination coefficient was 0.87. The standardized partial regression coefficients of the variables a1 and a2 in Equation (4) were −0.83 and −0.17. The model was also statistically significant for the winter experiment (F(2, 147) = 237.83, p < 0.01), and the modified determination coefficient was 0.87. The standardized partial regression coefficients of the variables a3 and a4 in Equation (5) were −0.67 and −0.25.
We also performed multiple linear regression analyses with the ACF factors as the explanatory variable. The final version of model 2 indicated that LAeq, φ1, and Wφ(0) were significant factors in summer and winter:
SVpreference in summer ≈ b1*LAeq + b2*φ1 + b3*Wφ(0) + d1, (6)
SVpreference in summer ≈ b4*LAeq + b5*φ1 + b6*Wφ(0)+ d2. (7)
The model was statistically significant for the summer experiment (F(3, 176) = 190.63, p < 0.01) and the modified determination coefficient was 0.87. The standardized partial regression coefficients of the variables b1, b2, and b3 in Equation (6) were −0.83, −0.14, and 0.12, respectively. The model was also statistically significant for the winter experiment (F(3, 146) = 158.23, p < 0.01) and the modified determination coefficient was 0.88. The standardized partial regression coefficients of the variables b4, b5, and b6 in Equation (7) were −0.85, −0.13, and 0.13, respectively.
In a similar manner, we predicted the scale values of preference for each participant via multiple regression analysis. Because the explanatory powers of models 1 and 2 were nearly identical, we show the results produced using ACF factors only to focus on the effects of the ACF factors on preference. The significant factors, the standardized regression coefficients, and the correlation coefficients between the measured and calculated scale values of preference in summer and winter are listed in Tables 2 and 3. LAeq was the most significant factor for all participants in summer and winter. The standardized partial regression coefficients were negative for all participants, with the exception of one each in the summer and winter experiments. Wφ(0) and φ1 were significant factors for seven and five of the 12 participants in summer and six and five of the 10 participants in winter. The standardized partial regression coefficients for Wφ(0) and φ1 were positive and negative, respectively.
| Participant | Factor 1 | Factor 2 | Factor 3 | r |
|---|---|---|---|---|
| A | LAeq** -0.93 | φ1* -0.19 | Wφ(0)* 0.17 | 0.99 |
| B | LAeq** -0.95 | 0.95 | ||
| C | LAeq** -0.89 | Wφ(0)** 0.37 | 0.96 | |
| D | LAeq** -0.99 | 0.99 | ||
| E | LAeq** -0.99 | Wφ(0)* 0.09 | 0.99 | |
| F | LAeq** -0.94 | φ1** -0.30 | 0.99 | |
| G | LAeq ** -0.97 | 0.97 | ||
| H | LAeq** -0.97 | φ1** -0.14 | Wφ(0)* 0.09 | 0.99 |
| I | LAeq** 0.79 | Wφ(0)** 0.47 | 0.92 | |
| J | LAeq** -0.95 | Wφ(0)* 0.148 | 0.97 | |
| K | LAeq** -0.93 | φ1* -0.35 | 0.99 | |
| L | LAeq** -0.88 | φ1** -0.28 | Wφ(0)* 0.20 | 0.99 |
Table 2: Individual results for the significant factors, standardized regression coefficients, and correlation coefficients between the measured and calculated scale values of preference for real air-conditioner sounds in summer. Asterisks represent the level of significance, i.e., ** p < 0.01, * p < 0.05.
| Participant | Factor 1 | Factor 2 | Factor 3 | r |
|---|---|---|---|---|
| A | LAeq** -0.99 | Wφ(0)** 0.38 | Wφ(0)_SD* -0.14 | 0.99 |
| B | LAeq** -1.01 | φ1_SD** -0.17 | 0.99 | |
| C | LAeq** -1.01 | Wφ(0)** 0.21 | Wφ(0)_SD** -0.10 | 0.99 |
| D | LAeq** -0.96 | Wφ(0)** 0.32 | Wφ(0)_SD* -0.19 | 0.98 |
| E | LAeq** -0.97 | φ1* -0.16 | 0.98 | |
| F | LAeq** -0.91 | Wφ(0)** 0.26 | φ1* -0.18 | 0.98 |
| G | LAeq ** -0.98 | φ1** -0.16 | 0.99 | |
| H | LAeq** -0.93 | Wφ(0)** 0.27 | φ1* -0.12 | 0.99 |
| I | LAeq** 0.72 | 0.72 | ||
| J | LAeq ** -0.91 | φ1** -0.25 | Wφ(0)** 0.20 | 0.99 |
Table 3: Individual results for the significant factors, standardized regression coefficients, and correlation coefficients between the measured and calculated scale values of preference for real air-conditioner sounds in winter. Asterisks represent the level of significance, i.e., ** p < 0.01, * p < 0.05.
Subjective preference tests for modeled air-conditioner sounds
The ANOVA for the scale value of preference revealed that the primary effect (i.e., the differences between the stimuli) was statistically significant in summer (F(14, 2054) = 877.00, p < 0.01) and winter (F(14, 1859) = 225.94, p < 0.01). We found a statistically significant interaction between the primary effect and the participant in summer (F(140, 2054) = 9.27, p < 0.01) and winter (F(126, 1859) = 11.54, p < 0.01). Table 4 shows the ANOVA results for scale values of preference for modeled air-conditioner sounds. The averaged scale values of preference for all participants in summer and winter are shown as a function of Wφ(0) in Figures 3.
| (a) Factors | Deviation | Degrees of freedom | Biased deviation | F0 | F1% |
| Stimuli | 3700.62 | 14 | 264.33 | 877.00 | 2.09 |
| Stimuli ´ participants | 391.10 | 140 | 2.79 | 9.27 | 1.31 |
| Combination | 60.99 | 91 | 0.67 | 2.22 | 1.39 |
| Order | 0.14 | 1 | 0.14 | 0.47 | 6.65 |
| Order ´ participants | 13.07 | 10 | 1.31 | 4.34 | 2.33 |
| Residual | 619.08 | 2054 | 0.30 | ||
| Overall result | 4785 | 2310 | |||
| (b) Factors | Deviation | Degrees of freedom | Biased deviation | F0 | F1% |
| Stimuli | 3014.57 | 14 | 215.33 | 225.94 | 2.09 |
| Stimuli ´ participants | 1453.77 | 126 | 11.54 | 12.11 | 1.33 |
| Combination | 127.58 | 91 | 1.40 | 1.47 | 1.39 |
| Order | 6.08 | 1 | 6.08 | 6.38 | 6.65 |
| Order ´ participants | 47.35 | 9 | 5.26 | 5.52 | 2.42 |
| Residual | 1771.65 | 1859 | 0.95 | ||
| Overall result | 6421 | 2100 |
Table 4: Analysis of variance for modeled air-conditioner sounds in (a) summer and (b) winter.
We performed multiple linear regression analyses with the scale values of preference for all participants as the outcome variable and psychoacoustic factors as the explanatory variable. The final version of model 1 indicated that loudness and sharpness were significant factors in summer and winter:
SVpreference in summer ≈ e1*loudness + e2*sharpness + g1, (8)
SVpreference in summer ≈ e3*loudness + e4*sharpness + g2. (9)
The model was statistically significant for the summer experiment (F(2, 162) = 631.40, p < 0.01), and the modified determination coefficient was 0.94. The standardized partial regression coefficients of the variables e1 and e2 in Equation (8) were −0.92 and −0.12. The model was statistically significant for the winter experiment (F(2, 147) = 140.31, p < 0.01), and the modified determination coefficient was 0.81. The standardized partial regression coefficients of the variables e3 and e4 in Equation (9) were −0.79 and −0.10.
We performed multiple linear regression analyses with the scale values of preference for all participants as the outcome variable and ACF factors as the explanatory variable. The final version of model 2 indicated that the LAeq and Wφ(0) were significant factors in summer and the LAeq and the SD of Wφ(0) were significant factors in winter:
SVpreference in summer ≈ f1*LAeq + f2*Wφ(0) + g3, (10)
SVpreference in summer ≈ f3*LAeq + f4*SD_Wφ(0) + g4. (11)
The model was statistically significant for the summer experiment (F(2, 162) = 732.55, p < 0.01) and the modified determination coefficient was 0.95. The standardized partial regression coefficients of the variables f1 and f2 in Equation (10) were −0.99 and 0.11. The model was statistically significant in the winter experiment (F(2, 147) = 148.37, p < 0.01) and the modified determination coefficient was 0.82. The standardized partial regression coefficients of the variables f3, and f4 in Equation (11) were −0.82 and 0.10.
As in the case with real air-conditioner sounds, we show only the results of the multiple regression analysis for the scale values of preference for each participant produced using ACF factors. The significant factors, the standardized regression coefficients, and the correlation coefficients between the measured and calculated scale values of preference in summer and winter are listed in Tables 5 and 6. LAeq was the most significant factor for all participants with the exception of one. In the summer experiment, the standardized partial regression coefficients were negative for all participants except one. Additionally, Wφ(0) and the SD of Wφ(0) were significant factors for three of the eleven participants. The standardized partial regression coefficients for Wφ(0) and the SD of Wφ(0) were all positive. In the winter experiment, the SD of Wφ(0) was the significant factor for 6 of the 10 participants. The standardized partial regression coefficients for the SD of Wφ(0) were positive for all except one participant.
| Participant | Factor 1 | Factor 2 | Factor 3 | r |
|---|---|---|---|---|
| A | LAeq** -0.98 | 0.98 | ||
| B | LAeq** -0.98 | Wφ(0)** 0.14 | Τ1* 0.06 | 0.99 |
| C | LAeq** -0.99 | 0.99 | ||
| D | LAeq** -0.98 | 0.98 | ||
| E | LAeq** -0.99 | 0.99 | ||
| F | LAeq** -0.91 | Wφ(0)** 0.41 | φ1_SD** 0.18 | 0.99 |
| G | LAeq** -0.97 | Wφ(0)_SD ** 0.19 | 0.98 | |
| H | LAeq** -0.99 | t1_SD ** 0.13 | LAeq_SD* 0.08 | 0.99 |
| I | LAeq** -0.97 | Wφ(0)_SD** 0.15 | 0.99 | |
| J | LAeq** -0.97 | Wφ(0)* 0.13 | 0.98 | |
| K | LAeq** -0.97 | Wφ(0)_SD* 0.13 | 0.99 |
Table 5: Individual results for the significant factors, standardized regression coefficients, and correlation coefficients between the measured and calculated scale values of preference for modeled air-conditioner sounds in summer. Asterisks represent the level of significance, i.e., ** p < 0.01, * p < 0.05.
| Participant | Factor 1 | Factor 2 | Factor 3 | r |
|---|---|---|---|---|
| A | LAeq** -0.95 | Wφ(0)_SD** 0.31 | 0.98 | |
| B | LAeq** -0.99 | Wφ(0)** 0.16 | Τ1_SD* 0.10 | 0.99 |
| C | LAeq** -0.99 | Wφ(0)_SD* 0.11 | 0.99 | |
| D | LAeq** -0.97 | Wφ(0)_SD** 0.20 | LAeq_SD* -0.11 | 0.99 |
| E | LAeq** -0.99 | 0.99 | ||
| F | LAeq** -0.98 | Wφ(0)_SD** 0.22 | 0.99 | |
| G | LAeq** -0.99 | 0.99 | ||
| H | LAeq** -0.98 | Wφ(0)_SD** 0.16 | 0.99 | |
| I | Wφ(0)_SD** -0.67 | LAeq** 0.49 | 0.83 | |
| J | LAeq** -0.97 | Τ1** 0.18 | Τ1_SD* -0.12 | 0.99 |
Table 6: Individual results for the significant factors, standardized regression coefficients, and correlation coefficients between the measured and calculated scale values of preference for modeled air-conditioner sounds in winter. Asterisks represent the level of significance, i.e., ** p < 0.01, * p < 0.05.
In this study, we investigated relationships between subjective preference for real and modeled air-conditioner sounds and sound quality indices. We found subjective preference to increase with decreasing LAeq and loudness. This was likely because the airconditioner sounds were presented at LAeqs, of 50, 60, and 70 dBA; the differences between these values were sufficiently large to be noticeable by the participant.
As for ACF factors, Wφ(0) had a significant effect on subjective preference for all air-conditioner sounds except for the modeled sounds in winter, although the SD of Wφ(0) had a significant effect on subjective preference for modeled air-conditioner sounds in winter. The correlation coefficients between preference and Wφ(0) were positive, suggesting that the air-conditioner sounds with lower spectral centroids were more strongly preferred. Previous studies have indicated that Wφ(0) is significantly and negatively correlated with subjective annoyance for noises in a train car [22] and station [23]. This indicates that noises with lower spectral centroids are less annoying, consistent with the present findings.
Another ACF factor, φ1, also had a significant effect on subjective preference for real air-conditioner sounds. The correlation coefficients between preference and φ1 were negative, suggesting that the airconditioner sounds with lower strength of pitch were more strongly preferred. A previous study indicated a positive relationship between subjective preference for birdsongs and φ1 [14]. This is not consistent with the present findings. This difference may be due to the tonal components of birdsongs, while air-conditioner sounds have no such components. Additionally, for refrigerator noise, φ1 has a positive effect on subjective noisiness, meaning that noises with a lower strength of pitch are perceived as less noisy [10]. This is consistent with the present results. In the case of modeled air-conditioned sounds, φ1 had no significant effect on preference. This may be due to the smaller size of the variation in φ1 values for the modeled sounds compared with that for the real sounds.
Sounds that air-conditioner systems generate are typically regarded as unwanted noise. Our results indicated that listeners preferred certain types of air-conditioner sounds. This suggests that modifying these sounds can improve in-car sound quality. Additionally, because ACF factors calculated from air-conditioner sounds predict subjective preference for the sounds, ACF factors can also rank the quality of the sounds and provide clues for how to modify them.
Air-conditioner sounds affect thermal perception [15,16], although our results indicated that the temperature of the atmosphere did not influence subjective preference for the sounds. Because ACF factors calculated from air-conditioner sounds predict subjective preference for the sounds, ACF factors can also predict thermal perception affected by these sounds. This means quantification of air-conditioner sounds by ACF factors could be helpful for improving not only acoustic but also perceived thermal environments inside cars.
We analyzed the relationship between subjective preference for air-conditioner sounds and sound quality indices, such as ACF factors. The results indicated that the LAeq, φ1, and Wφ(0) were significantly influential factors in the subjective preference for air-conditioner sounds. Lower LAeq and φ1 were associated with higher preference, meaning that air-conditioner sounds with lower sound pressure levels and weaker pitch strength are more strongly preferred. Higher Wφ(0) led to higher preference, meaning that air-conditioner sounds with lower spectral centroids are more strongly preferred. When we controlled for temperature, the results were not influenced by the temperature of the atmosphere.
This work was partly supported by a Grant-in-Aid for Scientific Research (B) (Grant No. 15H02771 and 26282130) from the Japan Society for the Promotion of Science.