International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2016) Volume 7, Issue 4
In this paper, moment-curvature behavior of reinforced concrete column with constant axial load is determined using finite element method and then it is introduced to a single degree of freedom (SDOF) model based on Euler- Bernoulli theory. Using this SDOF model, dynamic response of the RC column under the blast loading is estimated. The introduced SDOF includes secondary moments (P-δ) effects, nonlinear behavior of the material and effects of strain rate on concrete and steel materials through the time calculation of the model. Results obtained from SDOF model for transverse displacement of RC column under blast loading is compared to analysis by finite element software OPENSEES. Then, introduced SDOF method is used for drawing Pressure-Impulse (P-I) diagram of the column with considering the presence of axial compressive load. According to the results, introduced SDOF model has simple and quick computations and accuracy of predictions is acceptable.
<Keywords: Blast loading; Equivalent single degree of freedom; Pressure-impulse diagram; RC columns
In order to analyze structural elements under blast loading there are two common methods include single degree of freedom (SDOF) method and finite element method (FEM). The SDOF method is a simple approach with acceptable precision and is the basis of many references of analysis and design of structures under blast and explosion [1-5]. In the conducted studies it has been shown that equivalent SDOF system can model the behavior of steel beams and columns [6-9], slabs and walls [10-12] and reinforced concrete beams [13-16] under blast loading with acceptable accuracy. The SDOF method for modeling the response of retrofitted structural members in the face of blast has also been used [17,18]. When a column is under simultaneous effect of axial force and lateral load, the existence axial load due to P-δ effects, could change the affecting moments on the column. The studies on how to insert the P-δ effects in SDOF models for columns under blast loading is very rare. Nassr et al. have examined the axial load effect in SDOF model of thin steel columns under blast [6]. Some studies have also been conducted by engineering community of USA army that publishing the complete results of these studies has legal and military constraints [19,20]. Using SDOF method, the Pressure-Impulse (P-I) diagrams can be extracted for various structural members. P-I diagram is a graphical tool for assessment and preliminary design of structures and structural members under blast loads [21-27]. With drawing P-I diagram for a structure, a comprehensive and rapid description of structural response and the amount of damage suffered can be provided. Figure 1 shows normalized (dimensionless) P-I diagram for an ideal SDOF system without damping under positive phase of blast pressure. In this case, blast load parameters are relative to the structural dynamic response parameters, such as mass and dynamic capacity of member, to determine the normalized P-I diagram for the structural member [25]. Points in the left side and bottom of the curve represent the states that do not reach the target level of damage and points in the right side and top of the charts represent the points that cause damage more than target level of damage. A more detailed description of the parameters used in Figure 1 and how to calculate them are given in Section 7 in this paper.
P-I diagrams can be prepared with different analytical, numerical and experimental ways [22,25,27-31]. Experimental tests for blast loading are expensive, very difficult and have legal and military limits. Using finite elements software packages the different response modes,P-δ effects and overall and local damages and their impact on the P-I diagram can be evaluated. However, this method due to the high complexity, high time of calculations and the need to have enough skills and experience of using software, for extensive parametric studies isn’t very appropriate.
In this paper, the flexural behavior (moment-curvature) of a reinforced concrete column section using finite element software of open system for earthquake engineering simulation (OpenSees) has been determined and introduced to the calculation of SDOF analytical model in order to estimate transverse displacement response of column under simultaneous compressive axial force and lateral loading of blast. The SDOF introduced model includes the effects of secondary moments (P-δ) and also the effects of high strain rates on the behavior specifications of concrete and steel rebar. In this method, to consider the effects of the existence of column axial loading (P-δ) the concept of reduced resistance function is used. Using the introduced process, P-I dimensionless curves have been plotted for reinforced concrete column.
Figure 2 shows the distribution of stress and strain in the rectangular RC section at the ultimate state. Strain distribution in the height of the section has been assumed to be linear and curvature of section (θ) is equal to the slope of this line. Also, the tensile strength of concrete has been ignored.
In the figure above, fyk is the yield stress of reinforcement steel, fcu is the ultimate strength of concrete, εcu is the ultimate strain of concrete, xu is the depth of neutral axis in the ultimate state, b is the width, h is the height and d is effective depth of the section. Here, the ultimate state is defined as reaching concrete strain to its maximum amount εcu. By writing the equation of moment equilibrium around the plastic center of section according to Equation 1, the neutral axis height at the ultimate state (Xu) was obtained and replacing it in the Equation 2 the ultimate axial load (Nu) of the section can be determined. In fact, the Equation 2 is the equation of horizontal force equilibrium in the section.
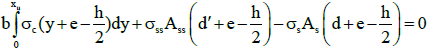 (1)
(1)
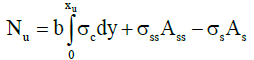 (2)
(2)
In the above equations, ss subtitle is related to reinforcement in the face subjected to blast, s is the reinforcement in the face of behind the blast pressure and c is the concrete.
The analysis of single degree of freedom is an essential part of blast engineering and the reason of its popularity is no need to specialized finite element software [8]. In this method the structural member is idealized as an equivalent mass-spring system with one degree of freedom. Structural response history under blast loading is often determined by numerical integration of equation of motion for equivalent system. The equivalent SDOF parameters are calculated using the principle of energy balance. This means that at any time, the Kinetic energy in equivalent mass, internal strain energy in equivalent strength and external work in equivalent load should be the same in the real continuous member.
The available approximations of the SDOF is based on the assumption that structure experience a deformation pattern that is described with only one parameter. In the other words, equating the energy on the basis of a specific deformation state is taken place and often deformation form of structure under static load is the best possible approximation [10]. In order to consider the states of plastic deformation, different equating coefficients for elastic and plastic states are used. Because in the continuous real elements due to plasticizing some of sections, the stiffness and resistance is changed compared to elastic mode. To ensure that response parameters which are obtained from SDOF system have sufficient accuracy, this equivalent SDOF is selected in such a way that the maximum deformation corresponds the deformation of a critical point in the actual structure [32]. SDOF classical theory which is used in blast engineering, is according to Biggs method in which a mass-spring equivalent system is determined for a actual structure with distributed loading [32].
Consider a two ends hinged member under distributed uniform load. As an estimation of elastic deformation of member under mentioned load, the static deformed shape of simple beam under uniform load can be applied [32] (Equation 3). In Equation 3, l is the length of member and x is the non-deformed longitudinal axis. In plastic range, it is assumed that a plastic hinge is formed in the middle of the member height; so the deformed mode is linear (Equation 3- b).
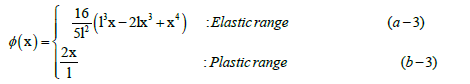 (3)
(3)
With an overview of the research findings it can be found that various damping ratios in the range of 0 to 5% have been used for the analysis of SDOF under blast loads [13-15]. It has been shown that damping coefficient for various modes of blast loading with different duration, will be different [14]. In accordance with the recommendations of reference [20], damping coefficient for concrete structures under blast is a maximum of 1%. The reason for this has been expressed the slight damping effect on the first maximum response of structure under blast, which usually is the only important response. On the other hand, absorption strain energy during plastic deformation is much more than the energy that is absorbed by the structural damping. Usually damping effects on the first maximum response of structural member under blast loading is small but the support reactions and maximum stresses in the structures are affected by damping [15]. On the other hand, ignorance of damping is in line with increase the safety factor of calculations [2,20,33-35]. According to this description, in the created SDOF models in this article, the system damping has been ignored. Thus, the overall dynamic equation of motion for SDOF model without damping is expressed as Equation 4 [32].
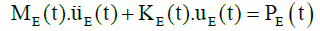 (4)
(4)
Where PE(t) is the equivalent external load, ME(t) is equivalent mass, KE(t) is equivalent stiffness and uE(t) is the equivalent displacement for SDOF system and refers to the acceleration of the system. For a column with simple ends (hinges) under uniform lateral load, SDOF model can be described as shown in Figure 3-a. The SDOF system behavior has been assumed elastic-plastic and can be displayed with a bilinear load-displacement diagram as shown in Figure 3b.
In the figure above, N is constant axial load, KEpl is plastic stiffness, KEel is elastic stiffness, uEu is the ultimate displacement, uEy is the yield displacement, Pu is the ultimate load and Py is the yield load. Next, how to calculate the equivalent SDOF system resistance function parameters for the reinforced concrete beam-column with hinged supports has been explained. P-δ effects will be entered explicitly in the calculations of SDOF model of column under uniform distributed blast load. The process in this case is that in each time step of calculation, dynamic uniform equivalent lateral load (ELL) is applied to the column so that the maximum moment resulted from this load is equal to as the maximum bending moment caused by axial load with the same eccentricity equal to calculated displacement at that step. η(t) the equivalent lateral load correspond to the effects P-δ for a one-way member with hinged supports is calculated by Equation 5 [12,36]. This load must be multiplied by equivalent load factor kL for SDOF model.
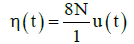 (5)
(5)
In a simple beam under uniformly distributed load using equilibrium equations can determine the yield and ultimate load (Pu, Py) in terms of lateral load of blast:
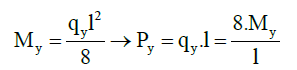 (6)
(6)
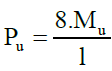 (7)
(7)
In the above Equation 5-7, qy is the effective uniform lateral load on the column (blast load plus equivalent lateral load of P-δ effects) at the yield state and qu is the uniform distributed load at the ultimate state. Also, My and Mu values are determined according to momentcurvature diagram for the section. If θu and θy are section curvature values in the ultimate and yield state respectively, using the theory of elasticity the yield displacement uEy in the middle of length of the beam can be approximated as follows:
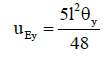 (8)
(8)
Where the kE,el elastic stiffness of SDOF system also can be calculated by Equation 8 and 9.
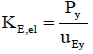 (9)
(9)
To calculate the displacement in the ultimate state uEu, the assumption is that a plastic hinge had been composed in the middle of the height in which the lp is the length of plastic hinge. Here ψp is the plastic rotation after the formation of the plastic hinge and uEy represents displacement value in the middle section. Plastic displacement in the ultimate state uEpn, can be calculated from Equation 10 (with small displacement assumption).
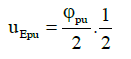 (10)
(10)
Where, ψpu is the plastic rotation in the ultimate state. If in this case, the plastic curvature θp is constant through the length of plastic hinge 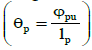 ultimate displacement can be calculated by Equation 11.
ultimate displacement can be calculated by Equation 11.
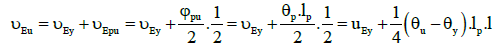 (11)
(11)
Finally, the plastic stiffness of SDOF system can be achieved by Equation 12.
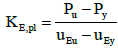 (12)
(12)
In order to estimate the plastic hinge length, several equation 13 have been proposed [37,38]. For example, the suggested equation by Pauli and Priestley can be noted [39]:
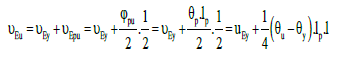 (13)
(13)
Where, db is the longitudinal bar diameter. According to the moment-curvature (M-θ) diagram of section and fitting of a bilinear function to it (in the elastic and plastic parts) the yield and ultimate points My` Mu` θy and θu are determined (Figure 4). Thus, the necessary load-displacement diagram (resistance function) for describing the SDOF model Py` Pu` θy and θu are determined.
In blast case with medium to long distance from the structure face, pressure distribution on the structural face can be assumed to be uniform [1,2,28,34-40]. In practical applications and with design purposes the time history of blast pressure in the positive phase can be idealized linearly as shown in Figure 5 [1,2,41]. The amount of pressure at the time of reaching the blast wave to the structure is equal to reflected pressure pr0 which with a conservative estimation, blast load can be assumed triangular with maximum pressure pr0 and duration time td or clearing effects can also be taken into account [3]. In this case, a history of triangular loading which its beneath area is equal to the area of dashed line loading graph in Figure 5, will be considered. The clearing effects is a phenomenon that occurs due to the limited dimensions of structure surface subjected to blast loading and reduces the duration of blast pressure in compared with the case in which dimensions of surface is unlimited [2,33,41].
Duration of equivalent triangular load (te) is calculated by following Equation 14.
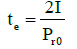 (14)
(14)
Where, I is area under the bilinear curve in Figure 5 and is obtained from Equation 15.
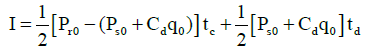 (15)
(15)
The description of the blast parameters including incident over pressure Ps0, dynamic pressure q0, tc cleaning time and td blast duration time of the positive phase of blast (without cleaning effects) and how to estimate them according to the amount of explosive material and the distance between the center of the explosion to the structure, can be found in the various references of structural blast loading [1,2,33]. It should be noted that the pressure resulted by blast is multiplied to column width and is applied as uniform distributed throughout the column's external surface. This blast loading method is consistent with design references, such as [1,2] and other studies [7,13,34].
Using ideal triangular blast load with duration time td three different loading regimes can be defined [21,33], impulsive loading regime, dynamic regime and quasi-static regime. In the impulsive regime, tmax (when the maximum displacement occurs) is much longer than td. In dynamic regime these two times approximately are near each other and in the quasi-static regime tmax is much shorter than td. Note that in the quasi-static regime, if the rise time of pressure is so long that the structure does not create inertia forces, loading will be turned to complete static load [2,23].
Moment-curvature Analysis of RC Section
The finite element software OpenSees, which has been created by the PEER center, can simulate the behavior of various structural systems [37-42]. This software is an open code and free package that using finite element method, analyzes a variety of structures and has modules that simplify the modeling and analysis process. To perform RC section analysis in OpenSees, three different material model for steel, non-confined concrete and confined-concrete (core of the section) should be defined. Here, In order to M-θ analysis a subprogram that exists in finite element software OpenSEES has been used [43]. In this subprogram, the classical theory of Euler-Bernoulli to calculate moment-curvature of reinforced concrete section is used [36]. The concrete materials model Concrete01 Material-Zero Tensile Strength type has been selected [44] which is based on the model of Kent-Park regardless of the tensile strength of concrete [45]. In this model, the stress in the confined core concrete is calculated using the following Equation 16:
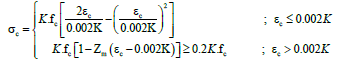 (16)
(16)
Where, fc is the compressive strength of standard cylindrical sample of concrete (MPa), εc is strain in the concrete. Parameters in this equation 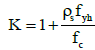 and
and 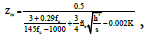 in which
in which 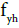 is stirrup yield stress, ρs is stirrup volume ratio to the core volume of the concrete, h is the width of concrete core in mm (from outside of stirrup) and s is stirrup intervals (mm). Maximum concrete stress is equal to
is stirrup yield stress, ρs is stirrup volume ratio to the core volume of the concrete, h is the width of concrete core in mm (from outside of stirrup) and s is stirrup intervals (mm). Maximum concrete stress is equal to 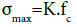 which occurs at the strain
which occurs at the strain 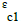 =0.002K and the ultimate stress is also assumed to be
=0.002K and the ultimate stress is also assumed to be 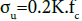 that at the ultimate strain
that at the ultimate strain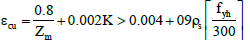 will occur.
will occur.
For covering concrete (non-confined) in the above equations 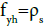 =0 assumption is made.
=0 assumption is made.
For steel rebar material model, linear elastic-perfect plastic has been used which is available in OpenSEES library as Steel01 Material model. In Figure 6 an example of obtained moment- curvature diagram for assumed column section at the initial state (without strain rate effect) with different levels of axial load has been shown. Characteristics of the section are described at section 6.
The equation of motion of single degree of freedom system without damping, under dynamic load PE is described with an ordinary differential Equation 17 as follow, where u(t) is displacement of the middle height of column.
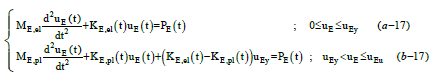
Elastic and plastic stiffness (KE,el and KE,pl) are dependent on time and slightly modified in each computational step, due to the effects of strain rates.
The equivalent load PE is expressed with a simple equation PE=KL Both sides of the equation 17 can be divided to the load coefficient of and thus all available statements, other than statements of equivalent mass, will be equal to its actual value and elastic and plastic equivalent mass (ME,el and ME,pl) will be obtained by multiplying the total mass of the column (Mb) to load-mass coefficient (KLM) which for a simple member with a distributed uniform load we have: ME,el=0.78Mb and ME,pl=0.66 Mb.
So, we have:
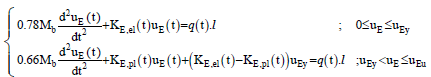 (18)
(18)
At the next section, solving this differential Equation 18 by finite difference method FDM will be done [44-46].
According to available experimental results, with increasing strain rate, tensile and compressive strength of concrete remarkably will be increased [47-50], its elasticity modulus somewhat will be larger [47,51], the propagation process of cracks [47,52] is changed and ultimate strain of concrete also is increased [53,54]. At high strain rates, steel material's strength often up to 50%, compressive strength of concrete to 100% and tensile strength of concrete up to 600% increase [55]. Dynamic increase factor (DIF) describes the ratio of dynamic resistance of material to its static resistance and is applied for considering the increasing strength of materials at high strain rates [48,55]. According to the recommendations Comité Euro-Internationaldu Béton (CEB), DIF factor for concrete in compression is in accordance with Equation 19 [56]. This equation for strain rate range of 30×10-6 to 300 S-1 is valid.
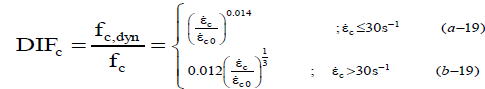 (19)
(19)
In which the subtitles dyn represents the dynamic state and  Dynamic increase coefficient for strains corresponding to the maximum and ultimate stress of concrete respectively has been given with Equations 20 and 21 [56].
Dynamic increase coefficient for strains corresponding to the maximum and ultimate stress of concrete respectively has been given with Equations 20 and 21 [56].
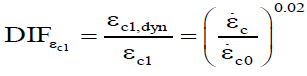 (20)
(20)
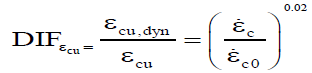 (21)
(21)
In reinforcing steel at high strain rates, yield and ultimate stress is increased and its ultimate strain is also increase [47,55,57]. Malvar and Crawford from published data resulted by high strain rate tests on steel bars, have suggested an Equation 22 to estimate steel DIF coefficient for ultimate and yield stress as follows [55].
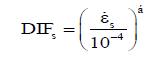 (22)
(22)
In which for the yield state α=0.074-0.040×fy/414 and for the ultimate state is α=0.019-0.009×fu/414 that fy and fu are static yield and ultimate strength of steel, respectively. The above equation is established for steel with yield strength of 710-290 MPa and strain rate of 0/0001 to 225 S-1. Basically, in the various strain rates no change is considered in the elastic modulus and the strain of reinforcing steel [47,56-58].
Finite difference form of SDOF system's motion of equation (Equation 18) in the elastic and plastic range is expressed as below Equation 23:
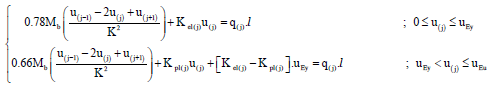 (23)
(23)
Where K represents duration of time steps and subtitle j is the number of calculations step. Here, using MATLAB- R2013a (v8.01) software the main body of the program has been written to solve the above equation and the subprogram for preparation of M-θ diagram using OpenSees software has been prepared. In this article, time step has been selected equal to 10-5 seconds and at every step considering initial and boundary conditions, the following steps are performed respectively:
M-θ diagram is plotted with OpenSees subprogram and bilinear resistant function is extracted from it.
By solving differential equation of motion under lateral uniform distributed load, the equivalent transverse displacement uE is determined and then equivalent speed ÅE =duE/dt is also calculated considering changing the amount of displacement relative to the previous step.
The equivalent curvature θE and curvature rate θE =dθE/dt using Equations 24 and 25 is determined:
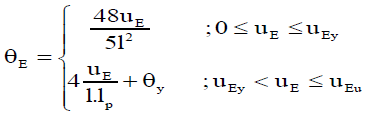 (24)
(24)
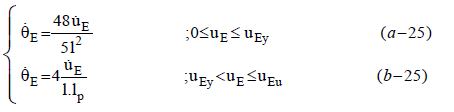 (25)
(25)
Using the value of θE the bending moment Mθ from the curve of bilinear moment-curvature is determined and then the location of neutral axis  of the section can be calculated using integral Equation 26. This equation has been obtained by writing the Equation 26 of rotational equilibrium around s steel under the moment of Mθ (refer to Figure 2).
of the section can be calculated using integral Equation 26. This equation has been obtained by writing the Equation 26 of rotational equilibrium around s steel under the moment of Mθ (refer to Figure 2).
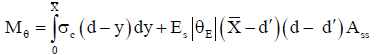 (26)
(26)
With replacing concrete behavior equation in accordance with the Equation 16 in the above equation and according to Euler-Bernoulli theoretical assumptions, we have:
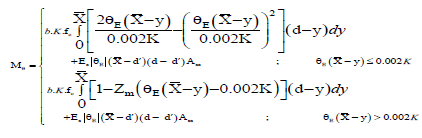 (27)
(27)
In the above Equation 27 the only unknown is X and yielding of steel Ass should be controlled; i.e., if 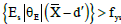 rather than it the amount of fys is replaced and the equation will be solved again.
rather than it the amount of fys is replaced and the equation will be solved again.
Strain rate amounts in concrete and reinforcing steels are calculated using linear strain distribution assumption in the section with Equation 28 [59].
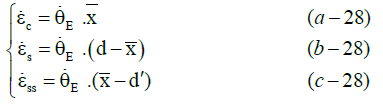 (28)
(28)
Considering the resulting strain rate values (step 5), DIF factors for compressive strength of concrete, concrete strain in the maximum compressive stress, ultimate strain of concrete, yield stress of steel and finally, ultimate steel stress are determined using the corresponding equations and for begin the next step, M-θ subprogram is called using these new characteristics of materials and the new resistance function of section will be determined.
Initial and boundary conditions for a two ends hinged beam-column are that the displacement and curvature at the beginning and end of the beam-column, at any time, is zero and velocity and displacement at all points in zero time (start of analysis) is equal to zero. By applying initial and boundary conditions, at each step j we can determined u(t) and as well initial conditions for the next step, namely j=j + 1, is also determined. The completion criterion of this cycle, namely the criteria of failure, is reaching the compressive strain of concrete to the ultimate strain.
As previously described, for considering the effects of secondary moments due to the axial load on the column, at every step of FDM calculations, the value of η(t)=8N.u(t)/l2 is added to existent lateral load q(t) that N is the existent compressive axial load and u(t) is the equivalent amount of displacement from the last step of calculations. In fact, by adding load η(t) to existent lateral load , the concept of reduced resistance function has been used [36].
Comparison between Results of SDOF Model with the Finite Element Model
Here, reinforced concrete columns model with the shown properties in Figure 7 and Table 1 is considered. The considered column has a rectangular section with symmetric reinforcing and the applied concrete with characteristic strength of 30 MPa and member span length of 3 meters is assumed. This column is under effect of constant axial load of 600 kN and lateral blast load of 40 kg TNT at a distance of 4 meters from the side of the column (in the middle of its height). Time History of blast pressure on the face subjected to blast is set with described method in section 3 and it is assumed that the spatial distribution of this pressure on the column surface is uniformly distributed.
The presented SDOF analytical process has been used to study dynamic behavior of reinforced concrete beam-column model. Further details and quantities of basic assumptions for them at the beginning of the calculations is listed in the following Table 1.
| Parameter | Initial Value |
|---|---|
| 0.0035 | ultimate strain of concrete in compression áµï¿½cu |
| 0.00235 | strain of concrete corresponding to maximum compressive stress áµï¿½c1 |
| 30 Mpa | characteristic compressive strength of concrete fc |
| 400 Mpa | Steel yield stress fys |
| 600 Mpa | ultimate stress of steel fus |
| 200 X 103Mpa | Modulus of elasticity for steel Es |
| 10-5Sec | Time step duration for finite difference calculations K |
Table 1: Characteristics of the considered beam-column at the beginning of the calculations.
In order to verification the obtained results from the analysis of above column with SDOF method introduced here, a two-dimensional finite element analysis to analyze the dynamic response of column under blast loading using OPENSSE software, has been done. Models of selected materials have been the same with described models in M-θ subprogram and here the version of V(2.3.1) of this software has been used.
Because of the symmetry of geometry and loading, the model has been made two-dimensional and longitudinal elements of disp Beam Column type with 10 points of integration with dimensions of 10 cm in length have been selected. For longitudinal reinforcement Straight type element has been used. To define the column section, the fiber model has been used that divides the section to concrete fibers (with dimensions of 3 cm) and steel bars. Because the two-dimensional model in OpenSEES is analyzed quickly, here no specific study has been done to determine the optimum size for the elements. In the two ends of column the ideal hinged and roller support bearings are defined.
In the rules and algorithms of OpenSees no prediction and recommendation exist on how to import the effects of strain rate. So, here strain rate effect on dynamic characteristics of materials is considered using DIF coefficients of the last step of the calculation of SDOF model. Analysis of the considered column with OpenSEES, consists of three distinct phases; First, the column is taken under a static analysis (without considering DIF factors) to its axial load before the blast. During this phase, the displacement of nodes in the roller support along the longitudinal axis of the column is recorded (phase I). Then, dynamic model with applying DIF coefficients to the material models is done and during another static analysis, the determined displacements from the first phase is applied to the end nodes (phase II) and then dynamic analysis under lateral loading of blast takes place (phase III). Thus, for dynamic analysis under blast loading, the column model can be updated for considering the effects of strain rate.
In Figure 8, the amount of calculated first maximum lateral displacement for the column in SDOF model has been compared with the results of finite element analysis. Note that the result of finite element analysis has been recorded from applying of blast load to the structure. It can be seen that the way of the displacement increasing with time is very close to the results of finite element analysis but reaching to the criterion of section failure has caused the maximum displacement to be less than the amount calculated in software OpenSees.
P-I diagram
In the elastic SDOF model equation, external work performed by external loads of quasi-static is defined by the Equation 29
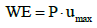 (29)
(29)
Where P is external force and umax is the maximum displacement. Strain energy for SDOF system is calculated by Equation 30 as follows (k is the stiffness of system).
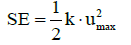 (30)
(30)
Which by putting SE and WE, we have:
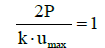 (31)
(31)
The Equation 31 represents the quasi-static asymptote line in the dimensionless P-I diagram (Figure 1). If an impulse load is entered to the model, the initial speed can be calculated with the following Equation 32 where I is blast resulted impulse and M is the equivalent mass of SDOF system.
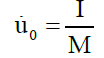 (32)
(32)
Now, the transferred kinetic energy to the structure can be expressed as Equation 33 that finally by putting SE and KE equation, the Equation 34 is resulted.
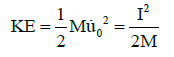 (33)
(33)
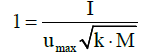 (34)
(34)
Considering a specific damage level, the points on the curve P-I represents the combination of pressure and impulse combination that can cause that level of damage. For a RC column (or beam-column), the level of damage (damage criterion) can be maximum bending deformation in the middle of the length [4,22,26,27,59,60], maximum shear deformation in the supports in case of shear failure [61,62], maximum rotation in the supports and connections [4] or residual axial capacity of beam column [28].
However, usually the maximum structural deformation is considered as failure criterion. Here, using introduced SDOF model drawing a diagram of P-I reinforced concrete column has been addressed so that flexural deformation at mid-span (maximum transverse displacement) has been considered as a measure of failure. Failure criterion has been assumed equal to deformation corresponding to 2 degrees rotation of supports that usually crushing of compressive concrete is occurs on this amount of support rotation [2].
Here, the effect of the axial load has been discussed on the diagram P-I of reinforced concrete column. The obtained P-I curves derived from model SDOF, under lateral load of blast with triangular time history has been shown in Figure 9. It can be seen that the amount of axial load is more effective on the position and form of the P-I diagram. In this figure, parameter N is the column maximum pure axial strength without considering blast effects. It can be seen that with increasing axial load, horizontal and vertical asymptote and the curve reduce and gets closer to the coordinates center. This implies the reduction of column resistance against the blast loading at the impulsive and quasistatic regimes.
The increase in axial load level, lead to increase in flexural capacity of beam-column section, but decreases the maximum rotation of support (at the failure state), which subsequently the absorbed strain energy is also reduced. Therefore, maximum resisting blast load by beam-column is reduced compared with the case of without axial load.
In this paper, a single degrees of freedom (SDOF) approach based on Euler-Bernoulli theory is introduced in order to estimate dynamic response of reinforced concrete column under lateral load of blast. In the SDOF model the effects of secondary moment (P-δ), nonlinear material behavior and effects of strain rate has been considered. Through the calculations steps, the resistance function of column considering those effects is updated. Blast load has been assumed as a uniformly distributed pressure on the column face which has triangular time history. Of course, the presented SDOF model can be used with any desired time distribution for lateral load of blast. Then, the introduced SDOF model is used for drawing P-I diagrams of reinforced concrete column considering its constant axial load. According to the results, presented SDOF method despite the simplicity and low time for the calculation has sufficient accuracy and reliable results. It has been shown that P-I diagram is affected by the amount of axial load. So that, by increasing axial load this diagram is closer to the co-ordinates center indicating reducing the amount of necessary pressure and impulse to achieve the target level of damage. This matter shows the importance of considering axial load for assessment or design of RC columns under blast loading. In SDOF approach, with using equivalent coefficients or equivalent length of plastic hinge, some approximations take into account, and also useful information such as displacement, curvature and rotation profile can't be achieved through the column. On the other hand, uncertainty in the nature of the blast load causes that the accuracy of the idealized system can't be guaranteed. However, in this method a good understanding of the parameters affecting the structural behavior and its dynamic response can be achieved. SDOF results should be conservative because this method is useful for design purposes. Thus, it is useful to study overall response of RC columns with SDOF techniques and local responses of structure, such as blocking, spalling and pitting, can be analyzed with explicit finite element method.
In order to continue this study, the reduced section method will be used to change the criterion of calculations completion. In the calculation steps of SDOF equation of motion, whenever concrete compressive strain reaches to its ultimate value, the crashed concrete will be removed from the section and equilibrium equations will be written for the new section. In addition, negative phase of blast will be taking into account to study its effects on the accuracy of calculated displacement.