International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2016) Volume 7, Issue 4
The numerical simulation was performed to analyze the film thickness on horizontal circular tube in a falling film evaporator. A complete description of the falling film thickness is obtained. The shape and thickness of the falling film with variation of Reynolds numbers along with tube spacing is computed and compared favorably with the published experimental findings. The volume of fluid (VOF) method is implemented to track the motion of liquid falling film and gas liquid interface in the commercial CFD package where the primary phase is represented by air and the secondary phase by the liquid, Fluent is used for this numerical study.
<Keywords: Numerical simulation; Ansys fluent; CFD; VOF; Horizontal circular tube; Tube spacing
Evaporation of thin liquid falling films from horizontal circular tubes is of fundamental interest and widely used in refrigeration equipment, chemical and food industry such as heat pipes and capillary pumped loops, spray and jet impingement cooling, falling film evaporation and so on [1–4] as it provides high heat transfer rate and small use of liquid. For a fully developed laminar film flow, heat transfer across the film is approximately evaluated by one dimensional heat conduction. The circumferential thickness of a falling liquid film is inversely proportional to the local heat transfer coefficient. Hence, the local film thickness is an important property to characterize the falling film and heat transfer phenomena. This in turn indicates that deeper insight into the film thickness distributions is of critical importance for many applications.
Since the characteristics of falling films have drawn great attention, the researches on the film thickness have been conducted by both theoretical and experimental approaches in the past years. Nusselt [5-7] first analyzed falling films theoretically, assuming a continuous sheet flow from tube to tube and momentum effects on the falling films to be negligible and derived the following expression for the film thickness:
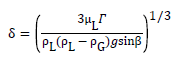
Where β is the circumferential angle measured from the top of a horizontal tube and Γ is the liquid flow rate on one side of the tube. With this definition, the film Reynolds number is given below
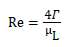
Zhang et al. [8-14] presented theoretical and experimental investigations of the film thickness and temperature profile on a vertical heated/cooled plate. Xu et al. [15] studied the flowing state in liquid films outside horizontal tubes. Numerical methods based on the Computed Fluid Dynamic were also applied to explore the construction and instability of the film [16,17].
Adams et al. [8] reported falling film for heat exchangers and suggested three advantages of the falling film: the pressure drop of the falling film is negligible, the quantity of liquid required is small, and the heat transfer coefficients are high. Kocamustafaogullari et al. [9] have simulated the hydrodynamics and heat transfer of the liquid falling film on a tube to obtain the film thickness and local average heat transfer coefficients for both constant heat flux and isothermal boundary conditions. Rogers et al. [10] solved the motion and energy equations for the laminar liquid film flow by considering following: film thickness as a function of Reynolds number, Archimedes number and the angular position. Mitrovic [11] studied experimentally that the heat transfer and the mechanism of the fluid flow from a horizontal heated tube to a sub cooled liquid falling film. The experimental results indicated that the flow pattern of the falling liquid depends on both Reynolds number and the tube spacing [12].
However, despite above numerous theoretical and experimental studies, there has been little information available for film flow characteristics on horizontal tubes. In this paper, we present a detail numerical simulation of the flow field, which could not be observed experimentally, on horizontal circular tubes with different tube spacing and Reynolds numbers. First, the experimental data was numerically simulated and validated with the help of Ansys fluent using volume of fluid model. Then, the thickness of liquid film on tube were investigated. Furthermore, the effect of tube spacing and Reynolds numbers on film thickness was considered. Finally, numerical results were compared to theoretical values by Nusselt expression and the reported values.
Analysis geometry and physical condition
Ansys fluent has been employed to model and mesh the domain of the geometry. A tri pave mesh has been generated for the 2D domain. The region around the cylinder wall was carefully meshed by using a boundary layer technique to capture details of the liquid flow around the cylinder and the tracking of a liquid-gas interface for 2D flow field simulations which is shown in Figure 1a and Figure 1b respectively. The domain consists of three phases, where gas represents the surrounding air, liquid represents water and the solid phase is the wall for the cylinders. A size function technique has been employed which enables starting from a minimal mesh size where flow details are important. It was assumed here that the falling film flow over the horizontal tube is incompressible, low-velocity and viscous flow derived by gravity down ward as shown in Figure 2.
The properties of the surrounding gas phase, air, and the liquid phase, water, were considered constant under the normal condition with temperature of 25°C and pressure of 101.325 kPa. Considering its symmetrical structure, the shaded region was chosen as the solution domain to minimize the computing time. The solution domain was discretized by quadrilateral elements, as shown in Figure 1b. The total number of mesh elements and the time step were kept 70,147 and 0.1 ms respectively. The grid size increases with distance from the cylinder surface, as flow gradients become sever. The size function was chosen here 0.003 m with growth rate of 1.1 to a size limit of 1 (Table 1).
Figure 1: The 2D flow field model (a) Boundary conditions of the domain with three phases, including the three solid horizontal cylinders (b) Tracking the interface in 2D of the liquid (red) over the three horizontal cylinders and the surrounding air (blue). The scale on the left denotes 1 for water and 0 for air.
| S No. | Settings | Choice |
|---|---|---|
| 1 | Simulation | 2D |
| 2 | Solver | Segregated implicit |
| 3 | Model | VOF |
| 4 | Material | Air – primary and water – secondary |
| 5 | Gravitational acceleration | 9.81 |
| 6 | Volume fraction | 1 for water and 0 for air |
| 7 | Pressure Velocity Coupling | PISO |
| 8 | Discretization Pressure | PRESTO |
| 9 | Discretization Momentum | 1 Order Upwind |
| 10 | Top boundary | Velocity inlet and pressure inlet |
| 11 | Left side boundary | Pressure outlet |
| 12 | Right side boundaries | Symmetry |
| 13 | Bottom side boundary | Pressure outlet |
| 14 | Wall boundary | Cylinder’s edge |
Table 1: Fluent 2D simulation settings.
Governing equations
To track the interface between two phases, volume of fluid (VOF) model is used to compute two separate phase flow [18] whereas Fluent solves conservation equations for mass and momentum and volume fraction function [17].
Mass equation
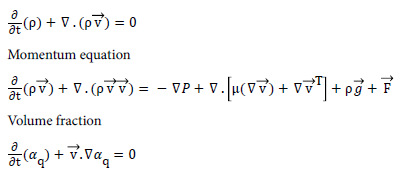
Verification of computational method
The comparison of the calculated results from Nusselt correlation [19], the experimental results by Gstoehl et al. [20] and simulated results of this paper are plotted against the circumferential angles and film thickness shown in Figure 3a and b. It is seen that the relative error between the simulation results of this paper and the calculated results from Nusselt correlation is within the range of 20% approximately and the variation trend of the simulation results of this paper well agrees with the experimental data by Gstoehl et al. [20]. It should be noticed that the thickness of falling liquid film between 0 and 40 by Gstoehl et al. [20] does not vary monotonously. This is caused due the measurement error and should not be considered as a normal phenomenon. The comparison results shows that the VOF method is capable of capturing the characteristics of falling film thickness on horizontal tube under adiabatic condition. Therefore, this method is recommended for predicting the film thickness characteristics over horizontal tube.
The effect of Reynolds number (Re) and tube spacing(s)
When the surface of tube is fully covered by the liquid film, the following heat and mass transfer during the process is considered as steady state with constant boundary conditions. The effect of Reynolds number on the distribution of film thickness in the circumferential direction of a horizontal circular tube with tube spacing (s), 19.4 mm is shown in Figure 3b and the circumferential distributions of falling film thickness for all three different Reynolds numbers are similar to each other. It means with the increment of circumferential angle, the film thickness decreases first and then increases after the minimum value of film thickness which appears in the circumferential range between 100o to 140o. However, the Reynolds number affects the amount of the film thickness and this result is consistent with the experimental result by Hou et al. [21], who has verified the effect laws of Reynolds number on film thickness by using displacement micrometre.
The tube surface which is covered by liquid film has two typical positions in the circumferential direction one is the upper stagnation point, 0° and second is the lower stagnation point, 180° where the circumferential velocity of liquid film equals to zero. The stagnation film thickness increases as Reynolds number increases. Apparently the centrifugal force induced due the circular motion of liquid film that is directly related to the liquid film velocity which has overcome the adhesive force between the tube surface and the liquid film. The most of the liquid is thrown off the tube surface even the lower stagnation point is not reached. Compared to this part of liquid, the liquid film which stays on the tube surface has very low velocity. The corresponding centrifugal force is not big enough to overcome the adhesive force. Therefore, it continues to flow along the tube surface till the lower stagnation point is reached that means the liquid stays longer over the tube surface when the Reynolds number is small. The similar phenomenon near the lower stagnation point was also observed by Min and Choi [22] when the Reynolds number is greater than 40. The film thickness on the top of the tube tends to decrease with increased tube spacing, which is logical because of the added momentum of the falling liquid by Gstoehl et al. [20].
The falling liquid film is in steady state after it fully covers the surface of tube under the constant boundary conditions. The circumferential distribution of falling film thickness over the tube surface is not uniform which decreases from the top of the horizontal tube and then increases after it reaches to the minimum value of approximately which appears within the circumferential angle range between 90° to 140°. The asymmetric distribution, contradictory to the Nusslet theory is supported by the results of various experimental researches. The circumferential distribution of falling film thickness along the tube surface corresponds to the variation of liquid film velocity which indicates that the momentum effect on the flow cannot be neglected.
The falling film thickness increases with the increase in Reynolds number which is directly related to the mass flow rate of liquid. The sizable zone that is lack of liquid is formed near the lower stagnation point and the zone size is bigger for higher Reynolds number.
The film thickness on the top of the tube tends to decrease with increased tube spacing, which is logical because of the added momentum of the falling liquid.