Journal of Biomedical Engineering and Medical Devices
Open Access

Methodology of Evaluating Pulling Performance of Laparoscopic Electrode Hook

Yuan Kang, Xiaoxin Wang, Lijun Zhu and Peng Zha^{* *}Correspondence: Peng Zha, Research, Technology & Clinical Department, Medtronic China R&D, Shanghai, P.R. China, Tel: + 862133230241, Email:

Author info »

Introduction

Electrosurgery refers to the application of high-frequency (radio frequency) current to cutting and coagulation of tissues. Electrosurgical devices are frequently used during surgical operations to help limit blood loss due to their ability to make precise cuts [1,2]. However, the thermal spread of using electrosurgical devices is gaining more attention nowadays because the high thermal spread will increase the risk of thermal injury to tissue and organs [3,4]. Since the thermal spread has been reported to be highly related to the power setting and activation time [5,6], this study is aimed to explore the dissection capability with minimized power settings to get a favorable thermal damage outcome.

Laparoscopic surgeries are widely adopted with many benefits such as short hospital stay, fast recovery time, and low complication rate compared to open abdominal procedures [7]. Electrode hook is one of the common devices used in laparoscopic surgeries [8]. Generally, in laparoscopic surgery, the inside part of the electrode is used to dissect the tissue. To ensure the effectiveness of dissection, surgeons will increase the power during the operation. As a result, the thermal damage caused by excessive power will be harmful. Achieving a good anatomical effect and enhancing cut efficiency at the set power is a major problem in electrode design. As the main indicator for the performance and efficiency of electrodes during dissection is the pulling force, measuring it at a set power during the dissection is a critical question.

In this study, we compared the cutting efficiency and thermal damage between a novel design by adding an edge on the inner side of the electrode hook and the commercial device CleanCoat™ (Table 1). We proposed that this addition of an edge would make the cutting edge sharper and therefore can reduce the pulling force. Moreover, reducing the contact surface area would increase the radiofrequency (RF) current density via geometry, thereby reducing the power and force required to transect tissue.

Table 1: Pictures of the novel design and CleanCoat™ device.

As electric field and thermal spread in biological tissue are difficult to measure and predict, modeling is a necessary tool to understand electric and temperature distribution [9]. In this study, we established a finite element model (FEM) of the monopolar electrode to simulate the cutting efficiency and assess the thermal damage in biological tissue during the electrode cutting process. FEM model can provide detailed insight into the electric field in the electrode cutting direction and tissue heat transfer. More specifically, a coupled thermal-electric FEM model was applied with temperature-dependent electrical and thermal properties for the tissue and distance-related electrical and thermal contact property between tissue and the electrode.

Application of high frequency (monopolar) energy in vivo is a highly variable process, with the surgical technique weighing heavily on the resulting tissue effect and drag or pulling force. The speed and depth at which the electrode moves through the tissue greatly determine the outcome. Ex vivo tissue has the advantage of providing a controlled environment for energy application. The controlled motion including the depth, angle, and speed of cut enables a decrease in experimental uncertainties and thus reduces measurement variability beyond what can be achieved by testing in in vivo tissue.

This study was designed with a combination of an ex vivo bench test that allowed us to assess the pulling force and an in vivo porcine model to explore the lowest power for cut by considering the real use condition (Figure 1).

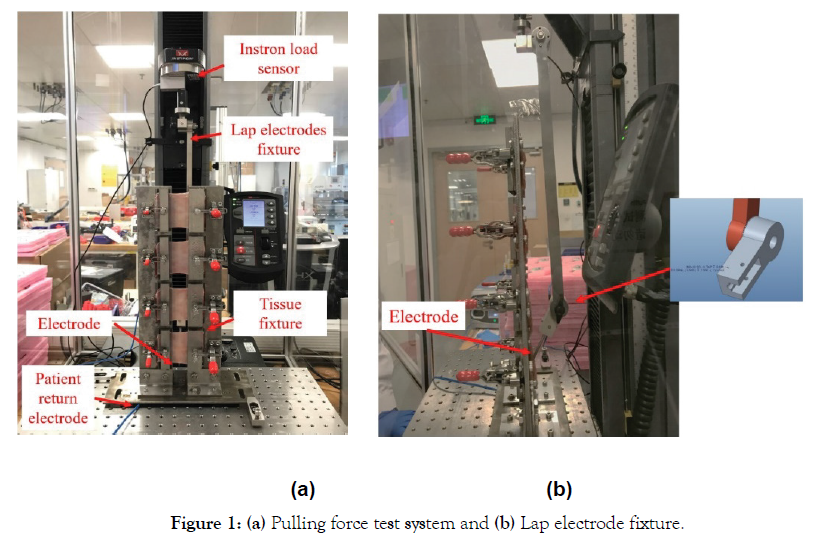
Figure 1: (a) Pulling force test system and (b) Lap electrode fixture.

Materials and Methods

Electrode design

Table 1 shows the appearance of the two different electrodes. The traditional L-Hook electrode design is a cylindrical cutter head and the cross-section of the cutter head is round (Figure 2a). The novel electrode was aimed to reduce the contact area between the electrode and the tissue during the operation through remodeling the cutter head, as shown in Figure 2a. It was proposed that the novel design would increase the energy charge concentration, and discharge through the tip to improve the cutting effect.

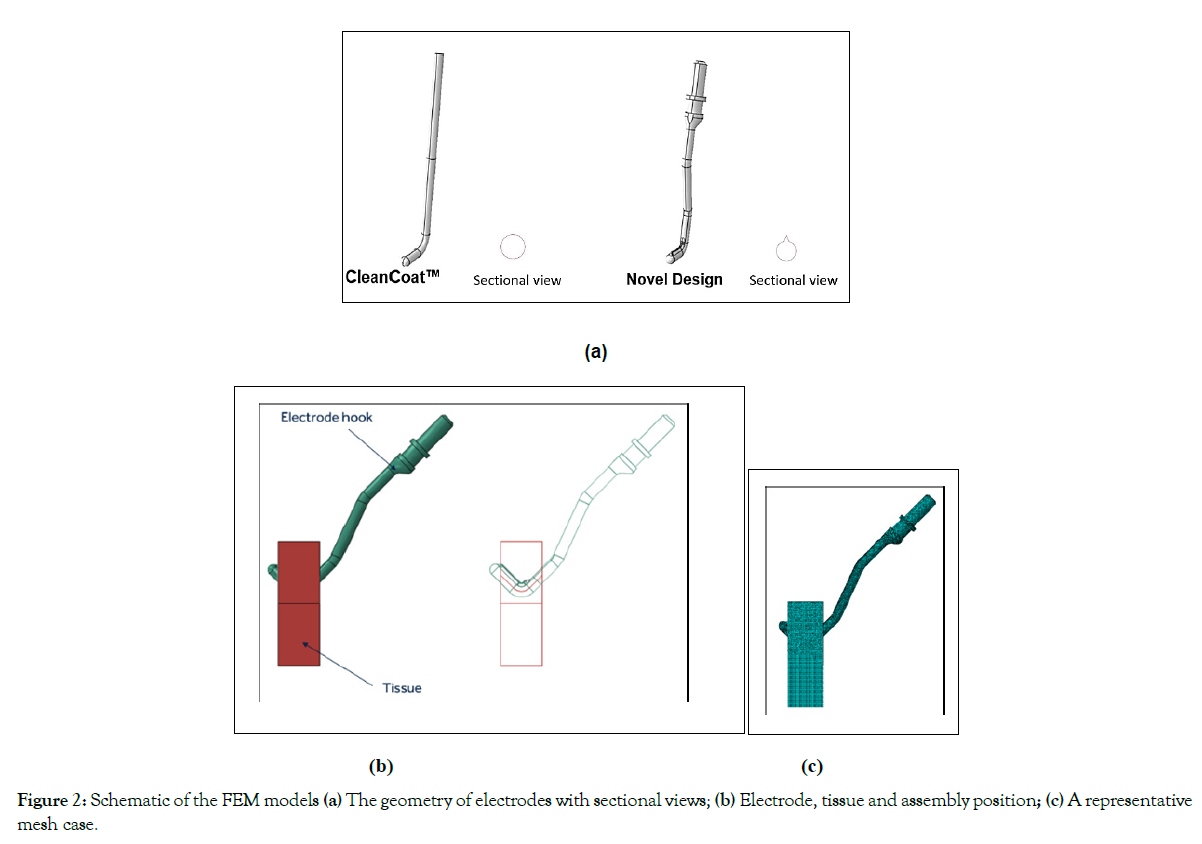
Figure 2: Schematic of the FEM models (a) The geometry of electrodes with sectional views; (b) Electrode, tissue and assembly position; (c) A representative mesh case.

Pulling force testing method and equipment

The study was tested on an Instron pulling force test system. The system consists of Instron equipment (Load Cell 2530-100), a lap electrode fixture, a tissue fixture, an FT10 Energy platform, a footswitch, and a patient return electrode (Figure 1a).

This evaluation was performed on a day-old ex vivo tissue. Porcine stomach with 3.7-4.2 mm thickness was cleaned with saline and cut in the same size and fixed in a tissue fixture. The electrode hooks (E3773-CleanCoat™ Laparoscopic Wire L-Hook Electrode, E3774 CleanCoat™ Laparoscopic Flat L-Hook Electrode, and novel design wire and flat L-hook) were fixed in the laparoscopic electrode fixture (lap electrode fixture) with a certain dissection angle. The fixture was connected to Instron and the electrode generator (Valleylab™ FT10 Energy Platform, Covidien) (Figure 1b), and the patient return electrode was connected to the bottom of the tissue fixture. Experimental setting parameters, including speed, mode, power, and angle of dissection were selected; the footswitch was used to control energy excitation when the electrode was dissecting tissue. The maximum load was recorded automatically by the Instron software system and pulling force was measured automatically while the electrode was dissecting the tissue.

Simulation analysis evaluation

Fem formulation: The analytical modeling of heat transfer in tissue, or bioheat transfer, to account for heat sources and sinks from metabolism and blood perfusion was the pioneering work of Pennes [10]. The bioheat transfer model of tissue includes coupled thermal and fluid (blood) transport phenomenon. Previous work has shown that solid elements can be used to model tissue, a multiphase material consisting of both solid and liquid, with sufficient accuracy [11]. The linear bioheat transfer equation for temperaturetissue is the general heat equation for conduction with added terms for heat sources and sinks and can be expressed as [10]:

(1)

where ρ, c, and k are tissue density (kg/m³), heat capacity (J/kg·K), and thermal conductivity (W/m·K), respectively, ω_b is the effective blood perfusion parameter (1/s), ρ_b is the blood density (kg/m³), C_b is the blood heat capacity (J/kg·K), T is the local tissue temperature (°C), T_b is the blood inlet temperature (°C), q_m is the metabolic heat generation rate of the tissue (W/m³), q_q is the externally induced heat generation rate due to electrosurgical heating of the tissue (W/m³), and t is time (s). For all cases, it was assumed that the metabolic heat source and blood perfusion were zero (q_m=0 and ω_b=0) as the experiments were performed ex vivo.

The electrical and thermal properties of the tissue and electrode are shown in Table 2. For the σ (T) of the liver, an increase of 2%/ °C was used in accordance with Schwan and Foster [12]. For tissue temperatures exceeding 100°C, the electrical conductivity was assumed to drop by a factor of 10000 to simulate tissue dissection as done previously by Haemmerich et al. [13]. It has been previously shown that other parameters within the model are also temperature tissue dependent, specifically k and c [14,15]. However, the effects were small in comparison to that of σ (T) and were not considered in this model in order to reduce computational time [9].

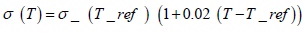(2)

Table 2: Thermal and electrical material properties used in the FEM.

Fem simulation setup: ABAQUS software was used to simulate the working process of the electrode hook. The software allows users to create the geometric model, assign material properties to the appropriate regions, as well as to specify the boundary conditions and loads. ABAQUS is also capable of solving the bioheat equation (1). A schematic of FEM for this study is shown in Figure 2. In the finite element analysis, we compared two different electrode geometrical designs, both of which are coated. The geometry of the electrodes is shown in Figure 2a. The electrode hook embedded in the tissue is illustrated in Figure 2b. The electrode hook and tissue were generated using linear coupled thermal-electrical elements by Abaqus. The mesh refinement feature was used to create a finer mesh in regions near the electrode where electrical and temperature information was critical. The mesh of electrode and tissue is shown in Figure 2c.

The thermal boundary condition for the surfaces of the tissue not contacting an electrode was set at a constant temperature T₀, which was equal to 25°C in this study. Convection was assumed for all exposed surfaces of the tissue. In this study, a convection coefficient of 25 W/m²K was utilized [16]. The initial condition for temperature was T₀= 25°C for all simulations with the ambient temperature.

Modeling the ac voltage is typically performed by converting the signal to a dc voltage by calculating its root mean square (RMS). A voltage equal to the experimental RMS voltage was applied on the top surface of the electrode. The total simulation time was 3s which was the same as the experiment. From the simulation, the calculation results of the electric field and temperature field were obtained through simulation to compare with the experimental results.

In vivo acute study

The live porcine model was used to mimic the conditions encountered within the clinical environment because the anatomical and physiological characteristics are similar to humans. The in vivo acute test focused on investigating the lowest power setting for smooth cutting on mesentery by using different devices (Figure 3).

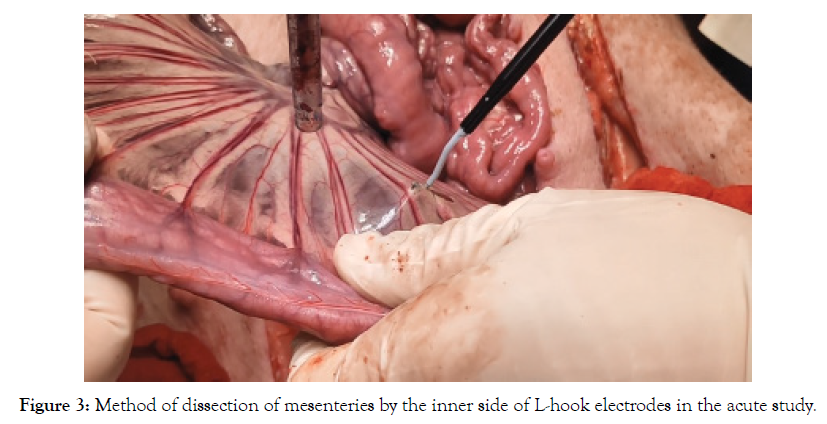
Figure 3: Method of dissection of mesenteries by the inner side of L-hook electrodes in the acute study.

One porcine model was used in the acute study. The animal underwent standard surgical preparation and positioning for exploratory laparotomy. The animals were placed in a dorsal recumbent position with hair clipped from the mid-chest to the pubis. A midline celiotomy was performed to expose the viscera and small bowel mesentery. We dissected small bowel mesentery in fulgurate mode with the inside edge of the different designs. To obtain the optimal lowest power setting for each device, the cut was performed starting from 10 watts in fulgurate mode with adding 5W gradually for both the novel design and CleanCoat™ based on previous experience. After we obtained the optimal lowest power setting, 10 centimeters of the mesentery was cut to verify the smooth cutting.

The animal used in this study was pre-medicated and maintained under anesthesia according to the test facility’s standard operating procedures. IV infusion was given continuously at a minimum required rate during surgery. At the conclusion of the session, the animal was euthanized according to the test facility’s standard operating procedures.

Statistical analysis

Statistical analyses were conducted using a 2-sample t-test, and calculations were performed using Minitab^®18 software. All p-values were two-sided, and the significance was set at p<0.05.

Results

Pulling force test configurations were set at the same mode, power setting, angle, cutting speed, and tissue as listed in Table 3. The test results showed that the pulling force in the novel design wire was 2.938 ± 0.795 N, which was significantly lower than that in the CleanCoat™ wire (12.857 ± 4.189 N), the pulling force in the novel design (7.025 ± 3.845 N) flat was significantly lower than that in the CleanCoat™ flat (15.257 ± 2.988 N) as well (Table 4 & Figure 4).

Table 3: Settings for pulling force test.

Table 4: The test results of pulling force of wire and flat L-hooks.

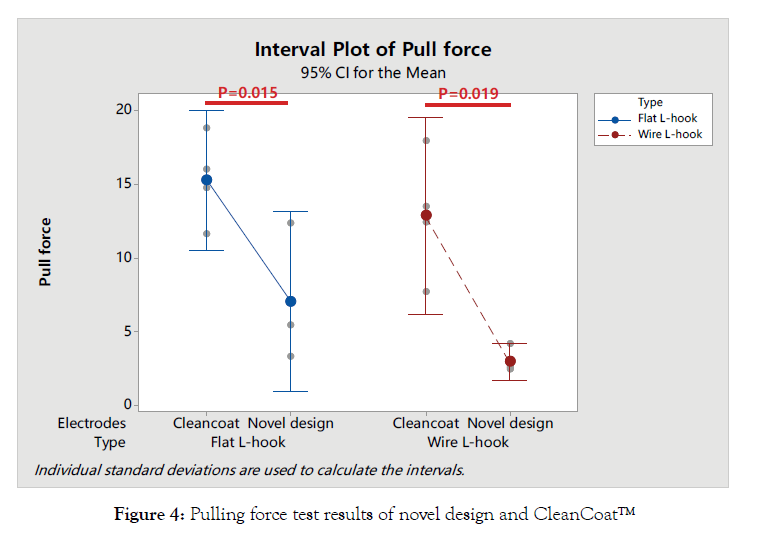
Figure 4: Pulling force test results of novel design and CleanCoat™

Simulation analysis evaluation

Figure 5a shows the comparison of electric field simulation results of the two different electrodes. The simulation results showed that the maximum current density of the novel design was 0.047 A/ mm², and the maximum current density of CleanCoatTM was 0.028 A/mm². These results suggested the cutting force of the novel design was smaller at the same power. This observed test result was consistent with the previous experimental results. Figure 5b shows the comparison of temperature field simulation results of the two different electrodes. The upper limit temperature for tissue thermal damage was set at 80°C, and the area above 80°C was gray in color. It was clear from the figure that the gray area of the novel design is much smaller than that of CleanCoat™, indicating less thermal damage caused by the novel design at the same power.

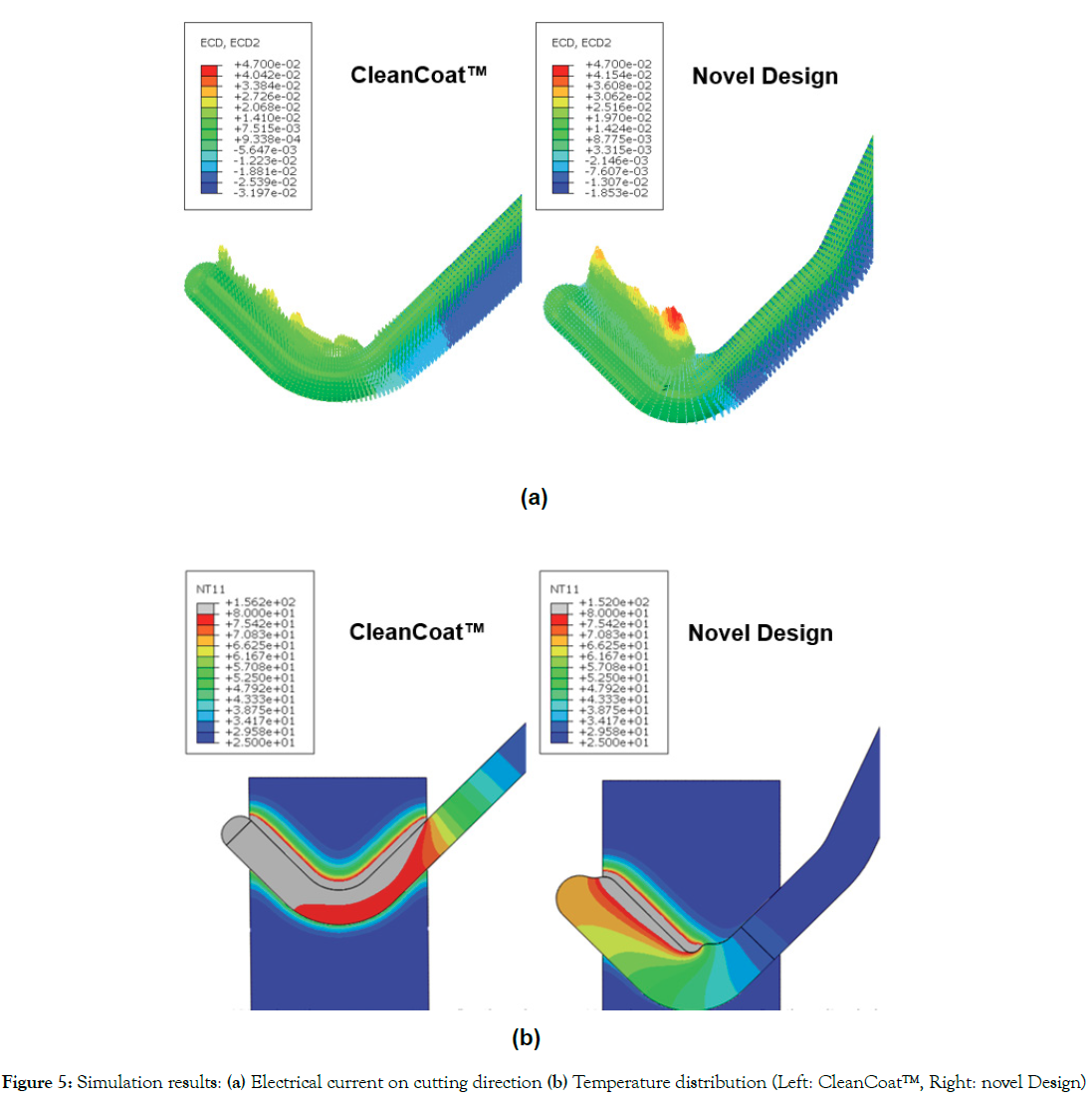
Figure 5: Simulation results: (a) Electrical current on cutting direction (b) Temperature distribution (Left: CleanCoat™, Right: novel Design)

Acute animal experiment

In the acute porcine model, the lowest power setting for performing cut in mesentery is shown in Table 5. The cutting could be performed using the novel design at the power setting 20W for both wire and flat, while with the CleanCoat™, the lowest power setting for wire and flat were 30W and 35W respectively, which was consistent with simulation and pulling force results.

Table 5: The lowest power setting of electrodes when dissecting in the acute study.

Discussion

The principle of the laparoscopic electrode hook is to use the highfrequency energy released by the electric surface to dissect the tissue. Currently, the goal of the laparoscopic electrode hook design is to optimize the cutting efficiency at a set power, thereby reducing the thermal damage in the surgeries, which is the main concern during the procedure [5,6]. Under the same energy output, the size of the contact surface area between the L-Hook electrode and the tissue has a decisive relationship with the current density and thus affects the clinical effect [17].

In this study, we compared the pulling force difference between CleanCoat™ hook and the novel design which added an edge on the inner side of the original design to reduce the contact area. The result of the pulling force test system showed the pulling force of the novel design was s significantly lower than that of the original design, consistent with the simulation analysis and the animal test. Additionally, the simulation evaluation indicated lower temperature damage associated with the novel design dissection, which could be beneficial for patients.

Conclusion

Verification and validation are independent procedures that are used together for checking whether a product, service, or system meets the requirements and specifications and whether it fulfils its intended purpose [18-20]. Our study combined the verification method including the pulling force test and simulation analysis and validation in the animal lab. The ex vivo pulling force system and the simulation analysis in our study could minimize the measurement variability while the in vivo experiment could maximumly simulate the real clinical practice and validate the outcomes from ex vivo studies. This comprehensive method can ensure the testing results to be accurate, authenticated, and practical for the application of the device in clinical settings. Therefore, this method will be a valuable tool to explore the lowest power setting to optimize the dissection performance of laparoscopic electrode hooks in future medical device development.

Ethical Statement

All procedures in this study involving animals were in accordance with the ethical standards of the institutional and/or national research committee. Approval was obtained from Institutional Animal Care and Use Committee (IACUC) of Medtronic Innovation Center (MIC) and Science and Technology Commission of Shanghai Municipality.

Acknowledgement

The authors would like to acknowledge Zaifeng Zhou, Kelyn Bonn, Xinmeng Liu, Tong Shen, Yongming Zhao for their contributions to this study.

References

1. Hainer BL. Fundamentals of electrosurgery. J Am Board Fam Pract. 1991;4(6):419-426.
2. Wallwiener CW, Rajab TK, Kramer B, Isaacson KB, Brucker S, Wallwiener M. Quantifying electrosurgery-induced thermal effects and damage to human tissue: an exploratory study with the fallopian tube as a novel in-vivo in-situ model. J Minim Invasive Gynecol. 2010;17(1):70-77.
3. Družijanić N, Pogorelić Z, Perko Z, Mrklić I, Tomić S. Comparison of lateral thermal damage of the human peritoneum using monopolar diathermy, Harmonic scalpel and LigaSure. Can J Surg. 2012;55(5):317-321.
4. Diamantis T, Kontos M, Arvelakis A, Syroukis S, Koronarchis D, Papalois A, et al. Comparison of monopolar electrocoagulation, bipolar electrocoagulation, Ultracision, and Ligasure. Surg Today. 2006;36(10):908-913.
5. Sutton PA, Awad S, Perkins AC, Lobo DN. Comparison of lateral thermal spread using monopolar and bipolar diathermy, the Harmonic Scalpel and the Ligasure. Br J Surg. 2010;97(3):428-433.
6. Hefermehl LJ, Largo RA, Hermanns T, Poyet C, Sulser T, Eberli D. Lateral temperature spread of monopolar, bipolar and ultrasonic instruments for robot-assisted laparoscopic surgery. BJU Int. 2014;114(2):245-252.
7. Buia A, Stockhausen F, Hanisch E. Laparoscopic surgery: A qualified systematic review. World J Methodol. 2015;5(4):238.
8. Jiang HP, Liu YD, Li YS, Shen ZL, Ye YJ. Ultrasonic versus electrosurgical device for laparoscopic cholecystectomy: A systematic review with meta-analysis and trial sequential analysis. Int J Surg. 2017;40:24-32.
9. Dodde RE, Miller SF, Geiger JD, Shih AJ. Thermal-electric finite element analysis and experimental validation of bipolar electrosurgical cautery. J Manuf Sci e-t Asme. 2008;130(2).
10. Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol. 1948;1(2):93-122.
11. Berjano EJ. Theoretical modeling for radiofrequency ablation: state-of-the-art and challenges for the future. Biomed. 2006;5(1):1-17.
12. Schwan HP, Foster KR. RF-field interactions with biological systems: Electrical properties and biophysical mechanisms. Proceedings of the IEEE. 1980;68(1):104-113.
13. Haemmerich D, Chachati L, Wright AS, Mahvi DM, Lee FT, Webster JG. Hepatic radiofrequency ablation with internally cooled probes: effect of coolant temperature on lesion size. Ieee Trans Biomed Eng. 2003;50(4):493-500.
14. Valvano J, Allen J, Bowman H. The simultaneous measurement of thermal conductivity, thermal diffusivity, and perfusion in small volumes of tissue. 1984.
15. Madsen K, Nielsen HB. Introduction to optimization and data fitting, 2008.
16. Liang P, Dong B, Yu X, Yu D, Cheng Z, Su L, et al. Computer-aided dynamic simulation of microwave-induced thermal distribution in coagulation of liver cancer. IEEE Trans Biomed Eng. 2001;48(7):821-829.
17. Boosari SSH. Predicting the dynamic parameters of multiphase intelligence-(Cascading Deployment). Fluids. 2019;4:44.
18. Incropera FP, Lavine AS, Bergman TL, DeWitt DP. Fundamentals of heat and mass transfer: 2007.Higuera P, Lara JL, Losada IJ. Three-dimensional interaction of waves and porous coastal structures using OpenFOAM®. Part I: Formulation and validation. Coast Eng. 2014;83:243-258.
19. Messenger D, Carter F, Francis N. Electrosurgery and energized dissection. Surgery. 2014;32(3):126-130.
20. Fries RC. Medical device quality assurance and regulatory compliance: Boca Raton, Florida, USA. 1998.