International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2017) Volume 8, Issue 4
Timber utility poles play a significant role in the infrastructure of Australia as well as many other countries for power distribution and communication networks. Due to the advanced age of Australia’s timber pole infrastructure, substantial efforts are undertaken on maintenance and asset management to avoid any failures of the utility lines. Nevertheless, the lack of reliable tools for assessing the condition of in-service poles seriously jeopardizes the maintenance and asset management. For instance, each year approximately 300,000 poles are replaced in the Eastern States of Australia with up to 80% of them still being in a very good condition, resulting in major waste of natural resources and money. Non-destructive testing (NDT) methods based on stress wave propagation can potentially offer simple and cost-effective tools for identifying the in-service condition of timber poles. Nonetheless, most of the currently available methods are not appropriate for condition assessment of timber poles in-service due to presence of uncertainties such as complicated material properties, environmental conditions, interaction of soil and structure, and an impact excitation type. In order to address these complexities, advanced digital signal processing methodologies are needed to be employed. Deterministic signal separation, blind signal separation, and frequency-wavenumber velocity filtering are the three groups of methodologies, which could most probably provide solutions. In this paper applicability and effectiveness of the blind signal separation methods is investigated through a numerical data obtained from of a timber pole modelled with both isotropic and orthotropic material properties. Principal Component Analysis (PCA), Singular Value Decomposition (SVD), and K-means clustering algorithms are the blind signal separation methodologies that are employed in this research work.
<Keywords: Timber pole; Structure health monitoring; Nondestructive testing; Signal processing; Blind signal separation; Condition assessment
Timber utility poles play a significant role in the infrastructure of Australia as well as many other countries. There are over 5 million timber utility poles currently used in Australian energy networks, which are more than 80% of total utility poles in the network. Due to the advanced age of Australia’s timber pole infrastructure, substantial efforts are undertaken by state authorities on maintenance and asset management to prevent utility lines from failure [1]. However, the lack of reliable information regarding their in-service condition, including the embedment length makes it really difficult for the asset managers to make decisions on the replacement/maintenance process with due consideration to economy, operational efficiency, risk/liability and public safety. For example, in order to avoid any failure and considering the public safety, each year approximately 300,000 poles are replaced in the Eastern States of Australia with up to 80% of them still being in a very good serviceable condition, resulting in significant waste of natural resources and money.
Non-destructive testing (NDT) methods based on stress wave propagation can potentially offer simple and cost-effective tools for identifying the in-service condition of timber poles. Stress waves can be generated as a result of deformations caused by impact excitation. The propagation of the stress waves depends on the geometry of the structure as well as its material properties such as the modulus of elasticity, Poisson’s ratio, and density. Since timber is an orthotropic material by nature, the wave propagation in longitudinal, tangential, and radial directions differs. In this regard, analysing captured impulse response signals from a timber pole can provide hints on the structure’s soundness. It is also worthy to mention that the captured signals include many reflections, which are produced by the timber pole boundaries, any damage inside, top and bottom of the pole, and in the case of lateral impact up- and downward travelling waves.
Most of the currently available NDT methods are not suitable for condition assessment of timber poles in-service due to presence of uncertainties such as complicated material properties and imperfect body (i.e., timber pole natural cracks), environmental conditions, interaction of soil and structure, defects and deteriorations as well as an impact excitation type. It is necessary to mention that access to the top of the in-service timber utility poles is prohibitive due to the presence of the electrical or communication wires. In this regard, the hammer impact is applied to the timber pole on its side.
In order to address all mentioned complexities, advanced digital signal processing methodologies are needed to be employed. From the signal processing point of view, in order to be able to assess the condition of the timber pole, several existing reflections in the captured signals are needed to be separated first. Deterministic signal separation, blind signal separation, and frequency-wavenumber velocity filtering are the three groups of methodologies, which could most probably provide solutions. The effectiveness and the applicability of the deterministic signal separation methods as well as frequencywavenumber velocity filtering were studied in our previous work [2]. In this paper applicability and effectiveness of the blind signal separation methods in separating the existing patterns in the captured signals from the timber utility pole is investigated. Principal Component Analysis (PCA), Singular Value Decomposition (SVD), and K-means clustering algorithms are the blind signal separation methodologies that are employed in this paper. The structure of the paper is as follows. In section 2, a review of the employed blind signal separation methods as well as the test structure are explained. In section 3, results of employing aforementioned signal processing techniques are provided. Discussion on the obtained results as well as more detailed explanations of the results obtained from the deterministic signal separation methods are also provided in this section. Finally, conclusion of this paper and suggestions for the future works are provided in section 4. Main contribution of this paper is illustrating the complexities exist in the condition assessment of the timber pole. These complexities are due to the presence of uncertainties such as complicated material properties and imperfect body (i.e., timber pole natural cracks), environmental conditions, interaction of soil and structure, defects and deteriorations as well as an impact excitation type. Due to the presence of the electrical or communication wires, the hammer impact is applied to the timber pole on its side. Furthermore, in this paper the effects of simulating the timber pole with both isotropic and orthotropic material properties on the applicability of the blind signal separation methods are also investigated.
Blind Signal or Source Separation refers to a group of unsupervised signal processing techniques in which the input signal or any information about it is not available [3]. In these methods, the system is assumed to be multi input multi output [4], which means that N signals are produced by different sources, these signals are then captured by M sensors after travelling through the medium. Based on the statistical differences, blind signal separation methods can separate the signals from all sources having only signals captured by the sensors. In this regard, firstly a data matrix of M*N is made with observations in the columns and different sensors in the rows, then the blind separation methods can be applied on this data matrix in order to separate the source signals. The main algorithms that are used in this paper are Principal Component Analysis, Singular Value Decomposition, which do not involve any learning algorithm, and k-mean clustering algorithm, which contains a learning algorithm.
Principal component analysis
Principal Component Analysis (PCA) or discrete Karhunen–Loève transform (KLT) is a mathematical process which transfers observations (data) that are possibly correlated, into a set of orthogonal values (features) which are linearly correlated and called principal components; this method is based on the second order statistics (covariance). Data has the most variance over the first principal component (which means that this component represents the most correlated and important feature of the data), while over the last component data has the smallest variance which means it is the most uncorrelated feature of the data (can be assumed as white noise) [3,5]. PCA can be mathematically expressed as follows. Firstly a data matrix (A) of M*N is made with observations in the columns and different sensors in the rows. Then the covariance matrix will be calculated using equation (1).
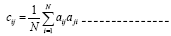 (1)
(1)
Where c and a denote each component of the covariance and dataset matrices. Writing the equation (2) in the matrix form gives:
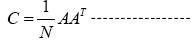 (2)
(2)
Often the scale factor 1/N is distributed throughout the matrix and the covariance matrix is written simply as AAT. The eigenvalues of the covariance matrix represent the principal components, while the eigenvectors represent the orthogonal axes in the transferred domain. Some of the applications of the PCA in civil engineering area can be found [6,7].
Singular value decomposition
Singular value decomposition (SVD) is a matrix factorization process in which M*N matrix, will be decomposed into three matrices by equation (3).
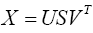 (3)
(3)
Where U and V are M*M and N*N unitary matrices, and S is M*N rectangular and diagonal matrix which holds the singular values (same as principal components in the PCA). Columns of U and V are called left and right singular vectors [8,9].
Equation 3 can be rewritten in terms of summation of the each singular value multiplied by its related left and right singular vectors. This is shown in equation (4).
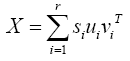 (4)
(4)
Where the factor uivi T is an M*N matrix and called the ith eigenimage of the data matrix. SVD has been applied in many massively in the civil engineering field; Freire et al. [10] applied SVD to separate downgoing waves (first arrivals to sensors) from up-going waves (reflections and multiples) in vertical seismic profiling. They also used this method for the noise attenuation [10]. Vrabie et al. applied the combination of SVD and ICA in order to obtain better source (signal) separation in terms of better sensor to sensor correlation [11]. Vrabie VD et al. [12] introduced three-dimensional SVD; they assumed the data as dimensions of the time, sensor numbers, and the sensor directions.
K-mean clustering [13]
The term K-means clustering was first mentioned by James MacQueen in 1967 [14]. This method aims to categorize N observations into K groups or clusters. It starts by choosing K points as the initial centroids for all clusters. Then each point in the dataset is assigned to the closest centroid based on a particular proximity measure chosen. Once the clusters are formed, the centroids for each cluster are updated. The algorithm then iteratively repeats these two steps until the centroids do not change or any other alternative relaxed convergence criterion is met. Figure 1 demonstrates the K-mean algorithm flowchart [13].
Several proximity measures can be used within the K-means algorithm for splitting the data set into K groups such as Manhattan, and Euclidean distance, or Cosine similarity. In general as well as this work, the Euclidean distance metric is used for the K-means clustering. It is essential to consider that different values of K and proximity measures can significantly affect the final output. The objective function, which is employed by K-means as a convergence criterion, is called the Sum of Squared Errors (SSE) or Residual Sum of Squares (RSS). The mathematical formulation for SSE/RSS is as follows:
Given a dataset A= {X1,X2,...,XN} consists of N points, the clusters obtained after applying K-means clustering can be denoted by C= {C1,C2,...,Ck,...,CK}. The SSE for this clustering is defined in the Equation (5), where ck is the centroid of the cluster CK [13].
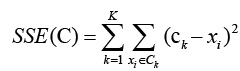 (5)
(5)
The iterative assignment and update steps of the K-means algorithm aim to minimize the SSE function for all of the clusters. In the following, Mathematical procedure of minimization of the SSE and also a proof of the reason behind choosing the mean of the data points in a cluster as the prototype representative for a cluster in the K-means algorithm are provided. Here, Ck and ck represent the kth cluster and its mean, and xi is a point in the kth cluster. The SSE function can be minimized by its differentiating with respect to cj and setting it equal to zero as shown in equation (6).
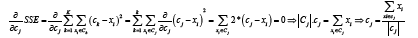
Based on the equation (3.19), the best descriptive for minimizing the SSE function of a cluster is the mean of the points in the cluster. In the K-means, the SSE value consistently decreases on each of the iterations. This monotonically decreasing behaviour will eventually converge to a local minimum [13].
K-mean clustering is one of the most frequently applied blind signal separation (or clustering) methods in a variety of fields especially in engineering and NDT. For instance, Yousefi et al. have applied the K-mean clustering algorithm on the signals obtained from the acoustic emission to extract a general pattern of a specific damage on a glass/epoxy composite material [15]. Crivelli et al. combined the K-mean algorithm with the Artificial Neural Network (ANN) for damage detection and real-time structural monitoring of a composite lightweight material [16]. Ihesiulor et al. also utilized K-mean algorithm and ANN for a delamination prediction in laminated composite structures [17]. Some other applications of the K-mean clustering algorithm in engineering, and NDT can be found [18-22].
The test structure
To investigate the effectiveness of the proposed methods, they were applied to finite element (FE) models of a timber pole. The numerical models were created and analysed with the software ANSYS using transient analysis. The modelled poles were 11 m or 12 m long and had a diameter of 300 mm, which are typical dimensions of utility poles used in the field. An impact force, generating stress waves, was applied to the surface of the pole at a location 3 m above the pole bottom and with an impact angle of 45°. The impact load was similar to a hammer impact typically executed in field testing. The impact response of the pole structure was captured along the pole at 241 locations (with a spacing of 0.05 m), with the first measurement point being located at the bottom and the last at the top of the pole. To test the proposed algorithm, the following two timber pole cases were modelled and analysed:
(a) Timber pole modelled with isotropic material properties with1.5 m soil embedment.
(b) Timber pole modelled with orthotropic material properties with 1.5 m soil embedment.
For the isotropic modelling of the timber, material properties are as follows: the density (ρ) was set to 950 kg/m3, the elastic modulus (E) to 23,000 MPa, and the Poison’s ratio (v) to 0.3. For the orthotropic modelling material properties in Tables 1 and 2 were used. The material properties of the soil are ρ=1,520 kg/m3, 100 MPa, and v=0.3.
| Radial Direction | Transversal Direction | Longitudinal Direction | |
|---|---|---|---|
| Elastic modulus (MPa) | 1955 | 850 | 23000 |
Table 1: Elastic modulus values of simulated orthotropic timber pole.
| Radial Transversal | Transversal Longitudinal | Radial Longitudinal | |
|---|---|---|---|
| Shear Modulus (MPa) | 357 | 1037 | 1513 |
| Poison’s ratio | 0.682 | 0.023 | 0.044 |
Table 2: Shear modulus and Poisson’s ratio values of simulated orthotropic timber pole.
As mentioned earlier, several reflections exist in the captured signals. These reflections can be caused mainly by timber pole boundaries, its top and bottom, and damages or natural cracks inside. The interference between these reflections makes the condition assessment impossible since for a specific purpose, true reflection peak cannot be detected (e.g. if the embedment length is the purpose, the peak related to the reflection from the bottom of the pole cannot be detected in its correct time due to the interference). In this regard, the applicability and effectiveness of the proposed blind signal separation methodologies on separating the patterns related to the aforementioned reflections are provided in this section. The effectiveness of each methodology is investigated on the simulated timber pole with isotropic and orthotropic material properties.
PCA
Figure 2 illustrates the principal components of the simulated isotropic timber pole with the embedded in 1.5 m soil condition.
First eight most important principal components are used for reconstruction of the signals back into the time-space domain. Figure 3 shows the original signals, the signals that transferred back to the time-space domain by using the first eight most important principal components, and the reconstructed signals using the rest of the principal components. As can be seen in Figure 3, the PCA could noticeably clear the signal and highlight the main patterns of the signal. It is essential to consider that since the statistical properties of both of the upward and downward travelling waves are the same, and the PCA is based on the covariance matrix, both of these waves are categorized in the same group in the principal components domain. In other words, the PCA is not able to separate the upward and downward travelling waves from each other, but it can clear the signals from the rest of the unwanted patterns.
Figure 4 shows the principal components of the simulated orthotropic timber pole with the embedded condition.
The first eight principal components have been used to transfer the signal back to the time-space domain, which are shown in Figure 5.
It can be seen in Figure 5 that for the simulated orthotropic timber pole with the embedded condition, the PCA cannot clear the signals. This is due to the changes of the existing statistical properties in the captured signals. The changes in the statistical properties are due to the effects of the dispersion caused by the orthotropic material properties of the timber pole, which will be explained shortly.
SVD
Figure 6 shows the Singular values of the simulated isotropic timber pole with the embedded condition.
In the SVD, the singular values can be separated in three groups of low, medium, and large. The most important singular values are grouped in the low, while the less important ones are grouped as the high, and the ones in the middle are grouped as the medium. The first ten singular values are grouped as the low, ten to thirty are grouped as the medium, and the rest are in the high group. Figure 7 illustrate the time-space domain signals, which are obtained from each of these groups of the singular values.
It can be seen in Figure 7 that the SVD could highlight the main patterns and remove the noise. Since the statistical properties of the up- and downward travelling waves are the same, SVD is not effective in separating of these travelling waves from each other.
Figure 8 demonstrates the singular values of the simulated orthotropic timber pole with the embedded condition.
In this case, only the first five singular values are grouped as low, from five to thirty are grouped as medium, and the remaining are grouped as the high ones. Figure 9 illustrates the time signals obtained from each of these groups of the singular values.
It can be seen in Figure 9 that the SVD could not preserve the main patterns as it did in the isotropic case. The SVD and the PCA are both based on second order statistics. In fact, the distortion caused by the orthotropic material properties of the timber pole and the impact type makes it impossible for the algorithms like PCA and SVD to separate the existing patterns in the signal from each other. In the situation where the timber pole is simulated with the isotropic material properties, these algorithms can only remove the noise and are not able to separate the patterns with the similar statistical properties like the upward and downward travelling waves from each other.
K-mean clustering
In this section, K-mean clustering, which is the iterative and learning algorithm, is employed on the data captured form the simulated orthotropic timber pole in order to deal with the intrinsic complexities exist in the data and to separate the different patterns from each other. One of the major steps in the learning algorithms is a feature extraction. Feature extraction is needed to be done in a way to assure that the most convenience features of the data are fed into the learning algorithm. As mentioned earlier, the captured signals from the simulated orthotropic timber pole as well as real timber pole suffer heavily from the dispersion. On the other hand, dispersion relation can be obtained from the temporal (well-known frequency) and the spatial (knows as wavenumber) frequency relations (the propagation equations are solved for the temporal frequencies, while the roots are spatial frequencies). Two-dimensional Fast Fourier Transform (FFT) of the two dimensional data (captured signals from 241 sensors) can obtain the data in the two dimensions of the temporal and spatial frequency domains. Since the dispersion relation is obtained directly from the aforementioned transferred data, this data is also used to feed to the K-mean clustering algorithm. Original data (that is going to be fed into the algorithm) is shown in Figure 10.
It is necessary to consider that since one-dimensional FFT is mirrored in the frequency domain, two-dimensional FFT has four mirrored sections. For this reason, only one quarter of the transferred data (shown by the rectangular in Figure 10) has fed into the K-mean algorithm, and the outputs are generalized into the other three sections. In this regard, K-mean algorithm is set in a way that it separates its input dataset into the five clusters. The result of the K-mean clustering is shown in Figure 11.
Figure 11 demonstrates the Silhouette value of each cluster vs. the related cluster. As can be seen, third cluster is the most important cluster amongst all five, and its silhouette value is one. The related data of the third cluster in the F-K (Frequency-Wavenumber) domain (which obtained from the K-mean algorithm) that contains the desired output is shown in Figure 12.
Figure 13 illustrates the original signals and the K-mean clustering outputs in the time-space dimensions. As can be seen in Figure 13b, the K-mean clustering could successfully separate the longitudinal and the bending waves from each other.
Figure 13: (a) Original data captured from the simulated orthotropic timber pole after low-pass filtering with 4500 Hz (Hammer impact frequency range); (b) the data of the third cluster which is transferred back to the time-space domain; (c) the data obtained from the rest of the clusters which is transferred back to the time-space domain.
Figure 14 shows the outputs of the K-mean clustering followed by the predictive deconvolution (Predictive deconvolution is used for separation of the up- and downward travelling waves, details of the methodology can be found in [2]). It can be seen in this figure that although the predictive deconvolution could remove the downward travelling wave, it weakened or in some sensors remove the reflection peaks (especially in sensors near the soil). The very weak detected reflection peaks are used for the velocity analysis and the embedment length estimation.
The velocity analysis procedure for the sensors that are shown with the oval in Figure 14 is illustrated in Figure 15. These sensors are chosen based on the real in-field sensors locations (in real in-field tests, only eight sensors are attached to the pole starting from the ground level with 0.2 m distance).
It can be seen in Figure 15 that although the estimated velocity of the down-going wave is in expected range, the velocity of the reflection wave is enormously higher than the usual. In fact, although the K-mean algorithm could successfully separate the longitudinal waves and the bending waves from each other, due to the interference between the existing branches, results of the velocity analysis are not reliable. It can be seen that the estimated velocity after applying the predictive deconvolution will be around the unrealistic value of 14000 m/s. In the following, possible reasons of such distortion caused by the orthotropic nature of the timber pole are explained.
Hammer impact excites the timber pole in the broad range of frequencies (0-5 kHz). If all of the frequencies propagate through the timber pole with the same velocity, shape of the signal will not change through the propagation period. This means that the statistical properties of the several existing patterns will not change. On the other hand, if different frequencies travel with different velocities, the overall shape of the signal will change. In other word, the existing statistical properties will change. This phenomenon is known as dispersion effect. Considering the cylindrical timber pole, dispersion relations for the simulated isotropic and orthotropic timber poles are shown in Figure 16. As can be seen in Figure 16a, the simulated isotropic timber pole acts as the non-dispersive medium in the frequency range of 0-7 kHz (i.e., in this frequency range the group velocity and the phase velocities are relatively the same). Consequently, the simulated isotropic timber pole acts as a non-dispersive medium under the hammer impact load. This is the main reason that the main patterns related to the up- and downward travelling waves could easily be detected in the isotropic case.
Figure 16: Dispersion curves of the cylindrical timber poles in (a) the isotropic; and (b) the orthotropic cases. Dashed lines represent the flexural wave branches and hard lines represent the longitudinal branches [23].
On the other hand, the simulated orthotropic timber pole (which is more similar to the reality) is highly dispersive material in the frequency range of 0-5 kHz (the hammer impact frequency range). Furthermore, lateral hammer impact with 45° angle excitation creates both longitudinal and the bending waves simultaneously, while each of them has at least two branches in this frequency range. The situation is worse when each of mentioned branches has a highly nonlinear behaviour.
By looking at Figure 16b, one can simply see that five branches exist in the frequency range of the hammer impact. Considering Figure 16b, if the timber pole is excited with the broadband frequency impact (i.e., hammer), the captured signals suffer from severe distortions. These distortions are related to firstly the nonlinear behaviour of each of the branches (longitudinal and bending), secondly to the interference or the contributions between these branches in the hammer excitation frequency range. It is worth considering that when different frequencies travel with different velocities, each of the frequency components has its own reflection (e.g. from the bottom of the pole), while the interference between the reflections created in the single and the same frequency but from the different modes can result in the peaks removal in the captured signal.
Timber pole is an orthotropic material by nature. In this regard, its behaviour under the lateral 45° hammer impact excitation is very complicated and captured signals suffers from severe distortions. It is shown in this paper that since the simulated timber pole with an isotropic material properties acts as a non-dispersive medium in the hammer impact excitation frequency range, main patterns related to the up- and downward travelling waves can be preserved by the PCA and SVD, while these patterns could not be separated from each other due to their same statistical properties. It is also shown that these algorithms are not effective on the captured signals from the simulated timber pole with the orthotropic material properties due to the dispersion effects. In this regard, K-mean algorithm, which is an iterative and learning algorithm, has been modified and employed for separation of existing patterns in the captured signals. The results, however, demonstrated that although it could successfully separate the longitudinal waves from the bending ones, the interference between existing branches was not amendable and led to unrealistic and unreliable results.
Main contributions of this paper are as follows. Firstly, to illustrate the difference between isotropic and orthotropic simulations of the timber poles from the signal processing point of view, and also the effects of simplifications in the isotropic simulations. Secondly and mainly, to demonstrate the high level of complexities that exist in the processing of the captured signals when the timber pole is excited with the lateral 45° broadband frequency range impact (i.e.,hammer). In fact, if dealing with high level of complexities is not impossible, it is a very difficult task. In this regard, the authors strongly recommend not exciting the timber pole in a broad range of frequencies especially when the impact is applied on the side of the structure with an angle. In fact, exciting the timber pole with a narrowband impact excitation makes a less complicated situation. Furthermore, for damage detection purposes, it is recommended not to use low frequency ranged because of “th” large time lengths of the waves.