Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 3
This paper examines the idiosyncratic volatility puzzle and whether investor sentiment influences the relation between idiosyncratic volatility and stock returns in the Chinese stock market. The findings indicate the existence of a negative idiosyncratic volatility effect. In addition, the results show that the relation between idiosyncratic volatility and returns significantly depends on investor sentiment. Thus, investor sentiment plays a very important role in reconciling the relation between idiosyncratic volatility and stock returns in the Chinese stock market. This implies that investor sentiment may be one of the major risk factors that should be considered in the Chinese stock market. In terms of predictive ability of investor sentiment, idiosyncratic volatility and market volatility, the findings indicate that idiosyncratic volatility positively predicts future excess market returns in the Chinese stock market.
<Keywords: Idiosyncratic, Chinese, Stock market, Investor, Puzzle
Recent empirical studies have found a cross-sectional relation between idiosyncratic volatility and expected stock returns. Some previous studies suggest either a positive [1-8] or an insignificant [9,10] relationship between idiosyncratic volatility and expected returns. In contrast, recent work by Guo et al. [11-13] find that idiosyncratic volatility is negatively related to returns. Similarly, Nartea [7] also find evidence of a negative idiosyncratic volatility effect in China supporting the findings of Ang [11]. These relationships exist because investors cannot fully diversify their stock portfolios suggesting that idiosyncratic volatility should be priced. Capital asset pricing model, on the other hand, indicates that only systematic risk should be priced because idiosyncratic risk can be diversified away when investors hold a well-diversified portfolio of stocks.
In addition, classical finance theory argues that asset prices are not influenced by investor sentiment, because rational investors are ready to offset any asset mispricing. In other words, rational investors set the prices of assets in the market and therefore there is no role for investor sentiment. This view of rational investors is based on fundamental reasons and investor sentiment is perceived as being out of touch with reality and is generally defined as excessive optimism or pessimism about the market’s prospects that is caused by investors’ erroneous beliefs about prices that are not justified by fundamentals. However, recent empirical studies report that investor sentiment has an effect on expected stock returns [14-18]. This suggests that the asset price errors cannot be canceled out by rational arbitrageurs due to the limits of arbitrage [19,20]. Consequently, investor sentiment should be considered as a determinant risk factor in the asset pricing model.
Empirical studies by Baker and Jeffrey, Brown et al., Kumar and Lee [14-16] and Hvidkjaer [21] attribute the relation between investor sentiment and future returns to investor optimism that drive prices above fundamental values or investor pessimism that drive prices below fundamental values. Thus, overvaluation is an indication of investor optimism and undervaluation shows investor pessimism. It is established that both rational and sentiment investors could be either optimistic or pessimistic about the market’s prospects. The theory, on the other hand, assumes that rational investors always form correct expectations about the future value of an asset, whereas, sentiment investors consistently make errors in judgment contributing to overestimation or underestimation of asset prices, depending on their sentiment, leading to a divergence of prices from the fundamental values, thus creating mispricing in the market. However, the classical finance theory asserts that even if some investors are irrational, their demands are neutralized by the actions of rational arbitrageurs and consequently have no significant influence on prices [14].
Investor sentiment has become more important in situations where retail investors dominate the stock market, for example, the emerging stock markets. Han and Kumar [22] argue that the idiosyncratic volatility puzzle is a characteristic in a market that is dominated by individual investors. It is generally accepted that retail investors add to the idiosyncratic volatility of stock returns because they act as noise traders. Noise traders are broadly retail investors who trade for reasons other than fundamental information relating to misperceptions of future returns. They have no fundamental knowledge about stock markets making it more risky for the arbitrager, and thus creating a noise effect on the stock market returns. Noise trading models such as those Shleifer and Summers [23,24] assert that investor sentiment contributes to the deviation of asset prices from their fundamental values due to the limits to arbitrage. In contrast, where institutional investors dominate the market, such as in developed stock markets, the risk associated with investor sentiment reduces. For example, Finter et al. [25] indicate that investor sentiment has little importance in the German stock market that has a low fraction of retail investors. This is an indication that investor sentiment has an impact on stock prices in the emerging stock markets [17].
Many previous studies have been conducted on the relation between idiosyncratic volatility and expected return, but little attention has been paid to reconcile the negative cross-sectional relation between idiosyncratic volatility and expected stock returns using the role of investor sentiment. Empirical studies on the impact of investor sentiment on the cross-sectional relation between returns and volatility have only emerged recently. For example, Jiang [26] suggest that the inverse relation between idiosyncratic volatility and stock returns is significantly driven by news about firms’ future returns. In addition, Barinov [27] explains why high idiosyncratic volatility leads to low future returns using real options and aggregate volatility risk. Others including [28,29] find that investor sentiment plays a role in reconciling the negative relation between idiosyncratic volatility and expected returns. This paper, like Gao et al. [28] and Chi et al. [29] differs from previous studies on the topic by using investor sentiment to understand the idiosyncratic volatility puzzle. Specifically, this paper contributes to the literature by examining the impact of investor sentiment on the relation between the idiosyncratic volatility and expected returns in the Chinese stock market.
The objectives of this paper are (i) to investigate the idiosyncratic volatility puzzle in China and (ii) to explore whether investor sentiment influences the relation between idiosyncratic volatility and expected stock returns.
The rest of this paper is structured as follows. Section 2 summarizes the related literature. Section 3 provides data description and methodology, followed by section 4 that presents empirical results. Section 5 concludes the paper.
Ang et al. [11] find that firms with high idiosyncratic volatility stocks earn low returns in the United States (known as the idiosyncratic volatility puzzle). Further evidence by Ang [11] using 23 international developed markets including the G7 countries also indicates that high idiosyncratic volatility stocks have low returns in each of these countries, therefore confirming this finding in an international context. Similarly, Nartea et al. [7] examine the relation between idiosyncratic volatility and expected returns in the Chinese stock market and find a negative relationship. The authors suggest that this negative relationship could be driven by investor preferences for high idiosyncratic volatility stocks, a symptom of possible risk-seeking behaviour. Guo and Savickas [13], using daily US stock market data from July 1962 to December 2002, find that idiosyncratic volatility is negatively related to future stock market returns. Similarly, Pollet and Wilson also using the US stock market quarterly data from 1963 to 2004, show that idiosyncratic volatility is negatively related to expected returns.
Fu [5], on the other hand, using exponential GARCH models and the US stock data from July 1963 to December 2006, finds a positive relation between idiosyncratic volatility and expected stock returns. Fu [5] provides evidence that the negative relationship in Ang et al. [11] can be explained by a short-term returns reversal of stocks with high idiosyncratic volatility. Jiang et al. [26] using quarterly data on the US market spanning from January 1974 to December 2002, assess whether the idiosyncratic volatility puzzle is related to the previously documented market anomalies in the literature. The study reports that the idiosyncratic volatility puzzle is generated by the information content about future returns. In addition, they also find a potential link between the idiosyncratic volatility puzzle and strategic corporate behavior in information disclosure. Thus, their evidence indicates that the idiosyncratic volatility puzzle is related to selective corporate disclosure and is significant among less experienced investors who do not have the knowledge or experience to fully understand selective disclosure of corporate information. Barinov [27], using the US stock market data covering the period between January 1986 and December 2012, finds that the idiosyncratic volatility effect is explained by aggregate volatility risk and growth options, as opposed to Ang et al. [11] who suggest that aggregate volatility risk cannot explain the idiosyncratic volatility effect.
Recent empirical studies find evidence that investor sentiment influences expected stock returns. More recently, Gao et al. [28] examine the role of investor sentiment in the idiosyncratic volatility puzzle in the US market and find that investor sentiment plays an important role in explaining the relation between idiosyncratic volatility and expected stock returns. Their results reveal that returns have a negative relationship with idiosyncratic volatility in a time series analysis. The findings also show that, during low sentiment periods, apparently no relation is observed between idiosyncratic volatility and expected stock returns, but reveal a strong negative relationship between idiosyncratic volatility and expected stock returns during periods of high sentiment suggesting that sentiment traders overprice stocks with high idiosyncratic volatility that contributes to lower future returns. Chi et al. [29] also examine the impact of investor sentiment on the relation between stock returns and volatility in the Chinese stock market by using mutual fund flows as a proxy for investor sentiment for different stocks. The study finds strong negative cross-sectional relation between idiosyncratic volatility and expected stock returns. One explanation for this relationship is that investor sentiment has immense influence on stock returns in the Chinese stock market and that, may be due to the presence of many high speculative individual investors in the Chinese stock market, investor sentiment largely influences the asset prices.
Data descriptive statistics
The sentiment data is downloaded from Jeffrey Wurgler’s website. The monthly sentiment covers the period from July 1965 to December 2007. Seven different measures of investor sentiment are considered namely, closed-end fund discount (CEFD), market turnover (TURN), the number of IPOs (NIPO), the average first-day returns on IPOs (RIPO), the number of new accounts opened (NO.A/C), consumer confidence index (CCI) and the sentiment index. The sentiment index is constructed using CEFD, TURN, NIPO and RIPO. The daily individual stock returns are obtained from the Data stream. The sample period of the study spans from 2004 to 2011 with a total of 416 week data.
Table 1 presents the summary statistics of monthly volatility measures, IVEW, IVVW and MVOL that are defined as equal-weighted and value-weighted idiosyncratic volatilities across individual firms and the market volatility, respectively. Panel A shows that the average IVEW is higher than the average IVVW. This suggests that smaller firms in China have higher idiosyncratic volatilities. This result is consistent with the findings in the US and other stock markets. The average equalweighted idiosyncratic volatility is the same as the market volatility. However, MVOL has a significantly higher coefficient of variation than both IVEW and IVVW indicating that MVOL is more variable than the other two. IVEW and IVVW have almost the same coefficient of variation, an indication that they are equally variable. In Panel B, the results show that IVEW, IVVW and MVOL are correlated, with MVOL more correlated with IVVW.
| Panel A: Summary Statistics of Idiosyncratic Volatility | ||||||
|---|---|---|---|---|---|---|
| Mean | Median | Stdev | CV | Max | Min | |
| IVEW | 0.0157 | 0.0153 | 0.0041 | 0.2611 | 0.0254 | 0.0072 |
| IVVW | 0.0154 | 0.0146 | 0.0046 | 0.2987 | 0.0277 | 0.0068 |
| MVOL | 0.0157 | 0.0138 | 0.0072 | 0.4586 | 0.0361 | 0.0064 |
| Panel B: Correlation Table | ||||||
| IVEW | IVVW | MVOL | ||||
| IVEW | 1.0000 | |||||
| IVVW | 0.6279 | 1.0000 | ||||
| MVOL | 0.6320 | 0.9636 | 1.0000 | |||
Table 1: Summary statistics.
Table 2 reports the summary statistics and the correlations for the various sentiment measures; closed-end fund discount (CEFD), market turnover (TURN), the number of IPOs (NIPO), the average first-day returns on IPOs (RIPO), the number of new accounts opened (NO.A/C), consumer confidence index (CCI) and the sentiment index. The sentiment index is constructed through CEFD, TURN, NIPO and RIPO. As is evident from Panel A, each of the sentiment measures is strongly correlated with the sentiment index. Also RIPO has a positive correlation with CEFD and TURN, and CEFD is associated with NIPO and RIPO. Thus, smaller closed-end fund discounts relate more to the number of IPOs and returns on IPOs. The correlation between these sentiment indicators suggests that there is some common component that is shared by these indicators. As a result, these sentiment indicators are appropriate in measuring investor sentiment. In Panel B, when CCI is added to the proxies in Panel A, the results show that, with the exception of CCI, the sentiment measures are all highly correlated with the sentiment index. CCI, on the other hand, is negative and has low correlation with other sentiment measures, and little in common with the sentiment index. This is an indication that CCI may be a weak proxy for investor sentiment in the Chinese stock markets. Consequently, CCI is replaced with NO. A/C in Panel C and the results show that all sentiment measures are highly correlated with the sentiment index and more sentiment measures are correlated with each other. Almost the same results are obtained in Panel D when both CCI and NO. A/C are included. Further, in Panels C and D, CEFD, in contrast to the results in Panels A and B, is linked to TURN and RIPO while TURN is positively correlated with NIPO, RIPO and NO.A/C. The correlation between the sentiment indicators is not perfect, however sentiment index strongly correlates with the sentiment indicators (except CCI) suggesting potential benefits from incorporating individual sentiment indicators into a common index to include more information.
| Panel A: CEFD, TURN, NIPO and RIPO (2001.12 to 2011.08) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Summary Statistics | Correlation with | Correlation Matrix | ||||||||||
| Variable | Loading | Mean | SD | Min | Max | Sentiment | CEFD | TURN | NIPO | RIPO | ||
| CEFD | 0.4160 | -16.0447 | 12.5012 | -33.2086 | 23.4192 | 0.5200 | 1.0000 | |||||
| TURNt-1 | 0.3307 | 30.8924 | 21.1845 | 4.9292 | 92.6518 | 0.5658 | 0.0598 | 1.0000 | ||||
| NIPO | 0.4473 | 10.2155 | 10.3005 | 0.0000 | 37.0000 | 0.4250 | 0.3582 | 0.2538 | 1.0000 | |||
| RIPO | 0.2011 | 74.3114 | 70.6880 | 0.0000 | 343.6353 | 0.8186 | 0.2131 | 0.1115 | -0.0001 | 1.0000 | ||
| Panel B: CEFD, TURN, NIPO, RIPO and CCI (2001.12 to 2011.08) | ||||||||||||
| Summary Statistics | Correlation with | Correlation Matrix | ||||||||||
| Variable | Loading | Mean | SD | Min | Max | Sentiment | CEFD | TURN | NIPO | RIPO | CCI | |
| CEFD | 0.4146 | -16.0447 | 12.5012 | -33.2086 | 23.4192 | 0.5265 | 1.0000 | |||||
| TURNt-1 | 0.3284 | 30.8924 | 21.1845 | 4.9292 | 92.6518 | 0.5728 | 0.0598 | 1.0000 | ||||
| NIPO | 0.4508 | 10.2155 | 10.3005 | 0.0000 | 37.0000 | 0.4370 | 0.3582 | 0.2538 | 1.0000 | |||
| RIPO | 0.1927 | 74.3114 | 70.6880 | 0.0000 | 343.6353 | 0.8086 | 0.2131 | 0.1115 | -0.0001 | 1.0000 | ||
| CCIt-1 | 0.0577 | -0.0100 | 1.6042 | -9.5749 | 7.7258 | -0.0231 | 0.0450 | -0.0269 | 0.1128 | -0.0547 | 1.0000 | |
| Panel C: CEFD, TURN, NIPO, RIPO and No.A/C (2004.01 to 2011.08) | ||||||||||||
| Summary Statistics | Correlation with | Correlation Matrix | ||||||||||
| Variable | Loading | Mean | SD | Min | Max | Sentiment | CEFD | TURN | NIPO | RIPO | No. A/C | |
| CEFD | 0.2132 | -17.9557 | 12.1864 | -33.2086 | 20.3835 | 0.2488 | 1.0000 | |||||
| TURNt-1 | 0.3778 | 36.1903 | 20.6141 | 8.0491 | 92.6518 | 0.6683 | 0.2772 | 1.0000 | ||||
| NIPO | 0.1930 | 11.3804 | 11.2366 | 0.0000 | 37.0000 | 0.2200 | 0.5034 | 0.1732 | 1.0000 | |||
| RIPO | 0.3403 | 64.7137 | 69.4607 | 0.0000 | 334.6403 | 0.9269 | 0.0547 | 0.3141 | 0.0692 | 1.0000 | ||
| No. A/Ct-1 | 0.4187 | 13.2990 | 17.5021 | 0.6890 | 89.2420 | 0.8314 | 0.0988 | 0.6320 | 0.1187 | 0.7202 | 1.0000 | |
| Panel D: CEFD, TURN, NIPO, RIPO and No.A/C and CCI (2004.01 to 2011.08) | ||||||||||||
| Summary Statistics | Correlation with | Correlation Matrix | ||||||||||
| Variable | Loading | Mean | SD | Min | Max | Sentiment | CEFD | TURN | NIPO | RIPO | No. A/C | CCI |
| CEFD | 0.2139 | -17.9557 | 12.1864 | -33.2086 | 20.3835 | 0.2495 | 1.0000 | |||||
| TURNt-1 | 0.3772 | 36.1903 | 20.6141 | 8.0491 | 92.6518 | 0.6686 | 0.2772 | 1.0000 | ||||
| NIPO | 0.1941 | 11.3804 | 11.2366 | 0.0000 | 37.0000 | 0.2209 | 0.5034 | 0.1732 | 1.0000 | |||
| RIPO | 0.3393 | 64.7137 | 69.4607 | 0.0000 | 334.6403 | 0.9266 | 0.0547 | 0.3141 | 0.0692 | 1.0000 | ||
| No. A/Ct-1 | 0.4183 | 13.2990 | 17.5021 | 0.6890 | 89.2420 | 0.8315 | 0.0988 | 0.6320 | 0.1187 | 0.7202 | 1.0000 | |
| CCIt-1 | 0.0258 | 0.0147 | 1.3598 | -3.2853 | 7.7258 | -0.0192 | 0.0528 | -0.0417 | 0.1222 | -0.0095 | 0.0599 | 1.0000 |
| Sentiment – Correlation (2002.01 – 2011.08) | ||||||||||||
| Sentiment A | Sentiment B | Sentiment C | Sentiment D | CCI | ||||||||
| Sentiment A | 1.0000 | |||||||||||
| Sentiment B | 0.9998 | 1.0000 | ||||||||||
| Sentiment C | 0.9397 | 0.9348 | 1.0000 | |||||||||
| Sentiment D | 0.9400 | 0.9351 | 1.0000 | 1.0000 | ||||||||
| CCI | 0.1911 | 0.1823 | 0.3350 | 0.3347 | 1.0000 | |||||||
| Sentiment – Correlation (2004.01 – 2011.08) | ||||||||||||
| Sentiment A | Sentiment B | Sentiment C | Sentiment D | CCI | ||||||||
| Sentiment A | 1.0000 | |||||||||||
| Sentiment B | 0.9999 | 1.0000 | ||||||||||
| Sentiment C | 0.9397 | 0.9348 | 1.0000 | |||||||||
| Sentiment D | 0.9400 | 0.9351 | 1.0000 | 1.0000 | ||||||||
| CCI | 0.1562 | 0.1464 | 0.3350 | 0.3347 | 1.0000 | |||||||
Table 2: Summary statistics and correlation of sentiment measures.
Further, Table 2 shows that, for both periods 2002.01 to 2011.08 and 2004.01 to 2011.08, the sentiments are highly correlated. Sentiments C and D have high correlation with CCI while the correlation between CCI and sentiments A and B is low during the period 2004.01 to 2011.08.
Methodology
The study estimates the cross-sectional (time-series) relation between idiosyncratic volatility and expected stock returns (expected market returns) by considering the role investor sentiment plays in these relations.
The study uses Fama-French (FF) 3-factor model to measure idiosyncratic volatility for an individual firm. The idiosyncratic volatility for stock i in month t, 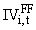 , is computed as
, is computed as
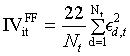
where 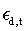 is estimated as a daily Fama-French 3-factor model in month t:
is estimated as a daily Fama-French 3-factor model in month t:
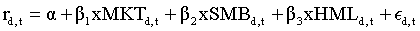
And rd,t is the daily return in month t, d is the day d in month t, Nt is the number of trading days in month t, and 22 is the number of trading days in one month.
In the case of investor’s sentiment, St represents the monthly sentiment at month t. The sentiment indicator Dt is given the value of one if St is greater than 0, and zero otherwise. The study’s regression treats sentiment as a continuous variable and as an indicator variable. In terms of aggregate idiosyncratic volatility, idiosyncratic volatility is computed as the average total variance across all individual stocks and the average of Fama-French 3-factor sum of squared residuals.
This section reports the empirical results. Table 3 presents the results of the relationship between idiosyncratic volatility (IV) and returns in the Chinese stock market over the sample period. It exhibits the average monthly raw returns and Carhart-4 alpha of stock portfolios sorted according to IV for equal-weighted portfolios and value-weighted portfolios. For both equal-weighted portfolios and value-weighted portfolios the high IV portfolios have lower raw returns and Carhart-4 alphas than low IV portfolios. The results indicate that the differences between high and low IV portfolios are all negative and statistically significant except for the value-weighted high IV portfolio for Carhart-4 alpha, which is almost statistically significant (alpha difference of -0.0052 with t-statistic of -1.6696). These findings are an indication that a negative idiosyncratic volatility effect is present in the Chinese stock market underpinning the Ang et al. [11] findings of negative idiosyncratic volatility puzzle.
| EW portfolios | VW portfolios | |||
|---|---|---|---|---|
| Raw return | Carhart-4 alpha | Raw return | Carhart-4 alpha | |
| High IV | -0.0057 (-0.5304) | -0.0101 (-3.8012) | -0.0064 (-0.6337) | -0.0047 (-2.0092) |
| Medium IV | 0.0057 (0.5413) | -0.0018 (-0.7621) | 0.0017 (0.1710) | 0.0027 (1.7673) |
| Low IV | 0.0075 (1.0272) | 0.0006 (0.3756) | 0.0042 (0.5149) | 0.0005 (0.2148) |
| High- Low | -0.0132 (-3.3344) | -0.0107 (-3.3536) | -0.0106 (-2.6693) | -0.0052 (-1.6696) |
Table 3: Returns on portfolios sorted by idiosyncratic volatility.
At the beginning of every month we sort stocks into three portfolios based on IV, i.e., High IV, Medium IV) and Low IV. We compute each portfolio’s equal- and value-weighted raw returns for the current month. We also estimate each portfolio’s alpha (α coefficient) from the FF3-factor model estimated using the full sample of monthly value- or equal-weighted returns for each portfolio. The last low of each panel presents the difference in monthly returns and differences in alpha between the high and low IV portfolios. T-statistics are reported in parenthesis.
Table 4 presents the various characteristics of portfolios sorted on idiosyncratic volatility with respect to Size, BM, Mom and REV (where Size at the end of month t is defined is the log of the firm’s market capitalization at the end of month t, BM is the firm’ book-to-market ratio of the portfolio in t-6, Mom is momentum at time t is the stock’s 11-month past return lagged one month, i.e. return from month t-12 to month t-2 and REV in month t is short-term reversal defined as the return on the stock in month t-1, following Lehmann [11]. The difference between the high IV and low IV portfolios is 0.0171with a t-statistic of 28.6095 and as such is highly significant. The difference in size is -1152.24 and is also statistically significant with a t-statistic of -3.0543 suggesting that the high IV portfolios mainly consist of big stocks. Momentum (Mom) is positive and exhibits little or no statistical significance indicating that high IV stocks do not show an intermediate-term momentum effect and hence momentum does not influence the IV effect. The difference in REV is 0.0422 with a t-statistic of 3.1049 suggesting that REV is positive and statistically significant. This indicates that recent winners turning into losers may explain the IV effect. The difference in BM is positive and statistically significant with a t-statistic of 2.5726 implying that BM may explain the IV effect.
| IV | Size | BM | Momentum | REV | |
|---|---|---|---|---|---|
| High IV | 0.0245 (48.8633) | 4574.93 (17.4675) | 0.3183 (32.2404) | 0.0532 (1.1749) | 0.0283 (2.3761) |
| Medium IV | 0.0152 (35.7716) | 5693.45 (17.4401) | 0.3505 (33.3935) | 0.0248 (0.5831) | -0.0045 (-0.4351) |
| Low IV | 0.0074 (41.6574) | 5727.17 (21.0937) | 0.2732 (18.8401) | -0.0227 (-0.7645) | -0.0139 (-2.1235) |
| High- Low | 0.0171 (28.6095) | -1152.24 (-3.0543) | 0.0451 (2.5726) | 0.0758 (1.4017) | 0.0422 (3.1049) |
Table 4 presents the various characteristics of portfolios sorted on idiosyncratic volatility with respect to size, BM, momentum and REV. The difference between the high IV and low IV portfolio is 0.0171with t-statistic of 28.6095 and as such is highly significant.
Table 4: Characteristics of portfolios sorted by idiosyncratic volatility.
At the beginning of every month we sort stocks into three portfolios based on IV, i.e., High IV, Medium IV and Low IV. Size at the end of month t is defined is the log of the firm’s market capitalization at the end of month t, BM is the firm’s book -to-market ratio six months prior, i.e. at the end of t-6. Following Fama [30] Mom, momentum, at time t is the stock’s 11-month past return lagged one month, i.e. return from month t-12 to month t-2. REV in month t is short-term reversal defined as the return on the stock in month t-1, following Lehmann [24]. The last row is the difference between the high and low IV portfolio. T-statistics are reported in parenthesis.
The main drawback of the above portfolio analysis is the loss of considerable information through aggregation; consequently firmlevel Fama-MacBeth cross-sectional regressions are used that are designed to check the reliability or robustness of the portfolio sort results reported previously.
Table 5 reports Fama and MacBeth [31] regression results. Panel A of Table 5 presents univariate regressions that show a significant negative IV effect inconsistent with the portfolio-level results. Thus, the idiosyncratic volatility is negatively and significantly related to expected returns in the Chinese stock market supporting the idiosyncratic volatility puzzle reported in Ang et al. [11] who report a negative IV effect in the US and international context. Thus, this finding implies that IV effect does matter in explaining cross-sectional stock returns in the Chinese stock market. This finding is surprising given that the Chinese stock market is dominated by individual or retail investors and the US stock market, on the other hand, is dominated by institutional investors. The negative IV effect in the Chinese stock market could be driven by retail investors who prefer high idiosyncratic volatility stocks and as such overpay for high volatility stocks [32-34]. This evidence suggests a risk-seeking behaviour among the Chinese investors. Size has a negative coefficient and is significant. This suggests that returns increase as size decreases. BM has a positive coefficient and is significant indicating that high BM stocks tend to have higher returns. MOM is negatively and insignificantly related to expected returns. The coefficient of REV is -0.0688 and is highly significant with a t-statistic of -4.24 indicating a negative short-term reversal effect that suggests that recent winners will be losers in the next period.
| Intercept | IV | SIZE | BM | MOM | REV |
|---|---|---|---|---|---|
| Panel A Univariate Analysis | |||||
| 0.0196 (2.37) | -0.7098 (-2.89) | ||||
| 0.0355 (2.14) | -0.0032 (-1.75) | ||||
| 0.0062 (0.53) | 0.0055 (2.29) | ||||
| 0.0095 (0.91) | -0.0045 (-0.72) | ||||
| 0.0076 (0.69) | -0.0688 (-4.24) | ||||
| Panel B Bivariate Analysis | |||||
| 0.0407 (2.73) | -0.6393 (-2.79) | -0.0027 (-1.58) | |||
| 0.0175 (2.09) | -0.7414 (-3.17) | 0.0067 (3.34) | |||
| 0.0199 (2.59) | -0.7269 (-3.18) | -0.0025 (-0.43) | |||
| 0.0164 (2.05) | -0.6747 (-2.73) | -0.0494 (-2.89) | |||
| Panel C Multivariate Analysis | |||||
| 0.0408 (3.37) | -0.6224 (-2.88) | -0.0034 (-2.51) | 0.0080 (4.77) | -0.0040 (-0.82) | -0.0505 (-3.26) |
Table 5: Univariate, bivariate and multivariate fama-macbeth regression results (2004.01–2011.08).
The results of the bivariate regressions with IV are presented in Panel B of Table 5. The findings reveal that the negative relation between idiosyncratic volatility and expected returns still remains highly significant which re-enforces the idiosyncratic volatility puzzle reported in Ang et al. [11]. The short-term reversal, REV remains statistically significant. Similarly, MOM is still negative and statistically insignificant and so is the SIZE. In Panel C of Table 5, the results of the multivariate regression are reported. The findings in Panel C clearly mimic the results of Panel A; the IV coefficient remains negative and highly significant. Consequently, firm-level cross-sectional regression results suggest an idiosyncratic volatility puzzle.
Each month from 2004:01 to 2011:08 we run a firm-level Fama- MacBeth cross-sectional regression of the return on that month with one-month lagged values of the control variables; the model as Ri,t+1=β0,t+β1,tIVi,t+β2,tSIZEi,t+β3,tBMi,t+β4,tREVi,t+β5,tMomi,t Each row reports the time-series averages of the slope coefficients and their associated t-statistics. IV is the standard deviation of the residuals of the FF3-factor model, using Fama [30] return lagged one month, i.e. returns from month t-12 to month t-2. REV in month t is shortterm reversal defined as the return on the stock in month t-1, following Lehmann [24]. Numbers in parentheses are t-statistics.
Table 6 reports the regression results after regressing the returns spread between high and low idiosyncratic volatility on four factors: market returns, SMB, HML, and WMD. The excess market return is the difference between the value-weighted market return and the risk free rate, SMB is the size factor defined as the excess return of small firms over big firms, HML is the value factor defined as the excess return of high book-to-market (BM) firms over low BM firms, and WMD (momentum) is the return difference between stocks winners and losers, because sentiment sensitive stocks are likely to be winners (losers) in periods of high (low) sentiment.
| Panel A Sentiment Index A | |||||||
| Panel A.a | |||||||
| rport3;t - rport1;t = a + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a | m | s | h | f | adjusted R2 | ||
| Equal-Weighted Return | -0.0107 | 0.3636 (13.0506) | -0.0379 (-0.4845) | -0.1425 (-1.4693) | -0.0862 (-1.2915) | 0.7062 | |
| (-4.3312) | |||||||
| Value-Weighted Return | -0.0051 | 0.2320 (5.2434) | -0.1473 (-1.1844) | -0.3959 | -0.0396 (-0.3742) | 0.2626 | |
| (-1.2903) | (-2.5708) | ||||||
| Panel A.b | |||||||
| rport3;t - rport1;t = a1*(1-Dt-1)+a2*Dt-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | a2 | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0085 (-2.4909) | -0.0127 (-3.9104) | 0.3676 (13.0376) | -0.0309 (-0.3932) | -0.1581 (-1.6064) | -0.0828 (-1.2386) | 0.7059 |
| Value-Weighted Return | -0.0048 (-0.8839) | -0.0053 (-1.0239) | 0.2324 (5.1708) | -0.1464 (-1.1673) | -0.3977 (-2.5346) | -0.0392 (-0.3682) | 0.2559 |
| Panel A.c | |||||||
| rport3;t - rport1;t = a+b*St-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a | b | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.007 (-1.9438) | -0.0002 (-1.4397) | 0.3642 (13.1346) | -0.0384 (-0.4927) | -0.1592 (-1.6375) | -0.0892 (-1.3423) | 0.709 |
| Value-Weighted Return | -0.0009 (-0.1585) | -0.0002 (-1.0017) | 0.2327 (5.2587) | -0.1478 (-1.1885) | -0.4144 (-2.6720) | -0.043 (-0.4054) | 0.2626 |
| Panel B Sentiment Index B | |||||||
| Panel B.a | |||||||
| rport3;t - rport1;t = a1*(1-Dt-1)+a2*Dt-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | a2 | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0086 | -0.0127 | 0.3680 (13.0088) | -0.0305 | -0.1581 (-1.6048) | -0.0831 | 0.7058 |
| (-2.5299) | (-3.8688) | (-0.3876) | (-1.2425) | ||||
| Value-Weighted Return | -0.0046 | -0.0055 | 0.2329 (5.1668) | -0.1456 | -0.3994 (-2.5431) | -0.0389 | 0.256 |
| (-0.8491) | (-1.0540) | (-1.1597) | (-0.3655) | ||||
| Panel B.b | |||||||
| rport3;t - rport1;t = a+b*St-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | b | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.007 | -0.0002 | 0.3643 (13.1377) | -0.0381 | -0.1595 (-1.6410) | -0.0891 | 0.7091 |
| (-1.9433) | (-1.4453) | (-0.4892) | (-1.3409) | ||||
| Value-Weighted Return | -0.0009 | -0.0002 | 0.2327 (5.2601) | -0.1474 | -0.4147 (-2.6731) | -0.0428 | 0.2625 |
| (-0.1619) | (-0.9989) | (-1.1859) | (-0.4042) | ||||
| Panel C Sentiment Index C (2004.01 - 2011.08) | |||||||
| Panel C.a | |||||||
| rport3;t - rport1;t = a + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a | m | s | h | f | adjusted R2 | ||
| Equal-Weighted Return | -0.0131 (-4.6200) | 0.3859 (12.4674) | 0.0158 (0.1886) | -0.0815 (-0.7491) | -0.0675 (-0.9750) | 0.7494 | |
| Value-Weighted Return | -0.0049 (-1.0257) | 0.2317 (4.4706) | -0.1445 (-1.0302) | -0.3094 (-1.6988) | -0.0220 (-0.1901) | 0.2678 | |
| Panel C.b | |||||||
| rport3;t - rport1;t = a1*(1-Dt-1)+a2*Dt-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | a2 | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0095 (-2.8131) | -0.019 (-4.5158) | 0.3955 (12.7901) | 0.0407 (0.4872) | -0.0913 (-0.8505) | -0.0603 (-0.8832) | 0.7566 |
| Value-Weighted Return | -0.0018 (-0.3204) | -0.0099 (-1.3811) | 0.2398 (4.5607) | -0.1235 (-0.8688) | -0.3176 (-1.7409) | -0.016 (-0.1378) | 0.2668 |
| Panel C.c | |||||||
| rport3;t - rport1;t = a+b*St-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | b | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0044 | -0.0002 | 0.3927 (13.2518) | 0.0186 (0.2325) | -0.1081 (-1.0380) | -0.0746 | 0.7716 |
| (-1.1407) | (-3.0763) | (-1.1277) | |||||
| Value-Weighted Return | 0.0051 (0.7564) | -0.0002 (-2.0559) | 0.2395 (4.6926) | -0.1413 (-1.0257) | -0.3401 (-1.8951) | -0.0302 (-0.2649) | 0.294 |
| Panel D Sentiment Index D (2004.01 - 2011.08) | |||||||
| Panel D.a | |||||||
| rport3;t - rport1;t = a1*(1-Dt-1)+a2*Dt-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | a2 | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0095 (-2.8131) | -0.019 (-4.5158) | 0.3955 (12.7901) | 0.0407 (0.4872) | -0.0913 (-0.8505) | -0.0603 (-0.8832) | 0.7566 |
| Value-Weighted Return | -0.0018 (-0.3204) | -0.0099 (-1.3811) | 0.2398 (4.5907) | -0.1235 (-0.8688) | -0.3176 (-1.7409) | -0.016 (-0.1378) | 0.2668 |
| Panel D.b | |||||||
| rport3;t - rport1;t = a+b*St-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | b | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0044 (-1.1403) | -0.0002 (-3.0770) | 0.3927 (13.2523) | 0.0186 (0.2327) | -0.1083 (-1.0392) | -0.0745 (-1.1275) | 0.7716 |
| Value-Weighted Return | 0.0051 (0.7571) | -0.0002 (-2.0569) | 0.2395 (4.6929) | -0.1413 (-1.0256) | -0.3402 (-1.8959) | -0.0302 (-0.2648) | 0.294 |
| Panel E Sentiment Index E (CCI) | |||||||
| Panel E.a | |||||||
| rport3;t - rport1;t = a1*(1-Dt-1)+a2*Dt-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | a2 | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0094 | -0.0116 | 0.3636 (13.0080) | -0.0385 | -0.1424 (-1.4635) | -0.0849 | 0.7042 |
| (-2.5700) | (-3.8061) | (-0.4899) | (-1.2665) | ||||
| Value-Weighted Return | -0.005 | -0.0051 | 0.2320 (5.2198) | -0.1473 | -0.3959 (-2.5592) | -0.0395 | 0.2559 |
| (-0.8537) | (-1.0628) | (-1.1793) | (-0.3712) | ||||
| Panel E.b | |||||||
| rport3;t - rport1;t = a+b*St-1 + m*MKTt + s*SMBt + h*HMLt + f*WMLt + ϵt | |||||||
| a1 | b | m | s | h | f | adjusted R2 | |
| Equal-Weighted Return | -0.0026 | -7.45E-05 | 0.3636 (12.9929) | -0.0385 | -0.1439 (-1.4688) | -0.0855 | 0.7036 |
| (-0.0435) | (-0.1354) | (-0.4892) | (-1.2724) | ||||
| Value-Weighted Return | 0.0091 (0.0952) | -0.0001 | 0.2320 (5.2205) | -0.1483 | -0.3984 (-2.5605) | -0.0385 | 0.256 |
| (-0.1786) | (-1.1856) | (-0.3606) | |||||
Table 6: Risk-adjusted returns on portfolios with sentiment index dummy.
Table 6 also introduces the sentiment both as a continuous variable and as an indicator variable. The Panels A.a and C.a of Table 6 do not include the sentiment variables. The results confirm the findings in Table 5 that support the conclusion of Ang et al. [11] after controlling for market returns, SMB, HML, and WMD. Panels A.b, B.a, C.b, D.a and E.a report the results of the regressions that include high sentiment and low sentiment as dummy variables without the intercept. For equalweighted returns, the results show that when the sentiment is low, the returns difference is negative and significant after controlling for market returns, SMB, HML, and WMD. Similarly, during high sentiment periods, the returns difference is also negative and significant. These results indicate that the relation between idiosyncratic volatility and returns significantly depends on investor sentiment during both low and high sentiment periods. This finding is consistent with the results of Chi et al. [29] who find that investor sentiment has an impact on the relation between stock return and idiosyncratic volatility in the Chinese stock market. In contrast, for value-weighted returns, the returns differences during low and high sentiment periods are insignificant suggesting that the trade-off between idiosyncratic volatility and returns does not rely on investor sentiment. Panel A.c, B.b, C.c, D.b and E.b reports the results when investor sentiment is considered as a continuous variable. The results are mixed. The results indicate that the negative idiosyncratic volatility puzzle does not depend on investor sentiment even after controlling for market returns, SMB, HML, and WMD in A.c, B.b and E.b. However, the findings in C.c and D.b confirm that the relation between idiosyncratic volatility and returns is negative and significantly depends on investor sentiment. Thus, higher investor sentiment leads to a lower idiosyncratic volatility-returns trade-off. The market returns are a significant explanatory variable in all the regressions. The value is also a significant explanatory variable in almost all the regressions.
Table 6 reports portfolio risk-adjusted returns for quintile portfolios sorted by idiosyncratic risk. In month t, we sort the stocks into 5 quintiles according to the lagged idiosyncratic risk. Quintile 1 (5) contains stocks with the lowest (highest) idiosyncratic risk. The sentiment data is downloaded from Jeffrey Wurgler’s website. St denotes investor sentiment at month t, and Dt-1 is 1 if the monthly sentiment index in month (t-1) is greater than its median and 0 otherwise. Panel A reports the regression results without the sentiment dummy variable, Panel B reports the regression results with the sentiment dummy included, and Panel C treats sentiment as a continuous variable. t-statistics are reported in parentheses below the coefficients. R-square is reported in the last column.
Table 7 reports the results of the investigation of portfolio returns (both equal- and value- weighted) during high and low sentiment periods. In Panel A of Table 7, for both low and high sentiment periods, the findings show that the returns differences are negative and significant for equal-weighted portfolios suggesting a strong negative relationship between the stocks’ idiosyncratic volatility and expected returns. This is consistent with Gao et al. [28] findings that investor sentiment plays an essential role in the puzzling relation between idiosyncratic volatility and expected stock returns. In addition, the findings show that there is no significant relationship between stocks’ idiosyncratic volatility and expected returns for value-weighted portfolios, a result consistent with those in Table 6.
| Panel A Raw returns sorted by idiosyncratic volatility and Sentiment | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equal-wieghted | Value-weighted | |||||||
| High IV | Medium IV | Low IV | High IV-Low IV | High IV | Medium IV | Low IV | High IV-Low IV | |
| High Sentiment | 0.0122 (0.5683) | 0.0277 (1.2796) | 0.0265 (1.8352) | -0.0143 (-1.7788) | 0.0054 (0.2516) | 0.0119 (0.5637) | 0.0172 (0.9686) | -0.0118 (-1.3311) |
| Low Sentiment | -0.0115 (-0.7040) | -0.0007 (-0.0464) | 0.0007 (0.0682) | -0.0122 (-1.9644) | -0.0106 (-0.7165) | -0.0021 (-0.1478) | -0.0035 (-0.3077) | -0.0071 (-1.2884) |
| High Sentiment – Low Sentiment | -0.0020 (-0.2010) | -0.0046 (-0.4441) | ||||||
| Panel B Portfolios sorted by idiosyncratic volatility and Sentiment and Carhart-4 alpha results | ||||||||
| Equal-wieghted | Value-weighted | |||||||
| High IV | Medium IV | Low IV | High IV-Low IV | High IV | Medium IV | Low IV | High IV-Low IV | |
| High Sentiment | -0.0169 (-2.9100) | -0.0057 (-1.0016) | 0.0030 (0.7287) | -0.0199 (-2.7789) | -0.0050 (-0.9938) | -0.0005 (-0.1225) | 0.0027 (0.5433) | -0.0077 (-1.0781) |
| Low Sentiment | -0.0062 (-1.6364) | 0.0013 (0.4311) | 0.0002 (0.0652) | -0.0064 (-1.4240) | -0.0006 (-0.1969) | 0.0058 (2.8999) | -0.0056 (-2.3982) | 0.0050 (1.2430) |
| High Sentiment – Low Sentiment | -0.0135 (-1.5968) | -0.0044 (-0.7345) | ||||||
Table 7: Raw returns and alphas sorted by idiosyncratic risk and sentiment.
In panel B of Table 7, during high sentiment periods, the alpha difference is negative and significant suggesting a strong negative relation between the stocks’ idiosyncratic volatility and expected returns. This clearly indicates the existence of a negative relation between volatility and subsequent returns during high sentiment periods. In contrast, in the low sentiment regime, the value-weighted alpha spread is not significant indicating that the relation between idiosyncratic volatility and subsequent returns is not present in the Chinese stock market when investor sentiment is low. This is consistent with Gao et al. [28] who find negative relation between idiosyncratic volatility and expected stock returns during high sentiment periods while there is no clear relationship during low sentiment periods. The reason may be attributed to the fact that, during high sentiment periods, stocks with high idiosyncratic volatility are overpriced by the optimistic traders leading to lower subsequent returns for these stocks and hence the relation between idiosyncratic volatility and expected stock returns is negative.
Table 8 reports the results of the high sentiment portfolio Carhart-4 alpha sort by idiosyncratic volatility and control variables. Panel A of Table 8 reports the results when we double-sort on size and IV. The results show that the average equal-weighted and value-weighted alpha differences for both SMA (Small size) and MED (Medium size), during high sentiment period, are negative and have significant impact on returns. Therefore, medium and small size stock portfolios could explain the negative idiosyncratic volatility effect. In contrast, during high sentiment period, alpha differences for the BIG are negative but insignificant. This implies that big size stock portfolios could not explain the idiosyncratic volatility effect. In Panel B, we double sort on BM and IV, and the results indicate that HBM, MBM and LBM are statistically significant during high sentiment period for equal-weighted portfolios. This suggests that HBM, MBM and LBM could explain the negative relation between idiosyncratic volatility and expected returns. However, for value-weighted portfolios only MBM has an effect on returns. In Panel C, we double sort on momentum and IV. For equalweighted portfolios the findings show that MID, WNR and LSR (momentum) are negative and have significant effect on returns during high sentiment period. In contrast, for value-weighted portfolios only MID has an effect on returns during high sentiment period. In Panel D, we double sort on REV and IV, and the findings reveal that REV is negative and has little or no effect on returns during high sentiment period suggesting an insignificant relation between idiosyncratic volatility and expected stock returns during high sentiment period.
| Panel A. Double sort on size (market capitalization) and IV | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equal-weighted | Value -weighted | |||||||
| LIV | MIV | HIV | HIV-LIV | LIV | MIV | HIV | HIV-LIV | |
| BIG | 0.0007 (0.1365) | -0.0008 (-0.1815) | -0.0104 (-2.0172) | -0.0111 (-1.5174) | 0.0020 (0.3463) | 0.0048 (0.9150) | -0.0037 (-0.6885) | -0.0057 (-0.7247) |
| MED | -0.0038 (-0.5761) | -0.0104 (-1.5646) | -0.0237 (-3.3116) | -0.0199 (-2.0316) | -0.0037 (-0.5401) | -0.0099 (-1.5577) | -0.0238 (-3.3334) | -0.0201 (-2.0398) |
| SMA | 0.0130 (3.5112) | -0.0057 (-0.8978) | -0.0178 (-2.8992) | -0.0307 (-4.2955) | 0.0144 (2.7197) | -0.0059 (-0.8790) | -0.0190 (-3.1634) | -0.0334 (-4.1714) |
| AVE | 0.0033 (1.0652) | -0.0056 (-1.6497) | -0.0173 (-4.8297) | -0.0206 (-4.3583) | 0.0042 (1.2295) | -0.0037 (-1.0372) | -0.0155 (-4.3116) | -0.0197 (-3.9608) |
| Panel B. Double sort on BM and IV | ||||||||
| HBM | 0.0004 (0.0772) | -0.0072 (-1.2880) | -0.0142 (-2.5787) | -0.0146 (-1.9748) | -0.0027 (-0.4249) | -0.0147 (-2.6440) | -0.0126 (-1.9420) | -0.0099 (-1.0903) |
| MBM | 0.0040 (0.6810) | -0.0056 (-0.8254) | -0.0173 (-2.6666) | -0.0213 (-2.4378) | 0.0139 (2.0511) | 0.0057 (0.7634) | -0.0051 (-0.7442) | -0.0190 (-1.9750) |
| LBM | 0.0058 (1.1961) | -0.0076 (-1.2851) | -0.0193 (-3.2521) | -0.0251 (-3.2712) | -0.0003 (-0.0467) | 0.0075 (1.4897) | -0.0070 (-1.1092) | -0.0067 (-0.7097) |
| AVE | 0.0034 (1.1237) | -0.0068 (-1.9263) | -0.0169 (-4.8955) | -0.0203 (-4.4262) | 0.0036 (0.9358) | -0.0005 (-0.1435) | -0.0082 (-2.1769) | -0.0118 (-2.1895) |
| Panel C. Double sort on momentum (11/1/1) and IV | ||||||||
| WNR | 0.0037 (0.7136) | -0.0047 (-0.9365) | -0.0164 (-2.7239) | -0.0202 (-2.5273) | 0.0060 (1.0861) | 0.0004 (0.0755) | -0.0040 (-0.6076) | -0.0100 (-1.1657) |
| MID | 0.0011 (0.1475) | -0.0058 (-0.9186) | -0.0191 (-2.9870) | -0.0202 (-2.0566) | 0.0045 (0.5603) | 0.0066 (0.6169) | -0.0143 (-1.9616) | -0.0188 (-1.7280) |
| LSR | 0.0102 (2.4760) | -0.0101 (-1.5319) | -0.0176 (-2.6241) | -0.0278 (-3.5331) | 0.0024 (0.4122) | -0.0063 (-0.7772) | -0.0084 (-1.2713) | -0.0108 (-1.2267) |
| AVE | 0.0050 (1.5067) | -0.0069 (-1.9777) | -0.0177 (-4.8053) | -0.0227 (-4.5753) | 0.0043 (1.1357) | 0.0002 (0.0481) | -0.0089 (-2.2573) | -0.0132 (-2.4125) |
| Panel D. Double sort on REV and IV | ||||||||
| WNR | -0.0157 (-1.5178) | -0.0199 (-2.9122) | -0.0299 (-4.6872) | -0.0142 (-1.1662) | ||||
| MID | 0.0077 (0.7497) | -0.0023 (-0.3692) | -0.0111 (-1.6062) | -0.0188 (-1.5186) | ||||
| LSR | 0.0015 (0.1242) | 0.0116 (1.6627) | -0.0005 (-0.0695) | -0.0019 (-0.1423) | ||||
| AVE | -0.0022 (-0.3490) | -0.0035 (-0.9118) | -0.0138 (-3.5775) | -0.0117 (-1.5839) | ||||
Table 8: High sentiment portfolio carhart-4 alpha by idiosyncratic volatility and control variables.
At the end of each month over the test period, stocks are doublesorted 3 × 3, first by the control factor (size, BM, momentum, and REV) into three portfolios and then within each portfolio we sort stocks again by idiosyncratic volatility measured using the local Fama-French three factor model (FF-3). The alpha of each value- and equal-weighted portfolio is presented with t-statistics in parentheses. To control for a particular factor, we average the alpha within each idiosyncratic volatility category ending up with three portfolios with dispersion in idiosyncratic volatility but containing all values of the factor being controlled. Size is the firm’s market capitalization at the end of month t; BM is the book-to-market ratio six months prior, i. e. at the end of t-6; momentum at time t is the stock’s 11-month past return lagged one month; REV is stock’s past month return. Low IV, Medium IV , High IV refer to low, medium, and high idiosyncratic volatility portfolio, respectively; BIG: big size; MED: medium size; SMA: small size; HBM, MBM , LBM: high, medium, low book-to-market, respectively; WNR; winner; MID: middle; LSR: loser.
Table 9 reports the results of the low sentiment portfolio Carhart-4 alpha sorted by idiosyncratic volatility and control variables. Panel A of Table 9 reports the results when we double-sort on size and IV. The results show that the value-weighted alpha difference for BIG during low sentiment period is positive and significant with a t-statistic of 1.8828. Therefore the big size stock portfolios explain the positive idiosyncratic volatility effect. In contrast, during low sentiment period, the value-weighted alpha differences for SMA are negative and significant with t-statistics of -3.0547 and -3.4217 for equal-weighted and value-weighted portfolios, respectively. This implies that small size stock portfolios could explain the negative idiosyncratic volatility effect. In Panel B, we double sort on BM and IV. The results indicate that only the large BM is statistically significant with a t-statistic of -1.7925 during low sentiment period. This suggests that only the large BM could explain the negative relation between idiosyncratic volatility and expected returns. In Panel C, we double sort on momentum and IV, and the results show that, for equal-weighted portfolios, WNR, MID and LSR are negative and have a significant effect on returns during low sentiment period. On the contrary, for value-weighted portfolios, only WNR and LSR could explain the negative relation between idiosyncratic volatility and expected returns. However, in Panel D, we double sort on REV and IV and none of the variables has a significant impact on returns suggesting that REV has an effect on returns during low sentiment period.
| Panel A. Double sort on size (market capitalization) and IV | ||||||||
|---|---|---|---|---|---|---|---|---|
| Equal-weighted | Value -weighted | |||||||
| LIV | MIV | HIV | HIV-LIV | LIV | MIV | HIV | HIV-LIV | |
| BIG | -0.0047 (-1.8569) | 0.0039 (1.4980) | 0.0007 (0.1976) | 0.0054 (1.2009) | -0.0049 (-1.8126) | 0.0072 (2.6821) | 0.0033 (0.9616) | 0.0082 (1.8828) |
| MED | -0.0019 (-0.5861) | -0.0027 (-0.6539) | -0.0095 (-2.0017) | -0.0076 (-1.3229) | -0.0022 (-0.6883) | -0.0026 (-0.6275) | -0.0096 (-1.9982) | -0.0073 (-1.2716) |
| SMA | 0.0050 (1.6578) | 0.0041 (1.2410) | -0.0091 (-2.6039) | -0.0141 (-3.0547) | 0.0054 (1.7652) | 0.0028 (0.8298) | -0.0108 (-2.9873) | -0.0161 (-3.4217) |
| AVE | -0.0005 (-0.3170) | 0.0018 (0.9091) | -0.0059 (-2.5518) | -0.0054 (-1.8753) | -0.0006 (-0.3438) | 0.0025 (1.2552) | -0.0057 (-2.4737) | -0.0051 (-1.7669) |
| Panel B. Double sort on BM and IV | ||||||||
| HBM | 0.0004 (0.1496) | -0.001 (-0.3662) | -0.0061 (-1.7291) | -0.0065 (-1.4834) | -0.0018 (-0.4807) | -0.004 (-1.3119) | -0.002 (-0.6537) | -0.0002 (-0.0476) |
| MBM | 0.0008 (0.2109) | 0.0024 (0.6442) | -0.0047 (-1.4446) | -0.0054 (-1.0004) | -0.0008 (-0.2284) | 0.0074 (2.7341) | 0.0003 (0.0553) | 0.0011 (0.1607) |
| LBM | -0.0004 (-0.1475) | 0.0031 (0.8889) | -0.0095 (-2.2597) | -0.009 (-1.7925) | -0.0097 (-1.9817) | 0.0069 (2.0735) | -0.0038 (-0.8071) | 0.0059 (0.8742) |
| AVE | 0.0002 (0.1387) | 0.0015 (0.7607) | -0.0068 (-2.9632) | -0.0070 (-2.4370) | -0.0041 (-1.7520) | 0.0034 (1.9530) | -0.0018 (-0.6663) | 0.0023 (0.6327) |
| Panel C. Double sort on momentum (11/1/1) and IV | ||||||||
| WNR | -0.0134 (-2.9210) | 0.0055 (1.3084) | 0.0018 (0.4035) | 0.0152 (2.3569) | -0.0159 (-2.4092) | 0.0088 (2.3378) | 0.0052 (1.0155) | 0.0211 (2.5281) |
| MID | 0.0076 (1.2754) | -0.0012 (-0.3496) | -0.0083 (-2.1964) | -0.0159 (-2.2512) | 0.0014 (0.2705) | 0.0013 (0.3334) | -0.0055 (-1.4025) | -0.0069 (-1.0560) |
| LSR | 0.0080 (1.9617) | -0.002 (-0.6392) | -0.0121 (-3.1997) | -0.0201 (-3.6147) | -0.0003 (-0.1062) | -0.0037 (-1.0575) | -0.0095 (-2.3775) | -0.0092 (-1.8865) |
| AVE | 0.0008 (0.2636) | 0.0008 (0.3694) | -0.0062 (-2.6458) | -0.0069 (-1.8805) | -0.0049 (-1.6646) | 0.0021 (0.9900) | -0.0033 (-1.3007) | 0.0016 (0.4238) |
| Panel D. Double sort on REV and IV | ||||||||
| WNR | -0.003 (-0.4546) | -0.0068 (-1.6835) | -0.0153 (-3.3084) | -0.0123 (-1.5338) | -0.0011 (-0.1727) | 0.0007 (0.1691) | -0.0082 (-1.7116) | -0.0071 (-0.8987) |
| MID | 0.0020 (0.2719) | 0.0007 (0.2083) | -0.0024 (-0.6557) | -0.0045 (-0.5333) | -0.0053 (-0.8269) | -0.0009 (-0.2564) | 0.0005 (0.0636) | 0.0057 (0.5997) |
| LSR | 0.0092 (2.1857) | 0.0026 (0.5169) | -0.0011 (-0.1408) | 0.0036 (0.4019) | -0.006 (-0.8066) | 0.0107 (2.4588) | 0.0017 (0.3263) | 0.0076 (0.8491) |
| AVE | 0.0028 (0.6609) | -0.0012 (-0.5053) | -0.0063 (-2.4390) | -0.009 (-1.8440) | -0.0041 (-1.0607) | 0.0035 (1.4893) | -0.002 (-0.6098) | 0.0021 (0.4074) |
Table 9: Low sentiment portfolio carhart-4 alpha by idiosyncratic volatility and control variables.
At the end of each month over the test period, stocks are doublesorted 3 × 3, first by the control factor (size, BM, momentum, and REV) into three portfolios and then within each portfolio we sort stocks again by idiosyncratic volatility measured using the local Fama-French three factor model (FF-3). The alpha of each value- and equal-weighted portfolio is presented with t-statistics in parentheses. To control for a particular factor, we average the alpha within each idiosyncratic volatility category ending up with three portfolios with dispersion in idiosyncratic volatility but containing all values of the factor being controlled. Size is the firm’s market capitalization at the end of month t; BM is the book-to-market ratio six months prior, i. e. at the end of t-6; momentum at time t is the stock’s 11-month past return lagged one month; REV is stock’s past month return. Low IV, Medium IV , High IV refer to low, medium, and high idiosyncratic volatility portfolio, respectively; BIG: big size; MED: medium size; SMA: small size; HBM, MBM , LBM: high, medium, low book-to-market, respectively; WNR; winner; MID: middle; LSR: loser.
Table 10 presents the results of the univariate, bivariate and multivariate Fama-Macbeth regressions during the high sentiment period between 2004.01 and 2011.08. In Panel A, the univariate regression results indicate the presence of a negative relation between idiosyncratic volatility and expected stock returns during high sentiment period. However, the bivariate regression results in Panel B show the negative idiosyncratic volatility effect but only after controlling for BM and MOM separately. On the contrary, in Panel C the multivariate regression results show no discernible relation between idiosyncratic volatility and expected stock returns during high sentiment period. Further, all the models in Table 10 suggest that expected returns increase as size increases.
| Intercept | IV | SIZE | BM | MOM | REV |
|---|---|---|---|---|---|
| Panel A Univariate Analysis | |||||
| 0.0369 (2.62) | -0.7081 (-1.81) | ||||
| 0.0765 (3.45) | -0.0062 (-2.09) | ||||
| 0.0242 (1.28) | 0.0024 (0.67) | ||||
| 0.0306 (1.73) | -0.0105 (-1.38) | ||||
| 0.0242 (1.35) | -0.0824 (-3.51) | ||||
| Panel B Bivariate Analysis | |||||
| 0.0770 (3.60) | -0.5595 (-1.58) | -0.0052 (-1.89) | |||
| 0.0366 (2.62) | -0.7689 (-2.11) | 0.0041 (1.46) | |||
| 0.0394 (2.92) | -0.6850 (-1.81) | -0.0057 (-0.80) | |||
| 0.0299 (2.13) | -0.4708 (-1.29) | -0.0630 (-2.94) | |||
| Panel C Multivariate Analysis | |||||
| 0.0693 (3.27) | -0.3645 (-1.19) | -0.0047 (-1.93) | 0.0078 (3.15) | -0.0081 (-1.30) | -0.0665 (-3.28) |
Table 10: Univariate, bivariate and multivariate fama-macbeth regression results in the high sentiment (2004.01–2011.08).
Each month from 2004:01 to 2011:08 we run a firm-level Fama- MacBeth cross-sectional regression of the return on that month with one-month lagged values of the control variables; the model as Ri,t+1=β0,t+β1,tIVi,t+β2,tSIZEi,t+β3,tBMi,t+β4,tREVi,t+β5,tMomi,t. Each row reports the time-series averages of the slope coefficients and their associated t-statistics. IV is the standard deviation of the residuals of the FF3-factor model, using daily data for the previous 22 trading days. SIZE at the end of month t is defined is the log of the firm’s market capitalization at the end of month t, BM is the firm’s book -tomarket ratio 6 months prior, i.e. at the end of t-6. Fama [30], Mom is the Momentum at time t is the stock’s 11-month past return lagged one month, i.e. returns from month t-12 to month t-2. REV in month t is short-term reversal defined as the return on the stock in month t-1, following Lehmann [24]. Numbers in parentheses are t-statistics.
Table 11 reports the results of univariate, bivariate and multivariate Fama-Macbeth regressions during the low sentiment period between 2004.01 and 2011.08. The results for the univariate, bivariate and multivariate regressions show evidence of a negative idiosyncratic volatility effect in the Chinese stock market when investor sentiment is low. The results prevail even after controlling for, size, momentum, value and short-term reversal. Thus, the negative relation between idiosyncratic volatility and expected returns still remains highly significant reinforcing the idiosyncratic volatility puzzle reported in Ang et al. [11] when investor sentiment is low. The results also indicate that BM is statistically significant in all the regressions suggesting that higher value tends to have higher returns.
| Intercept | IV | SIZE | BM | MOM | REV |
|---|---|---|---|---|---|
| Panel A Univariate Analysis | |||||
| 0.0086 (0.86) | -0.7109 (-2.23) | ||||
| 0.0091 (0.40) | -0.0013 (-0.57) | ||||
| -0.0054 (-0.37) | 0.0076 (2.34) | ||||
| -0.0042 (-0.33) | -0.0006 (-0.06) | ||||
| -0.0030 (-0.21) | -0.0600 (-2.72) | ||||
| Panel B Bivariate Analysis | |||||
| 0.0174 (0.88) | -0.6907 (-2.28) | -0.0011 (-0.50) | |||
| 0.0052 (0.51) | -0.7237 (-2.36) | 0.0084 (3.05) | |||
| 0.0074 (0.83) | -0.7539 (-2.62) | -0.0005 (-0.06) | |||
| 0.0078 (0.82) | -0.8057 (-2.42) | -0.0408 (-1.66) | |||
| Panel C Multivariate Analysis | |||||
| 0.0225 (1.60) | -0.7882 (-2.67) | -0.0026 (-1.62) | 0.0081 (3.59) | -0.0013 (-0.19) | -0.0402 (-1.84) |
Table 11: Univariate, bivariate and multivariate fama-macbeth regression results in the low sentiment (2004.01–2011.08).
Each month from 2004:01 to 2011:08 we run a firm-level Fama- MacBeth cross-sectional regression of the return on that month with one-month lagged values of the control variables; the model as Ri,t+1=β0,t+β1,tIVi,t+β2,tSIZEi,t+β3,tBMi,t+β4,tREVi,t+β5,tMomi,t.Each row reports the time-series averages of the slope coefficients and their associated t-statistics. IV is the standard deviation of the residuals of the FF3-factor model, using daily data for the previous 22 trading days. SIZE at the end of month t is defined is the log of the firm’s market capitalization at the end of month t, BM is the firm’s book -to-market ratio 6 months prior, i.e. at the end of t-6. Following Fama [30], MOM is the Momentum at time t is the stock’s 11-month past return lagged one month, i.e. returns from month t-12 to month t-2. REV in month t is short-term reversal defined as the return on the stock in month t-1, Following Lehmann [24]. Numbers in parentheses are t-statistics.
Table 12 reports the results from regressing future excess market returns on present sentiment index, idiosyncratic risk and their interaction. None of the models in Table 12 is statistically significant. Thus, the results indicate that investor sentiment and idiosyncratic risk do not have predictive power for excess market returns in the Chinese stock market. Similarly, the interaction between investor sentiment and idiosyncratic risk does not predict future excess market returns in the Chinese stock market.
| Panel A Equal-Weighted Excess Market Return | |||
|---|---|---|---|
| β1 | β2 | β3 | R2 |
| rt+1 = a + β1*St + β2*IVew;t + β3St*IVew;t + εt+1 | |||
| 0.0001 (0. 0585) | 8.2510 (1.4583) | -0.0185 (-0.1845) | 0.0438 |
| rt+1 = a + β1*St + β2*IVvw;t + β3St*IVvw;t + εt+1 | |||
| 0.0007 (0.3904) | 7.2640 (1.4392) | -0.0472 (-0.5506) | 0.0292 |
| rt+1 = a + β1*Dt + β2*IVew;t + β3Dt*IVew;t + εt+1 | |||
| -0.0006 (-0.0045) | 5.3663 (1.0723) | 0.7613 (0.1068) | 0.0418 |
| rt+1 = a + β1*Dt + β2*IVvw;t + β3Dt*IVvw;t + εt+1 | |||
| 0.0235 (0.2042) | 3.5218 (0.7281) | -0.5887 (-0.0896) | 0.0245 |
| Panel B. Value-Weighted Excess Market Return | |||
| rt+1 = a + β1*St + β2*IVew;t + β3St*IVew;t + εt+1 | |||
| -0.0015 (-0.7403) | 2.2163 (0.3921) | 0.0700 (0.7005) | 0.0278 |
| rt+1 = a + β1*St + β2*IVvw;t + β3St*IVvw;t + εt+1 | |||
| -0.0003 (-0.1503) | 2.5855 (0.5102) | 0.0098 (0.1142) | 0.0101 |
| rt+1 = a + β1*Dt + β2*IVew;t + β3Dt*IVew;t + εt+1 | |||
| -0.0988 (-0.7877) | 1.4245 (0.2856) | 6.0462 (0.8505) | 0.0301 |
| rt+1 = a + β1*Dt + β2*IVvw;t + β3Dt*IVvw;t + εt+1 | |||
| -0.0461 (-0.4022) | 0.4789 (0.0977) | 3.1422 (0.4800) | 0.0131 |
Table 12:Predictive ability of sentiment, idiosyncratic risk, and their interaction (2004.01–2011.08).
We regress future monthly market excess returns on present sentiment index, idiosyncratic risk and their interaction. Here, the idiosyncratic risk is measured against FF 3-factor model or just the total variance. Both equal-weighted and value-weighted idiosyncratic risks across individual stocks are used in the regressions. The sentiment index is used either as a continuous variable (St) or as an indicator variable (Dt) that equals one if it is above its median. The aggregate idiosyncratic risk measure IV Tvw is the value-weighted total variance across individual stocks. The aggregate idiosyncratic risk measure IV FFvw is the value-weighted total Carhart 4-factor S.D. residual across individual stocks. The subscript ew denotes the equal-weighted measures of aggregate idiosyncratic risk, while vw denotes valueweighted measures of aggregate idiosyncratic risk. The t-statistics are given in the parentheses.
Table 13 reports the results from regressing both equal-weighted and value-weighted market returns on investor sentiment (both as continuous variable and indicator variable), the equal-weighted or value-weighted idiosyncratic volatility, market volatility and the interaction between investor sentiment and idiosyncratic risk by incorporating market volatility into the models in Table 12. In panel A of Table 13, the results show that both equal-weighted and valueweighted idiosyncratic volatility are positive and statistically significant. This implies that idiosyncratic volatility positively predicts future excess market returns. This finding is consistent with classical asset pricing theory. The idiosyncratic volatility effect is significantly positive among the most under-priced stocks [35]. Thus, among underpriced stocks, the idiosyncratic volatility effect is positive as stocks with high idiosyncratic volatility are the most underpriced when investor sentiment is low. On the contrary, the investor sentiments, as well as, the interaction of idiosyncratic volatility and investor sentiment do not predict future excess market returns. None of the variables in the models in Panel B of Table 13 is statistically significant. This means that the investor sentiment, and the interactions between investor sentiment and idiosyncratic are statistically insignificant. This finding indicates that investor sentiment does not have predictive power for future excess market returns in the Chinese stock market. Similarly, market volatility has no influence on excess market returns in any model [36-38].
| Panel A Equal-Weighted Excess Market Return | ||||
|---|---|---|---|---|
| β1 | β2 | β3 | β4 | R2 |
| rt+1 = a + β1*St + β2*MVt + β3*IVew;t + β4St*IVew;t + εt+1 | ||||
| 0.0006 (0.2889) | -2.5599 (-1.2554) | 12.1020 (1.8850) | -0.0393 (-0.3887) | 0.0608 |
| rt+1 = a + β1*St + β2*MVt + β3*IVvw;t + β4St*IVvw;t + εt+1 | ||||
| 0.0010 (0.5846) | -2.1317 (-1.0309) | 10.2720 (1.7623) | -0.0647 (-0.7413) | 0.0409 |
| rt+1 = a + β1*Dt + β2*MVt + β3*IVew;t + β4Dt*IVew;t + εt+1 | ||||
| 0.0071 (0.0564) | -2.9090 (-1.4250) | 8.6789 (1.5803) | 0.7712 (0.1088) | 0.0636 |
| rt+1 = a + β1*Dt + β2*MVt + β3*IVvw;t + β4Dt*IVvw;t + εt+1 | ||||
| 0.0334 (0.2898) | -2.0227 (-0.9865) | 5.8403 (1.0762) | -0.9996 (-0.1518) | 0.0353 |
| Panel B. Value-Weighted Excess Market Return | ||||
| rt+1 = a + β1*St + β2*MVt + β3*IVew;t + β4St*IVew;t + εt+1 | ||||
| -0.0010 (-0.4827) | -2.7445 (-1.3491) | 6.3451 (0.9907) | 0.0477 (0.4727) | 0.0477 |
| rt+1 = a + β1*St + β2*MVt + β3*IVvw;t + β4St*IVvw;t + εt+1 | ||||
| 0.0001 (0.0702) | -2.3015 (-1.1136) | 5.8331 (1.0013) | -0.0092 (-0.1050) | 0.0241 |
| rt+1 = a + β1*Dt + β2*MVt +β3*IVew;t + β4Dt*IVew;t + εt+1 | ||||
| -0.0905 (-0.7266) | -3.1778 (-1.5654) | 5.0432 (0.9234) | 6.0570 (0.8590) | 0.0567 |
| rt+1 = a + β1*Dt + β2*MVt +β3*IVvw;t + β4Dt*IVvw;t + εt+1 | ||||
| -0.0347 (-0.3023) | -2.3060 (-1.1306) | 3.0538 (0.5657) | 2.6738 (0.4083) | 0.0274 |
Table 13: Predictive ability of sentiment, idiosyncratic risk, market variance and their interaction.
We regress future monthly excess market returns on present investor sentiment (both as continuous variable and indicator variable), idiosyncratic risk, market volatility and the interaction between investor sentiment and idiosyncratic risk. Here, the idiosyncratic risk is measured against Carhart 4-factor model of individual stocks. We only report results for value-weighted (IV Tvw, and IV FFvw idiosyncratic risk across individual stocks [39-43]. St is investor sentiment in month t. MVt is the market volatility at month [44, 45].
In this paper, we examine the idiosyncratic volatility puzzle and explore whether investor sentiment influences the relation between idiosyncratic volatility and expected stock returns in the Chinese stock market [46-48]. The portfolio sorted results show that idiosyncratic volatility is negatively associated with returns [49-51]. Similarly, the Fama-Macbeth regression results confirm that the idiosyncratic volatility is negatively and significantly related to expected returns in the Chinese stock market. This finding is surprising given that the Chinese stock market is dominated by individual or retail investors while the US stock market, on the other hand, is dominated by institutional investors.
We introduce investor sentiment by regressing risk-adjusted returns on portfolios with sentiment index dummy (high and low sentiment periods) and then analyse the relation between idiosyncratic volatility and expected stock returns. With the introduction of the sentiment dummy variable, the findings show that the returns differences are negative and significant for equal-weighted portfolios in both low and high sentiment periods. This suggests a strong negative relation between idiosyncratic volatility and expected returns. The introduction of sentiment index (as a continuous variable) also indicates that the returns differences are negative and significant for both equal-weighted and value-weighted portfolios suggesting a strong negative relationship between idiosyncratic volatility and expected returns. Thus, the relation between idiosyncratic volatility and returns depends on investor sentiment in the Chinese stock market.
However, multivariate Fama-Macbeth regressions indicate that, during high sentiment periods, the relation between idiosyncratic volatility and expected stock returns is negative and insignificant after controlling for market returns, size, book-to-market and momentum. This suggests no discernible relationship between idiosyncratic volatility and expected stock returns. However, during the low sentiment, the univariate, bivariate and multivariate Fama-Macbeth regression results reveal a negative and significant relationhip between idiosyncratic volatility and expected stock returns after controlling for market returns, size, book-to-market and momentum. This exhibits that the relation between idiosyncratic volatility and future returns is strongly influenced by investor sentiment.
The predictive ability of sentiment, idiosyncratic risk and their interaction is also tested and the results reveal that investor sentiment and idiosyncratic volatility and their interaction do not predict future market returns in the Chinese stock market. In contrast, by incorporating market volatility into the regression, the results indicate that idiosyncratic volatility is positive and statistically significant, and therefore predicts returns. However, the investor sentiment and the interactions between investor sentiment and idiosyncratic volatility remain insignificant. Overall, the results are mixed depending on the regression employed.