Clinical & Experimental Cardiology
Open Access
ISSN: 2155-9880
ISSN: 2155-9880
Research Article - (2014) Volume 5, Issue 11
Background: To explore the conditions most dangerous for the emergence of sustained Ventricular Tachycardia or Ventricular Fibrillation (VT/VF) a new computational model of ventricular myocardium including 2592 finite elements in three dimensions was created.
Methods: The fully three dimensional model of right and left ventricular muscle was used to simulate the spread of electrical activation and the resulting electrocardiogram. Localized zones of ischemic muscle tissue were characterized by reduced conduction velocity and reduced refractory period, and VT/VF was initiated by single ectopic beats. The simulated body surface Electrocardiogram (ECG) was also computed.
Results: In this system clinically realistic VT/VF is readily produced by single stimuli. Reduced conduction velocity and reduced effective refractory period in localized abnormal muscle predispose to VT/VF. Transition to chaos was abrupt. No one specific pattern of re-entry, spiral waves, or vortices could be identified that later decomposed into VT/VF. Instead, there was a wide variety of activation patterns leading to chaos, depending sensitively on initial conditions. Nonetheless, a clear border between stable vs. chaotic behavior was defined by a critical threshold impulse wavelength, the product of conduction velocity and refractory period, γ*, in local ischemic tissue. This threshold, separating stable and chaotic regimes, can be specified precisely as γ*=FV1/3 , where V is the local volume of diseased tissue and 0 γ F γ 1 is a shape factor, near 1 for compact volumes and progressively smaller for flattened volumes. When the impulse wavelength is ≤γ*, VT/VF happens. Typical values for γ* range from 1 to 3 cm. Such behavior is characteristic of classical chaotic systems.
Conclusions: The patterns of muscle activation leading to self-sustaining VT/VF observed in three dimensional diseased hearts are much more complex and variable than traditional re-entry in two dimensions. Instead a model of abrupt transition to chaos emerges from the application of first-principles cardiac electrophysiology, realistic ventricular anatomy, and the pathophysiology of ischemic cardiac muscle. This phenomenon may represent a higher order form of mathematical chaos than has been previously studied.
Keywords: Arrhythmia; Ischemia; Physiology; Sudden cardiac death; Tachycardia; VT/VF
In ventricular tachycardia or ventricular fibrillation (VT/VF, or simply VF for short) wavelets of electrical activation propagate, seemingly randomly, across the myocardium, leading to profound reduction or complete loss of pumping action. The present research explores the genesis of ventricular fibrillation using a relatively simple three dimensional mathematical model to provide insights that would be difficult to obtain by clinical or experimental studies. In computer modeling one can create a realistically shaped three dimensional syncytium of ventricular tissue to study in detail the differences between self-limited ectopic beats and self-sustaining VT/VF. Such studies can capture the essence of underlying pathophysiology and shine light on some risk factors that make VF more likely by sharpening understanding of its proximal causes.
Specifying the exact electrophysiological mechanisms leading to VT/VF remains an open problem that has problem fascinated generations of physiologists [1]. From the earliest days of computers this particular problem has seemed almost ideal for computational biology, and numerical models of many types abound [1-3]. Many are two dimensional sheets of interconnected cells in which waves of activation propagate [4-8]. Some are fully three dimensional and hint that ventricular instability may occur more readily in three dimensions than in two dimensions [9-14]. Extension of current knowledge by incorporating all the features of the many published models into a new three dimensional model would be a highly complex and conceivably less than enlightening task. It would be preferable to study living hearts for their validity. Perhaps a better way forward from a modeling perspective is to envision the simplest possible model that incorporates key features relevant to human pathophysiology. These include three dimensional muscle mass shaped like human sized cardiac ventricles, at least one localized area of viable but ischemic muscle tissue, and the initiation of VT/VF by premature beats rather than by continuous electrical stimulation or rapid pacing. This paper takes a fresh look at a very old and fascinating problem, especially in the setting of local areas of viable but ischemic tissue characteristic of coronary artery disease, with the aim of defining the particular anatomic and physiologic conditions that lead to lethal ventricular instability.
Of special interest to the author is the possibility of initiating selfsustaining VT/VF with a single ectopic beat in diseased hearts. The conditions allowing sudden cardiac death to develop from a single premature beat are arguably the most dangerous for the patient. Such initial conditions have been rarely studied, as shown by the sample of previously published experimental and numerical models in Table 1. Most previous work has involved either electrically induced VF in normal hearts produced by rapid pacing or the transition from relatively stable VT to more chaotic VF, beginning with pre-existing spiral waves established in the initial state [7,13].
| Author, year, Reference | Method of VF initiation/model |
|---|---|
| Fenton and Karma, 1998 [9] | Initial condition in all the simulations was an untwisted scroll wave with a straight filament obtained by stacking along the z-axis identical two-dimensional spiral waves, or identical two-dimensional broken plane waves |
| Garfinkel, et al. 1992 [30] | Ouabain plus or minus epinephrine in arterial perfusate in rabbit hearts |
| Garfinkel et al. 1997 [31] | Ventricular fibrillation was induced by a short burst of 60-Hz alternating current in dog hearts. |
| Garrey, 1914 [29] | Strong faradic shocks in dog hearts. Studied termination of electrically induced VF |
| Gray et al. 1995 [11] | Sustained fibrillation in isolated rabbit hearts |
| Karma, 1994 [8] | Spiral wave breakup after a single spiral wave was initiated from a broken plane wave initial condition in numerical models |
| Kimura et al. 1986 [20] | Runs of extrasystolic impulses induced by premature stimuli (S2) at 10 min of ischemia in perfused cat ventricles. |
| Kimura et al. 1990 [21] | Burst of ectopic activity in isolated cat ventricular myocytes that developed during washout after superfusion with test solution |
| Moe, 1964 [4] | Computer model of hexagonal atrial cells in a flat sheet, paced at 200 Hz to initiate arrhythmias |
| Panfilov, 1998 [13] | Breakup of pre-existing spiral waves in 1000 x 700 element 2D model or 120×120×120 element 3D model |
| Qu, 2006 [7] | Initial conditions of multiple spiral waves were used and randomly perturbed to give rise to nonsustained fibrillation with different durations in a numerical model. |
| Samie and Jalife, 2001 [2] | Transition from VT to VF (a review of many models) |
| Vaidya et al. 1999 [32] | Bipolar pacing at basic cycle lengths (BCLs) of 80 and 120 msec (12 and 8.33 Hz) in Langendorff-perfused mouse hearts |
| Weiss et al. 1999 [3] | Transition from VT to VF (a review of many models) |
| Winfree, 1998 [1] | Brief review of many different models and systems used to induce VF electrically for experimental purposes. |
| Witkowski et al. 1998 [27] | Sustained ventricular fibrillation lasting more than 10 minutes was induced with a single critically timed electrical pulse (S2), applied after a constant pacing train (of S1 pulses). |
| Xu and Guevara, 1998 [5] | Rapid pacing for induction of arrhythmias in a computational model of a 2D sheet with small square of regional "ischemia", mimicked as increased extra-cellular potassium ion concentration |
Table 1: Partial survey of modes of initiation of ventricular fibrillation in experimental and numerical models.
Accordingly, the following investigation was done in silico to explore and identify the conditions most dangerous for the genesis of VF/VT in sick, three dimensional hearts. The initial state of the ventricles was quiescent, representing early to mid-diastole, at which time a single ventricular stimulus was applied at time zero, which resulted in either self-limited or self-sustaining activation. That is, a single ventricular beat, a short run of ventricular beats, or self-sustaining VT/VF was produced. Body surface electrocardiograms were also simulated, as previously described, to better connect the theoretical models with clinical experience and provide face validation [15].
To study the genesis of VT/VF a computer-based mathematical model of the cardiac ventricles was created to describe the spread of electrical activation throughout the myocardium and the resulting electrocardiogram. In keeping with the thinking of many authorities, the simulations are done in a three dimensional model of the ventricular myocardium [1,3,6,8,10,13,14]. The model is implemented in Microsoft Visual Basic code within an Excel spreadsheet on an ordinary laptop computer. Computation times range from a few seconds to a few minutes.
Geometry
Mesh pattern: The profile of the left ventricular endocardium is modeled as a radially symmetrical, roughly bullet shaped surface, covered with three layers of cardiac muscle. The ventricular cavity and wall thickness can be sized arbitrarily to model any degree of hypertrophy or dilatation. The muscle layers are divided into 18 parallel slices perpendicular to the long axis of the left ventricle, and each of these is divided into 48 segments in the circumferential or “hoop” dimension. Each segment has three muscle layers-subendocardial, mesocardial, and subepicardial, making for 18×48×3=2592 total finite elements. For initial simulations the radial profile of the endocardial surface was defined by a parabolic curve fit to a hand-drawn tracing of a typical left ventriculogram in diastole, using the equation r=2+0.65 n – 0.15 n2, where for a normal sized heart r is the radius in centimeters at node number, n, in the axial dimension, measured from the base of the heart toward the apex. In alternative models of larger and smaller hearts the linear dimensions of the model, including internal radii and the axial slice separation, were multiplied by factors ranging from 0.5 to 2.0.
Left ventricular free wall: The left ventricular free wall includes all three muscle layers. The thickness of each of the three radial layers can be independently specified and was taken to be 0.4 cm for normal hearts (1.2 cm total left ventricular wall thickness) and 0.9 cm for hypertrophied hearts (2.7 cm total left ventricular wall thickness).
Right ventricular wall and septum: The right ventricular free wall is specified as a curved extension of the outer, sub-epicardial muscle layer, covering 45 percent of the circumference of the left ventricle from base to apex. In the standard model the radius of the right ventricular muscle wall smoothly varied from 1.0 to 1.4 times that of the left ventricular sub-epicardial layer (Figure 1). The thickness of the right ventricular free wall was one third that of the left ventricular free wall. The thicknesses of the two inner layers comprising the interventricular septum were increased by a factor of 3/2, so that the total septal thickness was approximately the same as that of the left ventricular free wall.
Activation sequence
Propagation: Activation of the muscle in each finite element occurs either by pacing at a specified location containing an “irritable focus”, which in a healthy heart would initiate an ordinary premature ventricular contraction, or by conduction from adjacent muscle at a direction-dependent conduction velocity (30 cm/sec in the axial and hoop dimensions, 22 cm/sec in the radial dimension). For simplicity, axial and circumferential or hoop velocities are assumed in the net to be equal, in keeping with the generally helical wrapping of muscle fibers in a living heart, as well as the generally modest effects of fiber orientation noted in prior work [6,16-18].
The activation sequence is described by a set of activation times, τm,i,j , for each finite element at radial position, m, circumferential position, i, and axial position, j, in the model. The center of each element is called a node. The heart is assumed to be quiescent for at least a brief instant prior to the initiating ectopic beat. Time zero indicates the onset of the initiating ectopic beat. Initially activation times, τm,i,j , for all finite elements are set to −(latency+ERP) the sum of the local effective refractory period (ERP) and the latency of the ectopic beat after the end of the previous action potential. At time zero a selected finite element is activated, simulating the birth of a new ectopic beat. All other segments are activated by cell to cell conduction, and the time, τm,i,j>0, represents the time of arrival of the activation wave front at node (m, i, j).
The algorithm for tracking propagation of the wave of activation through the myocardium is similar to that described previously [19]. In brief, let k be an indexed node, and let n be a neighboring node in either the axial, hoop, or radial direction. Let t be clock time, and let τn be the activation time of neighboring node, n. If node k is repolarized (not refractory) and if node n is active, and if t−τn equals the impulse travel time between nodes k and n at the local conduction velocity, then k is listed to become active with τk=t at the beginning of the next time step Δt=0.001 sec. In this way the arrival of the activation wave front can be mapped as it spreads across the myocardium in terms of arrival times, τm,i,j , for all nodes (m, i, j) in the model. In the computational algorithm all nodes (m, i, j) are evaluated for arrival of a depolarizing wave front during each short time step, Δt, to update a list of future active nodes. Then the updated list is used during the next time step. This feature prevents possible streaking artifacts within any time step.
Repolarization: At the end of each time step every active node is checked; if t−τ equals or exceeds the assigned refractory period for the node, then the node is reset to the inactive, non-refractory state.
Modeling of purkinje fibers: Unless otherwise specified, the rapidly conducting Purkinje fibers in the subendocardium were modeled en mass by increasing axial conduction velocity in the subendocardial layer by 10-fold to represent the action of major branches of the His Purkinje system and by increasing circumferential conduction velocity in the subendocardial layer by 3-fold, to represent action of side branches of the Purkinje fibers. In some models this feature was turned off allowing for uniform conduction in all radial layers in the axial and hoop directions.
Activation displays: To show three dimensional movies of ventricular activation, an x,y,z coordinate system was defined for the chest with its origin at the base of the heart, the x-axis pointing to the left axilla, the y-axis pointing toward the feet, and the z-axis pointing anteriorly toward the sternum. The three dimensional coordinates for selected nodes are computed and superimposed on the x-y plane of the model and refreshed at a specified frame rate to create a move display. Locations of the active and passive nodes are logged separately. To create a movie of the temporal progress of the wave front of activation, the active nodes for which t−τ<20 msec are displayed graphically in a frontal (x, y) projection each 10 msec of simulation time. Additional target plots of all active and passive nodes in each of the three layers (endo, meso, and epicardial) can be optionally created every 10 msec. Together the three target plots display the states of all finite elements in the model.
Simulation of the electrocardiogram
To simulate the signal in Lead II, the sum of dipole potentials at a point on the axis of the left ventricle 8 cm from its center, 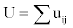 is computed from all pairs of nodes in the model representing boundaries in the axial or hoop dimensions between active and passive muscle, using the formula developed by Babbs,
is computed from all pairs of nodes in the model representing boundaries in the axial or hoop dimensions between active and passive muscle, using the formula developed by Babbs,
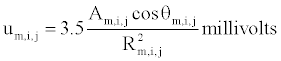 (1)
(1)
for area, Am,i,j, of propagating wave front between nodes in either the axial or hoop directions; angle, θm,i,j, between the axis of propagation and the line from the center of each dipole to the Lead II electrode; and distance, Rm,i,j, between the center of each dipole and the Lead II electrode. As excitation spreads outward from pacing sites around the myocardium, the summed electrical potential, U, traces a simulated wide QRS complex based upon the array of electrical dipoles created at the interfaces between depolarized (contracting) and polarized (resting) muscle tissue [15]. Since in this problem activation wave fronts tend to spread circumferentially and axially much more than radially (being initiated by a ventricular ectopic beat and not a conducted beat) the interfaces in the radial dimension were ignored for simplicity and speed of execution.
Parameter values
The standard model included 2592 nodes representing the left and right ventricular muscle. The base to apex distance was 9 cm. The maximal left ventricular radius was 2.7 cm. The thickness of left ventricular slices was 0.5 cm. Spread of the wave front of activation was computed every 0.001 sec. Wave front positions were tabulated every 0.01 sec.
Endocardial to epicardial gradients
Unless otherwise specified, gradients in conduction velocity and in refractory period ranging from endocardium to epicardium were established in keeping with published literature for normal and ischemic cardiac muscle [20]. The importance of such gradients in generating complex patterns of activation has been emphasized by Fenton [10]. Generally conduction is slower and refractory period is longer in subendocardial muscle compared to subepicardial muscle. The effect is attributed to relatively poor perfusion of subendocardial layers caused by high intracavitary pressures and greater effective distances from larger coronary arteries. This effect is exaggerated in ischemic muscle [21]. To mimic such gradients the normal subendocardial layer was assigned 10 percent longer than nominal refractory period when the gradient feature in the model was turned on, and subepicardial muscle was assigned 10 percent less than nominal refractory period. Similarly, the normal subendocardial layer was assigned 10 percent slower than nominal conduction velocity when the gradient feature in the model was turned on, and subepicardial muscle was assigned 10 percent faster than nominal conduction velocity. In abnormal, ischemic zones the corresponding gradients were increased from ±10 percent to ±33 percent.
Local ischemic tissue volumes
To model coronary artery disease a binary array IsAbnormal (m, i, j) is defined an anteroapical region of ventricular muscle having variably reduced impulse conduction velocity and/or variably reduced refractory period. The dimensions of this abnormal region, characteristic of the territory of the distal left anterior descending coronary artery, can be adjusted to create a large or small volume of local disease, simulating ischemic heart disease. The values of reduced refractory period and conduction velocity for each abnormal finite element are set as specified. Ischemic muscle physiology is simulated by adjusting the local abnormal conduction velocity between 0 and 100 percent of normal and the local refractory period between 50 and 100 percent of normal. Such changes in these physiologic parameters are characteristic of ischemic cardiac muscle [20,21]. The endocardial map of a typical local diseased region is presented in Figure 2.
Figure 2: Target plot of the endocardial layer showing abnormal vs. normal nodes. The subendocardial muscle layer is stretched so that all nodes are visible, anterior at bottom, posterior at top. The abnormal nodes correspond roughly to the distribution of the distal left anterior descending coronary artery. The isolated dot is the focus of the initiating ectopic beat.
Initiation of ectopic beats
To begin each simulation all nodes are assigned a quiescent state (repolarized) at time zero. Then one irritable focus is depolarized or set to the active state, initiating a premature ventricular beat, after which activation spreads outward by cell to cell conduction.
Self-limited conduction in a normal heart model
Figure 3 shows the simulated Lead II Electrocardiogram (ECG) and spatial activation patterns in a uniformly normal heart. A single Premature Ventricular Contraction (PVC) results in a onetime activation of the ventricular mass. Activation spreads outward from the site of origin. There is an orderly progression of the wave front of depolarization diagonally across the left ventricular muscle mass, after which the number of active nodes falls to zero. The sequence of depolarization is self-limited. The first positive wave of the ECG represents activation of ventricular muscle, or the QRS complex. The second positive wave represents subsequent repolarization of ventricular muscle, or the T wave. The T wave is large in part because repolarization is abrupt in this simplified model of electrophysiology. The total duration of the PVC is about 60 msec, similar to that in clinical recordings.
Self-propagating VT/VF in a diseased heart model
When an abnormal tissue volume corresponding to the distribution of the left anterior coronary artery is included, the results in Figure 4 are obtained. Here the abnormal region has slowed conduction velocity and shortened refractory period with an endocardial to epicardial gradient. The local refractory period is 0.5 times normal and the local conduction velocity is 0.3 times normal. A single stimulus produces sustained, selfpropagating activation of the ventricles. After 0.5 sec the ECG tracing shows a continual fibrillation like pattern, including high frequency components. The spatial pattern of activation of ventricular muscle becomes complex and chaotic. The average frequency of oscillations in the ECG is on the order of 10 Hz, as expected for ventricular fibrillation in human-sized hearts [22].
Figure 4: Simulated electrocardiogram (top) and spatial pattern of nodes activated in the previous 20 msec (bottom) in a model of local abnormal physiology. The absolute values are ERP 0.135 sec and conduction velocity 15 cm/sec in the abnormal, ischemic region. The ischemic region is denoted by dashed curves and arrows.
A plot of the percentage of nodes in Phase 0-1 of the action potential (0 to 20 msec from the instant of activation) as a function of time represents the composite volume of actively propagating wave front through the ventricular muscle mass. This wave front volume is illustrated by dots in the bottom two illustrations in Figure 4. As shown in Figure 5, in the case of self-limited PVC the wave front volume spontaneously falls to zero within one second (broken line). In the case of VT/VF the number of nodes comprising the active wave front of depolarization increases near the end of the first ectopic beat, indicating the breakout of a new wave fronts, and continues to rise and fall indefinitely.
Figure 5: Comparison of a self-limited PVC and one example of self-sustaining VT/VF in terms of the percentage of myocardium occupied by active wave fronts that are 0 to 20 msec old. PVC: refractory period 50% of normal, conduction velocity 60% of normal. VT/VF: refractory period 60% of normal, conduction velocity 30% of normal.
In such abnormal sustained ventricular rhythms the spatial patterns of activation are highly variable for various choices of locally reduced conduction velocity and refractory period. ECG patterns suggesting VT and those suggesting VF are not necessarily related to the corresponding differences in the degree of abnormality (Figure 6).
Irritable focus location
Interestingly, the emergence of VT/VF in this model does not depend strongly on the particular location of the irritable focus initiating ventricular excitation. That is, whether or not VF occurs does not depend on the origin of the triggering PVC, as would be expected on the basis of a classical re-entry paradigm [23]. The number of active nodes present at 1.0 sec for a near threshold abnormal physiology (velocity 30% of normal, ERP 60% of normal) for various initial activation sites ranged from 1493 to 2467. All stimulation sites produced VF. In no case was an isolated PVC observed. However, when a lesser degree of abnormality was tested (velocity 50% of normal, ERP 50% of normal) the number of active nodes at 1.0 sec for all sites tested was zero. That is, there was no VT/VF. This was not the result expected for a classical reentry mechanism is a two dimensional ring of tissue, in which pacing sites close to the edge of the abnormal area would be favored to induce “circus motion” and pacing sites diametrically opposite a uniformly abnormal area would produce a single beat [23] The expected re-entry like circus motion could be observed, as expected, only in degenerate models with one layer and one thin ring of tissue, but not in multilayered, three dimensional heart models.
Variations in model complexity
The essential self-sustaining nature of ventricular arrhythmias in this model does not depend on introduced complexities in the radial or wall thickness dimension. Similar arrhythmias happen with uniform muscle in the radial dimension. However, increasing model complexity does increase the frequency content of the simulated ECG waveform. With purknje fibers turned on and myocardial gradients turned off, a self-propagating rhythm develops that is suggestive of multifocal VT (Figure 7(a)). Successive addition of complex elements, including endo to epicardial gradient of ERP, an endo to epicardial gradient in conduction velocity in the abnormal region, as well as the effect of lumped purkinje fibers, increases the complexity and frequency content of the simulated ECG waveform (Figure 7).
Figure 7: Simulated ECG tracings for VT/VF in models of increasing complexity in the endocardial to epicardial dimension. (a) Purknje fibers on and myocardial gradients off. (b) Endo to epicardial gradient of ERP added. (c) Endo to epicardial gradient in conduction velocity in the abnormal region also added with endocardial velocity being faster. (d) Lumped Purkinje fibers added to create the standard model.
Spatial activation sequences
In three dimensions the pattern of activation in the standard model is complex and chaotic. No obvious macro-re-entrant patterns of activation were observed. Slight variations in dimensions or geometry of the ventricular muscle produced large variations in the spatial patterns of activation. Although the model is completely deterministic (no random variables are included) the pattern of activation appears quite unpredictable, similar to VT/VF s. Figure 8 shows target plot snapshots of the middle layer of myocardium at times ranging from 0.2 to 1.2 seconds after initiation of VT/VF by a single ectopic beat. The target plots show active (red) vs. inactive (blue) muscle in the middle layer of the myocardium at various times after the initiating PVC. At 200 msec normal muscle is completely activated, and a wave of depolarization has encroached part way into the abnormal area at the 5 o’clock position. At 400 msec recovery of normal muscle has begun. At 600 msec there is recovery of some abnormal muscle. At 800 msec a second wave of activation is occurring. Completely different patterns of activation were seen for the subendocardial and subepicardial muscle layers that were only loosely coupled in time and space to the mesocardial patterns. There is no clear evidence of a “re-entry” or “circus motion”. There were no obvious rotors or vortices present when the sequence was viewed as a movie. (Some authors have described three dimensional scroll waves in complex numerical models of cardiac excitation in normal hearts [13]. In these models of electrically induced VF the scroll waves ultimately break down into genuinely chaotic patterns. Perhaps the presence of a local abnormal tissue zone in the present models causes breakup of nascent scroll waves so quickly that they cannot be recognized.)
Critical impulse wavelength defining stable and unstable domains
Although it was not possible to demonstrate a consistent pattern of wave front propagation leading to VT/VF in three dimensions, it was possible to define a clear region of stability and a clear region of chaos in parameter space. Let φ indicate the fraction of normal conduction velocity and β indicate the fraction of normal refractory period. If one plots a graph of the relative reduction in impulse conduction velocity, φ, as a function of the relative reduction in refractive period, β, within the local volume of diseased muscle, then stable and unstable domains are defined by a curve describing the threshold or largest value of impulse conduction velocity, φ, leading to VT/VF at any particular level of refractory period, . Figure 9 shows the results of such a threshold finding experiment, which was conducted by gradually reducing local conduction velocity at a given local refractory period in the abnormal or ischemic tissue until VT/VF appeared.
Figure 9: Border in two dimensional parameter space between stable physiologic conditions, above the curve, and unstable physiologic conditions, below the curve. Here the parameters refer to conditions in the localized region of abnormal or ischemic tissue, namely the relative reduction in impulse conduction velocity on the vertical axis and relative reduction in refractory period on the horizontal axis. Data points come from numerical experiments. The smooth curve is a hyperbola that represents a constant product of the two variables or 0.21 (y=0.21/x). This curve represents a nearly 80 percent reduction in impulse wavelength in the abnormal region of muscle.
In Figure 9 the border of instability in φ-β space forms a perfect hyperbola of the form φβ=0.21, indicating the critical fractional reduction impulse wavelength, which leads to self-sustaining VT/VF. The impulse wavelength is defined in cardiac electrophysiology as the product of conduction velocity and refractory period. It indicates the span of the zone of depolarized muscle in an advancing wave front of depolarization. The normal value of impulse wavelength in working myocardial cells is about (30 cm/sec)*0.27 sec or 8.1 cm [16,24]. The critical impulse wavelength, λ*, is the product of the conduction velocity and the refractory period in abnormal tissue. In Figure 9 the critical value of λ* is 21 percent of the normal impulse wavelength or 1.7 cm. The value λ* represents a measure of the instability of a particular size, shape, and thickness of abnormal ventricular muscle. The greater λ*, the smaller the functional impairment required to produce VT/VF.
Critical impulse wavelength in various models: Interestingly, the critical impulse wavelength, λ*, is relatively insensitive to variations in model complexity or style, as defined by the presence or absence of Purkinje fiber action that speeds conduction in the subendocardial muscle layer, or by the presence or absence of endo-to epicardial gradients in conduction velocity and refractory period. Table 2 compares values of λ* in four styles of ventricular muscle model: Purkinje fibers only, gradients only, both, and neither. In each of the four models a hyperbolic relationship very similar to Figure 9 was obtained, with modest differences in the values of λ* (Figure 10 and Table 2).
| Purkinje | Gradient | Critical wavelength ratio | Critical wavelength absolute (cm) |
|---|---|---|---|
| on | off | 0.20 | 1.6 |
| on | on | 0.21 | 1.7 |
| off | on | 0.22 | 1.8 |
| off | off | 0.17 | 1.4 |
Table 2: Relative and absolute critical impulse wavelengths in four models.
Figure 10: Borders in parameter space between stable physiologic conditions, above, and unstable physiologic conditions, below, the data points for 4 different models with varying complexity in the radial dimension of muscle thickness. On-off denotes Purkinje fiber action with no endo-to-epicardial gradients. Off-on denotes no Purkinje fiber action with endo-to-epicardial gradients. On-on denotes both Purkinje fiber action and endo-to-epicardial gradients. Off-off denotes neither refinement.
Critical impulse wavelength and ventricular wall thickness: Although functional differences of myocytes in the radial dimension did not strongly influence conditions for ventricular instability, there was an interesting dependence of λ* upon total ventricular wall thickness. When LV-wall thickness is increased from a nominal 1.2 cm to 2.4 cm, representing left ventricular hypertrophy (here without gradients) λ* increases roughly in proportion to myocardial wall thickness. In turn, instability increases with ventricular hypertrophy. The simulated electrocardiogram with purkinje fibers on and left ventricular wall thickness of 2.7 cm in Figure 11 shows increased voltage and abundant high frequency components.
Figure 12 shows the relationship between relative λ* and wall thickness. When myocardial wall thickness increases, smaller reductions in refractory period or conduction velocity are needed to produce VT/VF. When myocardial wall thickness decreases, greater reductions in refractory period or conduction velocity are needed to produce VT/VF. In the limit, when wall thickness ratio is decreased to 0.0333, making an LV wall only 1 mm thick, the normalized value of * becomes 0.4*0.3=0.120, corresponding to an absolute critical impulse wavelength of 0.97 cm. These results in a model of localized ischemia correspond to the findings of Winfree, who pointed out that the thickness of the myocardium is an important factor for fibrillation in an otherwise normal heart [25]. Other investigators, as well, have previously demonstrated the importance of wall thickness in a number of model systems [9-11,13]. These findings suggest that phenomena in the third, radial dimension are not necessary for the genesis of VT/VF, but do substantially increase the likelihood of VT/VF. Such results hint that a simple re-entry model, drawn in two dimensions cannot provide a satisfactory description of VT/VF in all cases.
Dependence of critical impulse wavelength on the volume and shape of a diseased region
Empirical results: An intriguing idea that emerges at this juncture is that the critical impulse wavelength may depend upon to the physical dimensions of the abnormal tissue volume. To explore this idea in silico one may create a wide variety of shapes and sizes of abnormal, “ischemic” tissue and gradually reduce the impulse wavelength until VT/VF appears. (Since conduction velocity in the radial dimension was two-thirds of that in the axial and hoop dimensions, the average conduction velocity in the three dimensions was used to compute the critical impulse wavelength leading to VT/VF.) For smaller ischemic zones, in which the width and length were similar to the thickness of abnormal tissue, the critical impulse wavelength, λ*, approximated the geometric mean length, s, of one side of the ischemic zone, namely the cube root of the total abnormal tissue volume. This value, s=V1/3, can be termed the characteristic linear dimension. The overall average critical wavelength was 1.7 cm, and the overall average characteristic linear dimension, s, was 2.5 cm. This result was similar to that of Panfilov and Hogeweg, who found that the critical mass for fibrillation in a cube was about one wavelength (the size of one side) [14]. Interestingly, however, as the length and/or width of the island of ischemic tissue became larger relative to its thickness, the measured critical wavelength for VT/VF tended to become somewhat less than s by factors ranging from 0 to 50 percent (Figure 13). For flattened volumes that are more extensive in length and width than in height, the value of the critical impulse wavelength λ*, was reduced, in keeping with the importance of ventricular wall thickness. This observation led to the hypothesis that λ* is related to the cube root of the abnormal tissue volume, multiplied by a form factor that describes the degree of flattening. If the form factor can be properly characterized, then the critical impulse wavelength can be predicted simply from knowledge of the abnormal tissue dimensions, the abnormal impulse conduction velocity, and the abnormal refractory period.
Figure 13: Comparison of measured critical impulse wavelengths required for VT/VT and the characteristic linear dimensions of abnormal, ischemic tissue zones. Characteristic linear dimensions, s, are calculated as the cube roots of ischemic tissue volumes. The dashed line at 45 degrees is the line of equality (y = x). These data are uncorrected for flattening.
Derivation a form factor based on the surface to volume ratio: Suppose a rectangular box has dimensions h ≤ w ≤ l, with smallest dimension, h. The surface to volume ratio of the box is (2lw+2lh+2hw)/ (lhw). A reasonable flattening factor can be defined as the surface to volume ratio for the box divided by the surface to volume ratio for a cube of sides, h, or
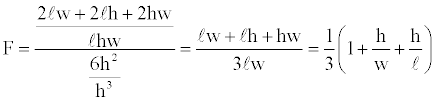 (2)
(2)
For a cube F=1. For progressively flatter volumes F approaches 1/3.
Prediction of the critical impulse wavelength: Using Equation (2) one can posit a formula to predict the critical impulse wavelength, λ*, based on the volume, V, and the dimensions, l, w, and h, of the abnormal tissue region as
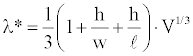 (3)
(3)
Equation (3) gives a simple rule describing the conditions for ventricular instability and sudden cardiac death in terms of fundamental anatomy and physiology. The fundamental anatomy is defined by the size and shape of the ischemic region. The fundamental physiology is defined by the critical impulse wavelength, which is the product of average conduction velocity and refractory period in the abnormal region. To test this idea the flattening factors were computed and multiplied by the characteristic lengths of ischemic tissue zones using Equation (3). Results are presented in Figure 14. The horizontal axis represents the measured threshold impulse wavelength for various abnormal heart models. The vertical axis represents the predicted threshold impulse wavelength.
Figure 14: Comparison of measured critical impulse wavelengths and values predicted using Equation (3), based on the physical dimensions of a single volume of abnormal, ischemic tissue. In the computational model the critical impulse wavelength, defining the abnormal physiology required for VT/VT, can be determined from the abnormal anatomy of the ischemic zone. The straight line at 45 degrees is the line of equality (y = x).
The empirical results for the model fall along the 45 degree line of equality, indicating that one can indeed predict the danger zone for ventricular instability from a first principles model, based upon fundamental anatomy and physiology.
The present study explores a three dimensional model of the right and left ventricular muscle mass, containing 2592 finite elements and including a zone of injured tissue to capture the essence of the mechanisms leading to VT/VF. Initiation of self-sustaining activation indeed occurs in response to a single ill-timed ectopic beat when there is a substantial volume of injured or compromised ventricular muscle tissue, having shortened refractory period, reduced conduction velocity, and overall reduced impulse wavelength to a critical level that is roughly 20 percent of normal. These abnormal conditions mimic the electrophysiological abnormalities of localized ischemia. The larger the absolute volume of depressed, abnormal tissue, the less is the critical reduction in impulse wavelength required for the emergence of VT/VF. The flatter and thinner the volume of depressed abnormal tissue, the greater is the critical reduction in impulse wavelength.
The dynamics of this type of lethal arrhythmia appear to show a very abrupt transition to a self-sustaining chaotic state. It was not possible to demonstrate a more orderly transition involving re-entry mechanisms or formation of vortices or scroll waves, unless the geometry of the model was reduced from three dimensions to a nearly two dimensional ring or thin slice of muscle tissue. Despite many days of searching, no repeated patterns suggesting simple re-entry were observed in fully three dimensional, human sized ventricular models. Further, the sites of origin of premature ventricular contractions (PVCs) leading to lethal VF were widely distributed and not necessarily concentrated in halo zones near islands of abnormal (i.e. ischemic) tissue. Instead, highly varied and chaotic patterns of sustained ventricular activation emerged suddenly under particular conditions, and the pattern of activation in time and space was sensitively dependent on the initial conditions (data not shown). All of these results are consistent with a model of abrupt transition to chaos.
Over the past 100 years a wide variety of thinkers have speculated about possible mechanisms for genesis of VT/VF or the transition from VT to VF, including factors such re-entry, spiral wave development and break up, oscillations in action potential duration causing conduction block, the presence of a high frequency stable source, drifting rotors, tissue in homogeneities both functional and anatomical, spatial gradients in refractory period, and a critical mass and shape of involved tissue [2]. Most of the forgoing mechanisms were demonstrated in initially normal tissue models without local disease (albeit with spatiotemporal variation in conduction velocity and excitability throughout the whole heart, as can happen with electrically induced VF). When discrete zones of localized ischemia are added to the mix, the number of actual dynamical mechanisms, i.e. explanations for specific patterns of wave front propagation in space and time leading to VT/VF, may be multiplied several fold. The result: a highly complex system in which the precise mechanism for initiation and maintenance of VT/VF in any particular case cannot be predicted. It is better, perhaps, to focus on clinically and physiologically important issues such as defining the critical conditions for initiation of VT/VF in patients with ischemic heart disease. In this regard a simple answer emerges from the present simulation study, namely that the size, shape, and impulse wavelength in the abnormal, rather than the normal, tissue volume set the stage for the initiation of VT/VF in response to an otherwise harmless premature ventricular beat.
The findings of the present study are by no means entirely new, and they recapitulate many themes in the past century of research in this intriguing field of inquiry. These themes include the importance of a critical mass of ventricular tissue, the importance of the wall thickness and shape of the critical mass, as well as the importance of the impulse conduction velocity and refractory period. Significant differences between two dimensional and three dimensional models are also well known from the literature. What is different from most prior work is the inclusion of discrete abnormal (ischemic) tissue volumes in the distribution of a particular coronary artery. Of course, real living hearts are likely to have inhomogeneous and dispersed areas of disease, whereas the present model has a single, homogenous area of disease. Although a single area of diseased tissue is a modest advance in sophistication over most models in this arena, future work could well include multiple abnormal zones having varying degrees of pathophysiology. Such localized disease has been rarely studied before, with two notable exceptions.
Previously Xu and Guevara described a two dimensional numerical model with simulated ischemia produced by increasing extracellular potassium concentration to 10 or 20 mM, causing partial or complete block [5]. The flat sheet had 1.25 cm square area. There was a 0.75×0.75 cm ischemic zone. Xu and Guevara found effects of wavelength and also anatomic scale. A second and especially interesting prior study that included abnormal tissue in three dimensions is that of Aliev and Panfilov [26]. This study describes simulation of wave propagation in the whole heart containing a local inhomogeneity mimicking cardiac tissue during an acute apical infarction. Short duration stimulation of the heart led to the development of a three dimensional vortex rings of active tissue lasting up to 819 msec after onset (their Figure 3). These findings at very early times are similar to those of the present study (see Figures 4 through 6). In the present study, however, the apparent vortices broke up to become chaotic shortly after 1000 msec. They were not stable and evolved toward greater complexity over periods of several seconds, as suggested by spiral wave breakup theories [8,9,13]. Whether the vortices of Aliev and Panfilov promptly devolved into chaos, as observed in the present study, was not reported, since simulations lasting more than 1000 msec were not described. Perhaps the authors were reluctant to challenge the prevailing vortex theory of the time by extending the simulations to longer times.
There is the distinct possibility that there are different types of VT/ VF having different electrical mechanisms, as pointed out by Witkowski, and coworkers [27]. These investigators studied the early phase of ventricular fibrillation produced by rapid ventricular pacing (S1, S1, S2 protocol, with S1-S1 at 238 msec) in normal perfused dog hearts. However, a “completely different electrophysiological pattern was seen when perfused ventricular fibrillation had persisted for 10 minutes. During ‘chronic’ ventricular fibrillation, no rotors were observed”. The geometry of activation became “more three dimensional”. This chronic form of VF without obvious rotors seems akin to the pathological form of VF described in the present study of three dimensional ventricular models with ischemia in the territory of the left anterior descending coronary artery. Perhaps chronic VF in normal hearts and ischemic VF in sick hearts are similar.
This possibility resonates with the theoretical idea that there are many routes to chaos mathematically. As pointed out by Harrison and Lai, the way that chaotic behavior develops as a system parameter changes depends upon the complexity of the underlying mathematics [28]. In low dimensional chaotic systems with only one positive Lyapunov exponent this transition often occurs via one of four known routes: the period-doubling cascade route, the intermittency transition route, the crisis route, and the route to chaos in quasiperiodically driven systems. However, transition to chaos in high-dimensional chaotic systems is more complex and less studied. Harrison and Lai studied one high dimensional system in which the transition happened in an abrupt fashion (see, for example, their Figure 4(b)). Perhaps VT/VF in three dimensional cardiac ventricles is an example of higher dimensional chaos. In this case, the abrupt transitions to chaos observed in the present study would not be mathematically unexpected.
Even in the relatively simple computational model presented here, the initiation of VT/VF in three dimensional diseased hearts is much more complex than the traditional explanations of re-entry and chaos would imply. The present study was begun with the expectation of finding clear patterns of re-entry, spiral waves, and rotors en route to VT/VF based on the idea first proposed by W.E. Garrey 100 years ago of “intramuscular ring like circuits with resulting ‘circus contractions’ which are fundamentally essential to the fibrillary process” [29]. However, when VF/VT is initiated from a resting state by a single ectopic beat in the presence of abnormal cardiac muscle in three dimensions, the expected circus contractions, spiral waves, and rotors, if present at all, were exceedingly fleeting (<1 sec). Instead, there was a sudden transition to a chaotic state.
Although specific dynamic patterns of electrical depolarization in time and space were not consistently observed during the initiation of VT/VF, the conditions for onset of lethal ventricular arrhythmias in a model of ischemic heart disease could be specified rather simply. The quantitative volume-shape formula proposed in the present work suggests that in this system the risk of VT/VF does not depend on the properties of the surrounding normal tissue but rather depends only on the volume, shape, and impulse wavelength of the ischemic zone.
Financial support: Purdue University internal funds.