Journal of Tumor Research
Open Access
ISSN: 2684-1258
ISSN: 2684-1258
Research Article - (2017) Volume 3, Issue 1
Using the entropy production rate method to determine the influence of glucose on a glycolysis model for HeLa tumor line, the greater complexity and robustness hypoglycemic phenotype was established. On the other side, inside the same metabolic phenotype a higher glucose concentration corresponds to a higher entropy production rate. It is concluded that this behavior is indicative of the directional character and stability of the dynamical behavior of cancer glycolysis.
Keywords: Cancer; Glycolysis; Entropy production rate; Glucose
Cancer is a generic name given to a complex interaction network of malignant cells that have lost their specialization and control over normal growth. This network could be modelled as a nonlinear dynamical system, self-organized in time and space, far from thermodynamic equilibrium, exhibiting high complexity, robustness, and adaptability [1]. Cancer cells, for the most part, show a high glycolytic rate and low pyruvate oxidation rate compared to normal cells, which brings with it a high consumption of glucose of the extracellular medium and an increase in the production of lactate, phenomenon known like “Warburg Effect” [2]. Increased glycolytic rate is beneficial for cell proliferation, as it provides the intermediates necessary for the synthesis of new nucleotides, lipids, amino acids and the generation of reducing power, all of which are necessary for cell division [3].The molecular mechanism behind the constitutive overexpression of aerobic glycolysis is not yet fully defined. Activation of oncogenes and tumor suppressor genes such as ras, c-myc, src and TP53 have implications for the regulation of aerobic glycolysis. These genes cause alterations in signalling pathways of growth factors and these in turn exert control over cellular metabolism [4]. Due to a combination of high glucose consumption rates by tumor cells and reduced tumor vascularization, the glucose concentration in the tumors can be 3 to 10 times lower than in normal tissues, according to the stage of its development. Therefore, tumor cells must develop strategies for their growth and survival in metabolically unfavorable environments [5]. Since the last years, cancer glycolysis has been a target in oncology research [6]. The significant increase of glycolysis rate observed in tumors has been recently verified, yet only a few oncologists or cancer researchers understand the full scope of Warburg’s work [6,7] despite of its great importance. Altered energy metabolism is proving to be as widespread in cancer cells as many of the other cancer-associated traits that have been accepted as hallmarks of cancer [8]. The regulation of metabolism, relevant to senescence process, would be a key to improve and identify new anti-cancer therapies in the future. The complex systems theory and the thermodynamics formalism in the last years have shown to be a theoretical framework as well as a useful tool to understand and forecast the evolution of the tumor growth [9-17]. The goal of this work is to extend the thermodynamics formalism previously developed [18-22] to the metabolic rate of human cancer cells. The manuscript is organized as follow: Firstly, a theoretical framework based on thermodynamics formalism, particularly the entropy production rate is presented. Then results and discussion are presented. Finally, some concluding remarks are presented.
Kinetic model of cancer glycolysis
The model used was proposed by Marin et al. [23] for the glycolytic network of HeLa tumor cell-lines growth under three metabolic states: Hypoglycemia (2.5 mM), Normoglycemia (5 mM) and Hyperglycemya (25 mM) during enough time to induce phenotypic change in cellular metabolisms. However, the growth saturation was not attained in this phase. In the other stage the cells were exposed to different glucose concentrations: 2.5 mM, 5 mM y 25 mM until they reach the stationary state. The rate of entropy production was calculated using the glycolysis network model of HeLa cell lines at steady state. The modelling of the metabolic network was made in the biochemical network simulator COPASI v 4.6 (Build 32) (http://www.copasi.org). The parameters and concentration values used were reported by Marin et al. [23].
Thermodynamics framework
As we know from classic thermodynamics, if the constraints of a system are the temperature T and the pressure P, then the entropy production can be evaluated using
Gibbs’s free energy [24], as:
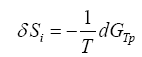 (1)
(1)
If the time derivative of (1) is taken, we have that:
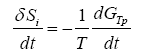 (2)
(2)
Where  represents the entropy production rate
represents the entropy production rate  The term
The term 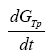 can be developed by means of the chain rule as a function of the degree of advance of the reaction ξ as:
can be developed by means of the chain rule as a function of the degree of advance of the reaction ξ as:
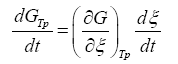 (3)
(3)
Where 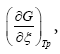 according to De Donder and Van Rysselberghe [25] represents the affinity Α with opposed sign and the term
according to De Donder and Van Rysselberghe [25] represents the affinity Α with opposed sign and the term 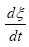 is the reaction rate ξ, this value was obtained from COPASI simulation for each one of the 22 reactions. The reaction rate ξcan be evaluated according to the difference between the forward ξf and backward reaction rates ξb
is the reaction rate ξ, this value was obtained from COPASI simulation for each one of the 22 reactions. The reaction rate ξcan be evaluated according to the difference between the forward ξf and backward reaction rates ξb
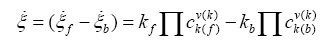 (4)
(4)
Taking into account (2) and (3), we get the entropy production rate in cells due to chemical processes driven by affinity as:
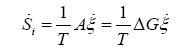 (5)
(5)
The variation of free energy of reaction (ΔGk) was calculated by the isotherm of reaction.
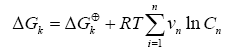 (6)
(6)
Where νn represent the stoichiometric coefficients, n C concentrations of the involved biomolecules in the stationary state and ΔGk⊕ the standard Gibbs free energy, which was adjusting for the physiological conditions: temperature T=310.15 K , ionic force I = 0.18 M and pH = 7 [26].
To calculate the rectified standard Gibbs free energy (ΔGk⊕) the equation (7) was used.
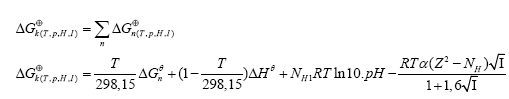 (7)
(7)
where: α is the Debye-Hückel constant 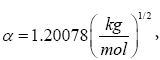 z is the specie charge, R is the universal gases constant 8.31 J/(mol.K) and H N is the average number of hydrogen atoms bond to the specie charge. R is the universal gases constant 8.31 J/(mol.K) and NH is the average number of hydrogen atoms bond to the specie. The fundamental postulate followed was: those reactions that exhibit a higher value of Si are considered fundamentals in the process [27,28]. This statement could be considered as extension of the ‘Principle of Maximum Entropy’ [29]. The entropy production rate was normalized in percent using as a baseline the highest value.
z is the specie charge, R is the universal gases constant 8.31 J/(mol.K) and H N is the average number of hydrogen atoms bond to the specie charge. R is the universal gases constant 8.31 J/(mol.K) and NH is the average number of hydrogen atoms bond to the specie. The fundamental postulate followed was: those reactions that exhibit a higher value of Si are considered fundamentals in the process [27,28]. This statement could be considered as extension of the ‘Principle of Maximum Entropy’ [29]. The entropy production rate was normalized in percent using as a baseline the highest value.
Substituting (6) and (4) on (5) is obtained:
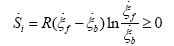 (8)
(8)
In a previous work [30] we have shown that the rate of entropy production is a Lyapunov function, in fact we extended this formalism to the development of cancer [31,32]. Thus we have the entropy production per unit time meets the necessary and sufficient conditions for Lyapunov function [33], therefore, it gives an evolutionary criterion and in addition, the global stability of the system.
We could write:
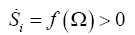 (9)
(9)
Where, Ω is the vector of control parameters. The Eulerian derivative (4.1) must meet:
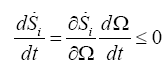 (10)
(10)
The Figure 1a shows the total entropy production rate ( Si ) obtained for HeLa tumor cellslines in three different metabolic phenotypes: hypoglycemia (2.5 mM), normoglycemia (5 mM) and hyperglycemia (25 mM). It is observed that the Si for the hypoglycemic phenotype (2.5 mM) is higher than the Si of others phenotypes, and the Si for the normoglycemic phenotype is higher than the Si of hyperglycemic phenotype. In addition, for the same metabolic phenotype, the cells exposed to higher extracellular glucose concentration (25 mM) showed the higher entropy production rate (see Figure 1b).
Finally, as shown in Table 1, for the transporters: GLUT and MCT1, and for the reactions catalyzed by the enzymes: HK, GADPH and PYK, the Si markedly changed when the cells transited from the extracellular glucose concentration of 2.5 mM to 25 mM in each metabolic phenotype. It is remarkable that when GLUT and HK are evaluated in 25 mM they turn out to be fundamental in the three metabolic phenotypes, in other words, exhibited a higher value of Si .
| Hypoglycemia | Normoglycemia | Hyperglycemia | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 2.5 mM | 5 mM | 25 mM | 2.5 mM | 5 mM | 25 mM | 2.5 mM | 5 mM | 25 mM | |
| Name/reaction | |||||||||
| GLUT Gluout = Gluin | 9 | 10 | 19 | 2 | 3 | 8 | 1 | 2 | 7 |
| HK Gluin + ATP = G6P + ADP | 13 | 15 | 27 | 4 | 7 | 19 | 3 | 5 | 16 |
| HPI G6P = F6P; Ery4P, FBP, 6PG | 6 | 6 | 7 | 4 | 5 | 6 | 5 | 5 | 6 |
| PFK1 F6P = FBP; ATP | 13 | 15 | 17 | 10 | 11 | 13 | 8 | 9 | 11 |
| ALDO FBP = DHAP + G3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| TPI DHAP = G3P | 9 | 11 | 13 | 7 | 7 | 9 | 6 | 7 | 8 |
| GAPDH NAD + G3P + Pi = 1,3BPG + NADH | 21 | 24 | 29 | 15 | 17 | 21 | 14 | 16 | 19 |
| PGK 1,3BPG + ADP = 3PG + ATP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PGAM 3PG = 2PG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ENO 2PG = PEP | 5 | 6 | 8 | 4 | 4 | 5 | 3 | 3 | 5 |
| PYK PEP + ADP = Pyr + ATP; FBP | 23 | 27 | 35 | 15 | 17 | 22 | 15 | 17 | 20 |
| LDH NADH + Pyr = Lac + NAD | 4 | 4 | 6 | 2 | 3 | 4 | 2 | 3 | 4 |
| GLYC DEG glycogen + Pi -> G6P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ATP asa ATP -> ADP + Pi | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| AK ATP + AMP = 2 * ADP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| DH asa NADH = NAD | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| PPP G6P -> 6PG | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| GLYC SYNT G6P + ATP -> glycogen + ADP + 2*Pi | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MPM Pyr + 13 * ADP + 13 * Pi -> 13 * ATP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| TK Xy5P + Ery4P -> G3P + F6P | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| MCT1 Lac in = Lac out | 22 | 25 | 31 | 17 | 20 | 26 | 16 | 18 | 23 |
| OxPhos ADP + Pi = ATP | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Metabolites: 1,3BPG: 1,3bisphosphoglycerate, 2PG: 2-phosphoglycerate, 3PG:3-phosphoglycerate,6PG: 6-phosphogluconate, DHAP: Dihydroxyacetone phosphate, Ery4P: Erythrose-4-phosphate, F2,6BP: fructose-2,6-bisphosphate, F6P: fructose-6- phosphate, FBP: fructose-1,6- bisphosphate,G3P: glyceraldehyde-3-phosphate, G6P: Glucose-6-phosphate, Gluint: Intracellular glucose, Gluout: Extracellular glucose, Lac: Lactate, PEP: Phosphoenolpyruvate, Pi: inorganic phosphate, Pyr: Pyruvate, Xy5P: Xilulose 5- phosphate. Enzymes: AK: Adenylate kinase, ALDO: Aldolase, ATPase: ATP-consuming processes, DHasa: NADH- consuming reactions, ENO: Enolase, GAPDH: Gliceraldehyde-3–phosphate dehydrogenase, GLUT 1y 3: Glucose transporters, HK: Hexokinase, HPI: Hexose phosphate isomerase, LDH: Lactate dehydrogenase, MPM: Mitochondrial pyruvate metabolism, PFK-1 – phosphofructokinase tipe 1, PGAM - 3- phosphoglycerate mutase, PGK - 3-phosphoglycerate kinase, PPP: pentose phosphate pathway, PYK: Pyruvate kinase, TK: Transketolase, TPI: triose phosphate isomerase. | |||||||||
Table 1: Entropy production rate (normalized values %) for glycolysis network model of HeLa tumor cells.
The highest values of entropy production rate were observed in the hypoglycemic phenotype, which means this phenotype exhibits higher robustness [20]. This can be correlated to the metabolic change induced in the HeLa cells lines grown in hypoglycemic conditions and its independence of the extracellular glucose conditions in the second face (2.5 mM, 5mM y 25 mM) until they reach the stationary state (Figure 1a). The sustained decrease of the glucose availability can stimulate changes in the cellular phenotype. For example KRAS mutations can increase the GLUT1 expression and that of many genes that codify the enzymes of the fundamental steps of glycolysis, likeHK1, HK2, PFK-1 and LDH-A, [33,34]. These changes imply an increase of glycolytic flow and consequently an increase of entropy production rate (Equation 5). Even if the extracellular glucose concentration returns to normal values, the changes can be maintained [35]. Moreover, the entropy production rate increases when exposed to higher extracellular glucose concentration in the three phenotypes (Figure 1b). Taking the glucose concentration like a control parameter and replacing in the equation (10), we have:
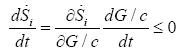 (11)
(11)
The glucose concentration decreases because is a reactant, thus we have dGlc dt<0; therefore, we must have 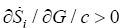 (Figure 1b). It is noted that the production of entropy per unit of time Si , evaluated through Equation (5) is indicative of the directional character and stability of the dynamical behavior of cancer glycolysis. One of the strategies used to fight the cancer has been the abrupt decrease of glucose concentration in the tumor microenvironment [6]. Cancer cells that develop accelerated glycolysis due to activation of oncogenes (including Ras, Her-2 and Akt) or due to loss of tumor suppressor function (including TCS1/2, p53, LKB1) undergo rapid apoptosis when placed in culture conditions with low glucose concentrations [6]. That is observed in Figure 1b for the three phenotypes. Therefore, glucose deprivation must be carried out in a shorter time than required by the tumor cells to acquire a characteristic phenotype. In this case the hypoglycemic phenotype which, as shown in Figure 1a, exhibits a higher entropy production rate, consequently will have a greater robustness. It´s known that the glucose deprivation markedly enhances oxidative stress by increasing the intracellular level of ROS [36]. ROS acts as a signal transduction messengers and can promote the proliferation or cellular death of cancer cells, depending of the intra and extracellular condition of the antioxidant defense mechanisms.
(Figure 1b). It is noted that the production of entropy per unit of time Si , evaluated through Equation (5) is indicative of the directional character and stability of the dynamical behavior of cancer glycolysis. One of the strategies used to fight the cancer has been the abrupt decrease of glucose concentration in the tumor microenvironment [6]. Cancer cells that develop accelerated glycolysis due to activation of oncogenes (including Ras, Her-2 and Akt) or due to loss of tumor suppressor function (including TCS1/2, p53, LKB1) undergo rapid apoptosis when placed in culture conditions with low glucose concentrations [6]. That is observed in Figure 1b for the three phenotypes. Therefore, glucose deprivation must be carried out in a shorter time than required by the tumor cells to acquire a characteristic phenotype. In this case the hypoglycemic phenotype which, as shown in Figure 1a, exhibits a higher entropy production rate, consequently will have a greater robustness. It´s known that the glucose deprivation markedly enhances oxidative stress by increasing the intracellular level of ROS [36]. ROS acts as a signal transduction messengers and can promote the proliferation or cellular death of cancer cells, depending of the intra and extracellular condition of the antioxidant defense mechanisms.
Cancer cells subjected to persistent endogenous and exogenous oxidative stress were shown to develop adaptive responses, mainly related to the upregulation and activation of the antioxidant machinery, which can contribute to cancer progression through an array of interconnected signals, amongst them, activation of RAS oncogene [37]. The bigger robustness of the hypoglycemic phenotype may be related to the increase of levels of ROS as consequence of low extracellular glucose concentration, and therefore is related to the contribution of ROS to the development and cell proliferation. The cells grown in hypoglycemic conditions could be adapted to a ROS-resistant phenotype, and this could be maintained even if the cells were later submitted to a high glucose concentration. In Table 1 is observed that the reactions that show a high Si variation in the range of 2.5 to 25 mM of glucose were GLUT, MCT1, HK, GADPH y PYK. This behaviour is related to the capacity of these proteins to change their flow in this range, in other words, an increase of their reaction rate and in consequence an increase of the entropy production rate (Equation 4).
The reactions GLUT and HK exhibit high values of Si for the glucose concentrations of 25 mM in the 3 phenotypes (Table 1); this behaviour was corroborated by the results of the studio of the sensibility analysis. Sensitivity analysis [38] quantitatively investigates the behavior of a system as a response to changes in parameter values. The transporter GLUT 1 performs a fundamental roll in many steps of cancer progression. It has been demonstrated that GLUT1 may regulate proteins that play a role in early tumor growth as well as in cancer invasiveness and metastasis [39]. Several studies demonstrate that hexokinase, particularly the Type II isoform (HK II), plays a critical role in initiating and maintaining the high glucose catabolic rates of rapidly growing tumors. Thus, it appears that hexokinase and its association with mitochondrial protein complex may play important roles in the essential homeostatic processes such as glucose metabolism and apoptosis. The inhibition of HK has significant effects in the metabolism and cell survival [40].
Using thermodynamics formalism of irreversible processes, complex systems theory and systems biology we propose and quantify a marker able to establish, in a quantitative way, the degree of malignancy of a human tumor cell. For this, it is used the fact that altered energy metabolism is proving to be as widespread in cancer cells as many of the other cancer-associated traits that have been accepted as hallmarks of cancer [8]. Thus, we propose that the regulation of metabolism, relevant to senescence process, would be a key to improve and identify new anti-cancer therapies in the future. In summary, in this paper we have found that:
1- Independently of the phenotype, it is shown how the increase of glucose concentration conduces to an increase of the total entropy production rate, which is indicative of the directional character and stability of the dynamical behaviour of cancer glycolysis.
2- The total entropy production rate that is shown by cancer glycolysis in the hypoglycemic phenotype is greater than those of the others states. In fact, this metabolic condition exhibits more robustness.
3- Any therapy directed to deplete a tumor from glucose, has to be completed in less time than that required by tumor cells to develop the hypoglycemic phenotype. The present theoretical framework will hopefully provide a better understanding of cancer and contribute to improvements in cancer treatment.
Extend this study to other tumor cell lines.
Prof. Dr. A. Alzola in memoriam. We would like to thank Prof. Dr. Jacques Rieumont for support and encouragement for this research. One of the authors (JMNV) thanked the Institute of Physics of the UNAM Mexico for its warm hospitality.