Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2014) Volume 3, Issue 4
In this paper, we investigate the importance of financial shocks for the Canadian business cycle employing the financial friction DSGE framework following Bernanke, Gertler, and Gilchrist with an extension of a small-open economy feature. In particular, we explored the importance of an external finance premium shock and an aggregate net worth shock. In order to identify financial shocks in the model, we utilized financial data in estimating our model. Our variance decomposition results showed that the external finance premium shock to account about 7.5% and the aggregate net worth shock to account about 5.6% of the variance of the business fixed investment in Canada. Also, our historical decomposition results and smoothing of the various financial variables showed that data on corporate leverage ratio to be particularly useful in identifying the financial shocks in the model. Finally, when the financial shocks were present in the model, relative importance of the investment-specific technology shock was substantially subdued that it accounted for only 17% of the variance of the business fixed investment –much lower than the results reported in the former empirical studies.
<Given the on-going financial crisis precipitated by the sub-prime loan problem in the U.S. financial sector, there has been an increased interest in the linkage between financial activity and real economic activity. In particular, there is a heightened interest in how the shocks occurring in the direct and/or indirect financial market can affect real economic activity. Although the Canadian banking sector seems to be weathering the current financial crisis [1] and have not experienced a major financial turmoil in recent decades1, there is no guarantee that the Canadian economy will be free from a large shock in the financial sector in a near future. In order to help the policy makers to understand the consequences of such contingency and to facilitate them in forming a counter-measure, it is crucial to assess how vulnerable (or robust) the Canadian economy is to the shocks originating in the financial sector. As such, we ask the following question in this paper; how important are financial shocks for the Canadian business cycle?
To answer the above question, we need to decide how to model the financial friction and financial shocks. In modeling the financial friction in a general equilibrium setting, there are mainly two approaches. One way is to impose collateral constraint as in Kiyotaki and Moore [2]. This collateral constraint approach is becoming a popular choice2, especially when modelling the financial friction in a mortgage loan market where residential asset is customarily withheld as collateral until the mortgage loan is repaid in full. Another approach is to model an external finance premium as in Bernanke and Gertler [3], Carlstrom and Fuerst [4], and Bernanke, Gertler, and Gilchrist [5]. This approach proved extremely useful3 in modelling the standard debt contract between the corporate sector and financial intermediary which allows us to analyze the relationship between business fixed investment and external financing cost. Both types of financial friction –collateral constraint and external finance premium –are useful in addressing the linkage between the financial market and real economic activity such as financial acceleration mechanism in residential investment and business fixed investment. However, since we are more interested in the fluctuation of the business fixed investment –the most important factor in output fluctuation –, we will be adopting the external finance premium as the financial friction mechanism in this paper. In particular, we construct a medium-scale dynamic stochastic general equilibrium (denoted DSGE, hereafter) model with financial friction à la Bernanke, Gertler, and Gilchrist [5] (denoted BGG, hereafter). Further, reflecting the Canadian context, we extend the model to incorporate a small-open economy feature.
Next, we need to decide the specifications of the financial shocks. In addition to the standard macroeco-nomic shocks adopted in the empirical DSGE literature, we adopt two types of financial shocks: external finance premium shock and corporate net worth shock. The importance of the external finance premium shock has been pointed out by Smets and Wouters [6,7]4, while the importance of the corporate net worth shock has been emphasized by Christiano, Motto, and Rostagno [8] (denoted CMR, hereafter). In the context of this paper, the external finance premium shock is an exogenous shock that affects the external finance premium (or credit spread) irrespective of corporate leverage ratio and can be interpreted as any shock affecting the credit spread without initially affecting the corporate balance sheet, such as financial market condition or financial intermediary’s lending attitude. The corporate net worth shock, in our context, is an exogenous shock to turn-over rate of entrepreneurs which, in turn, affects the credit spread through the aggregate leverage ratio of the corporate sector. Following CMR, this shock can be interpreted as an aggregate shock to the entrepreneurial net worth in the economy. Considering the importance of both types of financial shock as in Smets and Wouters [6,7] and CMR, we embed both of them to our benchmark model and compare which type of shock, external finance premium shock or corporate net worth shock, are relatively important in accounting for the Canadian business cycle.
As for the estimation of the model, we adopt the Bayesian estimation methodology which is becoming a standard tool in the empirical DSGE literature. Now, an issue remains. When there are two types of financial shock in the model and both shocks affect the non-financial variables via an external finance premium –the only channel that links non-financial variables and financial variables in BGG-type model –, inevitably, the qualitative pattern of the impulse response functions under both types of financial shock become similar, especially for the non-financial endogenous variables. Consequently, if the observable data in the estimation are confined to non-financial variables, we will face a difficulty in identifying the two financial shocks. In order to avoid this identification problem of the two financial shocks, we include financial variables (i.e., leverage ratio) to our observable data set, in addition to the standard non-financial data adopted in the empirical DSGE literature. Since the impulse response functions under the two financial shocks imply qualitatively different patterns for these financial variables, we claim that inclusion of financial variables to observed data will ensure the identification of two financial shocks in the estimation.
The main empirical findings of this paper can be summarized as follows. Under the shock specification where both financial shocks –external finance premium shock and aggregate net worth shock – are present in the model, it turns out that both financial shocks are quite important in accounting for the Canadian business cycle. Taking the case of business fixed investment in Canada, our variance decomposition for unconditional forecast error show that the external finance premium shock to account for as much as 7.5% and the aggregate net worth shock to account for as much as 5.6% of the variance. In total, the financial shocks account for more than 13% of the variance of the business fixed investment and this magnitude is comparable to that of an investment-specific technology shock. Based on this result, it will not be an over-statement to say that the financial shocks are as important as the investment-specific technology shock in accounting for the movement in the business fixed investment in Canada.
The remainder of this paper is organized as follows. Section 2 describes the model structure and the shock structure adopted in this paper. Section 3 explains the estimation strategies and also describes the data adopted in this paper. Section 4 reports the estimation results under four different shock specifications of the financial shocks. In particular, the posterior means of the parameters, estimated IRF, variance decompositions and historical decompositions will be reported. Section 5 explores the consequences of using alternative data set. In particular, this section demonstrates the importance of utilization of the financial data, especially leverage ratio data, in identifying the financial shocks. Section 6 summarizes and concludes the paper.
We basically adopt BGG as the workhorse in modelling financial frictions in the economy and extend it to incorporate the small open economy features –a necessary extension when analyzing the Canadian business cycle. The economy is populated by households consuming final goods and supplying labour inputs, entrepreneurs producing domestic intermediate goods, capital producers, monopolistically competitive wholesalers of domestic intermediate goods and imported goods, perfectly competitive retailers of final goods, a government and a monetary authority. The factor markets (capital market and labour market) are perfectly competitive. There are four types of rigidities in the economy: nominal price rigidity for wholesalers, external habit formation of consumption for households, investment adjustment costs for capital producers, and external finance premiums for entrepreneurs when borrowing credits. In this section, we describe the problem settings and the equilibrium conditions for each agent in turn.
Household’s problem
The representative household derives utility from final goods consumption and disutility from supplying labour inputs. The household strives to maximize their utility over time and their expected discounted sum of period-by-period utility function is specified as follows,
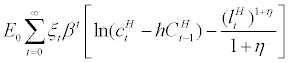 (1)
(1)
where parameter β stands for the discount rate by the household, 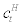 stands for final goods consumption, parameter h stands for habit persistence coefficient, and
stands for final goods consumption, parameter h stands for habit persistence coefficient, and 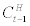 represents external habit formation which is exogenously given to the household at period t, but
represents external habit formation which is exogenously given to the household at period t, but 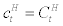 in equilibrium. Turning to the labour supply side of the utility function,
in equilibrium. Turning to the labour supply side of the utility function, 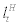 stands for the supply of labour inputs by the household, and parameter η stands for labour supply elasticity. Now,
stands for the supply of labour inputs by the household, and parameter η stands for labour supply elasticity. Now, 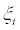 represents an intertemporal preference shock to the household’s current and future consumption and labour supply and it follows AR(1) stochastic process.
represents an intertemporal preference shock to the household’s current and future consumption and labour supply and it follows AR(1) stochastic process.
Next, let us turn to the budget constraint of the representative household. By supplying the labour inputs, 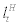 , to the entrepreneur, the representative household can earn the real wage, wt, for each unit of input. They can also deposit their final goods, bt, at period t and earn real interest rate,
, to the entrepreneur, the representative household can earn the real wage, wt, for each unit of input. They can also deposit their final goods, bt, at period t and earn real interest rate, 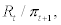 next period where Rt stands for gross nominal interest rate at period t and
next period where Rt stands for gross nominal interest rate at period t and 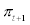 stands for gross inflation rate at period t + 1. Further, the household has access to the international financial market and can borrow the amount of
stands for gross inflation rate at period t + 1. Further, the household has access to the international financial market and can borrow the amount of 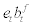 units of domestic final goods, where et stands for real exchange rate measuring the relative price of foreign goods in terms of domestic goods and
units of domestic final goods, where et stands for real exchange rate measuring the relative price of foreign goods in terms of domestic goods and 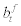 stands for the amount of foreign debt at period t. Next period, the household will repay the gross real interest rate of
stands for the amount of foreign debt at period t. Next period, the household will repay the gross real interest rate of 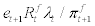 to the international financial market for each unit of foreign debt, where
to the international financial market for each unit of foreign debt, where 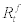 stands for gross foreign nominal interest rate,
stands for gross foreign nominal interest rate, 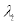 stands for country specific risk premium which is exogenous to the household’s decision,
stands for country specific risk premium which is exogenous to the household’s decision, 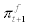 stands for gross foreign inflation rate in period t + 1. Finally, the household pays the lump sum tax of
stands for gross foreign inflation rate in period t + 1. Finally, the household pays the lump sum tax of 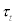 to the government and earns the combined dividend of
to the government and earns the combined dividend of 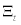 from domestic and imported goods wholesalers every period. Thus, the household’s budget constraint at period t can be expressed, in real terms, as follows,
from domestic and imported goods wholesalers every period. Thus, the household’s budget constraint at period t can be expressed, in real terms, as follows,
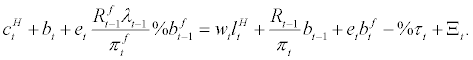 (2)
(2)
Given the above budget constraint (2), the representative household maximizes intertemporal utility function (1) with respect to 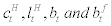 . The first order conditions for this dynamic optimization problem are:
. The first order conditions for this dynamic optimization problem are:
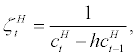 (3)
(3)
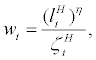 (4)
(4)
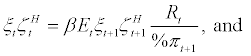 (5)
(5)
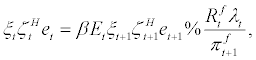 (6)
(6)
where 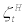 stands for the Lagrangian multiplier associated with the budget constraint (2). From equation. (3),
stands for the Lagrangian multiplier associated with the budget constraint (2). From equation. (3), 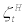 can be interpreted as the marginal utility of consumption at period t. Here, note that we used the property of external habit formation and the equilibrium condition,
can be interpreted as the marginal utility of consumption at period t. Here, note that we used the property of external habit formation and the equilibrium condition, 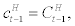 ; to derive equation. (3). equation. (4) is the first order condition with respect to
; to derive equation. (3). equation. (4) is the first order condition with respect to 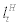 and it can be interpreted as the labour supply function by the household. equation. (5) is the first order condition (or Benveniste- Scheinkman equation) with respect to bt and can be interpreted as an implicit credit supply function by the household. It should be noted that intertemporal preference shock,
and it can be interpreted as the labour supply function by the household. equation. (5) is the first order condition (or Benveniste- Scheinkman equation) with respect to bt and can be interpreted as an implicit credit supply function by the household. It should be noted that intertemporal preference shock, 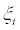 , affects the decision of credit supply (or saving) by the household significantly. For instance, if the ratio of intertemporal shocks,
, affects the decision of credit supply (or saving) by the household significantly. For instance, if the ratio of intertemporal shocks, 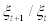 , is expected to be temporarily larger than one, the household will temporarily put higher weight on the future marginal utility,
, is expected to be temporarily larger than one, the household will temporarily put higher weight on the future marginal utility, 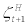 , and, therefore, decide to consume more in the future. In other words, in such situation, the household will decide to save more and supply more credit at current period. Thus, ratio of intertemporal shocks play an important role for the supply of credit, bt. Finally, equation. (6) is the first order condition (or Benveniste-Scheinkman equation) with respect to foreign debt,
, and, therefore, decide to consume more in the future. In other words, in such situation, the household will decide to save more and supply more credit at current period. Thus, ratio of intertemporal shocks play an important role for the supply of credit, bt. Finally, equation. (6) is the first order condition (or Benveniste-Scheinkman equation) with respect to foreign debt, 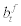 , and can be interpreted as an implicit foreign credit demand function by the household. By the same token, the ratio of intertemporal shocks affect the decision of foreign credit demand by the household significantly.
, and can be interpreted as an implicit foreign credit demand function by the household. By the same token, the ratio of intertemporal shocks affect the decision of foreign credit demand by the household significantly.
Entrepreneur’s problem
Individual entrepreneur’s problem: Following BGG, there is a continuum of entrepreneurs indexed by j∈[0,1] where each entrepreneur is risk neutral and has a finite expected horizon. As in BGG, these assumptions will ensure that each entrepreneur will not accumulate enough net worth to self-finance their new capital –i.e., each entrepreneur will rely on external finance to purchase new capital to some extent in equilibrium. In a spirit of CMR, each entrepreneur faces an exogenous time-varying stochastic survival rate of 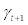 from period t to t + 1 which is common across all entrepreneurs5. We assume that the stochastic process of
from period t to t + 1 which is common across all entrepreneurs5. We assume that the stochastic process of 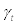 is uncorrelated with any other shocks in the economy and has its mean equal to γ – i.e.,=
is uncorrelated with any other shocks in the economy and has its mean equal to γ – i.e.,=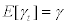 . . Between period t and t + 1, after
. . Between period t and t + 1, after 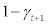 fraction of entrepreneurs have disappeared from the business, exactly the same amount of new entrepreneurs will enter the business so that the population of entrepreneurs in the economy remains the same from period t to t + 1. Each entrepreneur entering period t + 1 is endowed with fixed units of entrepreneurial labour,
fraction of entrepreneurs have disappeared from the business, exactly the same amount of new entrepreneurs will enter the business so that the population of entrepreneurs in the economy remains the same from period t to t + 1. Each entrepreneur entering period t + 1 is endowed with fixed units of entrepreneurial labour, 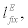 and receive compensation of
and receive compensation of 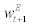 for each unit of labour.
for each unit of labour.
This endowment ensures the new entrepreneurs entering the intermediate goods industry to have strictly positive net worth to start up their business and issue their debts.
For 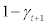 fraction of entrepreneurs who happened to exit the business between period t and t+1, they will sell off the capital they purchased at the end of period t and retire all of their debts before maturity6. They will simply consume their remaining net worth,
fraction of entrepreneurs who happened to exit the business between period t and t+1, they will sell off the capital they purchased at the end of period t and retire all of their debts before maturity6. They will simply consume their remaining net worth, 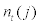 , and cease to exist from the economy at the beginning of period t + 1.
, and cease to exist from the economy at the beginning of period t + 1.
Turning to the production technology, each entrepreneur produces homogeneous domestic intermediate goods, 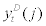 , and they are perfectly competitive when selling their products to the wholesalers. Each entrepreneur uses capital inputs and labour inputs and has a constant-return-to-scale technology in producing intermediate goods. Following Gertler, Gilchrist, and Natalucci [17], the production function7 for the intermediate goods is given by
, and they are perfectly competitive when selling their products to the wholesalers. Each entrepreneur uses capital inputs and labour inputs and has a constant-return-to-scale technology in producing intermediate goods. Following Gertler, Gilchrist, and Natalucci [17], the production function7 for the intermediate goods is given by
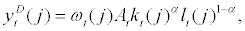 (7)
(7)
where 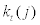 stands for capital holding by an entrepreneur j at period t and
stands for capital holding by an entrepreneur j at period t and 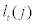 stands for labour inputs composed of household labour,
stands for labour inputs composed of household labour, 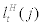 and entrepreneurial labour,
and entrepreneurial labour, 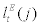 , which is defined as
, which is defined as
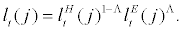 (8)
(8)
Here, it should be noted that the aggregate technology shock, At, is common across all entrepreneurs. Also, the capital share parameter, α, and the entrepreneurial labour share parameter, Λ , are common across all entrepreneurs as well. Following CF and BGG, we assume each entrepreneur is subject to an idiosyncratic shock, 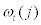 , which affects the total factor productivity of intermediate goods, yt(j). The idiosyncratic shock,
, which affects the total factor productivity of intermediate goods, yt(j). The idiosyncratic shock, 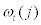 is a private information to entrepreneur j and assumed to be i.i.d. shock with mean equal to one –i.e.,
is a private information to entrepreneur j and assumed to be i.i.d. shock with mean equal to one –i.e., 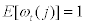 .
.
The corporate balance sheet of each entrepreneur at the end of period t can be expressed as
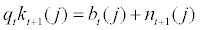 (9)
(9)
where qt stands for the relative price of capital, 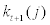 stands for the capital which will be used for production in period t + 1 but purchased at period t,
stands for the capital which will be used for production in period t + 1 but purchased at period t, 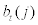 stands for the real debt issued at period t and
stands for the real debt issued at period t and 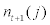 stands for the net worth at the end of period t. Basically, left-hand side of equation. (9) represents the total asset of the entrepreneur and right-hand side represents the liability and the net worth of the entrepreneur at the end of period t. As can be seen from this balance sheet equation, capital,
stands for the net worth at the end of period t. Basically, left-hand side of equation. (9) represents the total asset of the entrepreneur and right-hand side represents the liability and the net worth of the entrepreneur at the end of period t. As can be seen from this balance sheet equation, capital, 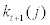 which is purchased at the end of period t is partially financed by issuing the debt,
which is purchased at the end of period t is partially financed by issuing the debt, 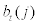 at period t. With the assumptions of risk neutrality and finite planning horizon, net worth (or internal finance) itself is never enough in financing the cost of capital purchase and, thus, each entrepreneur will rely on external finance in equilibrium.
at period t. With the assumptions of risk neutrality and finite planning horizon, net worth (or internal finance) itself is never enough in financing the cost of capital purchase and, thus, each entrepreneur will rely on external finance in equilibrium.
The corporate income statement (or using alternative accounting terminology; profit and loss statement) for entrepreneur j entering period t is specified as follows
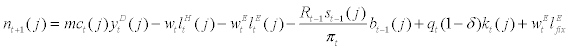 (10)
(10)
where mct(j) stands for marginal cost of intermediate goods j, wt stands for real wage of household labour, 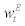 stands for real wage of entrepreneurial labour, parameter δ stands for capital depreciation rate, and St-1 stands for external finance premium charged by financial intermediary at period t-1. Each entrepreneur is a price-taker in the financial market and, thus, external finance premium is exogenously given to each entrepreneur8.
stands for real wage of entrepreneurial labour, parameter δ stands for capital depreciation rate, and St-1 stands for external finance premium charged by financial intermediary at period t-1. Each entrepreneur is a price-taker in the financial market and, thus, external finance premium is exogenously given to each entrepreneur8.
Let us look at the corporate income statement more closely. At the beginning of period t, each entrepreneur will use capital 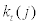 – which was purchased at the end of period t-1 – and employ household and entrepreneurial labour. Then, each entrepreneur will produce intermediate goods j according to production function (7) and sell them off to the wholesalers in a perfectly competitive manner. Thus, the revenue for each entrepreneur will be equal to marginal cost multiplied by the amount of intermediate goods produced as can be seen in equation. (10). Each entrepreneur will pay the labour cost and also repay the debt to financial intermediary. The gross repayment rate is given by
– which was purchased at the end of period t-1 – and employ household and entrepreneurial labour. Then, each entrepreneur will produce intermediate goods j according to production function (7) and sell them off to the wholesalers in a perfectly competitive manner. Thus, the revenue for each entrepreneur will be equal to marginal cost multiplied by the amount of intermediate goods produced as can be seen in equation. (10). Each entrepreneur will pay the labour cost and also repay the debt to financial intermediary. The gross repayment rate is given by 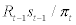 which includes the external finance premium in addition to the realized real interest rate. Finally, each entrepreneur will sell off depreciated capital to the capital market earning
which includes the external finance premium in addition to the realized real interest rate. Finally, each entrepreneur will sell off depreciated capital to the capital market earning 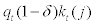 and provide endowed entrepreneurial labour to other entrepreneurs earning
and provide endowed entrepreneurial labour to other entrepreneurs earning 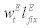 as an income. The net income after these activities are captured by
as an income. The net income after these activities are captured by 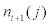 and will be a net worth for the entrepreneur j at the end of period t. Given this net worth, each entrepreneur will plan for the next period and decide how much capital to purchase and how much debt to issue at the end of period t as we have seen in balance sheet equation (9).
and will be a net worth for the entrepreneur j at the end of period t. Given this net worth, each entrepreneur will plan for the next period and decide how much capital to purchase and how much debt to issue at the end of period t as we have seen in balance sheet equation (9).
For each entrepreneur entering period t, they will maximize their expected discounted sum of profits by choosing capital inputs, labor inputs, and debt issuance subject to equation. (7), (8), (9), and (10). The first order conditions for each entrepreneur j are given by
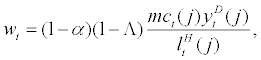 (11)
(11)
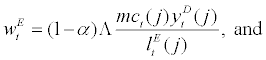 (12)
(12)
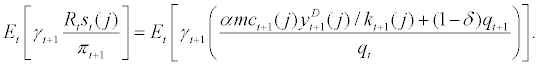 (13)
(13)
Equation. (11) equates marginal cost of employing household labour to marginal product of household labour. This equation can be thought of as a demand function for household labour by entrepreneur j. By the same token, equation. (12) can be thought of as a demand function for entrepreneurial labour. Equation. (13) equates the expected marginal cost of capital financed by debt to the expected marginal return of capital financed by debt and can be thought of as the Euler equation of capital for entrepreneur j. Since stochastic survival rate, γt+1, is uncorrelated to any other shocks in the economy, equation. (13) can be further rearranged which is the standard result as in BGG. Thus, the introduction of stochastic survival rate will not alter the Euler equation of capital for any entrepreneur j compared to the case with constant survival rate as in BGG.
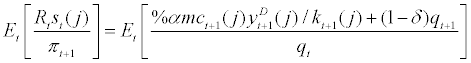 (14)
(14)
Financial intermediary: We now turn to the financial intermediary’s problem9. Following BGG, the idiosyncratic total factor pro-ductivity shock, 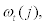 is private information for entrepreneur j that there exists information asymmetry between entrepreneur (borrower) and financial intermediary (lender). Due to costly state verification, the financial intermediary cannot observe entrepreneur j’s output,
is private information for entrepreneur j that there exists information asymmetry between entrepreneur (borrower) and financial intermediary (lender). Due to costly state verification, the financial intermediary cannot observe entrepreneur j’s output, 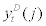 , costlessly, but need to incur a fixed monitoring cost to observe entrepreneur’s output. The entrepreneur, after observing project outcome, will decide whether to repay the debt or default at period t. If the entrepreneur decides to repay, the financial intermediary will receive gross repayment of
, costlessly, but need to incur a fixed monitoring cost to observe entrepreneur’s output. The entrepreneur, after observing project outcome, will decide whether to repay the debt or default at period t. If the entrepreneur decides to repay, the financial intermediary will receive gross repayment of 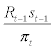 for each unit of credits outstanding at period t regardless of the realization of idiosyncratic shock,
for each unit of credits outstanding at period t regardless of the realization of idiosyncratic shock, 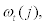 . On the other hand, if the entrepreneur decides to default, the financial intermediary will pay a fixed monitoring cost to observe
. On the other hand, if the entrepreneur decides to default, the financial intermediary will pay a fixed monitoring cost to observe 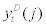 and seize the project outcome from the entrepreneur.
and seize the project outcome from the entrepreneur.
Under this problem set up, BGG shows that the optimal debt contract implies that the external finance premium, st, to depend upon the entrepreneur’s overall balance sheet condition. Specifically, they show that the external finance premium to be a function of the leverage ratio and increasing with respect to the ratio. The reduced form function can be characterized by
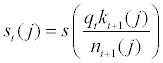 (15)
(15)
where sI (.) > 0 and s(1) = 0.
For estimation purpose, we follow Covas and Zhang [18] and Dib et al. [19] and adopt the following functional form
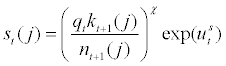 (16)
(16)
where parameter χ can be interpreted as the elasticity of external finance premium with respect to the leverage ratio and is strictly positive and 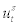 stands for an exogenous external finance premium shock which is common across all entrepreneurs. Thus, for the empirical purpose of this paper, the movement in external finance premium can be decomposed into two factors –1) a movement due to a change in the leverage ratio
stands for an exogenous external finance premium shock which is common across all entrepreneurs. Thus, for the empirical purpose of this paper, the movement in external finance premium can be decomposed into two factors –1) a movement due to a change in the leverage ratio 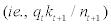 which is endogenously determined in the model and 2) a movement due to a change in the external finance premium shock
which is endogenously determined in the model and 2) a movement due to a change in the external finance premium shock 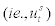 which is exogenously given outside of the model.
which is exogenously given outside of the model.
Aggregate net worth transition: As shown by CF and BGG, the assumptions of constant-return-to-scale production technology and risk neutrality will render marginal product of labour, marginal product of capital, marginal cost, and leverage ratio to be equal across all solvent entrepreneurs in equilibrium10. Further, since bankruptcy cost is constant-return-to-scale and leverage ratio are equal for all j, the external finance premium will be equal across all solvent entrepreneurs in equilibrium. This property will make aggregation very simple which renders equation. (11), equation. (12), equation. (14), and equation. (15) to hold in aggregate level as well.
Next, we derive the law of motion of the aggregate net worth. Aggregating over corporate income statement equation. (10) and taking into account of stochastic survival rate of entrepreneurs from period t 1 to t, we obtain the following aggregate net worth transition equation11.
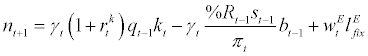 (17)
(17)
where realized gross return from capital, 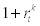 , is defined as
, is defined as
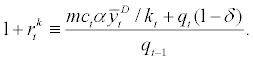
And 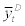 stands for the average of realized
stands for the average of realized 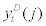 across all entrepreneurs. By normalizing
across all entrepreneurs. By normalizing 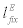 to one and using corporate balance sheet equation (9), equation. (17) can be rearranged as
to one and using corporate balance sheet equation (9), equation. (17) can be rearranged as
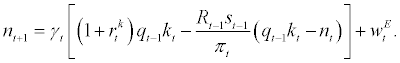 (18)
(18)
Finally, aggregate consumption of entrepreneurs going out of business can be expressed as
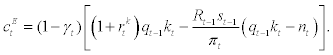 (19)
(19)
Capital producer’s problem
We now turn to a capital producer’s problem. Capital producers are perfectly competitive and risk neutral. They purchase 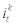 amount of final goods from the retailer, convert them to
amount of final goods from the retailer, convert them to 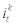 amount of capital goods, and combine them with existing capital stock (purchased from entrepreneurs),
amount of capital goods, and combine them with existing capital stock (purchased from entrepreneurs), 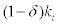 , to produce new capital stock,
, to produce new capital stock, 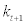 . Capital producers will, then, sell off new capital stock to entrepreneurs in a perfectly competitive manner. Capital producers have linear production technology in converting final goods to capital goods. However, following CEE and SW, when they change the production capacity of capital goods from previous period, they will incur quadratic investment adjustment cost. Given this set up, the profit function for each capital producer at period t can be expressed as follows,
. Capital producers will, then, sell off new capital stock to entrepreneurs in a perfectly competitive manner. Capital producers have linear production technology in converting final goods to capital goods. However, following CEE and SW, when they change the production capacity of capital goods from previous period, they will incur quadratic investment adjustment cost. Given this set up, the profit function for each capital producer at period t can be expressed as follows,
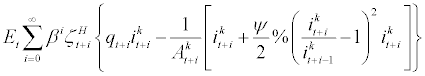 (20)
(20)
Where 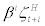 stands for discount factor imposed by the representative household who owns the firm,
stands for discount factor imposed by the representative household who owns the firm, 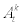 stands for investment specific technology shock and
stands for investment specific technology shock and 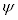 stands for adjustment cost parameter. Each capital producer will maximize the expected discounted sum of the profits with respect to
stands for adjustment cost parameter. Each capital producer will maximize the expected discounted sum of the profits with respect to 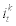 . The first order condition is given by
. The first order condition is given by
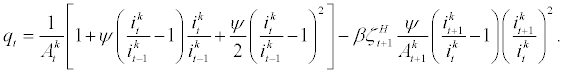 (21)
(21)
Finally, aggregate capital accumulation equation is given by
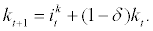 (22)
(22)
Wholesaler and retailer’s problem
Wholesaler of domestic intermediate goods: Here, we describe the optimal price setting behavior of the continuum of wholesalers of domestic intermediate goods, 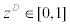 who purchase domestic intermediate goods at perfectly competitive price from the entrepreneurs and resale them monopolistically (perhaps by attaching their brand name zD) in the wholesale market. The demand function for domestic intermediate goods sold by the wholesaler zD is given by
who purchase domestic intermediate goods at perfectly competitive price from the entrepreneurs and resale them monopolistically (perhaps by attaching their brand name zD) in the wholesale market. The demand function for domestic intermediate goods sold by the wholesaler zD is given by
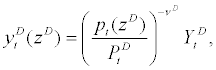
where 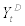 stands for CES-aggregated domestic intermediate goods à la Dixit-Stiglitz,
stands for CES-aggregated domestic intermediate goods à la Dixit-Stiglitz, 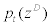 stands for nominal price of intermediate goods
stands for nominal price of intermediate goods 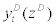 ,
, 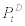 stands for aggregate price index of domestic intermediate goods
stands for aggregate price index of domestic intermediate goods 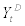 , and parameter
, and parameter 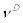 stands for the relative price elasticity for
stands for the relative price elasticity for 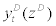 . We assume Calvo [21] - Yun [22] type sticky price setting for the wholesaler where, for any given period t, fraction
. We assume Calvo [21] - Yun [22] type sticky price setting for the wholesaler where, for any given period t, fraction 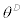 of the entire wholesalers cannot freely revise their price. Further, following the treatment of CEE [23] and Smets and Wouters [6,7] in modelling inflation persistence12, we allow for the partial indexation for the wholesalers who were not able to revise their prices freely at period t. In particular,
of the entire wholesalers cannot freely revise their price. Further, following the treatment of CEE [23] and Smets and Wouters [6,7] in modelling inflation persistence12, we allow for the partial indexation for the wholesalers who were not able to revise their prices freely at period t. In particular, 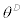 fraction of the wholesalers who did not receive a ‘signal of price change’ will partially index their price to lagged inflation of domestic intermediate goods as follows,
fraction of the wholesalers who did not receive a ‘signal of price change’ will partially index their price to lagged inflation of domestic intermediate goods as follows,
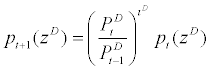
where parameter 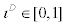 controls the magnitude of indexation to the past inflation rate.
controls the magnitude of indexation to the past inflation rate.
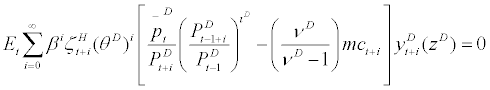
where 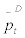 stands for the optimal price chosen by the ‘price changing’ wholesalers at period t,
stands for the optimal price chosen by the ‘price changing’ wholesalers at period t, 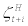 stands for marginal utility of consumption by the household at period t + i, and mct+i stands for the purchasing cost of domestic intermediate goods from the entrepreneurs which are purchased at perfectly competitive price (i.e., the real cost of purchase equals marginal cost of producing domestic intermediate goods) at period t + i. From the definition of the aggregate price index, it can be shown that the law of motion of PDt to be as follows
stands for marginal utility of consumption by the household at period t + i, and mct+i stands for the purchasing cost of domestic intermediate goods from the entrepreneurs which are purchased at perfectly competitive price (i.e., the real cost of purchase equals marginal cost of producing domestic intermediate goods) at period t + i. From the definition of the aggregate price index, it can be shown that the law of motion of PDt to be as follows
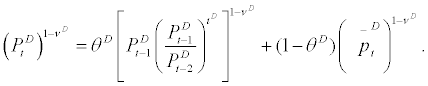
Wholesaler of imported intermediate goods: The optimal price setting behavior by the wholesalers of imported intermediate goods will be similar to that of domestic wholesalers. There is a continuum of imported goods wholesalers, 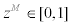 , who purchase imported intermediate goods at the purchasing cost equal to real exchange rate, et, and resell them monopolistically in the wholesale market. The demand function for imported intermediate goods sold by the wholesaler zM is given by
, who purchase imported intermediate goods at the purchasing cost equal to real exchange rate, et, and resell them monopolistically in the wholesale market. The demand function for imported intermediate goods sold by the wholesaler zM is given by
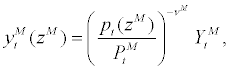
where 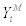 stands for CES-aggregated imported intermediate goods,
stands for CES-aggregated imported intermediate goods, 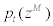 stands for nominal price of imported intermediate goods,
stands for nominal price of imported intermediate goods, 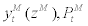 stands for aggregate price index of imported intermediate goods
stands for aggregate price index of imported intermediate goods 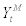 , and parameter
, and parameter 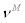 stands for the relative price elasticity for
stands for the relative price elasticity for 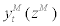 . By the same token as in domestic intermediate goods, we assume Calvo-Yun type sticky price setting where fraction
. By the same token as in domestic intermediate goods, we assume Calvo-Yun type sticky price setting where fraction 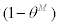 of the wholesalers of imported intermediate goods can freely re-optimize their prices at any given period t. For the rest of fraction
of the wholesalers of imported intermediate goods can freely re-optimize their prices at any given period t. For the rest of fraction 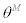 of the wholesalers, they will partially index their price to lagged inflation of imported intermediate goods as follows,
of the wholesalers, they will partially index their price to lagged inflation of imported intermediate goods as follows,
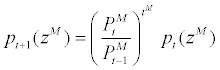
where parameter 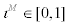 controls the magnitude of indexation.
controls the magnitude of indexation.
Under this setting, 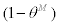 fraction of the wholesalers at period t will set the price such that
fraction of the wholesalers at period t will set the price such that
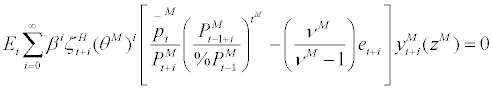
where 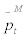 stands for the optimal price by the imported goods wholesalers who re-optimize at period t and et+i stands for the real exchange rate which is equal to the purchasing cost of the imported intermediate goods at period t + i. Thus, the only difference (except for the parameter values and superscripts) between domestic wholesalers and imported goods wholesalers is the purchasing cost of the intermediate goods. The domestic wholesalers pay the marginal cost of producing domestic intermediate goods as the purchasing cost, while the wholesalers of imported goods pay the real exchange rate as the purchasing cost.
stands for the optimal price by the imported goods wholesalers who re-optimize at period t and et+i stands for the real exchange rate which is equal to the purchasing cost of the imported intermediate goods at period t + i. Thus, the only difference (except for the parameter values and superscripts) between domestic wholesalers and imported goods wholesalers is the purchasing cost of the intermediate goods. The domestic wholesalers pay the marginal cost of producing domestic intermediate goods as the purchasing cost, while the wholesalers of imported goods pay the real exchange rate as the purchasing cost.
Again, from the definition of the aggregate price index, it can be shown that the law of motion of 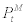 to be as follows
to be as follows
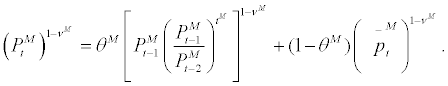
Retailer of final goods: Next, we describe the behavior of the final good retailer. The retailer combines domestic intermediate goods and imported intermediate goods to form the final goods, Yt, using the following CES aggregation Technology
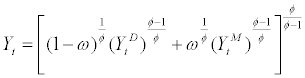
where parameter  stands for the share of imported goods in the final goods production and parameter φ stands for the elasticity of substitution between domestic intermediate goods and imported intermediate goods. The retailer is perfectly competitive in the final goods market and the cost mini-mization yields the following demand functions for
stands for the share of imported goods in the final goods production and parameter φ stands for the elasticity of substitution between domestic intermediate goods and imported intermediate goods. The retailer is perfectly competitive in the final goods market and the cost mini-mization yields the following demand functions for  and
and 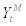 ;
;
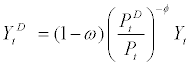
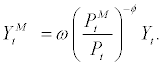
Finally, the price index, Pt, corresponding to to the final goods can be shown to be as follow
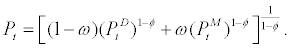
Small open economy features
Here, we describe the small-open economy feature of the model. Substituting equation. (5) into equation. (6) and log-linearization around the steady state yields a modified version of the uncovered interest rate parity condition
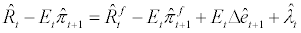
where the log-deviation from the steady state is denoted by the hatform. Following Adolfson et al. [25], the country risk premium is assumed to depend on the level of the net foreign debt and the changes in the real exchange rate as follows
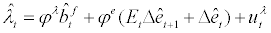
where parameters 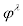 and
and 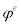 control the sensitivity of country risk premium in response to the level of net foreign debt and changes in real exchange rate and
control the sensitivity of country risk premium in response to the level of net foreign debt and changes in real exchange rate and 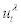 is an AR(1) exogenous shock to the country risk premium.
is an AR(1) exogenous shock to the country risk premium.
The demand of final goods by the foreign sector, 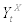 , which is to be exported to foreign sector is given By
, which is to be exported to foreign sector is given By
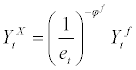
where the inverse of real exchange rate stands for the relative price of Canadian final goods in terms of foreign goods, parameter 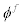 stands for the relative price elasticity of exported final goods, and
stands for the relative price elasticity of exported final goods, and 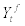 stands for foreign GDP.
stands for foreign GDP.
The balance of payment accounting identity is given as
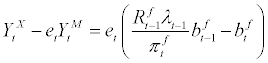
where the left-hand side stands for the trade surplus and the right-hand side stands for foreign investment income deficit combined with the change in net foreign debt position. By the accounting identity, both sides should be balanced as above.
In order to keep the foreign sector as simple as possible, we assume ARMA (1,1) process for log-linearized foreign GDP, foreign inflation, and foreign interest rate as follows:

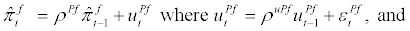
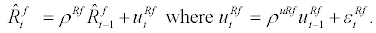
Thus, the structure of the foreign sector is exogenous to the domestic sector – i.e., the exogenous shock originating in the foreign sector will affect Canadian endogenous variables, but the shock originating in the Canadian sector will not affect foreign variables.
The rest of the model structure
In closing the model, we describe the rest of the model structure here. The central bank is assumed to follow a simple Taylor-type monetary policy rule and the nominal interest rate is adjusted in response to inflation gap and GDP gap with some interest rate smoothing. In the log-deviation form, the monetary policy rule is specified as follow
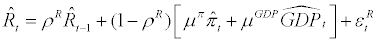 (23)
(23)
where parameter 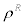 controls the magnitude of interest smoothing, parameter
controls the magnitude of interest smoothing, parameter 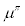 stands for the Taylor coefficient in response to inflation gap,
stands for the Taylor coefficient in response to inflation gap, 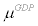 stands for the Taylor coefficient in response to GDP gap (the variable GDPt will be defined shortly), and
stands for the Taylor coefficient in response to GDP gap (the variable GDPt will be defined shortly), and 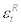 stands for i.i.d. monetary policy shock. The central bank is assumed to react to the short-run inflation gap which is a deviation of inflation rate from the inflation target.
stands for i.i.d. monetary policy shock. The central bank is assumed to react to the short-run inflation gap which is a deviation of inflation rate from the inflation target.
The government budget constraint is specified as
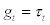 (24)
(24)
which is simply saying that the government expenditure, 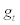 , is financed solely by lump-sum tax,
, is financed solely by lump-sum tax, 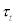 , which appears in the representative household’s budget constraint equation. (2). Thus, the government is assumed to operate on a balanced budget every period without accumulating debt (or assets) over time.
, which appears in the representative household’s budget constraint equation. (2). Thus, the government is assumed to operate on a balanced budget every period without accumulating debt (or assets) over time.
Next, the market clearing condition for final goods is given as follows
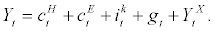 (25)
(25)
Now, it should be noted that the above market clearing condition does not conform with the definition of (real) GDP since the net export does not appear in the equation. In order to conform with the definition of real GDP (which will be the observed data in the estimation), we define the auxiliary variable, GDPt, by subtracting the value of imported intermediate goods from the value of final goods as follow
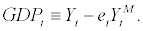 (26)
(26)
We use this auxiliary variable, GDPt, to match the actual real GDP data in our estimation section.
The shock structure
There are a total of 12 shocks specified in the model categories: financial shocks and non-financial shocks. the log-linearized form, as follows:
Financial shocks
Aggregate net worth shock 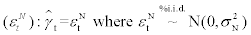
External finance premium shock 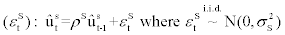
Non-Financial Shocks
Aggregate technology shock 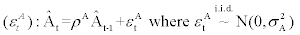
Intertemporal preference shock 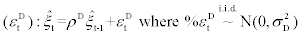
Government expenditure shock 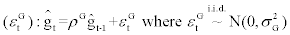
Investment-specific tech. shock 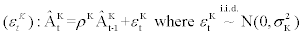
Country risk premium shock 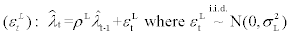
Marginal cost shock 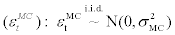
Monetary policy shock 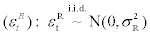
Foreign inflation shock 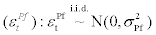
Foreign interest rate shock 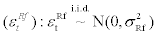
Foreign GDP shock 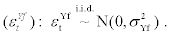
Motivation of having two financial shocks in the model
As we have seen in Section 2, in addition to standard macroeconomic shocks adopted in the empirical DSGE literature, we adopt two types of financial shocks in this paper: 1) external finance premium shock and 2) aggregate net worth shock. The importance of the external finance premium shock has been pointed out by Smets and Wouters [6,7]13 and Dib et al. [19], among others. In a similar fashion, CMR emphasized the importance of the role of the aggregate net worth shock14 to economic fluctuations based on U.S. data. Considering the potential importance of both financial shocks to the Canadian business cycle, the approach of this paper is to incorporate only one or both or even none of the financial shocks in the estimation models and to assess the relative importance of the two shocks.
In our model setup, an intrinsic difference between the external finance premium shock and the aggre-gate net worth shock is as follows: the former shock directly affects the financing cost of capital goods, but does not affect the balance sheet of the entrepreneurs directly, whereas the latter shock affects the aggregate net worth directly, which in turn affects the financing cost of capital goods via change in leverage ratio. In other words, the former shock is an exogenous shock to the financing cost, whereas the latter shock is an exogenous shock to the aggregate net worth position which, in turn, affects the financing cost endogenously. In a sense that the external finance premium shock affects the external finance premium (or credit spread) regardless of the conditions in corporate balance sheets, this shock can be interpreted as a shock occurring in the financial market or a shock to financial intermediary’s lending attitude. Likewise, the aggregate net worth shock can be interpreted as a shock occurring in the corporate sector affecting the aggregate net worth position of the economy.
In order to compare the relative importance (or unimportance) of these two financial shocks, we estimate several versions of the model specified in Section 2. Specifically, we employ four versions of empirical models where 1) there are no financial shocks in the model (referred as NoFin-Shock model), 2) the aggregate net worth shock is the only financial shock in the model (referred as eN-only model), 3) the external finance premium shock is the only financial shock in the model (referred as eS-only model), and 4) both shocks are incorporated into the model (referred as Full-Shock model).
Motivation of the usage of financial data
In addition to the standard macroeconomic data, such as GDP, consumption, business fixed investment, inflation rate, etc., used in the empirical DSGE literature (such as in SW and Adolfson et al. [25], among others), we use additional financial data to estimate the model. Since the main objective of this paper is to assess the link of financial variables and shocks to real economic activity in the Canadian business cycle, it is imperative that we include some additional financial data to identify the shocks and, further, to assess the financial shock propagation mechanism more accurately. Following CMR, we include credit spread data as a proxy for external finance premium. Provided that credit spread data is a good proxy of the external finance premium, inclusion of such data should help assessing the dynamic linkage (if any) between the external finance premium and business fixed investment more accurately.
In addition to credit spread data, we add another financial data for model estimation. Specifically, we include leverage ratio data from the National Balance Sheet Accounts as a proxy for the leverage defined in the model. The reason for this inclusion is as follows. There are two financial shocks in the benchmark model in this paper: external premium shock and aggregate net worth shock. As we will see later in the estimation section, both shocks imply qualitatively similar, if not quantitatively, shape of impulse response functions for the non-financial variables such as GDP, consumption, business fixed investment, capital price, inflation, and trade surplus. Further, even for impulse response functions of external finance premium, both shocks imply qualitatively similar shape. Thus, if the observable variables are confined to these variables, it will be difficult, if not impossible, to discern the external finance premium shock from the aggregate net worth shock from the observed data. In order to facilitate identification of two shocks, we include additional financial data, such as leverage ratio data, for the model estimation.
Data description
We estimate the model using 12 series of quarterly Canadian and U.S. data: Canadian GDP, consumption expenditure, business fixed investment, inflation rate, trade surplus, U.S.-Canada real exchange rate, yield spread, credit spread, leverage ratio, U.S. GDP, U.S. inflation, and U.S. nominal interest rate. Due to the availability of leverage ratio data, the sample period spans from 1990Q1 to 2007Q4 (total 72 observations).
The data series of Canadian GDP, consumption expenditure, business fixed investment, and trade surplus are from Statistics Canada’s National Income and Expenditure Accounts (NIEA). All the expenditure series are measured in seasonally adjusted, real terms, and per capita base using Canadian population aged 15 years and above. Consumption expenditure is measured by real personal expenditure on consumer goods and services, while business fixed investment is measured by non-residential structures and equipment. The series for trade surplus is constructed from exports and imports measured by goods and services. Canadian inflation rate is based on the Bank of Canada’s measure of core-CPI index, excluding eight most volatile components of CPI and adjusted for indirect tax effects.
The data series of credit spread is based on the index15 of BBB medium term corporate bond spread vis-à-vis medium term government bond. This credit spread data will be matched to the model’s external finance premium, st16. The data series of leverage ratio is simply the ratio of total asset over net worth where both data are adopted from the National Balance Sheet Accounts (NBSA, nonfinancial corporations including government business enterprises). This leverage ratio data will be matched to the model’s leverage ratio, 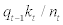 , with some measurement error. Again, it should be noted that, due to the data restriction arising from the NBSA, the sample period of leverage ratio is confined to 1990Q1 to 2007Q4.
, with some measurement error. Again, it should be noted that, due to the data restriction arising from the NBSA, the sample period of leverage ratio is confined to 1990Q1 to 2007Q4.
The data series of U.S. GDP is from the U.S. National Income and Product Accounts (NIPA) and is measured in seasonally adjusted, real terms, and per capita base using U.S. total population. U.S. inflation rate is based on seasonally adjusted U.S. core-CPI, excluding food and energy components. U.S. nominal interest rate is measured by the U.S. Federal Funds target rate. U.S.-Canada real exchange rate is calculated as the nominal exchange rate (Canadian$/US$) multiplied by the ratio of U.S. CPI over Canadian CPI. Thus, the U.S.-Canada real exchange rate measures the relative price of U.S. goods and services in terms of Canadian goods and services which is consistent with the unit of real exchange rate, et, defined in this paper.
The data series for yield spread is calculated by subtracting the yield rate from a 10-year Government of Canada Bond from the interbank overnight rate, which is the policy instrument for the Bank of Canada. Then, this yield spread data is matched with the variable R in the model according to the following equation
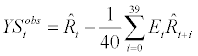 (27)
(27)
where 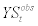 stands for yield spread data observed at period t. The reason why we do not simply match the overnight rate to
stands for yield spread data observed at period t. The reason why we do not simply match the overnight rate to 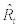 is that
is that 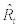 in the model represents the (log) deviation of short-term nominal interest rate from its steady state
in the model represents the (log) deviation of short-term nominal interest rate from its steady state 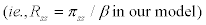 . Now, if, in reality, the expected inflation rate is stationary over time without having any trend, then usage of overnight rate data can be justified by matching model’s
. Now, if, in reality, the expected inflation rate is stationary over time without having any trend, then usage of overnight rate data can be justified by matching model’s 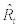 to the demeaned overnight rate data. Unfortunately, however, the expected inflation rate may possess a trend over time. In order to match the overnight rate data with the model’s
to the demeaned overnight rate data. Unfortunately, however, the expected inflation rate may possess a trend over time. In order to match the overnight rate data with the model’s 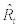 , then, it requires appropriate detrending which is a formidable task to attain. Rather, in our paper, we take a different path and construct the yield spread by subtracting 10-year government bond yield from the overnight rate. Under the assumption that the term premium on a 10-year bond is appropriately eliminated17 and the expected inflation component being cancelled out by subtraction, the yield spread data represents the gap between the short-term monetary policy stance and long-term (or 10-year-averaged) monetary policy stance. In our model, this gap can be formulated by the right hand side of equation. (27). Similar methodology has been adopted by De Graeve et al. and Wouters.
, then, it requires appropriate detrending which is a formidable task to attain. Rather, in our paper, we take a different path and construct the yield spread by subtracting 10-year government bond yield from the overnight rate. Under the assumption that the term premium on a 10-year bond is appropriately eliminated17 and the expected inflation component being cancelled out by subtraction, the yield spread data represents the gap between the short-term monetary policy stance and long-term (or 10-year-averaged) monetary policy stance. In our model, this gap can be formulated by the right hand side of equation. (27). Similar methodology has been adopted by De Graeve et al. and Wouters.
Finally, the structure of the model assumes that all the variables possess a stationary processes around the steady states. Further, since we log-linearize the model around the steady state and convert all the variables into the log-deviation form with mean zero, the observed data need to be transformed accordingly. Specifically, we (log) linearly detrend the following series; Canadian GDP, consumption expenditure, business fixed investment, trade surplus, real exchange rate and U.S. GDP. Also, we demean the following series; Canadian inflation18, yield spread, credit spread, U.S. inflation, and U.S. nominal interest rate.
Measurement errors
We allow for the existence of measurement errors for the following variables: trade surplus and leverage ratio. The reason is purely empirical. For the trade surplus data series adopted from NIEA, it includes the trade surplus from the U.S. as well as the rest of the world. However, the foreign GDP, foreign inflation, and foreign interest rate in the model are matched to the U.S. data only that there may be a discrepancy between the model’s definition of trade surplus vis-a-vis the actual trade surplus from the data. In order to subdue the effect from this possible discrepancy empirically, we impose the measurement error to the model’s definition of trade surplus as follows
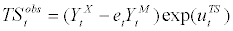
where 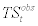 stands for the observed trade surplus data and uTSt stands for the measurement error for the trade surplus. We allow the measurement error to follow AR(1) process as follows;
stands for the observed trade surplus data and uTSt stands for the measurement error for the trade surplus. We allow the measurement error to follow AR(1) process as follows;
Measurement error in trade surplus
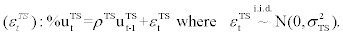
The reason for imposing measurement errors on leverage ratio is similar. For leverage ratio, we adopt the data from the NBSA where the definition of the asset, liability and net worth may be different from the model’s definitions of those variables. Again, in order to subdue the possible empirical effects arising from these discrepancies, we impose the measurement errors to the model’s definition of leverage ratio as Follows
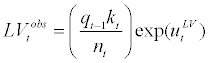
where 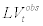 stand for observed leverage ratio data and
stand for observed leverage ratio data and 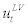 stand for the measurement errors for leverage ratio. Again, we allow the measurement error to follow AR(1) process as follow;
stand for the measurement errors for leverage ratio. Again, we allow the measurement error to follow AR(1) process as follow;
Measurement error in leverage ratio
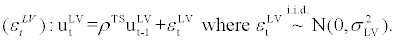
Calibrated parameters and Priors
We calibrate the subset of the parameters in the model that are not identifiable (i.e., the parameters only pertinent to the steady states) or are difficult to identify from the observed data. Calibrated parameters are reported in Table 1. From Christensen and Dib [8], the discount factor,β , is set to 0.9928, the capital share,α , is set to 0.3384, and the capital depreciation rate,δ , is set to 0.025. Following BGG, the survival rate of the entrepreneurs,γ , is set to 0.9728. Likewise, the specification of the priors are reported in Table 2.
| Parameters | Description | Values |
|---|---|---|
| β | discount factor | 0.9928 |
| α | capital share in production | 0.3384 |
| γ | mean survival rate of entrepreneurs | 0.9728 |
| δ | capital depreciation rate | 0.025 |
| ω | share of imported goods in final goods production | 0.2479 |
| φ | elasticity of substitution between domestic and imported goods | 1 |
| ƲD | relative price elasticity of domestic goods | 20 |
| ƲM | relative price elasticity of imported goods | 20 |
| ρIT | persistence parameter of in‡ation target shock | 0.975 |
| π* | gross steady state in‡ation target | 1.005 |
| kss=nss | steady state leverage ratio | 1.991 |
| gss/GDPss | steady state ratio of government expenditure to GDP | 0.2201 |
Table 1: Calibrated Parameters.
| Parameters | Description | Dist. Type | Mean | Std. |
|---|---|---|---|---|
| µπ | Taylor coefficient of inflation gap | gamma | 2 | 0.5 |
| µGDP | Taylor coefficient of GDP gap | gamma | 0.5 | 0.25 |
| h | habit formation parameter | beta | 0.5 | 0.25 |
| η | elasticity of labour supply | gamma | 0.5 | 0.35 |
| Χ | elasticity of external Finance premium | inv. gamma | 0.05 | 0.025 |
| Ψ | investment adjustment cost parameter | gamma | 1 | 0.5 |
| θD | Calvo parameter for domestic goods | beta | 0.5 | 0.25 |
| θM | Calvo parameter for imported goods | beta | 0.5 | 0.25 |
| ɭ D | in‡ation persistence param. for domestic goods | beta | 0.5 | 0.25 |
| ɭ M | in‡ation persistence param. for imported goods | beta | 0.5 | 0.25 |
| φe | elasticity of country risk premium w.r.t. Δ e | beta | 0.5 | 0.25 |
| φλ | elasticity of country risk premium w.r.t. bf | inv. gamma | 0.001 | Inf |
| φf | relative price elasticity of exported goods | gamma | 2 | 0.75 |
| all ρ ’s | all AR(1) persistence parameters | beta | 0.5 | 0.25 |
| all σ ’s | std. deviation for all shocks | inv. gamma | 0.01 or 0.001 | Inf |
Table 2: Specification of the Priors.
Posteriors
Table 3a reports the posterior distributions of the parameters for the benchmark model described in Section 2. For the sake of comparison, the estimation results for three alternative versions of the model are reported as well – i.e., 1) the model without financial shocks (denoted NoFin-Shock model, hereafter), 2) the model with only aggregate net worth shock as financial shock (denoted eN-only model, hereafter), and 3) the model with only external finance premium shock as financial shock (denoted eS-only model, hereafter). It should be noted that, here, the basic structure of four models are exactly the same, except for the specification of the financial shocks. The idea in comparing the estimation result of the benchmark model against those from three different models is to see whether the estimation result is sensitive to the specification of the financial shock structure.
| Full Shocks | eN Shock Only | eS Shock Only | No Fin Shock | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | Prior | Post. | 5% Conf. |
95% Conf. |
Dist. | Prior | Post. | 5% Conf. | 95% Conf. | Dist. | Prior | Post. | 5% Conf. | 95% Conf. | Dist. | Prior | Post. | 5% Conf. | 95% Conf. | Prior |
| Mean | Mean | Mean | Mean | Mean | Mean | Mean | Mean | Dist. | ||||||||||||
| rho_A | 0.5 | 0.9926 | 0.9856 | 0.9997 | beta | 0.5 | 0.9743 | 0.9503 | 0.999 | beta | 0.5 | 0.9913 | 0.9827 | 0.9995 | beta | 0.5 | 0.9846 | 0.9717 | 0.9984 | beta |
| rho_Ak | 0.5 | 0.3674 | 0.1892 | 0.5453 | beta | 0.5 | 0.4698 | 0.2991 | 0.6552 | beta | 0.5 | 0.4279 | 0.2585 | 0.5974 | beta | 0.5 | 0.617 | 0.4843 | 0.767 | beta |
| rho_lambda | 0.5 | 0.9482 | 0.9322 | 0.9651 | beta | 0.5 | 0.9517 | 0.9348 | 0.9692 | beta | 0.5 | 0.9477 | 0.9316 | 0.9631 | beta | 0.5 | 0.9597 | 0.9413 | 0.9763 | beta |
| rho_ED | 0.5 | 0.7266 | 0.6253 | 0.8366 | beta | 0.5 | 0.7045 | 0.5356 | 0.8823 | beta | 0.5 | 0.7209 | 0.6035 | 0.8367 | beta | 0.5 | 0.7138 | 0.5761 | 0.86 | beta |
| rho_S | 0.5 | 0.9179 | 0.8577 | 0.9756 | beta | N/A | N/A | N/A | N/A | N/A | 0.5 | 0.9354 | 0.8894 | 0.9864 | beta | N/A | N/A | N/A | N/A | N/A |
| rho_EG | 0.5 | 0.8945 | 0.8375 | 0.9507 | beta | 0.5 | 0.8717 | 0.815 | 0.9366 | beta | 0.5 | 0.8856 | 0.819 | 0.9537 | beta | 0.5 | 0.8492 | 0.7885 | 0.9104 | beta |
| rho_Yf | 0.5 | 0.6412 | 0.3272 | 0.9716 | beta | 0.5 | 0.6565 | 0.3475 | 0.9562 | beta | 0.5 | 0.6591 | 0.3517 | 0.9629 | beta | 0.5 | 0.6657 | 0.3612 | 0.9511 | beta |
| rho_pif | 0.5 | 0.8048 | 0.7138 | 0.894 | beta | 0.5 | 0.7787 | 0.6866 | 0.8845 | beta | 0.5 | 0.8074 | 0.7238 | 0.8963 | beta | 0.5 | 0.7916 | 0.698 | 0.8811 | beta |
| rho_EYF | 0.5 | 0.65 | 0.3297 | 0.9721 | beta | 0.5 | 0.6446 | 0.3381 | 0.95 | beta | 0.5 | 0.6395 | 0.3364 | 0.9532 | beta | 0.5 | 0.6455 | 0.3464 | 0.9404 | beta |
| rho_Epif | 0.5 | 0.0475 | 0.0002 | 0.0974 | beta | 0.5 | 0.0607 | 0.0001 | 0.1278 | beta | 0.5 | 0.0508 | 0.0001 | 0.1094 | beta | 0.5 | 0.0589 | 0.0003 | 0.1275 | beta |
| rho_ETS | 0.5 | 0.3195 | 0.0122 | 0.6134 | beta | 0.5 | 0.7612 | 0.5431 | 0.9779 | beta | 0.5 | 0.4903 | 0.1209 | 0.8801 | beta | 0.5 | 0.757 | 0.6113 | 0.9244 | beta |
| rho_ELEV | 0.5 | 0.9183 | 0.8104 | 0.9975 | beta | 0.5 | 0.9686 | 0.942 | 0.996 | beta | 0.5 | 0.9623 | 0.932 | 0.9964 | beta | N/A | N/A | N/A | N/A | N/A |
| rho_R | 0.5 | 0.3763 | 0.1653 | 0.5701 | beta | 0.5 | 0.6428 | 0.5533 | 0.7338 | beta | 0.5 | 0.4127 | 0.1557 | 0.6614 | beta | 0.5 | 0.6233 | 0.5089 | 0.7407 | beta |
| mu_pi | 2 | 2.8076 | 2.1712 | 3.4376 | gamm | 2 | 2.583 | 2.0321 | 3.1362 | gamm | 2 | 2.7395 | 2.1467 | 3.3252 | gamm | 2 | 2.8149 | 2.1981 | 3.3887 | gamm |
| mu_Y | 0.5 | 0.055 | 0.0296 | 0.0803 | gamm | 0.5 | 0.0536 | 0.0283 | 0.0772 | gamm | 0.5 | 0.0534 | 0.032 | 0.0763 | gamm | 0.5 | 0.0513 | 0.027 | 0.0754 | gamm |
| rho_Rf | 0.5 | 0.728 | 0.6229 | 0.84 | beta | 0.5 | 0.7331 | 0.6295 | 0.8425 | beta | 0.5 | 0.7336 | 0.6276 | 0.8386 | beta | 0.5 | 0.7356 | 0.621 | 0.846 | beta |
| rho_ERf | 0.5 | 0.7371 | 0.6367 | 0.846 | beta | 0.5 | 0.7347 | 0.6315 | 0.8416 | beta | 0.5 | 0.7301 | 0.6303 | 0.8421 | beta | 0.5 | 0.7278 | 0.6125 | 0.8448 | beta |
| habit | 0.5 | 0.1684 | 0.0646 | 0.273 | beta | 0.5 | 0.3622 | 0.1821 | 0.5346 | beta | 0.5 | 0.1841 | 0.0563 | 0.2947 | beta | 0.5 | 0.2379 | 0.0928 | 0.3805 | beta |
| eta_plus | 0.5 | 0.1591 | 0.0169 | 0.2837 | gamm | 0.5 | 0.7249 | 0.0392 | 1.4156 | gamm | 0.5 | 0.2203 | 0.0253 | 0.4175 | gamm | 0.5 | 0.3779 | 0.0775 | 0.6697 | gamm |
| chi | 0.05 | 0.0267 | 0.0193 | 0.0342 | invg | 0.05 | 0.063 | 0.0528 | 0.0729 | invg | 0.05 | 0.0267 | 0.0196 | 0.0346 | invg | 0.05 | 0.0263 | 0.0185 | 0.0336 | invg |
| psi | 1 | 1.6399 | 0.9004 | 2.4182 | gamm | 1 | 1.4118 | 0.507 | 2.173 | gamm | 1 | 1.6558 | 0.8362 | 2.4681 | gamm | 1 | 2.0657 | 0.9671 | 3.1267 | gamm |
| theta_D | 0.5 | 0.0505 | 0.0004 | 0.1016 | beta | 0.5 | 0.55 | 0.3454 | 0.7634 | beta | 0.5 | 0.1188 | 0.0003 | 0.3534 | beta | 0.5 | 0.3621 | 0.1682 | 0.5448 | beta |
| theta_M | 0.5 | 0.92 | 0.8955 | 0.9452 | beta | 0.5 | 0.9421 | 0.91 | 0.9786 | beta | 0.5 | 0.9285 | 0.8956 | 0.964 | beta | 0.5 | 0.9668 | 0.9489 | 0.9865 | beta |
| iota_D | 0.5 | 0.4847 | 0.0741 | 0.8783 | beta | 0.5 | 0.2866 | 0.006 | 0.598 | beta | 0.5 | 0.5303 | 0.1363 | 0.9199 | beta | 0.5 | 0.4271 | 0.0374 | 0.8045 | beta |
| iota_M | 0.5 | 0.1931 | 0.0351 | 0.3403 | beta | 0.5 | 0.3422 | 0.121 | 0.6681 | beta | 0.5 | 0.2564 | 0.0239 | 0.5436 | beta | 0.5 | 0.4585 | 0.0672 | 0.8203 | beta |
| phi_e | 0.5 | 0.1155 | 0.0131 | 0.2057 | beta | 0.5 | 0.0823 | 0.0002 | 0.1708 | beta | 0.5 | 0.1085 | 0.0088 | 0.1907 | beta | 0.5 | 0.159 | 0.0153 | 0.2951 | beta |
| phi_lambda | 0.001 | 0.0011 | 0.0003 | 0.0021 | invg | 0.001 | 0.0006 | 0.0002 | 0.001 | invg | 0.001 | 0.001 | 0.0003 | 0.0019 | invg | 0.001 | 0.0009 | 0.0002 | 0.0017 | invg |
| phi_f | 2 | 1.6048 | 1.483 | 1.7321 | gamm | 2 | 1.5661 | 1.4377 | 1.6939 | gamm | 2 | 1.5978 | 1.4708 | 1.7221 | gamm | 2 | 1.6434 | 1.5326 | 1.7548 | gamm |
Table 3a: Posterior Estimates of Parameter Means Under Four Model Specifications
The most notable results are for the estimates of elasticity of external finance premium, χ . It turns out that the posterior means for χ are very close under benchmark model, NoFin-Shock model, and eS-only model (0.0267, 0.0263, and 0.0267, respectively), while the posterior mean under eN-only model turns out to be quite different (which is 0.0630). Compared to BGG’s original calibration (which was 0.05) and Christensen and Dib’s (8) estimate (which was 0.042 based on U.S. data), the estimates of χ under benchmark model, NoFin- Shock model, and eS-only model are relatively low. In contrast, under eN-only model, the estimate of turned out to be relatively high. This contrast in the estimates of χ indicates that the estimation result can be sensitive to the specification of the shock structure. Since χ is the key parameter in controlling the financial accelerator effect, this gap in the estimates of χ will make the magnitude of propagation from monetary policy shock quite different, especially for the business fixed investment, as we will see later in the estimated IRF.
Turning to the elasticity of capital goods production, ψ , the posterior means are more or less similar among four models. The posterior mean of NoFin-Shock model turns out to be slightly higher (which is 2.0657) than other three models, but it is not significantly different based on the confidence interval reported. The differences in shock structures do not seem to matter for the estimate of ψ , at least in our estimates.
Next, the estimation results of the standard deviation of the shocks which are reported at the lower panel of Table 3b. In this paper, since the focus is on the financial shocks, we restrict our attention to the aggregate net worth shock and external finance premium shock. Taking a look at the estimates of the standard deviation of the aggregate net worth shock,  , we notice a difference between the benchmark model and the eN-only model. Under benchmark model, the estimate is relatively small (which is 0.0051), while under the eN-only model, the estimate is relatively large (which is 0.0089) and the difference in the estimate seems to be significant based on the confidence interval. In contrast, turning to the estimates of the standard deviation of the external finance premium shock,
, we notice a difference between the benchmark model and the eN-only model. Under benchmark model, the estimate is relatively small (which is 0.0051), while under the eN-only model, the estimate is relatively large (which is 0.0089) and the difference in the estimate seems to be significant based on the confidence interval. In contrast, turning to the estimates of the standard deviation of the external finance premium shock,  , we find the estimates under the benchmark model and the eS-only model to be very close with each other.
, we find the estimates under the benchmark model and the eS-only model to be very close with each other.
| Full Shocks | eN Shock Only | eS Shock Only | No Fin Shock | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prior | Post. | Prior | Prior | Post. | Prior | Prior | Post. | Prior | Prior | Post. | Prior | |||||||||
| Shock | Mean | Mean | 5% Conf. 95% Conf. | 95% Conf | Dist. | Mean | Mean | 5% Conf. | 95% Conf. | Dist. | Mean | Mean | 5% Conf. | 95% Conf. | Dist. | Mean | Mean | 5% Conf. | 95% Conf. | Dist. |
| eA | 0.01 | 0.008 | 0.0068 | 0.0092 | invg | 0.01 | 0.0094 | 0.0073 | 0.0116 | invg | 0.01 | 0.0081 | 0.0068 | 0.0093 | invg | 0.01 | 0.0082 | 0.0068 | 0.0096 | invg |
| eD | 0.01 | 0.0055 | 0.0039 | 0.007 | invg | 0.01 | 0.0111 | 0.0066 | 0.0158 | invg | 0.01 | 0.0057 | 0.0036 | 0.0078 | invg | 0.01 | 0.0075 | 0.0048 | 0.0101 | invg |
| eG | 0.01 | 0.0223 | 0.0179 | 0.0265 | invg | 0.01 | 0.0298 | 0.0253 | 0.0342 | invg | 0.01 | 0.0238 | 0.0173 | 0.0311 | invg | 0.01 | 0.03 | 0.0256 | 0.0344 | invg |
| eK | 0.01 | 0.0118 | 0.0095 | 0.0141 | invg | 0.01 | 0.0124 | 0.0096 | 0.0151 | invg | 0.01 | 0.0116 | 0.0093 | 0.0139 | invg | 0.01 | 0.0103 | 0.008 | 0.0125 | invg |
| eL | 0.001 | 0.0031 | 0.0023 | 0.0038 | invg | 0.001 | 0.0027 | 0.0019 | 0.0035 | invg | 0.001 | 0.003 | 0.0022 | 0.0037 | invg | 0.001 | 0.0025 | 0.0017 | 0.0032 | invg |
| eLV | 0.01 | 0.0083 | 0.0062 | 0.0104 | invg | 0.01 | 0.012 | 0.01 | 0.0141 | invg | 0.01 | 0.0098 | 0.0083 | 0.0112 | invg | N/A | N/A | N/A | N/A | N/A |
| eMC | 0.001 | 0.0098 | 0.0066 | 0.0127 | invg | 0.001 | 0.0014 | 0.0002 | 0.0031 | invg | 0.001 | 0.0082 | 0.0004 | 0.0125 | invg | 0.001 | 0.0011 | 0.0002 | 0.0026 | invg |
| eN | 0.01 | 0.0051 | 0.0028 | 0.0073 | invg | 0.01 | 0.0089 | 0.0071 | 0.0107 | invg | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A |
| ePf | 0.001 | 0.0015 | 0.0013 | 0.0017 | invg | 0.001 | 0.0015 | 0.0013 | 0.0017 | invg | 0.001 | 0.0015 | 0.0013 | 0.0017 | invg | 0.001 | 0.0015 | 0.0013 | 0.0017 | invg |
| eR | 0.001 | 0.0041 | 0.0027 | 0.0052 | invg | 0.001 | 0.0024 | 0.0019 | 0.0029 | invg | 0.001 | 0.0038 | 0.0022 | 0.0053 | invg | 0.001 | 0.0026 | 0.0019 | 0.0033 | invg |
| eRf | 0.001 | 0.0009 | 0.0008 | 0.001 | invg | 0.001 | 0.0009 | 0.0008 | 0.001 | invg | 0.001 | 0.0009 | 0.0008 | 0.001 | invg | 0.001 | 0.0009 | 0.0008 | 0.001 | invg |
| eS | 0.001 | 0.0006 | 0.0005 | 0.0007 | invg | N/A | N/A | N/A | N/A | N/A | 0.001 | 0.0006 | 0.0005 | 0.0007 | invg | N/A | N/A | N/A | N/A | N/A |
| eTS | 0.01 | 0.0092 | 0.0061 | 0.0119 | invg | 0.01 | 0.0164 | 0.0133 | 0.0195 | invg | 0.01 | 0.0164 | 0.0069 | 0.0171 | invg | 0.01 | 0.0161 | 0.0136 | 0.0187 | invg |
| eYf | 0.001 | 0.0049 | 0.0042 | 0.0055 | invg | 0.001 | 0.0049 | 0.0042 | 0.0056 | invg | 0.001 | 0.0049 | 0.0042 | 0.0055 | invg | 0.001 | 0.0049 | 0.0043 | 0.0056 | invg |
Table 3b: Posterior Estimates of Shock Standard Deviations Under Four Model Specifications.
Finally, we now turn to the marginal likelihoods of each model. As can be seen from Table 3a and 3b, the benchmark model has the highest marginal likelihood among three models (we exclude the NoFin-Shock model since we cannot compare it on equal footing). This result is not surprising. Since the benchmark model incorporates both financial shocks, it should have higher flexibility in ‘matching’the model to the observed data compared to the eN-only or eS-only models19. Now, the marginal likelihood of the eN-only model was sizably lower than those of the benchmark model and eS-only model. If we are to take marginal likelihood as a model selection criteria, the financial shock structure only with the aggregate net worth shock may not be appropriate in accounting for the observed data compared to the benchmark model or eS-only model. Also, relatively low marginal likelihood under the eN-only model may, in part, explain why the eN-only model yielded a very different estimate for χ compared to other models.
Estimated IRF
Next, we report the estimated IRF from our four model specifications. Since the dimension of endogenous variables and shocks are large, we restrict our attention to selected shocks and variables. Specifically, for the variables we restrict our attention to the followings; GDP, consumption, business fixed investment, capital price, inflation rate, external finance premium, business credit, net worth, and leverage ratio. For the shocks, we restrict our attention to the followings; aggregate technology shock, intertemporal preference shock, investment-specific technology shock, monetary policy shock, external finance premium shock, and aggregate net worth shock.
Figure 1 reports the estimated IRF of the aggregate technology shock for the four model specifications. As can be seen from the figure, the benchmark model, NoFin-Shock model, and eS-only model have similar magnitudes and patterns of IRF, while the IRF of the eN-only model reveals some difference in magnitude of response although the qualitative patterns are the same. The reason behind this difference is due to the difference in the estimate of χ . The interpretation of the IRFs are as follows. After a positive aggregate technology shock which, in turn, raises the marginal productivity of capital, entrepreneurs will accumulate the net worth above the steady state. Consequently, the leverage ratio decreases and, thus, the external finance premium will decline. Now, since the estimate of χ is larger in the eN-only model, the magnitude of decline in the external finance premium is deeper under the eN-only model compared to other models. This deeper decline in the external finance premium will, in turn, contribute to a larger response in the business fixed investment –i.e., a stronger financial accelerator effect vis-à-vis aggregate technology shock under the eN-only model.
Figure 2 reports the estimated IRFs of the intertemporal preference shock. For this particular shock, all four models have more or less reveal the same magnitudes and patterns of the IRFs. The interpretation of the IRFs are as follows. Given the intertemporal preference shock, consumers become temporarily impatient that they decide to substitute future consumption for current consumption. As a consequence, because of crowding-out effect due to aggregate resource constraint, business fixed investment will fall.
Figure 3 reports the estimated IRF of the investment-specific technology shock. As can be seen from the figure, positive investmentspecific technology shock will lower the cost of producing capital goods, thereby, boosting the business fixed investment. This qualitative pattern is common for all four models, except that the magnitude is slightly different for the NoFin-Shock model due to a difference in the estimate of investment adjustment cost parameter, ψ . Turning to the external finance premium, IRF of the eN-only model reveals a larger increase compared to other models. Again, this is due to a difference in the estimate of χ .
Figure 4 reports the estimated IRF of the monetary policy shock. The magnitude of amplification in IRFs are similar among the benchmark model, NoFin-Shock model, and eS-only model, while the eN-only model reveals larger financial acceleration. The reason behind this difference is obviously attributable to the difference in the estimates of χ . An interpretation is as follow. After a tightening in monetary policy, the aggregate net worth will fall due to higher debt repayment cost, causing the leverage ratio to rise. Consequently, the entrepreneurs will be facing a higher external finance premium. Here, since the elasticity of external finance premium is higher under the eNonly model, the rise in the premium under the eN-only model will be higher compared to other models. As a result, the financial acceleration effect will be stronger and the decline in business fixed investment will be deeper under the eN-only model compared to other models.
Figure 5 reports the estimated IRF of the external finance premium shock. Note that IRFs are only shown for the Full-Shock and eS-only model since external finance premium shock is absent in eN-only or NoFin-Shock by construction. As can be seen from the figure, a positive external finance premium shock raises the cost of financing that the corporate sector reduces the amount of borrowing (or business credit) and, thus, cuts back on the business fixed investment. Further, as a result of prolonged reduction in borrowing, corporate leverage ratio eventually (approximately five quarters after the shock) falls below the initial level. This fall in leverage ratio will contribute to lower the external finance premium, thus partially offsetting the impact from the external finance premium shock. Indeed, business fixed investment starts to recover approximately five quarters after the shock and quickly returns to the initial level.
Figure 6 reports the estimated IRF for a negative aggregate net worth shock. Since aggregate net worth shock is absent in eS-only or NoFin-Shock model, IRFs are only shown for Full-Shock and eN-only model. After a negative net worth shock, the entrepreneur is faced with a need to square the balance sheet equation (9). As a result, the entrepreneur will reduce the capital stock (or reduce the asset side of balance sheet) by reducing the business fixed investment as can be seen from the figure. Now, in order to square the balance sheet, the entrepreneur will increase the borrowing (or increase the liability side of balance sheet) as well. This increase in borrowing will occur because if the entrepreneur tries to square the balance sheet only by reducing the capital stock, then the opportunity cost from forgone investment will be too high. Thus, it is in an interest of the entrepreneur to strike a balance between reduction of asset side and increase in liability side by reducing business fixed investment and by increasing debt. Now, due to an increase in borrowing and decrease in net worth, the leverage ratio will rise. This rise in leverage ratio will contribute to raise the external finance premium, thus prolonging the impact from the aggregate net worth shock. Consequently, it will have a prolonged effect on business fixed investment which is in contrast to the external finance premium shock.
For Figures 5 and 6, one important observation should be made. Turning to the IRF of the external finance premium, it is rising both in Figures 5 and 6. However, turning to the IRF of business credit, it is falling after the shock in Figure 5 and it is rising in Figure 6. Based on this observation, the external finance premium shock can be classified as a ‘supply-side’shock in the credit market and the aggregate net worth shock can be classified as a ‘demand-side’shock in the credit market. Thanks to this qualitatively difference between the external finance premium shock and the aggregate net worth shock, two financial shocks in the model can be identified once the relevant financial data (especially related to external finance premium and business credit) are supplied20.
Variance decomposition
We next consider the forecast-error variance decompositions for selected variables under all four model specifications. For each decomposition, we decompose the variance of forecast-error at the horizon of 1-quarter, 4-quarter, 8-quarter, and 16-quarter. In addition, unconditional variance decomposition of each variable will also be reported.
Table 4 reports the forecast-error variance decomposition based on the benchmark model. Turning to the variance decomposition of GDP, most of the movement in GDP is accounted by aggregate technology shock which is in line with the empirical evidence of the empirical DSGE literature. Financial shocks (aggregate net worth shock and external finance premium shock) accounts for a small portion (1% to 2%) of the movement in GDP. For the business fixed investment, the picture is quite different. As can be seen from the table, the variation of business fixed investment is largely accounted by the investment-specific technology shock, especially on a shorter forecast horizon, while the financial shocks account for non-negligible portion of the variation, especially in a longer horizon. In a longer forecast horizon, the aggregate net worth shock accounts for about 5.6% and the external finance premium shock accounts for about 7.5% of the variation in the business fixed investment. In total, financial shocks accounts for about 13% of the variation in business fixed investment in a longer forecast horizon and this is not a negligible size. Turning to the variance decomposition of the external finance premium, most of the movement is accounted by the external finance premium shock. However, sizable portion of the movement in the external finance premium is attributable to the aggregate net worth shock, especially in a longer forecast horizon. Indeed, the aggregate net worth shock accounts for more than the aggregate technology shock, investmentspecific technology shock, and monetary policy shock in all forecast horizon. Finally, let us turn to the variance decomposition of leverage ratio. Here, recall that we have allowed for a measurement error when observing this variable. With no surprise, large portion of the variation of leverage ratio data is attributed to a measurement error, especially in a shorter forecast horizon. However, it should be also be noted that the share of a measurement error in variance decomposition decreases as the forecast horizon gets longer. For an unconditional forecasterror horizon, measurement error accounts for less than 10% of the movement in leverage ratio data. Aside from a measurement error, it turns out that the aggregate net worth shock is an important shock in accounting for the variation in leverage ratio both in the short and long forecast horizon. The external finance premium shock also turns out to be important, especially in the longer horizon, in accounting for the variation.
| GDP | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eS | eTS | eYf |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 period ahead forecast error (%) | 57.99 | 0.63 | 24.13 | 12.17 | 0.21 | 0 | 1.68 | 0.21 | 0.05 | 0.01 | 0.13 | 0.4 | 0 | 2.39 |
| 4 periods ahead forecast error (%) | 73.01 | 1.66 | 12.92 | 6.5 | 0.1 | 0 | 0.45 | 1.47 | 0.07 | 0.35 | 0.26 | 1.26 | 0 | 1.96 |
| 8 periods ahead forecast error (%) | 79.12 | 1.49 | 8.72 | 3.81 | 0.09 | 0 | 0.99 | 2.04 | 0.05 | 0.66 | 0.24 | 1.64 | 0 | 1.15 |
| 16 periods ahead forecast error (%) | 83.08 | 1.03 | 5.61 | 2.38 | 0.19 | 0 | 1.45 | 2.46 | 0.03 | 0.88 | 0.19 | 2.13 | 0 | 0.56 |
| unconditional forecast error (%) | 93.07 | 0.25 | 1.32 | 0.75 | 0.36 | 0 | 0.67 | 1.52 | 0.01 | 0.52 | 0.03 | 1.41 | 0 | 0.11 |
| Business Fixed Investment | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 9.21 | 2.64 | 0 | 78.28 | 0 | 0 | 5.13 | 1.17 | 0.06 | 0.93 | 0.23 | 2.29 | 0 | 0.05 |
| 4 periods ahead forecast error (%) | 24.94 | 4.03 | 0.02 | 47.77 | 0.07 | 0 | 12.4 | 3.18 | 0.11 | 2.27 | 0.52 | 4.56 | 0 | 0.13 |
| 8 periods ahead forecast error (%) | 36.47 | 3.55 | 0.08 | 27.24 | 1.09 | 0 | 16.3 | 4.82 | 0.12 | 3.14 | 0.72 | 6.29 | 0 | 0.17 |
| 16 periods ahead forecast error (%) | 42 | 2.38 | 0.17 | 17.76 | 3.15 | 0 | 16.4 | 5.81 | 0.11 | 3.4 | 0.76 | 7.88 | 0 | 0.15 |
| unconditional forecast error (%) | 50.83 | 1.7 | 0.26 | 16.72 | 3.75 | 0 | 10.3 | 5.61 | 0.07 | 2.68 | 0.47 | 7.55 | 0 | 0.09 |
| External Finance Premium | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 1.54 | 0.76 | 0.01 | 1.67 | 0.32 | 0 | 1.17 | 5.65 | 0 | 1.7 | 0 | 87.2 | 0 | 0 |
| 4 periods ahead forecast error (%) | 1.75 | 0.75 | 0.04 | 2.88 | 0.81 | 0 | 1.27 | 6.94 | 0 | 2.05 | 0.01 | 83.5 | 0 | 0 |
| 8 periods ahead forecast error (%) | 1.88 | 0.72 | 0.09 | 4.37 | 2.26 | 0 | 1.26 | 8.06 | 0.01 | 2.31 | 0.08 | 79 | 0 | 0.01 |
| 16 periods ahead forecast error (%) | 1.89 | 0.66 | 0.2 | 6.01 | 6.53 | 0 | 1.1 | 9.11 | 0.02 | 2.48 | 0.22 | 71.7 | 0 | 0.02 |
| unconditional forecast error (%) | 1.24 | 0.93 | 0.76 | 6.91 | 21.1 | 0 | 2.13 | 13.3 | 0.03 | 3.77 | 0.32 | 49.5 | 0 | 0.02 |
| Leverage Ratio | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 0 | 0 | 0 | 0 | 0 | 73 | 0 | 27.4 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 periods ahead forecast error (%) | 6.03 | 2.43 | 0.14 | 7.88 | 3.81 | 39 | 4.18 | 24 | 0.03 | 5.88 | 0.2 | 6.13 | 0 | 0.04 |
| 8 periods ahead forecast error (%) | 6.39 | 2.04 | 0.27 | 10.74 | 7.89 | 31 | 3.93 | 22.1 | 0.05 | 5.86 | 0.38 | 9.31 | 0 | 0.06 |
| 16 periods ahead forecast error (%) | 5.49 | 1.5 | 0.42 | 12.27 | 15 | 24 | 2.82 | 19.9 | 0.06 | 5.21 | 0.54 | 13 | 0 | 0.06 |
| unconditional forecast error (%) | 1.7 | 1.28 | 1.03 | 9.43 | 28.8 | 9.7 | 2.91 | 18.7 | 0.04 | 5.14 | 0.43 | 20.8 | 0 | 0.03 |
Table 4: Variance Decomposition under Full-shock Model.
Table 5 reports the forecast-error variance decomposition based on the eN-only model. Let us first turn to the variance decomposition of GDP. In contrast to the benchmark model, sizable portion of the variation in GDP is now accounted by the aggregate net worth shock – as much as 10% in the longer horizon. This is more evident if we turn to the variance decomposition of the business fixed investment. The aggregate net worth shock accounts for more than 10% in the shorter horizon and more than 30% in the longer horizon. Literary taking the result under the eN-only model, the aggregate net worth shock accounts for the variation in the business fixed investment more than the investment-specific technology shock in the longer horizon. Compared to the benchmark model where the investment-specific technology shock accounted for more than the financial shocks, this is a very different result. Turning to the variance decomposition of the external finance premium, astonishingly, majority of the variation is accounted by the aggregate net worth shock in all forecast horizon. Since the aggregate net worth shock is the only financial shock under the eN-only model, perhaps, this restrictive shock structure forced the aggregate net worth shock to account for the variation in the external finance premium. This is one particular example where a difference in shock structure significantly alters the result of variance decomposition. Finally, turning to the variance decomposition of the leverage ratio, the aggregate net worth shock accounts for large portion of the variation. One notable difference compared to the benchmark model is that the share of a measurement error in variance decomposition remains to be large even in the longer forecast horizon which stands in sharp contrast to the benchmark case. This can be considered as evidence that the financial shock structure under the eN-only model is not capable in accounting for the movement in the leverage ratio data appropriately.
| GDP | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eTS | eYf |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 period ahead forecast error (%) | 49.31 | 0.25 | 31.73 | 10.68 | 3.3 | 0 | 0.25 | 0.82 | 0.06 | 1.5 | 0.43 | 0 | 1.68 |
| 4 periods ahead forecast error (%) | 69.69 | 0.7 | 10.74 | 3.69 | 5.1 | 0 | 0.11 | 6.36 | 0.13 | 1.42 | 0.91 | 0 | 1.14 |
| 8 periods ahead forecast error (%) | 74.87 | 0.75 | 6.36 | 2.12 | 4.22 | 0 | 0.09 | 8.51 | 0.09 | 1.58 | 0.75 | 0 | 0.67 |
| 16 periods ahead forecast error (%) | 77.57 | 0.55 | 3.82 | 1.62 | 3.48 | 0 | 0.09 | 10.14 | 0.05 | 1.81 | 0.52 | 0 | 0.35 |
| unconditional forecast error (%) | 80.91 | 0.24 | 2.1 | 1.41 | 2.15 | 0 | 0.09 | 10.75 | 0.03 | 1.92 | 0.22 | 0 | 0.18 |
| Business Fixed Investment | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 15.17 | 3.66 | 0.12 | 64.61 | 0.03 | 0 | 0.52 | 11.35 | 0.04 | 4.17 | 0.26 | 0 | 0.08 |
| 4 periods ahead forecast error (%) | 31.02 | 4.55 | 0.12 | 32.74 | 0.04 | 0 | 0.73 | 23.68 | 0.05 | 6.53 | 0.39 | 0 | 0.15 |
| 8 periods ahead forecast error (%) | 38.45 | 3.46 | 0.17 | 18.12 | 0.16 | 0 | 0.78 | 30.57 | 0.04 | 7.66 | 0.44 | 0 | 0.16 |
| 16 periods ahead forecast error (%) | 40.44 | 2.2 | 0.3 | 13.63 | 0.5 | 0 | 0.75 | 33.62 | 0.04 | 7.92 | 0.47 | 0 | 0.13 |
| unconditional forecast error (%) | 38.82 | 1.94 | 0.39 | 15.65 | 1.7 | 0 | 0.65 | 32.87 | 0.05 | 7.4 | 0.43 | 0 | 0.11 |
| External Finance Premium | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 5.22 | 0.88 | 0.01 | 9.21 | 1.4 | 0 | 0.5 | 70.68 | 0 | 12.06 | 0.01 | 0 | 0.02 |
| 4 periods ahead forecast error (%) | 4.39 | 0.47 | 0.1 | 11.72 | 2.48 | 0 | 0.49 | 68.53 | 0.02 | 11.68 | 0.11 | 0 | 0.01 |
| 8 periods ahead forecast error (%) | 3.83 | 0.29 | 0.28 | 14.11 | 4.51 | 0 | 0.44 | 65.2 | 0.04 | 10.94 | 0.32 | 0 | 0.02 |
| 16 periods ahead forecast error (%) | 3.44 | 0.19 | 0.55 | 15.72 | 9.14 | 0 | 0.37 | 60.05 | 0.07 | 9.8 | 0.62 | 0 | 0.05 |
| unconditional forecast error (%) | 2.19 | 0.15 | 0.78 | 12.54 | 20.13 | 0 | 0.34 | 54.29 | 0.06 | 8.9 | 0.6 | 0 | 0.03 |
| Leverage Ratio | eA | eD | eG | eK | eL | eLV | eMC | eN | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 0 | 0 | 0 | 0 | 0 | 64.51 | 0 | 35.49 | 0 | 0 | 0 | 0 | 0 |
| 4 periods ahead forecast error (%) | 3.08 | 0.44 | 0.09 | 5.84 | 1.45 | 40.27 | 0.27 | 42.16 | 0.01 | 6.25 | 0.11 | 0 | 0.02 |
| 8 periods ahead forecast error (%) | 3.42 | 0.33 | 0.19 | 7.85 | 2.76 | 37.37 | 0.28 | 41.02 | 0.03 | 6.49 | 0.23 | 0 | 0.03 |
| 16 periods ahead forecast error (%) | 3.11 | 0.19 | 0.31 | 9.06 | 5.16 | 37.45 | 0.24 | 38.03 | 0.04 | 6.02 | 0.36 | 0 | 0.03 |
| unconditional forecast error (%) | 1.23 | 0.08 | 0.44 | 7.06 | 11.34 | 42.22 | 0.19 | 32.02 | 0.04 | 5.02 | 0.34 | 0 | 0.02 |
Table 5: Variance Decomposition under eN-only Model.
Table 6 reports the forecast-error variance decomposition based on the eS-only model. For GDP the external finance premium shock accounts for small portion of the variation (1% to 2%). Turning to the business fixed investment, the external finance premium shock accounts for non-negligible size of the variation especially in the longer horizon, although its size is not as large as that of the investmentspecific technology shock. This result under the eS-only model is similar to the result under the benchmark model both qualitatively and quantitatively. Now, turning to the external finance premium, nearly 90% of the variation is accounted by the external finance premium shock for 1-quarter to 16-quarter forecast horizon. Even for unconditional forecast horizon, approximately 60% of the variation is accounted by the shock. Taking this result for a face value, this implies that the exogenous component in eq. (16) is accounting for most of the movement in the external finance premium and the endogenous component in eq. (16) is accounting for only a minor share. Interpreting differently, this result suggest that the eS-only model is not successful in capturing the movement in the external finance premium endogenously and need to rely on the exogenous factor to fit the data. Lastly, turning to the leverage ratio data, a measurement error accounts for most of the variation in the shorter horizon and still a large portion even in the longer horizon. Compared to the benchmark model, the share of a measurement error in variance decomposition is larger both in short and long horizon which indicates a poor performance of the eS-only model in accounting for the variation in leverage ratio data.
| GDP | eA | eD | eG | eK | eL | eLV | eMC | ePf | eR | eRf | eS | eTS | eYf |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 period ahead forecast error (%) | 57.25 | 0.43 | 25.54 | 12.52 | 0.83 | 0 | 0.4 | 0.08 | 0 | 0.23 | 0.45 | 0 | 2.27 |
| 4 periods ahead forecast error (%) | 73.4 | 1.42 | 12.85 | 7.37 | 0.62 | 0 | 0.15 | 0.1 | 0.31 | 0.4 | 1.49 | 0 | 1.88 |
| 8 periods ahead forecast error (%) | 80.4 | 1.29 | 8.44 | 4.56 | 0.42 | 0 | 0.63 | 0.08 | 0.62 | 0.35 | 2.07 | 0 | 1.13 |
| 16 periods ahead forecast error (%) | 84.87 | 0.9 | 5.23 | 2.89 | 0.45 | 0 | 1.06 | 0.05 | 0.85 | 0.26 | 2.89 | 0 | 0.56 |
| unconditional forecast error (%) | 93.01 | 0.24 | 1.34 | 0.99 | 0.45 | 0 | 0.6 | 0.01 | 0.58 | 0.05 | 2.61 | 0 | 0.12 |
| Business Fixed Investment | eA | eD | eG | eK | eL | eLV | eMC | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 9.15 | 2.35 | 0 | 80.35 | 0.03 | 0 | 4.19 | 0.07 | 0.94 | 0.25 | 2.61 | 0 | 0.06 |
| 4 periods ahead forecast error (%) | 24.13 | 3.44 | 0 | 54.25 | 0.15 | 0 | 9.73 | 0.11 | 2.16 | 0.53 | 5.35 | 0 | 0.15 |
| 8 periods ahead forecast error (%) | 36.66 | 3.09 | 0.04 | 33.52 | 1.1 | 0 | 13.49 | 0.12 | 3.11 | 0.73 | 7.95 | 0 | 0.19 |
| 16 periods ahead forecast error (%) | 43.25 | 2.08 | 0.12 | 22.38 | 3.01 | 0 | 14.13 | 0.11 | 3.47 | 0.75 | 10.51 | 0 | 0.17 |
| unconditional forecast error (%) | 49.82 | 1.51 | 0.21 | 20.92 | 3.7 | 0 | 9.09 | 0.08 | 2.82 | 0.49 | 11.25 | 0 | 0.11 |
| External Finance Premium | eA | eD | eG | eK | eL | eLV | eMC | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 1.66 | 0.7 | 0 | 2.19 | 0.27 | 0 | 1.14 | 0 | 1.91 | 0 | 92.12 | 0 | 0 |
| 4 periods ahead forecast error (%) | 1.83 | 0.68 | 0.03 | 3.68 | 0.7 | 0 | 1.22 | 0 | 2.23 | 0.01 | 89.63 | 0 | 0 |
| 8 periods ahead forecast error (%) | 1.92 | 0.62 | 0.08 | 5.51 | 2.04 | 0 | 1.2 | 0.01 | 2.46 | 0.07 | 86.08 | 0 | 0.01 |
| 16 periods ahead forecast error (%) | 1.9 | 0.56 | 0.19 | 7.49 | 5.89 | 0 | 1.03 | 0.02 | 2.58 | 0.21 | 80.1 | 0 | 0.02 |
| unconditional forecast error (%) | 1.3 | 0.82 | 0.72 | 9.11 | 20.48 | 0 | 2.02 | 0.03 | 4.1 | 0.31 | 61.07 | 0 | 0.02 |
| Leverage Ratio | eA | eD | eG | eK | eL | eLV | eMC | ePf | eR | eRf | eS | eTS | eYf |
| 1 period ahead forecast error (%) | 0 | 0 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 periods ahead forecast error (%) | 6.25 | 2.16 | 0.13 | 9.93 | 3.49 | 59.82 | 3.9 | 0.03 | 6.32 | 0.2 | 7.72 | 0 | 0.05 |
| 8 periods ahead forecast error (%) | 6.38 | 1.72 | 0.26 | 13.1 | 7.09 | 49.31 | 3.55 | 0.05 | 6.05 | 0.36 | 12.07 | 0 | 0.06 |
| 16 periods ahead forecast error (%) | 5.2 | 1.18 | 0.39 | 14.27 | 12.74 | 40.99 | 2.44 | 0.06 | 5.08 | 0.48 | 17.1 | 0 | 0.06 |
| unconditional forecast error (%) | 1.48 | 0.93 | 0.81 | 10.3 | 23.17 | 24.21 | 2.28 | 0.04 | 4.64 | 0.35 | 31.76 | 0 | 0.02 |
Table 6: Variance Decomposition under eS-only Model.
Finally, we touch on the variance decomposition result under NoFin-Shock model which is reported in Table 721. For GDP, the share of the investment-specific technology shock in variance decomposition is larger compared to that of the benchmark model, both in short and long horizon. Perhaps the variation in GDP which was accounted by financial shocks under the benchmark model is now picked up by the investment-specific technology shock under the NoFin-Shock model. Turning to the business fixed investment, the variation is largely accounted by the investment-specific technology shock. This result is similar with the empirical DSGE literature which emphasize the importance of the investment-specific technology shock. Now, compared with the benchmark model in this paper, difference in the importance of the investment-specific technology shock is stark especially in the long horizon. Under the benchmark model, the investment-specific technology shock, in the unconditional forecast horizon, accounts for about 17% of the variation in the business fixed investment whereas, under the NoFin-Shock model, it accounts as much as 49% of the variation. Assuming that the benchmark model is the correctly specified model, an omission of the financial shocks will render the model to rely too much on the investment-specific technology shock in accounting for the variation in the business fixed investment, which results into an ‘over-accounting’ by this particular shock. In principle, a question asking which model –the benchmark model, NoFin-Shock model or perhaps other kind of model – is the ‘correct’model is an open question. However, the result reported in Table 7 points for a potential pitfall of ‘over-accounting’by a particular shock, especially when the shock structure is misspecified.
| GDP | eA | eD | eG | eK | eL | eMC | ePf | eR | eRf | eTS | eYf |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 period ahead forecast error (%) | 48.18 | 0.01 | 34.84 | 13.8 | 0.68 | 0.03 | 0.03 | 0.4 | 0.14 | 0 | 1.88 |
| 4 periods ahead forecast error (%) | 68 | 1.09 | 14.64 | 12.25 | 1.43 | 0.01 | 0.09 | 0.33 | 0.48 | 0 | 1.69 |
| 8 periods ahead forecast error (%) | 76.72 | 1.07 | 8.78 | 10.16 | 1.12 | 0.02 | 0.07 | 0.58 | 0.43 | 0 | 1.06 |
| 16 periods ahead forecast error (%) | 84.1 | 0.78 | 4.95 | 7.34 | 1 | 0.04 | 0.05 | 0.88 | 0.32 | 0 | 0.55 |
| unconditional forecast error (%) | 91.9 | 0.27 | 1.93 | 3.21 | 1.19 | 0.05 | 0.02 | 1.15 | 0.1 | 0 | 0.19 |
| Business Fixed Investment | eA | eD | eG | eK | eL | eMC | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 7.14 | 1.68 | 0.09 | 89.78 | 0.01 | 0.13 | 0.03 | 0.95 | 0.14 | 0 | 0.05 |
| 4 periods ahead forecast error (%) | 16.15 | 2.09 | 0.1 | 79.29 | 0.04 | 0.26 | 0.03 | 1.7 | 0.22 | 0 | 0.11 |
| 8 periods ahead forecast error (%) | 27.66 | 2.03 | 0.15 | 66.34 | 0.09 | 0.44 | 0.04 | 2.79 | 0.31 | 0 | 0.16 |
| 16 periods ahead forecast error (%) | 39.65 | 1.6 | 0.26 | 53.18 | 0.2 | 0.62 | 0.04 | 3.9 | 0.37 | 0 | 0.17 |
| unconditional forecast error (%) | 43.31 | 1.24 | 0.34 | 48.57 | 1.57 | 0.53 | 0.04 | 3.97 | 0.32 | 0 | 0.12 |
| External Finance Premium | eA | eD | eG | eK | eL | eMC | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 16.48 | 5.02 | 0 | 48.67 | 4.41 | 0.59 | 0 | 24.76 | 0 | 0 | 0.07 |
| 4 periods ahead forecast error (%) | 12.85 | 3.11 | 0.15 | 55.97 | 6.56 | 0.48 | 0.01 | 20.74 | 0.1 | 0 | 0.02 |
| 8 periods ahead forecast error (%) | 9.57 | 1.84 | 0.48 | 61.01 | 10.26 | 0.35 | 0.04 | 16.02 | 0.39 | 0 | 0.05 |
| 16 periods ahead forecast error (%) | 6.9 | 1.02 | 0.79 | 61.44 | 17.27 | 0.22 | 0.07 | 11.55 | 0.65 | 0 | 0.08 |
| unconditional forecast error (%) | 2.5 | 0.77 | 1.27 | 42.48 | 42.33 | 0.21 | 0.06 | 9.76 | 0.57 | 0 | 0.04 |
| Leverage Ratio | eA | eD | eG | eK | eL | eMC | ePf | eR | eRf | eTS | eYf |
| 1 period ahead forecast error (%) | 14.11 | 3.62 | 0.09 | 53.64 | 5.84 | 0.52 | 0.01 | 22.08 | 0.05 | 0 | 0.03 |
| 4 periods ahead forecast error (%) | 9.51 | 2.1 | 0.38 | 61.11 | 8.73 | 0.38 | 0.03 | 17.44 | 0.29 | 0 | 0.03 |
| 8 periods ahead forecast error (%) | 4.9 | 1.19 | 0.82 | 63.91 | 15.25 | 0.22 | 0.07 | 12.95 | 0.63 | 0 | 0.06 |
| 16 periods ahead forecast error (%) | 2.5 | 0.77 | 1.27 | 42.48 | 42.33 | 0.21 | 0.06 | 9.76 | 0.57 | 0 | 0.04 |
| unconditional forecast error (%) | 1.48 | 0.93 | 0.81 | 10.3 | 23.17 | 2.28 | 0.04 | 4.64 | 0.35 | 0 | 0.02 |
Table 7: Variance Decomposition under NoFinShock Model.
Historical decomposition
Following Smets and Wouters [6,7], we conduct a historical decomposition for selected observed variables: GDP, business fixed investment, external finance premium and leverage ratio. Theoretically speaking, the movement (or deviation from steady state) of any endogenous variable can be ultimately attributed to the movement in exogenous shocks in the model. The aim of the historical decomposition exercise is to account for the historical movement of the endogenous variables by the exogenous shocks from the estimated model. One advantage of the historical decomposition exercise is that it allows us to see the direction and the magnitude22 of contribution of each exogenous shock to the movement of endogenous variables. Keeping this advantage in mind, we now turn to the historical decomposition results under four model specifications.
Figure 7 shows the historical decomposition of four observed variables based on the benchmark model estimation result. The observed data is indicated by a solid line and the contribution of each shock to the historical movement of the data is shown in the form of a bar chart. For GDP historical decomposition, we notice that most of the movement in 1990’s and early 2000’s is accounted by the aggregate technology shock, while the movement in late 2000’s are largely accounted by the country-specific risk premium shock. Notice here that the financial shocks are playing non-negligible role in accounting for the movement, which is consistent with the variance decomposition result reported in Table 4.
Turning to the business fixed investment, we observe that several shocks are contributing to the movement. The aggregate technology shock, investment-specific technology shock, and country-specific risk premium shock are all contributing largely, although the contribution from the investment-specific technology shock is not as large as expected. Now, for the financial shocks, we observe that both shocks (aggregate net worth shock and external finance premium shock) are playing a non-negligible role in accounting for the movement in the business fixed investment. Further, we observe that two shocks account for the movement in opposite direction from time to time. For instance, in the middle of 1990’s, the external finance premium shock contributes positively to the movement of the business fixed investment, while the aggregate net worth shock contributes negatively. But then, in the early 2000’s, both shocks contribute negatively to the movement. The fact that two shocks occasionally contribute in the opposite direction and occasionally contribute in the same direction can be perceived as an evidence that two shocks are well identified in the estimation. It should be kept in mind that when the shocks are not well identified, as we will see later, two shocks are not able to account in opposite direction.
To see the details of how the financial shocks are affecting the movement of business fixed investment, it is useful to look at the historical decompositions of the external finance premium and leverage ratio. First, for the external finance premium, we observe that the external finance premium shock (which enters to equation. (16) exogenously) is contributing for lower premium in the mid 1990’s and contributing for higher premium in the early 2000’s, corresponding to the historical movement in the business fixed investment. Taking a look at the contribution from the aggregate net worth shock, we observe that the shock is contributing to raise the premium from early 1990’s to early 2000’s and then we see reversal of that contribution in the middle of 2000’s. This pattern corresponds with the historical movement in the business fixed investment as well. Second, turning to the leverage ratio, we observe that the aggregate net worth shock (which exogenously enters to the aggregate net worth transition equation (18)) is contributing to raise the leverage ratio throughout early 1990’s to early 2000’s and then contributes to lower the leverage ratio after mid 2000’s. This pattern is basically the same pattern observed in the historical decomposition of the external finance premium.
Figure 8 shows the historical decomposition under the eN-only model. Comparing the historical decomposition results of GDP and the business fixed investment against those under the Full-shock model (Figure 7), we observe that the aggregate net worth shock is taking a larger role under the eN-only model. Indeed, the aggregate net worth shock is one of the main factors in determining the movement of GDP and the business fixed investment under the eN-only, which stands in contrast to the results under the Full-shock model. Further, under the eN-only model, the aggregate net worth shock tends to contribute negatively to the movement in GDP and the business fixed investment from late 1990’s to the middle of 2000’s, but have almost no contribution in the early 1990’s and late 2000’s which stands in contrast to the Full-shock model.
Turning to the historical decomposition results for the external finance premium and the leverage ratio under the eN-only model, we see a deeper mechanism of how the aggregate net worth shock is affecting to the movement of the business fixed investment. Basically, the aggregate net worth shock contributed to raise the premium from late 1990’s to the middle of 2000’s and this rise in the premium corresponds to the rise in the leverage ratio (after smoothing) as we observe in the historical decomposition of the leverage ratio. Indeed, we observe that the historical decomposition pattern of the premium and the leverage ratio to be almost identical under the eN-only model. The reason behind this identical pattern can be attributed to the omission of the external finance premium shock. Without the external finance premium shock, the premium and the leverage ratio are forced to move in tandem (see equation. (15)) resulting to the identical historical decomposition pattern. Not only that, by suppressing the external finance premium shock, the smoothed leverage ratio (not the observed leverage ratio) is forced to move in tandem with the credit spread data as we can see from the figure. Here, we see an example where the error structure of the model (in this case, lack of the external finance premium shock) matters substantially for the accounting of the business cycle.
Figure 9 shows the historical decomposition under the eS-only model. As can be seen, the financial shock (in this case the external finance premium shock) does not play a major role in the historical decomposition of GDP or the business fixed investment. For the business fixed investment, the external finance premium shock plays some role in accounting for the historical movement and the pattern of contribution is similar to that under the Full-shock model, except for the period in the late 2000’s. This difference in the pattern of shock contribution in the late 2000’s can be attributed to the omission of the aggregate net worth shock under the eS-only model.
To see where the difference in the pattern is arising, it is useful to check the historical decomposition of the external finance premium and the leverage ratio data. Let us first focus our attention at the late 2000’s of the historical decomposition result of the external finance premium. Compared to the result under the Full-shock model (Figure 7), we notice that the magnitude of contribution from the external finance premium shock is weaker under the eS-only model especially in 2007 when the sub-prime loan problem broke out. This discrepancy between two models is stemming from the omission of the aggregate net worth shock. Under the Full-shock model, since there is a substantial negative contribution from the aggregate net worth shock, the model is identifying relatively strong effect from the external finance shock to account for the movement in the credit spread. In contrast, under the eS-only model, since there is no contribution from the aggregate net worth shock, the model is identifying relatively weak effect from the external finance premium shock. In retrospect, considering the aftermath of the sub-prime loan problem, the Full-shock model (i.e., the model containing two financial shocks) seems to be accounting for the movement in the credit spread more plausibly. Finally, turning to the historical decomposition result for the leverage ratio data, we observe that the effect from the government expenditure shock is somehow exaggerated under the eS-only model compared to that of Full-shock model. Further, as we see later, the magnitude of a measurement error in leverage ratio is substantial under the eS-only model rendering the gap between the smoothed leverage ratio and observed to leverage ratio to be quite large. Again, these discrepancies can be attributed to the omission of the aggregate net worth shock under the eS-only model.
Smoothed and observed leverage ratio
Here we check how three shock-specifications of the model – i.e., Full-shock model, eN-only model, and eS-only model –are fitting the financial data, in particular the leverage ratio data23. First, let us take a look at Figure 10 which shows the smoothed and observed leverage ratio data under the Full-shock model. As can be seen from the figure, the smoothed leverage ratio under the Full-shock model fits the observed data quite well. This means that the Full-shock model was capable to account for the movement in the observed leverage ratio data without relying too much on a measurement error. Next, let us take a look at Figure 11 which shows the smoothed leverage ratio under the eN-only model. As can be seen from the figure, the smoothed and observed leverage ratio reveal substantial discrepancy with each other. This is largely due to the omission of the external finance premium shock. Without the premium shock, the leverage ratio defined in the model is forced to move in tandem with the credit spread data and this will cause a gap between the smoothed leverage ratio and observed leverage ratio. As a result, the model will largely rely on a measurement error in accounting for this gap. Obviously, reliance on a measurement error is not a convincing way of accounting for the historical movement in the leverage ratio data. Finally, let us turn to Figure 12 which shows the smoothed leverage ratio under the eS-only model. As can be seen, the smoothed and observed leverage ratio reveal considerable discrepancy though not as bad as the case under eN-only model. Qualitatively speaking, the smoothed leverage ratio under the eS-only model does move in the same direction with the historical data most of the time, except for the late 2000’s when the sub-prime loan problem broke out. Quantitatively speaking, however, the gap between the smoothed and observed leverage ratio is considerable. Again, the reason for this considerable discrepancy can be attributed to the omission of the aggregate net worth shock under the eS-only model.
In sum, both the eN-only and the eS-only model revealed a considerable discrepancy between the smoothed and observed leverage ratio, heavily relying on a measurement error in accounting for the movement of the data. Failure of the eN-only and the eS-only model is basically due to the omission of either the external finance premium shock or the aggregate net worth shock. In contrast, we observe that the Full-shock model to have relatively small gap between the smoothed and observed leverage ratio. This means that the Full-shock model did not have to rely on a measurement error in accounting for the movement in the leverage ratio data. This result exemplifies the importance of embedding two financial shocks (external finance premium shock and aggregate net worth shock) into the model in accounting for the movement in financial data. In other words, shock specification does matter in accounting for the movement in financial data.
In section 4, we reported the estimation results of the model with various shock specifications. The estimation results in section 4, however, were based on the fixed data set. In particular, financial data were limited to credit spread data and leverage ratio data. What if the financial data were not confined to credit spread or leverage ratio data? Does the result change substantially from the case where the financial data are fixed? In this section, we explore the estimation results based on the benchmark model (i.e., Full-shock model) by altering the data set.
Why do we need financial data?
We first ask why do we need financial data for estimating the model. What if we do not utilize financial data at all or only utilize limited financial data? In order to answer the question, we take up three versions of data sets where – A) both credit spread data and leverage ratio data are absent, B) credit spread data is utilized, but leverage ratio data is absent, and C) both credit spread data and leverage ratio data are utilized24. We refer to these three versions of data set as version A, version B, and version C, respectively.
Table 8 reports the maximum likelihood estimation (MLE) results regarding the standard deviations of the shocks for each version of data set. In theory, if the shock is well-identified in the estimation, the t-statistics of the standard deviation of the shocks will have high values25. Keeping this in mind, let us see the top panel in Table 8 where the estimation result from version A data set is reported. As can be seen, t-statistics of the standard deviation of the aggregate net worth shock (denoted eN in the table) is not statistically significant. While t-statistics of the standard deviation of the external finance premium shock (denoted eS in the table) is statistically significant, it is not as high as usually reported in the empirical DSGE literature. These low t-statistics may be the sign of ill-identification of the financial shocks under version A data set. Another observation we should note is that t-statistics for all other shocks tend to be low as well. It may be the case that without financial data, the financial shocks are ill-identified and this ill-identification of the financial shocks is ‘contaminating’ the identification of other non-financial shocks. Turning to the middle panel where the estimation result from version B data set is reported, we see that t-statistics for the financial shocks to be higher than those under version A. Also, we observe that t-statistics for other shocks to be substantially higher than those under version A–indeed, the standard deviations of all shocks are statistically significant. Finally, turning to the bottom panel where the estimation result from version C data set is reported, we see even higher t-statistics for the financial shocks compared to version B data set. This is more or less so for other shocks as well. It may be the case that, by utilizing more financial data in the estimation (recall that version B utilizes more financial data than version A and version C more than version B), the financial shocks become more identifiable yielding higher t-statistics and the identification of financial shocks is helping to identify other shocks in the model as well.
| Full Shocks, Version A | Full Shocks, Version B | Full Shocks, Version C | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shock | Prior Mean | Mode | S.D. | t-Stat. | Prior Dist. | Prior Mean | Mode | S.D. | t-Stat. | Prior Dist. | Prior Mean | Mode | S.D. | t-Stat. | Prior Dist. |
| eA | 0.01 | 0.0097 | 0.0084 | 1.1606 | invg | 0.01 | 0.0082 | 0.0009 | 8.8354 | invg | 0.01 | 0.0081 | 0.0009 | 9.1579 | invg |
| eD | 0.01 | 0.007 | 0.0839 | 0.0831 | invg | 0.01 | 0.0067 | 0.0017 | 3.953 | invg | 0.01 | 0.0067 | 0.0016 | 4.2252 | invg |
| eG | 0.01 | 0.0292 | 0.006 | 4.8753 | invg | 0.01 | 0.0297 | 0.0025 | 11.8714 | invg | 0.01 | 0.0297 | 0.0025 | 11.8071 | invg |
| eK | 0.01 | 0.0083 | 0.0128 | 0.6443 | invg | 0.01 | 0.0098 | 0.0012 | 8.1203 | invg | 0.01 | 0.0112 | 0.0014 | 8.2653 | invg |
| eL | 0.001 | 0.0016 | 0.0023 | 0.6818 | invg | 0.001 | 0.0021 | 0.0004 | 4.7524 | invg | 0.001 | 0.0024 | 0.0004 | 5.3686 | invg |
| eLV | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | N/A | 0.01 | 0.0089 | 0.001 | 8.6142 | invg |
| eMC | 0.001 | 0.0018 | 0.0128 | 0.137 | invg | 0.001 | 0.0005 | 0.0001 | 3.442 | invg | 0.001 | 0.0005 | 0.0001 | 3.423 | invg |
| eN | 0.01 | 0.0268 | 0.0161 | 1.6695 | invg | 0.01 | 0.0044 | 0.0017 | 2.5817 | invg | 0.01 | 0.004 | 0.0012 | 3.3325 | invg |
| ePf | 0.001 | 0.0015 | 0.0002 | 8.7842 | invg | 0.001 | 0.0015 | 0.0001 | 12.3061 | invg | 0.001 | 0.0015 | 0.0001 | 12.351 | invg |
| eR | 0.001 | 0.0019 | 0.0007 | 2.8461 | invg | 0.001 | 0.0025 | 0.0004 | 5.8567 | invg | 0.001 | 0.0027 | 0.0005 | 5.8182 | invg |
| eRf | 0.001 | 0.0009 | 0.0001 | 12.328 | invg | 0.001 | 0.0009 | 0.0001 | 13.0422 | invg | 0.001 | 0.0009 | 0.0001 | 13.0453 | invg |
| eS | 0.001 | 0.0005 | 0.0001 | 3.4674 | invg | 0.001 | 0.0006 | 0 | 12.9181 | invg | 0.001 | 0.0006 | 0 | 13.2592 | invg |
| eTS | 0.01 | 0.0156 | 0.0024 | 6.3978 | invg | 0.01 | 0.0158 | 0.0013 | 11.924 | invg | 0.01 | 0.0161 | 0.0014 | 11.7871 | invg |
| eYf | 0.001 | 0.0048 | 0.0004 | 12.1019 | invg | 0.001 | 0.0048 | 0.0004 | 12.154 | invg | 0.001 | 0.0048 | 0.0004 | 12.1736 | invg |
Table 8: MLE results of standard deviations of shocks under various data set.
In order to illustrate the consequences from ill-identification of the financial shocks, we show the historical decomposition of business fixed investment under version A, B, and C. In the top panel of Figure 13, the historical decomposition result under version A data set is shown. We notice that the aggregate net worth shock plays a major role in accounting for the movement in the business fixed investment, while the external finance premium shock plays almost no role. This is in sharp contrast with the historical decomposition result reported in Section 4 under the Full-shock model–the result which is re-posted at the bottom panel of Figure 13 under version C data set – where both financial shocks played a role in accounting for the movement in the business fixed investment. Perhaps the ill-identification of the financial shocks, especially for the external finance premium shock, under version A data set is the culprit behind this odd historical decomposition result. Turning to the middle panel of Figure 13 where the historical decomposition result under version B data set is shown, this time, we notice that the aggregate net worth shock is playing almost no role in accounting for the movement. Again, this is in sharp contrast with the result reported in Section 4 (i.e., version C data set). As we have seen in the MLE result reported in Table 8, the t-statistics of the standard deviations of both financial shocks were statistically significant that there seemed to be no problem regarding the identification of the financial shocks when we, at least, utilized the credit spread data. Yet, we observe this odd historical decomposition result where the aggregate net worth shock is playing almost no role even under version B data set. It may be the case that limited utilization of financial data (recall that version B data set only utilize credit spread for financial data) was not enough to provide sufficient information in identifying the financial shocks.
In sum, when there are multiple financial shocks in the model, it is essential to utilize multiple series of financial data to identify financial shocks in the estimation. As we have illustrated in this section, when no financial data is utilized or if there are insufficient series of financial data, it can be potentially difficult to identify the financial shocks. Further, an ill-identified financial shock may affect the identification of other shocks negatively and can yield misleading historical decomposition result as we have seen in this section. For this reason, in order to identify the financial shocks and to reach a reliable historical decomposition, it is crucial to utilize sufficient series of financial data in the estimation.
Why do we use leverage ratio data?
Next, we ask why we select particular financial data for the estimation, specifically, the leverage ratio data. What if we use some other type of financial data? Here, in order to answer this question, we drop leverage ratio data from the data set and replace it, one after another, with the following financial data; investment deflator, business credit, and stock price index. Thus, three different data sets were created and Full-shock model was re-estimated using three versions of the data set. For each estimation, the investment deflator was matched with the price of capital, qt, business credit data from NBSA was matched with the corporate debt, bt, and, following CMR, the stock price index (TSX) was matched with the corporate net worth, nt, in the model. Following the treatment for the leverage ratio, we allow for a measurement error in each of the observed data.
Figure 14 shows the comparison of smoothed and observed data for the investment deflator, business credit, stock price index, and leverage ratio. The gap between smoothed and observed data represents the magnitude of measurement error. As can be seen from the figures, all three financial data –investment deflator, business credit, and stock price index – reveal a wide gap between smoothed and observed data, heavily relying on measurement error to account for the historical movement. Although we do not report a formal statistics regarding the goodness-of-fit to the observed data, a cursory visual inspection of Figure 14 should be enough to judge that the leverage ratio has the best fit.
There may be several reasons why the financial data considered here revealed a substantial gap between smoothed and observed data. One reason may be that, conceptually, the definition of the variables in the model and the definition of the data may not be consistent with each other. For instance, the stock price may be reflecting the net present value of future profits for firms and may not be compatible with the definition of the corporate net worth prescribed in the model. Indeed, as can be seen from the figure, the observed stock price index tends to be volatile possibly reflecting the forward-lookingness of the variable, while the smoothed variable tend to be more stable perhaps reflecting the nature of net worth being a state variable in the model. Another reason for the gap may arise from the detrending of the observed data. For the estimation here, the investment deflator, business credit, and the stock price index were log-linearly detrended. However, loglinear detrending of the financial data may be inappropriate and some other methods of detrending, possibly non-linear detrending, may be necessary. In contrast, leverage ratio data is a ratio of total asset over net worth that, as long as total asset and net worth are cointegrated, there is no issue of detrending for this data. This can be thought of as another advantage of using leverage ratio data.
Whatever the reason may be, it is clear from Figure 14 that the leverage ratio reveals the best fit to the data among the four financial data considered here. Of course this is not to claim that the leverage ratio has the best fit for any countries or has the best fit under any kind of financial friction model. However, at least for the Canadian case and for the model considered in this paper –i.e., a small-open economy version of BGG model –, leverage ratio data, among other financial data, seems to be a promising candidate to be included in an estimation data set.
In this paper, we have investigated the importance of financial shocks for the Canadian business cycle employing the dynamic stochastic general equilibrium framework à la BGG with an extension of small-open economy feature. In particular, in the spirit of Smets and Wouters and CMR, we explored the importance of the external finance premium shock and the aggregate net worth shock as two financial shocks in the model.
In order to answer the question ‘how important are financial shocks’, it requires caution when choosing the specification of the shock structure. Or to rephrase the statement, we need to validate that both financial shocks – external finance premium shock and aggregate net worth shock – are quantitatively important for the business cycle. As such, we estimated the model under four specifications of financial shocks – 1) the model without financial shocks, 2) the model with only aggregate net worth shock, 3) the model with only external finance premium shock, and 4) the model with both financial shock. It turned out that the specification of the financial shocks matters more or less for the estimation of the parameters and, hence, for the estimated impulse response functions. Further, it turned out that the result of the variance decomposition and historical decomposition can dramatically change depending on which shock specification is adopted. Thus, the shock specification does matter when making inference with the estimation results.
Based on the marginal likelihood statistics and the goodness-of-fit vis-à-vis the financial data, the model with both financial shocks fared better than other shock specifications. In other words, we confirmed that, indeed, both shocks are quite important and none of them are redundant in accounting for the Canadian business cycle. Taking the case of the business fixed investment in Canada, our variance decomposition for unconditional forecast error showed that the external finance premium shock to account for as much as 7.5% and the aggregate net worth shock to account for as much as 5.6% of the variance of the business fixed investment. Combined, the financial shocks accounted for more than 13% of the variance and we regard the size to be non-negligible when accounting for the business cycle.
Before we close the paper, one remark should follow. Former studies in the empirical DSGE liter-ature have emphasized the importance of the investment-specific technology shock in accounting for the movement in the business fixed investment. When we suppressed the financial shocks in our model, we did find the investment-specific technology shock to be important –accounting for 49% of the variance of unconditional forecast error. However, when the financial shocks were present in our model, the relative importance of the investmentspecific technology shock was subdued substantially. Indeed, the shock accounted for only 17% of the variance and the size was not too different from those from the financial shocks combined. Of course, our results are confined to Canadian case and it is too early to judge the importance or unimportance) of the investment-specific technology shock in other countries. Never-the less, our evidence points to a potential importance of the financial shocks in other countries and a re-examination of the role of the investment-specific technology shock in the empirical DSGE literature may be warranted.
The author of this paper would like to thank Ian Christensen, Paul Corrigan, Ippei Fujiwara, Takatoshi Ito, Kazumasa Iwata, Yasuharu Iwata, Takashi Kano, Ryo Kato, Oleksiy Kryvtsov, Cesaire Meh, Rhys Mendes, Masao Ogaki, Yasushi Okada, Giorgio Primiceri, Christopher Sims, Bryan Smith, Daniel Solomon, Nao Sudo, Yaz Terajima, Hajime Tomura, Taka Tsuruga, Koichi Yano, and Yahong Zhang for their valuable comments and discussions. Any remaining errors are the responsibility of the author. The first version of this paper was written when the author was at Bank of Canada. The views expressed in this paper are those of the author and do not necessarily reflect those of Bank of Canada.
1Except for the episode of failures by two small banks – the Canadian Commercial Bank and the Northland Bank, both of them located at the western provinces and heavily invested in oil related sectors – which occurred in September 1985. Due to the economic recession in the early 80’s, which hit the oil related sectors in the western provinces especially hard, two banks eventually defaulted and were pushed out from the financial system. Although some financial ‘contagion’(i.e., eventual acquisitions of the Bank of British Columbia and the Continental Bank of Canada by today’s HSBC Bank Canada) followed after the failures, since the combined asset of two banks was less than 1% of the entire banking industry, the Canadian financial system remained pretty much intact. For more details on the episode of the bank failures in 1985, see Dingle ch.5 [9]. Surprisingly, a bank failure episode in Canada preceding to 1985 goes back as far to the episode of the Home Bank failure in August, 1923.
2For instance, Iacoviello [10], Iacoviello and Neri [11], Christensen et al. [12] among others.
3For empirical DSGE papers with this type of financial friction, see, for instance, Meier and Müller [13], De Graeve [14], Christiano et al. [8], and Christensen and Dib [15]. On a different note, Aoki et al. [16] adopts an external finance premium in modelling residential investment.
4Smets and Wouters [6,7] refer to the external finance premium shock as ‘risk’premium shock or ‘equity’premium shock in their context. In our context, we will refer to this shock as external finance premium shock.
1CMR interprets this stochastic survival rate,  , as reduced form way to capture shocks unrelated to preference or technology in the economy. They name ‘asset price bubble’and ‘irrational exuberance’for such examples.
, as reduced form way to capture shocks unrelated to preference or technology in the economy. They name ‘asset price bubble’and ‘irrational exuberance’for such examples.
6We assume no penalty rate is charged by the financial intermediary.
7To be accurate, GNN incorporates capital utilization in their production function specification. Here, for simplicity, we will assume that capital is fully utilized at any time for any entrepreneur.
8We will elaborate more on this external finance premium when explaining financial intermediary’s behaviour.
9Here, we will exactly follow the results presented by BGG and, thus, will be brief in explaining the behaviour of finanicial intermediary. Interested readers should refer to BGG for more details on optimal contracting problem between entrepreneurs and financial intermediary.
10As analyzed in Covas [20], when production technology is decreasing-return-toscale, leverage ratio will not be equal across the entrepreneurs. In such a case, heterogeneity across the entrepreneurs and distribution of leverage ratio should be explictly taken into account.
11As for notation, aggregate variable is expressed by suppressing the argument j. For instance, variable nt; where argument j is suppressed, stands for aggregate net worth instead of entrepreneur j’s net worth.
12Recently, Dupor, Kitamura, and Tsuruga [24] show that inflation persistence can be motivated by a micro-founded model which integrates sticky price and sticky information.
13To be accurate, Smets and Wouters [6,7] refer to their financial shock as ‘equity premium shock’. However, this shock is essentially the same as external finance premium shock in our model, in the sense that it affects the financing cost of capital goods exogenously.
14To be accurate, CMR refers to this shock as ‘financial wealth shock.’ In our paper, however, noting an importance of this shock to the entrepreneurial aggregate net worth, we will simply refer to this shock as ‘aggregate net worth,’unless otherwise noted.
15The sources of this index are due to Scotia Bank for the period of 1980Q1 to 1999Q3 and Merrill Lynch for the period of 1999Q3 to 2007Q4. Two indices by Scotia Bank and Merrill Lynch were equalized and connected at 1999Q3.
16Dib et al. [19] adopts business prime rate less real interest rate as a proxy for external finance premium. By adopting corporate BBB bond spread in this paper, we believe that we can capture the ‘average’credit spread of the business sector rather than ‘prime’credit spread. Further, credit spread based on business prime rate reveals significant persistence since the late 90’s in Canada, behaving as if it is fixed and independent of the corporate balance sheet. This is another reason why we adopt BBB corporate bond spread as a proxy for the credit spread.
17In our paper, we attempt to eliminate the term premium by demeaning the raw yield spread data where the raw yield spread is simply equal to the overnight rate less 10-year government bond yield. Implicit assumption we make here is that the term premium is stationary during the sample period.
18To be accurate, we did not demean the Canadian inflation, but rather we subtracted 2% (or 0.5 quarterly percentage rate) from the inflation rate series. This is due to the modeling assumption such that the steady state of the moving inflation target, t , is equal to 2%. This assumption is based on the fact that the Bank of Canada has fixed the inflation target at 2% since the end of 1995.
19However, it is worth noting that the marginal likelihood of eSonly model was strikingly close to that of benchmark model.
20Notice that it will be extremely di¢ cult to identify two financial shocks just based on real-side (as opposed to financial-side) data. This is because, by construction, the qualitative pattern of IRFs related to real-side variables will be similar for both financial shocks – i.e., real-side economy and financial-side economy are linked by the external finance premium which is the only real-financial linkage in the model. Indeed, if we take a close look at the IRFs of real-side variables such as GDP, consumption, business fixed investment, captial price and inflation in Figures 5 and 6, we notice that the directions of IRF movements are the same for both financial shocks.
21Here in Table 7, since financial shocks are absent and financial data (i.e., credit spread and leverage ratio data) are not observable in NoFinshock model, the variance decomposition for external finance premium and leverage ratio will not be reported.
22In variance decomposition exercise, we have seen how each shock has contributed to the variance (i.e., second moment) of the endogenous variables. In contrast, historical decomposition exercise allows us to see how each has contributed to the first moment of the endogenous variables.
23Another financial data used for estimation is the credit spread data. However, since we assume that the credit spread data can be observed without measurement errors, by construction, the estimated models have a perfect fit with the observed data. In other words, smoothed credit spread and observed credit spread data matches perfectly.
24Thus, the estimation result under version C will be exactly the same with fullshock model estimation result reported in Section 4. We report the result under version C to facilitate the comparison against version A and B.
25Recall that identification of the parameters in the maximum likelihood estimation is closely linked with the curvature of the likelihood surface around the mode. For instance, ill-identified parameters may have a loose curvature around the mode or the likelihood function may be multi-modal. Well-identified parameters will have uni-modal likelihood function with sharp curvature. Consequently, well-identified parameters will have relatively small standard error and high t-statistics.