International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2016) Volume 7, Issue 4
This paper presents the results of extensive numerical simulations, based on the control volume method, of 2D nanofluid fluid flow around a heated elliptical cylinder with different incidence angle and aspect ratio. The continuity and momentum equations have been numerically solved using a SIMPLE algorithm. Two types of nanofluids consisting of Al2O3 and CuO nanoparticles dispersed separately in base fluids of water and ethylene glycol mixture 60:40 (by mass), were selected to evaluate their effect on the flow over elliptical cylinder, also their superiority over conventional fluids. The thermo-physical parameters of nanofluid have been estimated using the theory of one fluid phase, a contemporary correlations of thermal conductivity and viscosity of nanofluids have been used in this paper, which are functions of particle volumetric concentration as well as temperature. The results of heat transfer characteristics of nanofluid flow over elliptical cylinder reveled clear improvement comparing with the base fluids. This enhancement is more important in flows with different geometry characteristics of the elliptical cylinder. While the aspect ratio and the incidence angle, exert significant influence on the heat transfer characteristics. The obtained results indicate that the use of aspect ratio 0.83 and incidence angle 79.2° lead to the highest amounts of heat transfer inside the tube.
<Keywords: Nanofluid; Fluid flow; Elliptical cylinder; Heat transfer
a: Major axis along the flow [m]
A: atan (θ)
b: Minor axis normal to the flow[m]
cd: Drag coefficient
cp: Specific heat [J/kgK]
d: Diameter [m]
F: Force [N]
h: Heat transfer coefficient[W/m2K]
H: Height of the computation domain [m]
k: Thermal conductivity [W/mK]
Kb: Boltzmann constant, 1.381×10-23 [J/K]
P: Pressure [Pa]
Pr: Prandtl number Pr = μcp/k
Re: Renolds Number Re = ρU∞A/μ
T: Temperature[K]
U: Velocity [m/s]
Xu: Upstream face distance of the cylinder from the inlet [m]
μ: Dynamic viscosity [Kg/m.s]
Ø: Particle volumetric concentration [%]
ρ: Density [Kg/m3]
θ: Incidence angle 0≤ θ ≤90°
ε: Aspect ratio b/a 0 < ε ≤1
d: Downstream
c: Cylinder
∞: Inlet condition
bf: Base fluid
nf: Nanofluid
np: Nanoparticle
u: Upstream
w: Wall
Due to its important and pragmatic significance, much has been written about flow past bluff bodies and heat transfer in conventional fluids like air and water over the last fifty years. This application is encountered in a very wide range of industrial situations including, aseptic processing of food particles, in water and polymer solutions in heat exchanger etc. [1-3]. Indeed too much theoretical and numerical data on the flow around an elliptical cylinder was presented for a wide range of non-dimensional numbers, also a widespread number of similar studies are available on flow around different geometries using conventional fluids [4-8].
Many experimental studies also were carried out, to investigate the characteristics of the flow around one sphere and an equilateral triangle arrangement of three spheres. It was observed that a continuous flow development involving shearing phenomena and the interactions of shedding vortices caused a high rate of fluctuations over the whole flow field, although most of the time-averaged flow patterns were almost symmetric about the two downstream spheres [9,10]. Similarly, Tyagi et al. [11] studied the effect of free-stream turbulence on the sphere wake and they found that the vortex shedding process downstream of the sphere was reduced when large organized motions were suppressed by the free-stream turbulence.
Recently, Turki et al. [12] presented a new numerical study to analyze the unsteady flow field and heat transfer characteristics in a horizontal channel with a built-in heated square cylinder. The results were presented to show the effects of the blockage ratio, the Reynolds and the Richardson numbers on the flow pattern and the heat transfer from the square cylinder. Heat transfer correlation is obtained through forced and mixed convection. Khan et al. [5] have successfully employed the boundary layer approximation of the momentum and energy equations using the Von Karman–Pohlhausen [13] integral method for flow and heat transfer from an elliptical cylinder. Finally, they get good results compared with the experimental data available for the flow and heat transfer from elliptic cylinder, but most of these were in a large range of Reynolds number. Using the spectral-element method Johnson et al. [14] reported the effects of the Reynolds number (30 ≤ Re ≤ 200) and of aspect ratio (0.01 ≤ ε ≤ 1) on the Strouhal number, drag coefficients and on the onset of vortex shedding. They reported that the conditions for the steady flow regime to be relatively insensitive to the value of aspect ratio ε, whereas the span of the other regimes narrows down with a decrease in the value of ε. For (ε<1), the steady regime was reported to end at Re ≈ (35-40) which is comparable to the commonly used value of ~(40-45) for circular and square cylinders. D’Alessio and Dennis [15] tested the vorticity-stream function form of the Navier–Stokes equations in terms of transformed coordinates to enforce the correct decay of vorticity at large distances from the elliptic cylinder. They presented the values of drag and lift coefficients for Re = (5-20) for different inclinations of the elliptic cylinder ranging from 0° to 90°. Subsequently, this flow was revisited by Dennis and Young [16] studied the steady two-dimensional flow past an elliptic cylinder at various inclinations to the oncoming stream by solving the Navier– Stokes equations in the range of the Reynolds number (1 ≤ Re ≤ 40) and for a range of inclinations (0-90°) for one value of the aspect ratio ε =5.
Aside from these wide ranging applications, model studies involving classical fluids like air, water, ethylene glycol mixture and oils are widely used in industrial applications but they are penalized by their limited thermal properties. At this circumstance, the use of nanofluids with higher thermal conductivity can be considered as a promising solution [17-19]. However, in recent years there have been some new efforts to produce a new class of high efficiency heat exchange media, to highlight the effect of nanoparticles during flow past bluff bodies [1-5]. Vahid Etminan-Farooji et al. [8] investigated, the laminar nanofluid flow and heat transfer around a square cylinder. They showed that the heat transfer improvement is more evident in flows with higher Peclet numbers and higher particle volume concentration, while it is readily acknowledged that the particle diameter imposes an adverse effect on the heat transfer characteristics. In addition, it was shown that for any given particle diameter there is an optimum value of particle concentration that results in the highest heat transfer coefficient. Now a voluminous body of knowledge is available on the literature using nanofluids correlations, many models are presented to consider these different effective parameters on the conductive heat transfer of nanofluids and other thermo physical properties such as viscosity [20] thermal conductivity [21,22]. To the best of the authors’ knowledge, no research on nanofluids flow and heat transfer over elliptical cylinder has been documented. This work thus aims to fill this gap in the current literature. In this study, the fluid flow and heat transfer of a mixture of water and EG as well as various types of nanofluids over a heated elliptic cylinder are numerically simulated.
Problem statement and formulation
The system explored in the present work is the unconfined flow of an incompressible fluid around a two-dimensional heated elliptical cylinder, with the aspect ratio ε at temperature Tc. In this system, the elliptical cylinder (block) is placed symmetrically between two adiabatic upper and lower boundaries. The inlet of the tube is maintained at a constant temperature T∞ in addition, the block is exposed to a free stream with uniform velocity U∞ Figure 1. Here the aspect ratio of the cylinder is defined as the ratio of the length of the major axis (a) parallel to the flow to the length of the minor axis (b) perpendicular to the flow. On the wall free symmetrical slip boundaries conditions were used to avoid the ambiguous effects of the presence of the upper and lower boundaries on the flow characteristics [23]. Here the blockage ratio B is equal to the ratio b/H when θ is null and is approximated by B ~ A/H when θ is different to 0. Where A is a function of θ and a, which are respectively the angle of rotation of the elliptical cylinder and the major axis along the flow of the elliptical cylinder along the direction of flow, this fraction normally shouldn’t exceed 0.2. Consequently, depending on the values of θ many simulations have been conducted to examine the impact of the blockage ratio on the ultimate results, a small dependence was discovered when the blockage ratio is around 0.1. Indeed, more the blockage ratio is smaller the faster simulation will be. Moreover, the non-dimensional upstream distance between the channel inlet and the front surface of the elliptical cylinder, Xu/A, is taken around 1 and 2, the non-dimensional downstream distance between the rear surface of the elliptical cylinder and channel outlet, Xd/A, is between 4 and 6. A prudent choice of those parameters is by necessity is a compromise between the computational time (which increase rapidly with increasing H, Xu and Xd) and the extent of boundary effects on the accuracy of the results (which deteriorate with decreasing the values of H, Xu and Xd) [1,8].
Considering the incompressible and steady flow past elliptical cylinder as shown schematically in Figure 1, from the details of the domain and the flow characteristics the governing Equations [1-3] for the flow and heat transfer are written as:
Continuity
(∇⋅U ) = 0 (1)
Momentum

Energy

The physically realistic boundary conditions for this flow are outlined below
• At the surface of the elliptical cylinder, no slip condition is used, the velocities on the surface of the block are considered null.
• The surface of block is assumed to be isothermal at Tc = 350 K.
• At the inlet, uniform axial velocity U∞ and temperature T∞ of the entering fluid are implemented.
• In the present work, for the walls adiabatic free symmetric slip boundary conditions are used.
• At the outlet, the zero diffusion flux is used, and the pressure is chosen without viscous stress.
Numerical solution methodology
The present study was carried out using the control volume method. A first order upwind scheme is used for the convective and diffusive terms and other quantities resulting from the governing equations and the SIMPLE algorithm is employed to solve the coupling between the velocity and pressure fields. For all the simulations performed in this study, the solutions were only considered to be converged when the residuals were lower than 10-6. The two-dimensional, laminar segregated solver was used to solve the incompressible flow on the collocated grid arrangement. The resulting data were then post-processed to obtain the temperature field and convective heat transfer coefficients of the block walls. Certainly, the accuracy and consistency of the numerical results are strongly affected by the choice of the numerical parameters, namely, domain size, grid, time step and convergence criterion, and so on [23,24]. As far as our knowledge, there is no available information on nanofluids flow around an elliptical cylinder thus; the values of aforementioned parameters used when studying the air flow over elliptical cylinder were used as preliminary guesses [1,8].
Grid structure and independence study
In order to study the confining upper and lower boundaries, three blockage ratios of 0.15, 0.1 and 0.05 were tested for different set of concentrations of nanofluid containing nanoparticles of CuO and Al2O3 thus, a monotonic behavior was discovered in the variation of drag coefficient equation therefore, the value of the blockage ration around 0.1 it was found to be adequate to simulate the nanofluid unconfined flow.
At the same time to explore the influence of the upstream distance between the inlet and the front surface of the ellipse and also downstream distance of the cylinder from the outlet, a set of simulations were carried out to check the consistence of parameters, it was found (Xu/A) = 1.5 and (Xd/ A) = 4.5 to be an appropriate values, which are consistent with earlier researches [1,25,26].
To make sure that the obtained results are independent of the size and the number of generated grids. So, several grids with different sizes along the axial, radial and angular directions have been tested for many values of ε and θ; and it has been attempted to consider the best grid, with the highest accuracy and the lowest computation cost. Table 1 shows an ample of grid generation, it is imperative to mention that the element’s size chosen to check the quality of the grid (Normal, fine and finer) has approximately the same average quality even if the geometry change Figure 2. Therefore, computations were carried out by considering adequate domain, subsequently it was indispensable to obtain the size of the domain/grid that upon further increment/ refinement produced negligible changes in the numerical results. In the next fine element size was found to be adequate to simulate the flow of nanofluids around an elliptical cylinder due to its low computational cost and relatively good accuracy.
| Element size | Maximum element size | Minimum element size | Resolution of curvature | θ | ε | Number of elements | Average element quality | Average Growth rate |
|---|---|---|---|---|---|---|---|---|
| Normal | 0.9 | 0.4 | 0.3 | 0 | 0.5 | 4442 | 0.9275 | 1.337 |
| 20 | 0.5 | 4394 | 0.9269 | 1.338 | ||||
| 45 | 0.5 | 4384 | 0.9284 | 1.333 | ||||
| 80 | 0.5 | 4402 | 0.9284 | 1.338 | ||||
| Fine | 0.7 | 0.2 | 0.3 | 0 | 0.5 | 7692 | 0.9274 | 1.335 |
| 20 | 0.5 | 7676 | 0.928 | 1.337 | ||||
| 45 | 0.5 | 7662 | 0.9288 | 1.336 | ||||
| 80 | 0.5 | 7712 | 0.9243 | 1.337 | ||||
| Finer | 0.56 | 0.08 | 0.25 | 0 | 0.5 | 13488 | 0.9274 | 1.339 |
| 20 | 0.5 | 13492 | 0.9285 | 1.34 | ||||
| 45 | 0.5 | 13550 | 0.9296 | 1.335 | ||||
| 80 | 0.5 | 13598 | 0.9281 | 1.337 | ||||
| Normal | 0.9 | 0.4 | 0.3 | 0 | 0 | 4344 | 0.9287 | 1.334 |
| 45 | 0 | 4372 | 0.9301 | 1.337 | ||||
| 80 | 0 | 4378 | 0.932 | 1.325 | ||||
| 0 | 1 | 4454 | 0.9295 | 1.335 | ||||
| Fine | 0.7 | 0.2 | 0.3 | 0 | 0 | 7666 | 0.9248 | 1.338 |
| 45 | 0 | 7746 | 0.9233 | 1.341 | ||||
| 80 | 0 | 7730 | 0.9262 | 1.341 | ||||
| 0 | 1 | 7534 | 0.9295 | 1.333 | ||||
| Finer | 0.56 | 0.08 | 0.25 | 0 | 0 | 13644 | 0.9288 | 1.339 |
| 45 | 0 | 13658 | 0.9279 | 1.34 | ||||
| 80 | 0 | 13632 | 0.9298 | 1.338 | ||||
| 0 | 1 | 11608 | 0.9285 | 1.335 |
Table 1: Effect of element size on the quality of elements.
Nanofluid modeling
In the present the nanofluids are modeled using the one phase fluid model, hence, the thermo-physical properties of nanofluids such as density, specific heat, thermal conductivity and viscosity are calculated based on the relations presented in the literature as listed below:
Density: In the present work, the density of the nanofluids is calculated based on the equation 4 proposed by Pak and Cho [27]:

Specific heat: The specific heat of nanofluids is determined using the equation 5 given by Xuan and Roetzel [28].
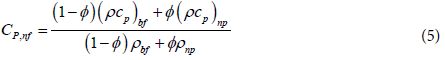
Thermal conductivity: The thermal conductivity is calculated using the model of Koo and Kleinstreuer [21] which takes into account the effect of particle size dnp, particle concentration , temperature T and the properties of the base fluid as well as the effect of the Brownian motion of nanoparticles. Later, Vajjha and Das [29] revised this relation using a broader set of data presented in Table 2. In the following Equation 6,7, the expressions of β for Al2O3 and CuO nanoparticles are given in Table 3.
| Material | ρ(kg/m3) | Cp(J/kgK) | k(W/mK) |
|---|---|---|---|
| Al2O3 | 3970 | 765 | 40 |
| CuO | 6350 | 535.6 | 76.5 |
Table 2: Physical properties of nanoparticles [29].
| Type of particles | β | Concentration |
|---|---|---|
| Al2O3 | 8.4407(100ø)- 1.07304 | 1% ≤ ø ≤ 10% |
| CuO | 9.881(100 ø)-0.9446 | 1% ≤ ø ≤ 6% |
Table 3: Relations proposed by Vajjha and Das for CuO and Al2O3 [29].
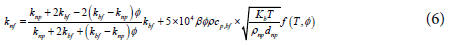
Where
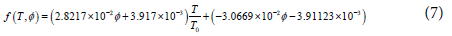
Viscosity: The viscosity of nanofluid was calculated using the recent model of Masoumi et al. [20] based on Brownian motion.

In which:


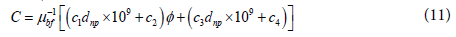
Where:
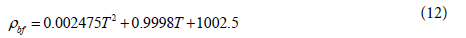
The thermo-physical properties of a mixture of water and EG:W (60:40) were obtained from the ASHRAE Handbook [30]. The values were curve fitted as a function of the temperature with the following Equations 8-12. The properties of nanoparticles and base fluid are taken to be constant during the simulation as mentioned in Table 4.
| Nanofluid | ø | ρ(kg/m3) | Cp(J/kgK) | k(W/mK) | μ(kg/ms) | Pr |
|---|---|---|---|---|---|---|
| EG:Water(60:40) | - | 1079.6 | 3157.4 | 0.357 | 4.53E-03 | 40.033 |
| EG:Water(60:40)/Al2O3 | 2 | 1137.7 | 2989.8 | 0.399 | 4.66E-03 | 34.919 |
| 5 | 1204.1 | 2809 | 0.471 | 4.88E-03 | 29.055 | |
| EG:Water(60:40)/CuO | 2 | 1185 | 2876.4 | 0.419 | 4.68E-03 | 32.149 |
| 5 | 1303.1 | 2637.6 | 0.466 | 4.92E-03 | 27.991 |
Table 4: Physical properties of nanofluids with the base fluid of EG:W (60:40) at T = 300 K.
Thermo-physical properties of EG: W [30]
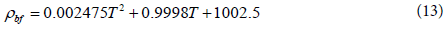

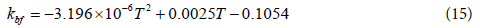
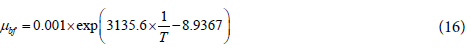
Prior to undertaking the detailed presentation and discussion of the new results obtained in this work, it is imperative to ascertain their reliability and precision. However, before embarking upon the presentation and discussion of the new results, it is desirable to validate the new results on the different elliptical geometry employed in the present work. So, it is worthwhile to validate the choices of numerical parameters and numerical methodology used here. Over the years, reliable numerical and analytic results have been reported in the literature on the values of drag and lift coefficients for steady 2-D flow over elliptical cylinder. The present results was compared with analytic results of Khan et al. [5], Wieselsberger [31] and Van Dyke [32], for a three particular cases circular cylinder (ε = 1), finite plate (ε ≈ 0) and elliptical for the variation of the total drag coefficient with Reynolds number.
The drag and lift coefficients are measures of the forces acting on the elliptical cylinder in the direction of flow (drag) and normal to flow (lift), respectively they are defined in Equations 13-18. From Figure 3 it suffices to say here that the values of elliptical cylinder lie between these two limits and decrease with the Reynolds number. The present results for circular cylinder and finite flat plat are compared with the experimental data of Wieselsberger and Janour [7,31] respectively, from the figure it is clear that the present results are in good agreement with the experimental data. The friction and drag coefficients of the finite flat plate, obtained from the present numerical results are also compared with analytic [5] and experimental values which are closer to those reported by [7] in Figure 4. The both correlations of Van Dyke and Kuo [32,33] further confirm the lend credibility to the reliability of the present numerical simulation for the flow over different geometers used in the present work.


Where FD and FL are the drag and lift forces per unit length of the cylinder, respectively.
In the next level, computations were carried out in a fully laminar regime, choosing fine element size as a grid structure presented in Table 1 and Figure 2. The uniform inlet velocity was adjusted to achieve a constant Reynolds number for each θ and ε, which is chosen to be relatively smaller to don’t reach the turbulent regime. Thus, the quantity (U∞.A) was constant, depending on the geometry used, therefore the corresponding Reynolds numbers would not exceed (50>Re) because the flow becomes unsteady [1,8,14]. During the simulation the temperature of the cylinder was maintained to 350 K, and the temperature of the fluid EG: Water (60:40) was initiated to 270K. The wall is taken isothermal with free symmetric slip conditions are used for artificial confining boundaries Figure 1. The Figure 5 depicts the temperature profile for fixed velocities and different aspect ratio and incidence angle to elucidate the effect of those parameters on the distribution of the temperature inside the tube. From this figure, it appears clearly that temperature vicinity of the cylinder is about 350 K for all the cases, also both the geometry and the incidence angle have an important impact on the distribution of the temperature inside the tube. In the present context, the incidence angle plays a crucial role in the distribution of temperature inside the tube, when the incidence angle θ increase the temperature increases (Figure 5D-5F) and reaches the maximum when θ is near 90°. Likewise, the aspect ratio also affects the temperature distribution inside the tube, thus, the distribution decrease when ε is near 0 (flat plate) and increase gradually to reach the maximum when ε is 1 (circular cylinder). From the last figure it is obvious to underline the enhancement of the temperature inside the tube depending on the geometry and the incidence angle, this indicates the higher temperature gradient and subsequently, greater heat transfer coefficient. It is therefore worthwhile to examine the aspect ratio and incidence angle magnitudes to measure its impact on the heat transfer coefficient. In the following five types of fluids are used in the simulation EG-water (60:40), and nanofluid which is a mixture of EG-water (60:40) and CuO (1%, 5%), Al2O3 (1%, 5%) the choice of those types of nanofluids is governed by the abundance of the physical parameters in the literature and also the correlations to simulate their mixtures as one fluid phase [29].
All the characteristics used in the previous section are maintained in the following simulation; only the thermo-physical parameters related to nanofluids are introduced in the simulation using the above-mentioned Equations (4 -8). Evidently, the heat transfer coefficient is enhanced by the concentration of nanoparticles, also by the kind of the nanoparticles as mentioned in the literature [8,17]. Here, Figure 6 shows the variation of heat transfer coefficient of nanofluid with respect to aspect ratio ε. An increase of aspect ratio results of heat transfer coefficient enhancement, also the heat transfer coefficient increase with the concentration of nanoparticles as well as the kind of nanoparticle used. According to the nature of heat transfer coefficient which is the proportionality constant between the heat flux and the thermodynamic driving force for the flow of heat, this manner proves that for the nanofluids shown in this figure, the upward trend of thermal conductivity dominates the heat transfer coefficient behavior. It can also be seen that the effect of particle concentration becomes more significant at higher aspect ratio.
Extensive, numerical results on the flow over an elliptical cylinder has been studied [4,5,14,16], but, at our knowledge, no study is available for the nanofluids, Figure 7 shows the heat transfer coefficient as a function of the incidence angle θ at an initial temperature of 300K, the aspect ratio is fixed as ε = 0.5. From the figure is clear that the heat transfer coefficient is slightly steady when θ is lower than 20°, then the heat transfer start to grow up until it reaches 76°, and for the incidence angle varying from 76° to 90°, wake enhancement is seen to be delayed as θ grows. At this juncture, it is worthwhile to make an observation, for a given particle concentration the heat transfer coefficient increases significantly at a higher θ. That is due to the fact that for constant thermophysical properties and a fixed geometry the only way to increase the heat transfer coefficient is to increase the inlet velocity, which leads to a higher velocity and temperature gradient near the block. But this could engender a probable uncontrollable turbulence in the flow which is out of the aim of this work.
At the next level, one can gain further insights by examining the effect of the Reynolds number on the heat transfer coefficient. As known Reynolds number presents typical dependence related to the velocity of the flow, thus the heat transfer coefficient will be enhanced by the growth of Reynolds number, since the velocity enhance considerably the flux of temperature. From Figure 8, it is obvious, for a given particle concentration that the heat transfer coefficient increases linearly in different concentrations. To throw more light into the combined effect of the aspect ratio and the incidence angle, the Figure 9 shows the variation of those two parameters with respect to the heat transfer coefficient using nanofluid EG-water (60:40) Al2O3 5%. An examination of this figure depicts the intervals of (θ, ε) where the heat transfer is important. From the yellow cutting line it appears clearly that the maximum is obtained at (79.2°, 0.83). Before leaving this section, it is fair to summarize the current state of the art as fellow; the heat transfer coefficient is enhanced by the concentration of nanoparticles inside the fluid EG-water (60:40) 5% Al2O3 an improvement of 25% of heat transfer coefficient is measured. Furthermore, the aspect ratio ε and incidence angle θ also enhance the heat transfer coefficient by 12%, 4% respectively. Combining those parameters could be useful for real application to enhance the quality of exchanger.
The flow characteristics of the two-dimensional steady flow of incompressible nanofluid fluids over an elliptical cylinder have been investigated numerically. In the present work, two types of nanofluids were used consisting of Al2O3 and CuO nanoparticles with base fluids of water and ethylene glycol mixture 60:40. The thermo-physical parameters of nanofluid have been estimated using the theory of one fluid phase, a contemporary correlations of thermal conductivity and viscosity of nanofluids have been used in this paper, which are functions of particle volumetric concentration as well as temperature. Many numerical investigations have been conducted to secure the accurate mesh and domain size, the blockage ratio B, upstream, downstream and computational domain. The temperature profile for fixed velocities is studied to highlight the distribution of the temperature inside the tube for different aspect ratio and incidence angle. Finally, to put the present results in a context, extensive results on the heat transfer coefficient in terms of nanofluid type, concentration, aspect ratio, incidence angle and Reynolds number are presented and discussed to gain further physical insights into the role of the block shape and nanofluid on the heat transfer inside the tube. The obtained results indicate that the use of aspect ratio 0.83 and incidence angle 79.2° lead to the highest amount of heat transfer inside the tube. The obtained results could be easily applied in a real heat exchanger.