Journal of Geology & Geophysics
Open Access

Griggs Theory of the Viscosity of Rocks: A Chain of Mistakes

William M DeJong^{* *}Correspondence: William M DeJong, Ini-Research, Innovation And Change Inquiry, Delft, The Netherlands, Tel: +31630744341, Email:

Author info »

Introduction

Salt tectonics is a fully developed domain of geology that studies the salt formations on earth [1-6]. Current theory assumes that a plate of rock salt under the compressing stress of a cover of thick layers of earth behaves like a fluid and possesses the intrinsic property of viscosity. Applying this assumed property of rocks, current theory explains the salt pillars (‘diapirs’) of kilometers height that are found on many sites (see for instance Figure 1) as formed by plates of rock salt that have flown slowly upwards during millions of years.

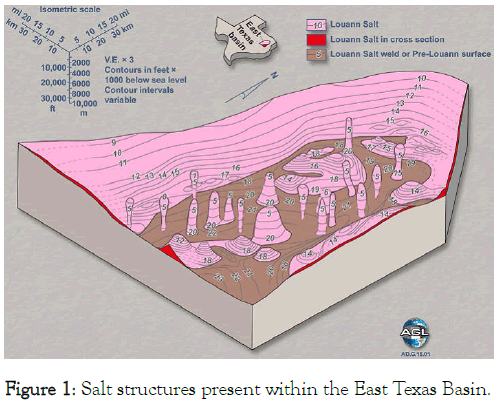
Figure 1: Salt structures present within the East Texas Basin.

In engineering, plates of rock are known for their resistance against high stress and are therefore used as stable building material or underlayment for big, heavy constructions. This engineering knowledge is diametrically opposed to the geological knowledge that large plates of rock under high stress lose their stability and behave like a fluid. The opposed views of engineering and geology on the behavior of rock under stress need examination, as the integrity of empirical science prohibits them to exist side by side.

Firstly, we present the knowledge from engineering on the slow deformation process of pillars of solid material under high, longlasting stress, called ‘creep’ or ‘cold flow’. Subsequently, we assess the theory of David Griggs of the viscosity of rocks, published in 1939, which founds the geological knowledge on the behavior of plates of rock under high stress. We find that Griggs’ theory, which he derived from his experiments with small pillars of rock under high long-lasting stress, consists of a chain of seven mistakes. Finally, we discuss this finding and relate it with: (1) the principles of correct academic research, (2) the investigation, conducted in the 1960-ies, whether caves and corridors in rock salt could be used as safe and stable storage places for nuclear waste; and (3) the computer simulations of the behavior of rock salt, which accurately reproduce the pillars and domes of rock salt found on many sites on earth.

Materials and Methods

Cold flow of a pillar of rock

An important phenomenon in engineering is that a pillar of solid material that is put under the stress of a load initially may seem firm enough to carry that load, but nevertheless collapses after days, months or years. The reason for this is that under high long-lasting stress, a pillar may gradually lose its microstructure and subsequently slowly deforms and finally collapses. This deformation process typically shows three stages [7,8].

In stage 1, the deformation of the pillar is reversible. If the load is removed from the pillar, it retains its original form. In this stage, the pillar is subject to an equilibrating system of forces and is in a state of slight internal relative motion. If the high stress continues, the pillar enters stage 2 of irreversible continuing, linear increasing deformation and is no longer subject to an equilibrating system of forces and enters a state of great internal relative motion. The continuing, linear increasing deformation of the pillar in stage 2 is called ‘creep’ or ‘cold flow’. Finally, the pillar enters stage 3 of complete disintegration; it loses its cohesion and starts to fall apart in pieces (Figure 2).

Figure 2: Deformation of a pillar of rock under a compressing stress.

By trial and error, engineers have learned to prevent creep by making pillars thick enough for the load to be carried, as demonstrated by the pillars of the temple of Apollo on the Acropolis in Greece and the pillars in the Saint Peters church in Rome. In engineering, the possibility of creep of pillars must always be taken into consideration, and be prohibited by choosing materials and dimensions that are fit for the stresses encountered, for instance on a dam in a river [9].

Assessment of Griggs’ theory of the viscosity of rocks

Current theory of the viscosity of rocks rest on the founding paper ‘Creep of rocks’ of David Griggs [10]. In this paper, Griggs reports the results of his experiments with small pillars of rock (for instance lime stone, marble and rock salt) under high longlasting stress. Based on his observations of the phenomenon of creep or cold flow of pillars of rock, Griggs assumes that rock under high stress behaves like a fluid and possesses the intrinsic property of viscosity. In addition, Griggs derives a formula from the Mathematical Theory of Elasticity (MTE) to calculate the assumed viscosity of a plate of rock from measuring the deformation speed of a small pillar of rock under high longlasting stress. We assess Griggs’ theory below in more detail and find it to be a chain of 7 mistakes.

Mistake 1

The assumption without argumentation that a deforming standalone pillar of rock under high stress possesses the intrinsic property of viscosity, which is equivalent to the viscosity of a fluid:

Following the terminology of Michelson [11] when describing the behavior of the surface of the earth and its interior, Griggs [10: p228] denotes stage 1 of the creep process of a pillar of rock under high long-lasting stress as ‘elastic flow’ and stage 2 as ‘pseudo viscous flow’. After this labeling, Griggs [10: p229] assumes that in stage 2 rock possesses the intrinsic property of viscosity, which he denotes as ‘the equivalent viscosity of rock’.For this assumption he provides no arguments. His assumption seems merely based on the presence of the word ‘flow’ in the name ‘cold flow’, respectively ‘pseudo viscous flow’ for stage 2 of the deformation process of a stand-alone pillar of rock under high long-lasting stress.

Mistake 2

The assumption that the mechanical behavior of a stand-alone pillar of rock is identical to the mechanical behavior of a plate of rock:

In addition to mistake 1, Griggs assumes implicitly that the mechanical properties of a stand-alone small pillar of rock are identical to the mechanical properties of a plate of rock. If a stand-alone pillar enters stage 2 of cold flow under a compressive stress P, according to Griggs, also a plate of rock will enter stage 2 of cold flow under the same compressive stress. The mechanical behavior of a stand-alone small pillar of rock under high long-lasting stress, however, differs fundamentally from the mechanical behavior of an identical small pillar that is part of a plate of rock under the same compressive stress, because the surrounding material prevents its lateral deformation. As a consequence, the surrounded pillar will not enter stage 2 of cold flow under the pressure that makes a standalone pillar enter stage 2. (Figure 3). The mechanical behavior of a stand-alone pillar of rock under high long-lasting stress thus is not a valid model for the mechanical behavior of a plate of rock under the same high long-lasting stress.

Figure 3: The mechanical behavior of a stand-alone small cylinder of rock under compressing stress P, compared with its mechanical behavior when embedded in a plate of rock under the same stress.

Mistake 3

The application of the equations of the Mathematical Theory of Elasticity (MTE) under conditions for which the equations do not hold:

Subsequently, Griggs claims that the ‘equivalent viscosity of a rock’ can be calculated from the equations of the Mathematical Theory of Elasticity (MTE), by measuring the speed of cold flow of a small stand-alone pillar of rock. The equations of the MTE, however, describe the state of strain (=fractional deformation) within a solid body “… that is subject to the action of an equilibrating system of forces or is in a state of slight internal relative motion” [12]. The equations of the MTE thus apply to stage 1 of the deformation of a small pillar under stress, but do not apply to stage 2 of irreversible continuing deformation of a pillar of rock under stress in ‘cold flow’. Griggs’ application of the MTE to stage 2 thus is mistaken.

Mistake 4

The calculation of a number from the mistaken application of the MTE and calling that number the ‘equivalent viscosity of a rock, which Griggs labels with the letter η:

Although the MTE is not applicable to stage 2 and any result following from the application of the MTE is mistaken, Griggs derives a formula from the MTE to calculate a number that he calls the ‘equivalent viscosity of a rock’, which he labels with the letter η. By this, he gives his not argumented assumption that rock under pressure behaves like a fluid (see mistake 1) the outlook of the well-established theory of fluid dynamics, where η denotes the intrinsic property of viscosity of a fluid. To prevent confusion, we will denote the ‘equivalent viscosity of a rock according to Griggs’ not as η but as ηG .

Mistake 5

The assumption without argumentation that ηG=tμ:

Griggs assumes [10: p230]: ηG=tμ (t=time and μ =the rigidity of the solid the pillar is made of). For this assumption, Griggs provides no arguments. In addition, his assumption means that the ‘viscosity of a rock according to Griggs’ is time dependent, and thus is not an intrinsic property of a rock. The assumption therefore is invalid.

Mistake 6

Inserting the invalid equation ηG=tμ in the non-applicable equations of the MTE, to derive a formula for calculating the ‘viscosity of a rock according to Griggs’:

Griggs [10: p230] applies the equations of the MTE and Jeffreys' term for elastic

viscous flow (which are not applicable to stage 2 of the creep process) and derives that:

dS/dt= P/3μt (1).

Where:

S=ɛ=CD/L is the fractional cumulative deformation of the pillar, or strain; CD is the cumulative deformation of the pillar and L is the length of the pillar.

P is the compressing stress on the pillar.

μ is the coefficient of rigidity of the solid the pillar is made of.

ηG is the viscosity according to Griggs of the solid the pillar is made of.

Subsequently Griggs [10: p230] applies his invalid assumption (mistake 5):

ηG=μt (2)

From (1) and (2) follows:

ηG=P/(3 dS/dt) (3)

By formula (3), the viscosity of a rock according to Griggs (ηG ) can be calculated easily form the measured speed of deformation of a standalone pillar under high long-lasting stress. As S is a dimensionless number, the dimensions of the viscosity of a solid according to Griggs (ηG) are [Pa.s], which is identical to the dimensions of the viscosity of a fluid (η). This, however, is the only resemblance between the viscosity of a solid according to Griggs and the viscosity of a fluid, which is defined by moving a plate over the surface of a fluid and relating the shear stress τ that the plate encounters, with the gradient of speed within the fluid between the stationary bottom plate and the moving plate at the surface: τ=η ∂u/∂y (Figure 4). The higher the viscosity, the more shear stress is encountered when moving the plate over the fluid [13].

Figure 4: The change of the velocity of a fluid between a moving and a stationary boundary plate.

Mistake 7

The assumption thaηt G is comparable with η and can b e substituted into the equations of fluid dynamics:

As ηG has the same dimensions as the viscosity of a fluid [Pa.s], it can be substituted in the equations of fluid dynamics. This suggests that these equations, which describe the dynamic behavior of a fluid, also hold for plates of rock under the pressure of the overburden of layers of earth that cover them, and that the knowledge on the dynamic behavior of fluids holds as well for plates of rock under the pressure of an overburden. These suggestions are false. Only because of the chain of the mistakes 1 – 6, ηG has identical dimensions as η and can be substituted in the equations of fluid dynamics.

Results

Refinement and extension of Griggs’ experiments

Griggs’ cold-flow experiments with small stand-alone pillars of rock have been repeated by other researchers, under varying conditions of temperature, surrounding pressure and speed of strain. In addition, deformation tests have been conducted with presses that produce a constant strain rate, and measuring the resulting stress on the cylinder for varying strain rates and temperatures [14,15]. The cold flow of a pillar of rock salt appears dependent of the compressing stress, the temperature and humidity present. Advanced research has revealed a broad spectrum of deformation and recrystallisation sub processes: grain boundary migration and sliding, grain rotation, inter granular slip, inter- and intragranular microcracking, grain boundary dissolution-precipitation and dynamic recrystallisation [16,17]. These subprocesses appear to be dependent of the chemical composition of the rock salt, the grain sizes present, the presence of intergranular water, and the magnitude of the stress imposed.

Discussion

Violation of the principles of correct academic research

Griggs theory that a plate of rock salt under the compressing stress of a cover of thick layers of earth, behaves like a fluid and possesses the intrinsic property of viscosity, is based on a chain of mistakes: making not argumented assumptions, applying mathematical equations under conditions for which they do not apply, using a stand-alone pillar under a compressing stress P as a model for a plate under the same compressing stress, postulation of a time dependent intrinsic property, using the well-established label η for the viscosity of fluids to denote an assumed property of rocks. These mistakes are not minor, but each violates one or more principles of correct academic research: carefulness, reliability, honesty, impartiality, responsibility and respect [18].

Caves and corridors in rock salt as safe and stable storage places for nuclear waste

In the 1960-ies, subterranean salt deposits were identified as a promising geologic environment for the disposal of large quantities of heat generating, high-level radioactive waste. Scale model specimens of mine pillars were tested to evaluate the deformation of rock salt under conditions approximating those expected to occur for high-level waste disposal operations in underground excavations.

Lomineck and Bradshaw [19] investigated in 1969 the mechanical behavior of caves and pillars under the stress of the overburden of layers of earth using a model (Figure 5) of a cave and a pillar between its floor and roof Lateral displacement in roof and floor of the model was prevented by a confining metal ring.

Figure 5: Pillar model, cross; derived from Lomineck and Bradshaw.

ɛ=1.30 × 10^-37 T^9.5 σ^3.0 t ^0.30

ἐ=0.39 × 10^-37 T^9.5 σ^3.0 t ^{– 0.70}

Where

ɛ=strain or vertical fractional shortening of pillars (in. /in.) after

2 min of test time (in./in.)

ἐ=strain rate (in. /in. /hr.),

T=absolute temperature (°K)

σ=average pillar stress (psi), and

t=time (hr.).

The model tests and the empirically derived equation for calculation of the strain and strain rate, show a continuing decrease of the strain and strain rate of rock salt and thus a continuing increase of the viscosity of rock salt according to Griggs. These results were confirmed by measurements in mine openings that are up to 12 years old. Lomineck and Bradshaw therefore conclude that subterranean salt deposits are a stable geologic environment for the disposal of large quantities of heat generating, high-level radioactive waste. Their research confirms the well-established engineering knowledge that rock, and in particular rock salt, is a stable material.

Computerized simulations of the mechanical behavior of rock salt:

Based on Griggs’ theory of the viscosity of rocks-which is a chain of mistakes-the equations of fluid dynamics are used to conduct computer simulations of the behavior of hundreds of square kilometers of rock salt under stress, using an extremely high number for the so-called viscosity of a plate of rock salt [20,21].These computer simulations closely reproduce the typical pillar and mushroom structures of the salt formations found on earth. As a plate of rock salt is a stable material under the compressing stress of an overburden of layers of earth, the computer simulations suggest that these salt structures have not been produced by cold flow of rock salt but by hot flow of salt lava, which is the state of matter of salt above 600°C. Salt lava flowing into a fluid with a higher density, will produce the ‘Rayleigh–Taylor instability’ [22] resulting in pillar and mushroom structures.

Conclusion

In engineering, plates of rock are known for their resistance against high stress and are therefore used as stable building material or underlayment for big, heavy constructions. In geology, on the other hand, it is established knowledge that large plates of rock under high stress lose their stability and behave like a fluid. The integrity of empirical science prohibits these opposed views to exist side by side. Therefore, we have assessed the theory of David Griggs on the creep of rocks, which grounds the geological knowledge on the behavior of rocks under stress. Assessment of Griggs' theory reveals that it consists of a chain of seven mistakes, each of them violating one or more principles of correct academic research. Griggs' theory is invalid and must be removed from the domain of science.

References

1. Jackson MPA, SJ Seni. Geometry and evolution of salt structures in a marginal rift basin of the Gulf of Mexico, east Texas. J Geol. 1983;11:131-135.
2. Vendeville BC, Jackson MPA. The rise of diapirs during thin-skinned extension. Mar Pet Geol. 1992;9:331-354.
3. Hudec MR, MPA Jackson. Terra infirma Understanding salt tectonics. Earth Sci Rev. 2007;82:1-28.
4. Urai JL, Schléder Z, Spiers CJ, Kukla PA. Flow and Transport Properties of Salt Rocks, Dynamics of complex intracontinental basins,The Central European Basin System. SpringerVerlag, Berlin Heidelberg. 2008;277-290.
5. Bérest PM, Ghoreychi F, Hadj-Hassen M, Tijani. Mechanical Behaviour of Salt VII,CRC Press, New York. 2012.
6. Jackson MPA, Hudec MR. Salt Tectonics Principles and Practice. Cambridge University Press, Cambridge UK. 2017.
7. Courtney ThH. Mechanical behavior of materials McGraw Hill, Boston. 2000.
8. Bažant ZP, Mija H, Hubler MH, Qiang Yu Q. Damage in Prestressed Concrete Structures due to Creep and Shrinkage of Concrete. In Voyiadjis GZ Handbook of Damage Mechanics, Nano to Macro Scale for Materials and Structures Springer Verlag Berlin. 2015.
9. Zhang Y, Xu W, Shao J, Zhao H, Wang W. Experimental investigation of creep behavior of clastic rock in Xiangjiaba Hydropower Project. Water Sci Eng. 2015;8:55-62.
10. Michelson AA. The Laws of Elastico-Viscous Flow. J Geol. 1920;28:18-24.
11. Love AEH. A Treatise on the Mathematical Theory of Elasticity,Cambridge Press, Cambridge UK. 1920.
12. Schetz JA, Fuhs AE. Fundamentals of Fluid Mechanics. Wiley, New Jersey. 1999.
13. Carter NL, Heard HC. Temperature and rate dependent deformation of halite. Am J Sci. 1970;269:193-249.
14. Zulauf G, Zulauf J, Bornemann O, Brenker FE, Hofer HE, Peinl M, Woodland AB. Experimental deformation of a single-layer anhydrite in halite matrix under bulk constriction, Deformation mechanisms and the role of fluids. J Struct Geol. 2010;32:264–277.
15. Zulauf G, Zulauf J, Bornemann O, Kihm N, Peinl M, Zanella F. Experimental deformation of a single-layer anhydrite in halite matrix under bulk constriction, Geometric and kinematic aspects. J Struct Geol. 2009;31:460–474.
16. Liang W, Zhang C, Gao H, Yang X, Xu S, Zhao Y. Experiments on mechanical properties of salt rocks under cyclic loading. J Rock Mech. Geotech Eng. 2012;4:54-61.
17. Drenth PJD. Responsible conduct in research. Sci Eng Ethics. 2006;12:13–21.
18. Lomenick TF, Bradshaw RL. Model pillar tests for evaluating the structural stability of openings in rock salt utilized for the disposal of radioactive wastes. Nucl Eng Des. 1969;9:269 – 278.
19. Van Keken PE, Spiers CJ, Van den Berg AP, Muyzert EJ. The effective viscosity of rocksalt: implementation of steady-state creep laws in numerical models of salt diapirism. Tectonophysics. 1993;225:457-476.
20. Roberts L, Mellegard K, Hansen F. Mechanical Behaviour of Salt VIII. CRC Press, London. 2015.
21. Andrews MJ, Spalding DB. A simple experiment to investigate two-dimensional mixing by Rayleigh-Taylor instability. Phys Fluids A. 1990;2:922-927.