Journal of Geology & Geophysics
Open Access

Geothermal Exploration by Seismoelectric Survey

Chi Dong^{* *}Correspondence: Chi Dong, Consultent Geologist, Bruno Maldonado, BXM Petroleum Geoscience LLC. Takahiro Kurata, Geothermal Development Inc, Japan, Email:

Author info »

Introduction

In the past decades, researcher have attempted to understand the seismoelectric effect. Conventional seismoelectric methods involve combining elastic seismic wave-induced pressure variations with streaming potential theory (Dong 1990). However, due to the complex nature of this challenge and the rapid horizontal attenuation of the seismoelectric signal (SES), ground detection of this signal is still a difficult task. Based on seismic wave propagation theory, streaming potential equations, and the relation between the seismoelectric signal (SES) and permeability, we derived a 2-dimensional seismoelectric propagation theory. Resulting from this theory and the need to record the seismoelectric signal (SES), we have developed two types of seismoelectric survey instruments (DC-4500 and DC-4800). These seismoelectric instruments have been used to detect aquifers in more than 300 surveys with a 90% success rate. Surveys have also been carried out in petroleum reservoir exploration and achieved success. The maximum penetration depth is up to 4000 meters [1]. Once the seismoelectric signal (SES) is recorded, we apply a statistical estimate method to interpret the seismoelectric data. Our seismoelectric data interpretation has proven to be a 70% match to well log curves. After performing these surveys most cases resulted in the approval of drilling locations.

Materials and Methods

Helmholtz-Smoluchowski Equations: Helmholtz first carried out an experiment with two glasses filled with water and discovered that streaming potential exist at the ends of the tubes at the water/ glass interface. Furthermore, he was able to relate this streaming potential to the fluid pressure gradient (p), dielectric permittivity of liquid (ϵ), zeta potential (ζ), conductivity of fluid (σ), and viscosity of liquid (η). The streaming current is described below by the Helmholtz-Smoluchowski equation:

Where, Estr stands for streaming potential.

According to previous lab experiments can appear, it can be safely assumed that in the seismic frequency range: (1) fluid movement behavior is similar to laminar flow, and (2) water is incompressible. From these assumptions we derived the two- dimensional seismoelectric signal propagation equation (Dong, 2002), which will be described later in this section.

Relation of Seismoelectric Streaming Potential to Permeability: The correlation between streaming potential and permeability has been proposed in theory and proven by experiments. Parkhomenko first gave the relation of streaming potential and permeability in 1971. As shown in Figure 1, streaming potential ζ is to be correlating able to the tube radius in the experiments. In a certain range value of diameter r, when r increases, the streaming potential increase as well (Figure 1).

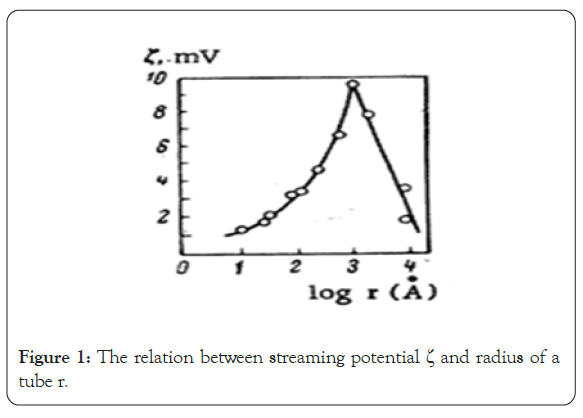
Figure 1. The relation between streaming potential ζ and radius of a tube r.

In subsequent laboratory experiments by Jouniaux Laurence and Jean-Pierre Pozzi (1995) Parkhomenko’s theory of streaming potential and permeability was proven correct. Laurence and Pozzi found that the electrokinetic coupling coefficient is a function of permeability and streaming potential. The details of their work can be found in the Geophysical Research Letters journal (Figure 2).

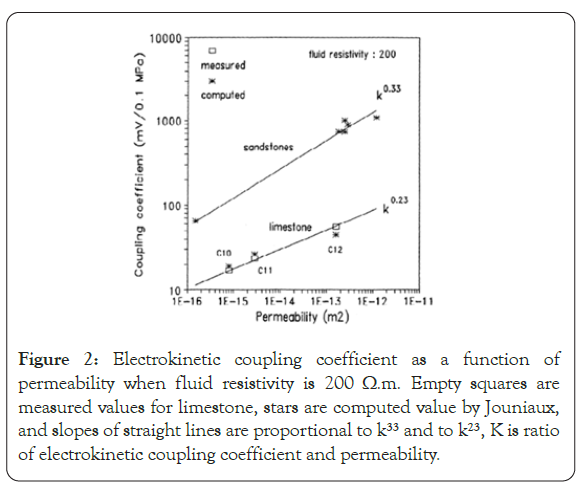
Figure 2. Electrokinetic coupling coefficient as a function of permeability when fluid resistivity is 200 Ω.m. Empty squares are measured values for limestone, stars are computed value by Jouniaux, and slopes of straight lines are proportional to k³³ and to k²³, K is ratio of electrokinetic coupling coefficient and permeability.

We use a schematic to explain the relationship between streaming potential and rock permeability. Two rock samples of the same size have different-sized holes through them. The permeability of sample B with a small-diameter hole (d) is less than the permeability of sample A with a large-diameter hole (D). This is in accordance the physics of permeability definition. Assuming the electronic charge density of the two samples are the same. Note that the circumference of the big hole is larger than the small hole. Therefore, the big hole has more electronic charges. When the rock-fluid interface is disturbed, rock sample A will generate a stronger streaming potential signal (Figure 3).

Seismoelectric Signal Propagation Equations

The streaming potential is measured by placing a pair of electrodes inside the seismic wave field. This occurs as the seismic wave differentially arrives at a pair of electrodes, thus generating a streaming potential. After time zero, as the seismic wave front penetrates into the deep subsurface and reflects to the surface, the seismoelectric signals measured correspond to a seismic response at a specific travel time (reflection at a specific depth in the subsurface) [2]. Applying the Helmholtz equation and expressing the streaming potential in terms of stress in the rock, yields:

E(t)= [ ω2Δρ (p1(t)-p2(t))εζ]/[4πση] (2)

Where,

E(t) is streaming potential, ω is the frequency of the seismic wave,

Δρ is density difference between the rock and the water,

p1 and p2 are rock stresses of the seismic wave at electrodes 1 and 2,

ε is dielectric permittivity of the fluid,

ζ is zeta potential,

η is fluid viscosity, and

σ is fluid conductivity.

Below 2D seismoelectric signal propagation equations in accordance with the stress-strain relation (Voigt's solid formula) can be developed from the Helmholtz equation:

E(x12) is the streaming potential along the x-axis between electrodes 1 and 2,

E(z12) is the streaming potential along the z-axis between the same electrodes,

εxx(e1) is the displacement in the x direction along the x axis at electrode 1,

εxx(e2) is the displacement in the x direction along the x axis at electrode 2,

εzz(e1) is the displacement in the z direction along the z axis at electrode 1,

εzz(e2) is the displacement in the z direction along the z axis at electrode 2.

The partial derivative of fluid displacement with respect to time is included as the same variables used in Equation 1. These equations allow us to analyze a streaming potential signal with respect to travel time of the arriving seismic wave at the pair of electrodes. This arriving seismic wave in turn generates the streaming potential, i.e. seismoelectric signal.

Data Acquisition and Display

From our formulation of the seismoelectric signal propagation, we designed a 1-D observation system composed of two geophones and two pairs of electrodes (See Figure 4). The acquisition pattern is defined by a single seismic point source (buffalo gun or weight drop), two geophones and two electrodes symmetrically placed inline at different offsets from the seismic source.

The DC-4500 system and a military grade computer record the acquisition of the seismoelectric data from both electrodes and geophones. This system has a built-in GPS to record the location of the observation stations.

The seismic and seismoelectric data integration is based on the seismoelectric theory defined by Eq. 3 and Eq. 4. A series of two (2) dimensional profiles permit the building of 3D reservoir models. Our interpretation software facilitates the visualization and analysis of seismoelectric data [3].

Similar to seismic signals, the penetration of seismoelectric signals depends on 3 issues: 1) power of seismic source, 2) attenuation through earth materials, and 3) reflection strength of the target anomaly. Seismoelectric data processing algorithms can increase the resolution and detection of the seismoelectric signal dramatically. Some studies have acquired signals deeper than 4000 meters.

Seismoelectric Survey Principle and Method

Seismoelectric effect is associated with charge activities taking place at the mineral-water interface, defined as the electrical double layer (EDL). When seismic wave passes through porous rocks, it agitates movements of both the rock frame and the pore fluid at different speeds. Relative movement between the fluid and solid particles disturbs the electrical double layer, which in turn produces electric charge. Eventually the variation in electric charge creates an electric potential signal, which can be detected as seismoelectric signals.

The seismoelectric (SES) survey method is a technology based on seismoelectric effect. It receives electric potential signals at ground surface with a seismic source for detecting formation fluid properties. This potential is a function of rock permeability, fluid contents and their saturation.

Superior to the Seismic Reflection method, seismoelectric signals could be screened by proper arrangement of surface probes for vertical transmission. Hence it can reduce the influence of noise from diffraction and out of plane reflection commonly associated with seismic reflection method. Furthermore, since seismoelectric signals are related to fluid properties, the SES method could provide additional information for petrophysical properties of the subsurface formations.

Seismoelectric (SES) signals are sensitive to the permeability of rocks. Therefore, the SES survey has served as a value-adding tool for detecting porous and permeable formations over the last five years for the clients of Seismo Electronics LLC in many countries and regions all over the world [4]. The principle of seismoelectric color strips (SES) for interpretation is shown in the form of. The diagram on the upper half of display shows that different permeability of rock can be recognized by intensities of seismoelectric signal represented by deep green and purple color strips in the lower half of appear. The high permeability rock in the upper-left diagram shows stronger seismoelectric signals. Lower permeability rocks in the middle show medium seismoelectric signals (light green and purple color strips). Dry rock to the right shows very weak signals, or hardly been seen color strips.

The green and purple colors in seismoelectric data are intended to show the fluctuation of seismoelectric signal; this fluctuation is the only information contained in color strips. In other words, the green color layer and purple color layer do not represent different types of lithology or physical properties. If a deep green layer in one measurement point expands to another measurement point which shows a deep purple layer with a similar depth and character, we can determine these signals are generated by the same porous layer because that the change of seismoelectric signal amplitude are the same.

Target Formation Mapping with Seismoelectric Data

Over 300 seismoelectric surveys acquired to date utilized the theoretical approach presented here. The survey objectives were finding water aquifers, geothermal energy, and hydrocarbon reservoirs [5]. For the remainder of this work we will focus on one (1) of the five (5) geothermal projects acquired in the country of Japan. The conclusions and assessments presented are based on the integration of Seismoelectric (SES) data with well log and regional geologic data provided by Geothermal development Japan.

Conclusion

Over the last 83 years private industry and academic researcher have been investigating the seismoelectric theory, but have yet to come up with a fully integrated system to accurately acquire, process and interpret the seismoelectric signal. Until 2014 with the derivation 2D seismoelectric signal propagation equations such a system was developed and the subject of this paper. Our developed acquisition-processing-interpretation system that is based on seismic wave propagation theory, streaming potential equations, and the relation between the seismoelectric signal and relative permeability. Two types of seismoelectric survey instruments, namely DC-4500 and DC-4800, accomplish the acquisition of the seismoelectric signal. The system has been in use since 2007 (2002 patents: US 6,476,608 & International CN 1392420A). In previous studies, the seismoelectric signal has been detected as deep as 4000 meters. The interpretation of the highly permeable zones generating the seismoelectric signal is accomplished by a statistical estimate method. Linear regression methods comparing the seismoelectric signal to SP well log curves have demonstrated a 70% match.

The system is based on 2D seismoelectric signal propagation equations that allow us to analyze a streaming potential signal with respect a delayed travel time of the arriving seismic wave at the surface detection-recording equipment. The delay of the arriving seismic wave at the detection equipment in turn generates the streaming potential, i.e. seismoelectric signal.

The results are displayed using 1-D fluid detection technique that is based on the seismoelectric effect. With proper spatial sampling and well calibration, this method can be extended to 2-dimensional profiles that are much more effective and efficient for direct subsurface fluid detection from a surface location. From these 2-dimensional profiles, we create seismoelectric signature maps at targeted aquifers in order to evaluate the size of the aquifers.

We have presented one (1) case out of over 300 surveys performed. In these surveys, we have achieved a 90% success rate in finding water, hydrothermal and hydrocarbon aquifers (indirect detection).

Acknowledgement

The authors wish to thank Gorge Keller and J. E. White for suggestions for his guidance on this technology. Mr. Qing Wang worked on the seismic interpretation work. In addition, Mr. Jian Zhou for his edits work.

References

1. Gregory AR, Meriwether J. Engineering parameters used in geopressured geothermal Fairway evaluation and test-well site location, Frio formation, Texas Gulf Coast. 1997;4(4):316-320.
2. Dong C. Combining seismic waves with seismoelectrics to perform prospecting and measurements. United States patent 2002.
3. Shore BW. Coherence and transient nonlinearity in laser probing. Spectrochimica Acta Part B: Atomic Spectroscopy. 2003;58(6):969-998.
4. Neev J. Electrokinetic phenomena in fluid saturated porous media (Doctoral dissertation, Colorado School of Mines).
5. Jouniaux L, Pozzi JP. Permeability dependence of streaming potential in rocks for various fluid conductivities. Geophysical Research Letters. 1995;22(4):485-488.
6. Thompson AH, Gist GA. Geophysical applications of electrokinetic conversion. The leading edge. 1993 (12):1169-73.
7. Nanayama F, Kanamatsu T, Fujiwara Y. Sedimentary petrology and paleotectonic analysis of the arc—arc junction: the Paleocene Nakanogawa Group in the Hidaka Belt, central Hokkaido, Japan. Palaeogeogr Palaeoclimatol Palaeoecol. 1993;105(1-2):53-69.
8. Nanayama F, Kanamatsu T, Fujiwara Y. Sedimentary petrology and paleotectonic analysis of the arc—arc junction: the Paleocene Nakanogawa Group in the Hidaka Belt, central Hokkaido, Japan. Palaeogeogr Palaeoclimatol Palaeoecol. 1993;105(12):53-69.
9. Satoh H, Nishida Y, Ogawa Y, Takada M, Uyeshima M. Crust and upper mantle resistivity structure in the southwestern end of the Kuril Arc as revealed by the joint analysis of conventional MT and network MT data. Earth, planets and space. 2001;53(8):829-842.
10. Ichihara H, Mogi T, Yamaya Y. Three-dimensional resistivity modelling of a seismogenic area in an oblique subduction zone in the western Kurile arc: constraints from anomalous magnetotelluric phases. Tectonophysics. 2013;603:114-122.