International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Original Article - (2018) Volume 9, Issue 4
Phenomenon of forward slip during the rod rolling occurs due to the fact that roller and rod are moved. Over forward slip causes elongation and often compaction in the rod and also failure in the end manufacture of the rod. In this investigation, by employing finite element method, a three-dimensional simulation is performed on the No-Twist mill process in the rod rolling. Some notable points such as the geometry extraction of rolling line of end product, rod velocity during rolling, neutral angle, height on neutral plane, and forward slip in No-twist mills are studied. Furthermore, an investigation of influential parameters such as coefficient friction between the roller and the rod, initial velocity, initial rod temperature, and the roller rotation velocity on the forward slip are carried out. Eventually, the contour of stress and temperature distribution during the rod as well as in rolling path is studied. Moreover, in order to obtain the mechanical properties of desired steel, the standard models of hot tensile experiment are performed. In addition, in order to attain the different strain rates, a simple tensile experiment are performed. It can be concluded that as the strain rate increases, the yield point and the ultimate tensile strength point increases and decreases, respectively. Moreover, the modulus of elasticity decreases by increasing the temperature. In addition, three-dimensional simulation of rod rolling in No-Twist mill process, a discussion on the simulation results, and computation of forward slip and other parameters were done by ABAQUS/Explicit v.6.14 software.
Keywords: Finite elements method; Forward slip; No-twist mills; Hot rolling; Neural network
It is evident that while the work piece is entering the rollers, has less velocity than peripheral velocity of the rollers, however when it is exiting, it has more velocity than that of the rollers peripheral. Therefore, due to the fact that entering and exiting velocities are not equal, there must be a space in rollers to make the velocity of work piece and horizontal components equal. This area is called neutral line or plane. The entering and existing velocity is denoted by V1 and W2, respectively. Since the section velocity and horizontal component of peripheral velocity are equal only in neutral plane, therefore, a slip can occur in section and roller or in any other points. In exiting plane the section velocity is more than the peripheral velocity of rollers. The velocity inequality is called forward slip.
No-twist mills
There have been a jump in the final rolling mills since 1962 and the first sample was installed in 1966. These machines use rollers with smaller diameter and each of their axes goes around each other about 90˚ and the whole set is adapted horizontally on angle of 45º. Smallwork rolls with approximately diameter of 8 in provide more decrease in cutting levels without increasing their width. Each roller has a groove and therefore there is no need for a setting in these machines. Thus, not only is not the required time for setting the roller wasted, which is done in the ordinary mills, but also it allows the rest of equipment to be set in the central line of the rollers. In order to reducing the level of flatness and carefully acquiring higher dimension, work rolls are usually made of Tungsten Carbide, which its modulus of elasticity is more than that for steel and also possesses higher erosion resistance. Consequently, hard material strips such as rust-proof steel alloy, titanium alloy, nickel, and steel alloy can be manufactured through rolling.
Forward slip studies
Studies which are performed on forward slip are divided into three categories:
1. Studies through which other parameters of the rolling such as the flatness of the roller’s surface, lubrication, and rollers velocity in forward slip are considered. Azizi et al. studied the effect of friction or the amount of upside and downside surface of rollers flatness, pre-tensile, and post-tensile forces on the process quantities such as the force given to the rollers, as well as enough torque for the formation and pressure in the rollers [1]. It was observed that as the friction coefficient increases, the maximum rolling pressure increases, which is certainly undesirable and causes defects like rollers flatness and eventually brings about a poor process of production. Basti et al. made a Temp-disp. coupled and three-dimension finite element model for analyzing the rolling process [2] Xian et al. studied the rolling strip based on MAS rolling process and presented mathematical forward and backward slip models at the beginning as well as the end of strip [3] computation analysis of temperature distribution, anticipating the rolling force and torque, analyzing of fishing tail in rolling process have been done by different researchers [4-11].
2. Researches which are carried out in order to measure the relative velocity and forward slip. For instance, Li et al. studied the model of laser Doppler Velocimetry (LDV), which is a new way of determining the small relative velocity between the strip and roller in the cold rolling [12].
3. Simulation of rolling process by FEM which has been carried out in some researches. Young-gang et al. introduced the energy principle and upper-bound principle methods to solve forceenergy parameters [13]. The fault between the theory and test model does not exceed 15%. Rezai et al. considered an Elasto- Visco plastic problem [14]. In addition, Temp-disp. and explicit have been chosen as the type of dynamic solutions. Jiang et al. employed the 3-dimensional rigid plastic FEM for rolling simulation of thin strips [15]. By doing so, they calculated the modification of level of friction in the rollers entrance. Jiang and Tieu studied the cog height in hot rolling of cog strips [16]. Lenard and Liu et al. proved that in bite rollers the friction will alter, Lenard showed that friction coefficient also changes as a decreasing stream [17-19] Changes add friction to rolling power and model precision.
Hot tensile test
For being cognizant of the mechanical property of input rod in the mill process and using it in the input of ABAQUS/Explicit software, a few hot tensile tests have been carried out. These tests have invaluable numerical significance and this is due to the fact that for the employed steel and for the particular conditions of test which is done in high temperatures, the adequate data for simulation and other utilizations is not available. Furthermore, there has been a thorough study on the data which is provided from a test by MATLAB software. Moreover, several codes, charts, and tables have been achieved which can be used for any other conditions. Neural networks are used for curve fitting and stress versus strain diagram is obtained. Results which are attained in this part represent good comparison with models and references. The entering rod of mill is made of RSt34-2 steel whose chemical element percentage was achieved according to key to steel [20]. The more the Carbon percentage gets, the less the level of steel resistance gets. Conversely as the carbon percentage rises, the steel would be far softer [21].
Make of hot tensile test specimens and performing the hot tensile test
Standard characteristics of tested examples are chosen as ASTM E8M [22]. These tests for three temperatures, namely 900, 950 and 1000 degrees of centigrade and each of them with strain rates of 200, 350 and 500 mm per minute, were done. The first results of the test were saved as a raw data. Moreover, the true as well as the engineering stress and strain were calculated by MATLAB. Consequently, there were codification in the calculation of stress, strain, modulus of elasticity, and yield stress. Eventually, engineering as well as true stress and strain diagrams were drawn by MATLAB.
Figures 1 and 2 given in the following are the results of MATLAB which are drawn for a better comprehension of stress-strain diagram in different temperatures and strain rate. Figure 1 shows the true stressstrain diagram for rates of 200, 350 and 500 mm/min in a temperature of 900ºC. Figure 2 shows the true stress-strain diagram for temperature of 900, 950 and 1000ºC in a strain rate of 500 mm/min.
Calculation of modulus of elasticity
It is important to mention that obtaining modulus of elasticity through stress-strain diagram by conducting the hot tensile test is impossible. Due to the fact that the test has been done in high temperatures and it is highly unlikely to install gage in order to measuring the modulus of elasticity. Furthermore, the elastic property of jaws also causes a mistake in measuring the modulus of elasticity by the diagram. Therefore, data which are related to references are used for acquiring modulus of elasticity due to the lack of developed measuring tools and equipment justifiers. It must be mentioned that the modulus of elasticity is only dependent on temperature. Furthermore, it is crucial to mentioned that the stress-strain curve is the same for each material [23]. With respect to the table of resistant steel, the value of yield stress is 13.8 MPa for the temperature of 940ºC which is related to the strain rate of 0.2 mm/min. Thus, by using the multi-statement curve fitting of No. 5, the magnitudes of modulus of elasticity for temperatures of higher than 940ºC are those which are presented in Table 1. Moreover, the general levels of modulus of elasticity in different temperatures are those presented in Table 2, which demonstrates that the obtained results are not against expectation of curve fitting and can be a precise prediction of modulus of elasticity for the high temperatures. Further details can be found in [22]. Since the yield point, and stress-strain curve depends on the strain rate, the higher the strain rate are, the more the steel goes through a hardening In addition, the resistance of steel raises against fatigue. On the other hand, as the strain rate increases, the elastic properties decrease, and therefore the steel becomes crisper. As a result, when the strain rate becomes more than 200, 350 and 500 mm/min, it is expected that the amounts related to yield point decreases drastically and the steel has had plastic property since the very beginning, particularly the test is done in high temperatures.
| Temperature (°C) | Room Temperature (°C) | 900°C | 930°C | 950°C | 980°C | 1000°C |
|---|---|---|---|---|---|---|
| Modulus of Elasticity (GPa) | 205 | 37.65 | 27.89 | 22.89 | 18.31 | 17.67 |
Table 1: The values of modulus of elasticity for different temperatures by using multi-statement Equation (5), curve fitting.
| Material | Modulus of Elasticity (GPa) | ||||
|---|---|---|---|---|---|
| Room Temperature (°C) | 250°C | 425°C | 540°C | 650°C | |
| Carbon Steel | 207 | 186 | 155 | 134 | 124 |
| Austenitic Stainless Steel | 193 | 176 | 159 | 155 | 145 |
| Titanium Alloys | 114 | 96.5 | 74 | 70 | - |
| Aluminum Alloys | 72 | 65.5 | 54 | - | - |
Table 2: General levels of modulus of elasticity in different temperatures.
Using neural network to estimate the relationship between true stress and true strain
Regarding the presented data of ASM for metals, the plastic behaviors of steels for strain rate of 10-1000 1/s and for the temperature range of 800 ºC -1100ºC, can be expressed as Equation (1).
σ = K + Blog ε (1)
In addition, for plastic behaviors of low carbon steels and for the temperature range of 30ºC -1100ºC, the plastic stress-strain relation can be expressed as;
σ = Kεnσ = Kεn (2)
Where, 0 ≤ n ≤ 1and the value of zero is for a completely plastic material, whereas the value of n=1 is for an elastic material. For customary metals, the values of n are altered from 0.1 to 0.5.
n and k for some metals at room temperature are represented in Mechanical Metallurgy [21].
By using MATLAB, the required code in neural network was developed and the input matrix had a number of data from the plastic area with temperature’s arrays, strain and strain rate. This matrix along with target matrix was defined for MATLAB which included corresponding data of true stress. The employed network consists of three layers in which the number of neurons obtained by using the method of trying and mistake, and ten numbers in two layers are chosen. Furthermore, the “traingda” algorithm was also used for training the network. This algorithm presented far better results than any other algorithms. While using the instruction of “triangda”, the BP method is utilized with variable learning rate and consequently the errors decrease and much more optimum results attained. Overall, an increase in the number of neurons does not necessarily because a better approximation of function, however, an increase in training stages brings about a more ideal approximation of function. Finally, the network is tested and the output is used for the range of temperature data and also for the higher strain rate. Figure 3 depicts the level of adaptation of neural network used for input data for both before and after training. In these figures, the blue lines demonstrate neural network simulation and the green circles demonstrate input data matrix. The stable R which states this adaptation illustrates an acceptable value. Accordingly, the trained neural network can be reliable and can be utilized for data temperature area and higher strain rates.
Analytical procedure
The velocity inequality and work piece velocity on the neutral plane is as follows:
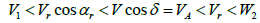 (3)
(3)
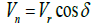 (4)
(4)
Vn : Work piece velocity on the neutral plane
Vr : Peripheral velocity of rollers
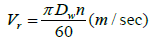 (5)
(5)
Dw : Diameter of work rolls
n : Velocity of rollers (rpm)
Forward slip, which is a result of exiting and peripheral velocity, is defined as that of Equation (6)
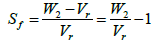
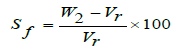 (6)
(6)
Where, 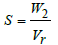 is called the forward slip coefficient.
is called the forward slip coefficient.
Therefore, the velocity of work piece is the summation of whole roller velocity and steel flow velocity. In addition, the work piece moves in the direction of exiting layer. Providing that the work piece has breadth in the length of the roller, forward and backward slip do not occur. The movement velocity of the first pass rollers is gained as 138.4 rad/s and the movement velocity of the second pass rollers is gained as 170.2 rad/s. regarding the velocity inequality, the exiting velocity, and the neutral angle, the rod velocity is taken as the entering velocity. Thus, the work piece velocity while entering the space between the rollers is as follows:
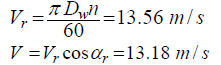
In the relations of yield criterion and plasticity, it is presumed that the behavior of material is elastic-ideally plastic. For hot deformation and for the case of high strain rate, the corresponding metal may illustrate hard working behavior. For metals without hard working, yield stress becomes constant by increasing strain. Nevertheless, for metals with hard working yield stress is depended on the material strain. Furthermore, by increasing the strain of material, yield stress increases. Thus, for these types of metal plastic stress or the equivalent stress or effective stress is implemented. Moreover, in the condition of hot work, yield stress of material is intensely dependent on strain rate. For average strain rate, the following relations can be utilized [22];
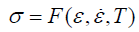
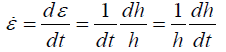 (7)
(7)
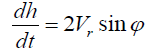 (8)
(8)
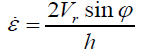 (9)
(9)
First method
The first method of calculation of average strain rate in hot rolling is presented in this section. In this procedure in the deformation zone, the integral of functions is performed with respect to the variable X.
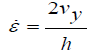 (10)
(10)
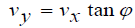 (11)
(11)
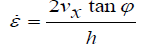 (12)
(12)
By employing the rule of constant volume, it can be conthat:
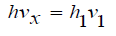 (13)
(13)
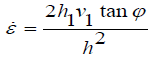 (14)
(14)
By integration with respect to the length which is in contact between roller and work piece, average strain rate can be expressed as;
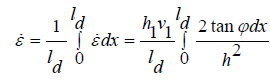 (15)
(15)
2 tanϕ dx = dh (16)
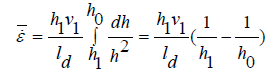 (17)
(17)
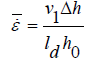 (18)
(18)
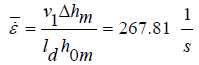 (19)
(19)
For a case with low value of bite angle:
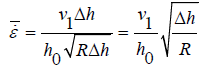 (20)
(20)
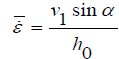 (21)
(21)
Second method
In the second method and for deformation zone, in order to calculate average strain rate in hot rolling, the integration is performed with respect to the variable ϕ
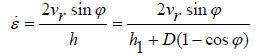 (21)
(21)
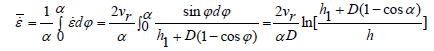 (22)
(22)
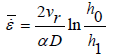 (23)
(23)
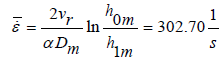 (24)
(24)
For the low value of bite angle:
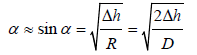 (24)
(24)
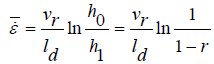 (25)
(25)
Simulation of No-Twist mills by the ABAQUS/Explicit software
In this study in the first stage, the whole roller is given a model by two side grooves. The size of the grooves is achieved by using the caliber maps. Of the two existing grooves on the framework of the side roller, a groove is used in the procedure of No-Twist mills; in fact the other groove plays the role of a substitute. Therefore, the roller height is of no importance in simulation. On the other hand, the inner diameter of the roller, which is the point of bush placement, also bears no significant importance. Due to the fact that simulation is carried out in the ABAQUS software and the cost evaluation of calculation and the time of performing is highly important, only the groove through which the rod passes is defined for ABAQUS. The rollers are defined as “Discrete Rigid” and 3D substances in the ABAQUS. In the hot metal forming procedures, the work piece contains a preliminary temperature which will go through plastic deformation. Some of this plastic work is converted into heat and increases the temperature of the work piece, while due to the fact that the work piece has contact with other tools and owing to being in the outside atmosphere, the work piece temperature decreases through the processes of heat conduction, convection, and radiation. The more the temperature of work piece is changed, the more material behavior is altered [24]. The strain rate was previously mentioned, thus for having a thorough analysis, it is obligatory to define a material behavior complying with the temperature and the strain rate. Therefore, the dynamic Temp-disp. explicit is chosen as a relevant solver. In this approach, the hardening is considered a prerequisite of isotropic. Some references present the thermal property of steel such as Structural Fire Engineering Design [25].
In conditions which contain a high level of deformation during the procedure, the elements get highly deformed. This disarrangement and distortion may bring the solution to a halt and by using the adaptive mesh it can be obviated. In this method, the elements are able to move free of the matter. As a result, the procedure conduction quality stays in an optimum level. Consequently, the place of nodes is changed and the element’s topologies remain unchanged. The entire meshes have the shape of square and they are structured. The improved relation of Ockland, which was acquired by the assistance of a wide range of studies, was provided to the friction. This set portrays the friction coefficient, which is presented in Equation (26), versus roller material and roller velocity.
f = ak(1.05 − 0.0005t) (26)
Section geometry of the rod outlet
The main objective of shape rolling stages is to achieve a distinct section level according to a set of existing standards. Therefore, monitoring of section outlet through different calibers is highly significant. In addition to final section being standard, the produced product in every stage of inter-caliber must be free of any over-breadth and geometry defect. Figure 4 shows the rod section level after exiting stands 1 and 2. The comparison of results with reference of steel company demonstrates a good accordance between finite element and the measured models.
Input and output velocity of rod in each stand
In order to calculate the forward slip, input and output velocity of rod is required in each stand which is achieved by simulation of finite element. Figure 5(A) demonstrates a comparison of velocity between FEM and experimental values for stands 1 to 4 versus three distinct sizes of meshes. According to this figure, it is deduced that different sizes in mesh do not present a significant change and do not alter the output results.
Calculation of forward slip
Results of forward slip in each stand and versus three different sizes of meshes are presented in Figure 5(B).
Influential parameters on forward slip
Impact of coefficient friction: One of the determining parameters in forward slip is the impact of coefficient friction between the roller and the rod. Coefficient friction is only 0.25 to 0.7 in which amounts higher than 0.55 are achievable through sophisticated ragging of the roller surface. In this step, by changing the coefficient friction, the effect of coefficient on the output velocity of rod is investigated. Figure 6 presents that as the coefficient friction increases to a 10% in every step; the forward slip parameter for rolling stands increases.
Rotational velocity of the roller: Alteration in the circuit of operating motor of No-Twist mills or in coefficients of rotary stands leads to a change in the rotational velocity of roller. The rotational velocity of the roller increases towards the end stands. Figure 7 illustrates changes in the forward slip parameter due to the rotational velocity of rollers. Obviously, as the rotational velocity of rollers increases, forward slip decreases in each stand, as it can be concluded from the figures.
Variations in the early temperature of the rod: An increase in the early temperature of the rod brings about a reduction in average plastic rate, consequently, it is expected that slip decreases between the rod and the roller. Figure 8 illustrates changes in forward slip due to an increase in the early temperature of the rod. As it can be concluded forward slip is decreasing in every stand, while the early temperature of the rod is increasing.
Considering the capability of the ABAQUS software in modeling of complex contact conditions and metal forming issues, this set of tools is a proper set for being utilized in hot rolling modeling of the No-Twist mills and rod rolling with high velocity. Parameters such as various finite element meshes, using different size of the meshes, modeling of mechanical and thermal properties of materials, and its capability of providing several desired outlets are the most prominent advantages of the ABAQUS software. Obtaining the mechanical property and plastic strains in the shape rolling, while the section is in such a condition that faces high deformation and strain rate, is necessary for the validity of modeling results. Therefore, the hot tensile test is carried out to attain the mechanical property and plastic strains for the steel of interest. Furthermore, the modulus of elasticity decreases as the temperature increases. Creating a detailed modeling through the rod’s hot rolling of the No-Twist mills can be a suitable tool for anticipating the parameters of interest, some of which are the dimension of surface of outlet section in each stand and forward slip, during the hot rolling of the machines. In addition, considering the accordance between the results obtained from modeling of this research and the manufactory quantities of Isfahan’s steel company, it can be understood the validity of modeling which is performed. Therefore, the method employed may be used as a tool for eliminating and removing the experimental stages and phases.
Regarding the effective role of the velocity of roller and the rod, during a high velocity rolling and a variation between these two parameters, which leads to a slip in the rolling and rod ,as well as the effect of these velocities in the end product geometry, therefore, in this research, while calculating the forward slip parameter in four stands of the No-Twist mills, the effect of the parameters of the rod’s initial temperature and the roller’s rotational velocity on the forward slip parameter studied. By considering the obtained results, it can be concluded that as the initial temperature of the rod raises, the forward slip parameter in each stand declines. An increase in the roller’s rotational velocity marks a decrease in the forward slip. Coefficient friction, functions as a helpful parameter in the forward slip. For the coefficient, according to Okland’s formula, different values were considered, regarding various velocities in stands 1 to 4. Results of the conversion of this parameter in each stand proved that the escalation of coefficient friction in the roller and rod leads to an increase in forward slip in each stage and phase.
The author would like to gratefully thank Dr. M. Mashayekhi, Assistant Professor of Department of Mechanical Engineering at Isfahan University of Technology, and support of Isfahan Steel Company (ESCO) of Iran.
The authors declare no potential conflicts of interest with respect to the research, authorship, and or publication of this article. Also it is certified that the authors received no financial support from a specified company, university or corporation to do the research project. All the presented materials in the paper are from authors own self-supporting.