International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2018) Volume 9, Issue 3
In this work, the cavitation conditions at high temperatures and pressures in acetone containing deuterium were numerically estimated based on multifunction cavitation in conjunction with large microjets. The predicted bubble shrinkage velocity of 1.114 × 103 km/s satisfies the requirement for bubble fusion, which requires a shrinkage velocity greater than 1.00 × 103 km/s. The internal pressure and temperature of a bubble were found to drastically increase to 7.26 × 108 bar and 6.8 × 108°C, respectively, as the bubble radius shrinks from 100 to 0.1 μm. This temperature is sufficient for bubble fusion, which requires a temperature above 1.0 × 108°C. These results suggest that multifunction cavitation may be capable of generating bubble fusion.
Keywords: Multifunction cavitation; Water jet cavitation; Ultrasonic cavitation; High-pressure high-temperature cavitation; Hot spots; Microjets
Taleyarkhan’s group at Oak Ridge National Laboratory (Tennessee, USA) have claimed to have found evidence of nuclear fusion in a beaker filled with an organic solvent subjected to ultrasonic irradiation [1,2]. More recently, Toriyabe et al. [3] investigated the possibility of fusion reactions occurring during ultrasonic cavitation (UC) in a liquid Li target irradiated with a deuteron (d) beam. Although no meaningful bubble fusion events were detected, extremely large enhancements of d+d reactions were occasionally observed. The bubbles produced by UC, a technique commonly employed in sonochemistry are typically several micrometers in size and their collapse can generate microjets with temperatures of several thousand degrees Celsius. In contrast, bubbles produced by water jet (or liquid jet) cavitation methods, such as floating cavitation are several hundred micrometers in size, and their collapse produces microjets with high pressures of approximately 1.0 GPa.
For many years, fusion reactions have been used to raise the temperature of plasmas to investigate several aspects of this state of matter, including the external energy required to increase the temperature of plasma, the conditions of plasma at its critical point, and deuterium–tritium (D–T) reactions. It has been found that, for nuclear fusion to occur, it is necessary for the original nuclei to collide at a speed of over 1.0 × 103 km/s. Thus, the nuclei must experience a pressure of 1.0 × 1011 atm and a temperature of 1.0 × 108°C.
In the present study, a new cavitation method termed multifunction cavitation (MFC) [4-7] which combines the characteristics of both UC and water jet cavitation was applied to the study of bubble fusion. This method involves irradiation with ultrasonic waves to achieve low-velocity floating cavitation. The cavitation velocity and the pressure and temperature inside a bubble in deuterated acetone when employing MFC were estimated theoretically and compared to the values required for fusion.
Shrinkage velocity of a bubble
In recent years, a variety of industrial applications for cavitation processing, including peening, surface and molecular structure modifications, fatigue strength improvement, and surface cleaning, have been identified. Water jet cavitation involves imparting mechanical action to the surface of a material as a result of the extremely high pressures generated during the collapse of microjets close to the surface [8,9]. In contrast, UC is known to generate hot spots that can promote chemical reactions by producing temperatures of several thousand degrees K [10,11]. As noted above, our group has developed and characterized a new form of cavitation termed MFC which combines the properties of both water jet cavitation and UC.
In the bubble nuclear fusion reported by Taleyarkhan et al. [1,2] in 2002, the constrictive temperature and pressure of the bubble were used to achieve fusion. According to their report a supersonic wave was employed to irradiate acetone containing heavy hydrogen leading to cavitation and excited neutrons were detected when the bubbles collapsed. The report states that thermonuclear fusion occurred between the heavy hydrogen atoms under the elevated temperatures and pressures generated during the experiment. However, prior to publication the paper was criticized by many experts because the same results could not be obtained when the work was repeated under the same conditions. At the time of writing, this phenomenon has still not been successfully observed by any researchers other than the original group.
Interestingly, the Research Center for Electron Photon Science (ELPH) of Tohoku University has recently reported that the D-D fusion reaction is promoted significantly when a supersonic wave is used to irradiate liquid Li subjected to a deuteron beam [3]. However, in these studies because only bubbles generated by supersonic wave irradiation were used to promote the fusion reaction, it is not certain that the shrinkage speed and the pressure and temperature inside the bubbles at the time of collapse met the conditions required for nuclear fusion. Therefore, in the present study the shrinkage speed and the pressure and temperature inside a bubble in acetone during MFC were calculated on a theoretical basis to determine if these values meet the requirements for nuclear fusion and to compare these values with those resulting from conventional UC.
If the typical bubble radii obtained during UC and MFC are assumed to be 4 and 100 μm respectively, the pressures at an infinite distance from the bubble when shrinkage stops at a bubble radius of 0.1 μm will be 2.6 and 5.0 bar respectively (Figure 1). This result is obtained from the equation:
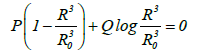 (1)
(1)
Where R is the bubble radius, R0 is the initial bubble radius, P is the pressure at an infinite distance from the bubble, and Q is the initial pressure, which is the acetone vapor pressure.
The shrinkage velocity for a bubble in acetone can also be calculated as:
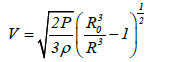 (2)
(2)
Where V is the shrinkage velocity of a bubble with radius R, P is the pressure at an infinite distance from the bubble, and ρ is the density of acetone. From equation (2), the pressures at an infinite distance from the bubble when shrinkage stops at a bubble radius of 0.1 μm will be 2.6 and 5.0 bar for UC and MFC, respectively. The shrinkage velocities of a bubble with a radius of 0.15 μm will be 6.4 and 1.114 × 103 km/s for UC and MFC respectively as shown in Figure 2. As stated previously the initial bubble size for UC was 4 μm whereas that for MFC was 100 μm. At a bubble radius of 0.15 μm which is larger than the radius of 0.10 μm at which shrinkage stops, the shrinkage velocity for the MFC bubble is 1.114 × 103 km/s while the UC bubble has a velocity of 6.4 km/s. Thus, the MFC bubble velocity exceeds that required for bubble fusion.
Multifunction cavitation
Figure 3 summarizes the mechanism by which high-pressure, high-temperature cavitation leads to bubble fusion. This mechanism is associated with our MFC process in which ultrasonic radiation is imparted to the cavitation cloud generated by a high-pressure liquid jet. The resulting microjets produce mechanical action in addition to so called hot spots [12] where chemical reactions can occur. As the ultrasonic cavitation proceeds, isothermal expansion takes place once the pressure is above the Blake threshold value. Following this expansion, Rayleigh shrinkage occurs. Repeated expansion and shrinkage lead to cavitation which in turns results in high-pressure collapse and the generation of high-temperature hot spots. In the conventional heat treatment of metals, the application of heat treatment after cold working is quite different from cold working after heat treatment. In contrast MFC has the capacity to allow so called micro level or Nano level forging, in which the material is simultaneously worked and heat treated.
Blake threshold: The liquid pressure in the vicinity of the bubble wall, pB, may be expressed as follows:
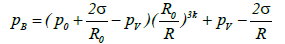 (3)
(3)
Here, the surface tension σ is defined as the surface energy per unit area (equation (3)). In the case of acetone this value is 2.37 × 10-2 [N/m] (J/m2) at 293 K. The other terms in this equation are the bubble radius, R the equilibrium bubble radius, Ro, the static pressure, p0 (typically 1 atm), and the acetone vapor pressure pv.
When the heat exchange between the bubble and the surrounding liquid is negligible, thermally insulated conditions can be assumed and k=γ=Cp/Cv. Here γ is the heat capacity ratio, which is equal to the ratio of the molar heat capacity at constant pressure to the molar heat capacity at constant volume (in the case of air, γ=1.4). If the expansion and shrinkage of the bubbles is minimal the process becomes isothermal and k=1. According to equation (1), in the case of an air bubble with Ro=10 μm in acetone at 20°C, the minimum pressure value of –0.0286 bar occurs at a bubble radius of 19 μm. Therefore, if the liquid pressure falls below this value during the ultrasonic irradiation, the bubble is able to expand greatly.
The minimum value of pB (pB,min) required to expand the bubble can be obtained from the equation:
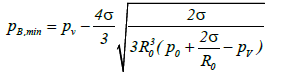 (4)
(4)
When ultra-sonication is applied to the liquid, the liquid pressure at a distance from the bubble wall can be expressed as p0+ps (t). Here p0 is the atmospheric pressure and ps(t) is the pressure induced by ultra-sonication at time t. The time dependent term can be expressed as ps(t)=Asin ωt, where A is the sound pressure amplitude and ω is the angular frequency. Therefore, the minimum value of ps(t) is –A, and the bubble is able to expand at the point at which the value derived from equation (4) equals or exceeds p0–A. This condition can be summarized by the following equation:
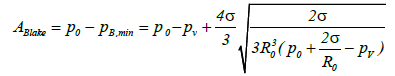 (5)
(5)
Thus, the bubble will overcome the effect of surface tension (that is the Laplace stress) and expand significantly when A≥ABlake, where ABlake is the Blake threshold value [13].
When the bubble radius is less than the equilibrium radius, a high sound pressure is required to expand the bubble. However when the bubble radius is greater than the equilibrium radius, the Blake threshold value will be approximately equal to atmospheric pressure. Therefore, because the diameters of bubbles being circulated in the liquid jet are typically greater than 100 μm, cavitation can readily proceed without the application of particularly high sound pressure.
As noted above, the application of ultra-sonication during conventional liquid jet cavitation (or floating cavitation), generates both high-pressure and high-temperature cavitation through repeated isothermal expansion and compression under thermally insulated conditions.
Multifunction cavitation induced by a low pressure liquid flow: During the flow of an ideal liquid, the external pressure p0 in any infinite direction (that is atmospheric pressure) the pressure in liquid p and the velocity v are related according to Bernoulli’s theorem (equation (6)):
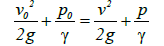 (6)
(6)
Here g is the acceleration due to gravity and γ is the specific gravity of the liquid. From this relationship, the following equation can be derived:
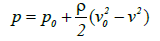 (7)
(7)
Where p (or pv) is the pressure at any arbitrary point and the density of the liquid is expressed by ρ=γ/g.
As p0 decreases or v increases p is reduced. Substituting the pv term of equation (5) for the p term in equation (7) the following formula is obtained, which expresses the conditions required for cavitation expansion (equation (8)):
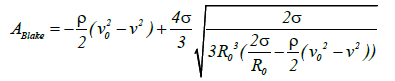 (8)
(8)
The flow rate at a significant distance from the nozzle v0 is zero, and the relationship between v and the Blake threshold value is shown in Figure 4. The flow rate v can be calculated as 5.09 m/s at a Blake threshold value of 1 bar. This result indicates that elevated sound pressure is necessary to expand the cavitation at high flow rates Figure 4.
Multifunction cavitation induced liquid flow circulation: Typically, liquid jet cavitation (or flow cavitation) is accomplished by the application of high-pressure liquid jets generated by nozzles. In such cases the low pressures induced by the whirlpool motion of the fluid result in cavitation.
In the case of a potential flow, the circulation Γ can be defined as follows:
2πru = Γ (9)
This value is not uniform but rather varies with the radius rc of the bubble relative to the internal nucleus. The pressure p at a given rc will be less than the pressure p1 at a wider radius value r1 and may be expressed as follows:
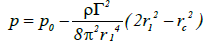 (10)
(10)
Because rc=0 at the nuclear center, the pressure at this center pm represents the minimum pressure and may be calculated as:
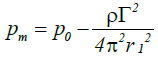 (11)
(11)
When pm (pv) equals the saturated steam pressure at the temperature in the region around the flowing liquid, cavitation will occur. In the case of high-pressure liquid jets from a nozzle, a circulation whirlpool is formed in the vicinity of the nozzle exit resulting in flow cavitation. If the equilibrium radius of the air bubble is R0 and substituting pm for pv (the steam pressure) in equation (5) the conditions necessary for whirlpool cavitation are achieved as expressed in the following equation:
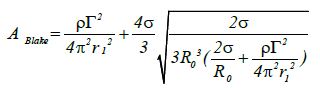 (12)
(12)
At high values of the flow velocity u from the liquid jet nozzle, the circulation is increased. When R0 equals the circulatory nuclear radius r1 the following equation holds true:
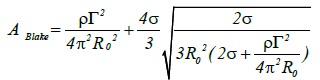 (13)
(13)
Assuming circulation of the nuclear radius, the following expression can also be written:
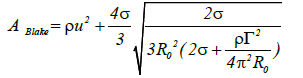 (14)
(14)
Because the first term on the right-hand side of this equation has the greatest effect in terms of increasing the Blake threshold, significant sound pressure is required to inflate the circulation bubble when the circulation becomes overly large Figure 5(a).
Figure 5(b) presents the relationship between u and ABlake at an ABlake value of 1 bar, the value of u is 3.6 m/s. Under these conditions, high sound pressure is needed to inflate the circulation bubble, because the cavitation flow rate in the area of the nozzle exit exceeds 100 m/s. These results predict that multifunction cavitation will take place far from the nozzle exit.
Figure 6 plots the resonance frequencies of bubbles in acetone. These values represent the supersonic wave frequencies resulting from Rayleigh shrinkage and are obtained from the flowing Minnaert resonance equation [14]:
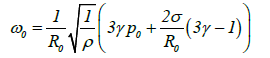 (15)
(15)
Where ω0 is the resonance angular frequency, γ is the specific heat ratio of the gas, p0 is atmospheric pressure, R0 is the equilibrium bubble radius and ρ is the density of acetone. The Rayleigh shrinkage of a bubble with a size greater than 100 μm requires a frequency of less than 37 kHz and in the present study a 28 kHz ultrasonic generator was used.
As noted, combining ultrasonic irradiation with floating cavitation can result in isothermal expansion. In this technique the supersonic wave is a primary wave and the pressure pitch repeats with a wavelength λ. As an example in the case of a sound velocity in acetone of 1,190,000 mm/s, λ is 1,190,000 mm/s/28,000 Hz=42.5 mm when employing a 28 kHz supersonic wave.
Bubble pressure and temperature
The Rayleigh-Plesset equation: The bubble internal gas pressure during shrinkage can be calculated using the Rayleigh–Plesset equation [15,16]:
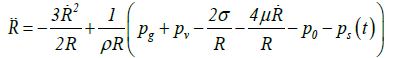 (16)
(16)
where 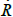 is the velocity of the bubble wall,
is the velocity of the bubble wall, 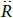 is the acceleration of the bubble wall, σ is the surface tension, μ is the viscosity coefficient for acetone, pg is the pressure of the gas inside the bubble, pv is the vapor pressure of acetone, p0 is the atmospheric pressure, ps(t) is the supersonic sound pressure as a function of time t, and Re is the radius of the air bubble at equilibrium. Additionally pg and ps(t) are respectively defined as:
is the acceleration of the bubble wall, σ is the surface tension, μ is the viscosity coefficient for acetone, pg is the pressure of the gas inside the bubble, pv is the vapor pressure of acetone, p0 is the atmospheric pressure, ps(t) is the supersonic sound pressure as a function of time t, and Re is the radius of the air bubble at equilibrium. Additionally pg and ps(t) are respectively defined as:
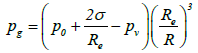 (17)
(17)
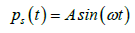 (18)
(18)
Continuous accretion shrinkage leads to many gas molecules remaining inside the bubble as a result of the high shrinkage velocity, such that the pressure inside the bubble continues to increase. A high shrinkage velocity limits the heat flow from the inside of the hot bubble to the outside liquid and allows adiabatic processes to occur. This leads to further increases in the temperature and pressure inside the bubble. As noted, the initial bubble radius values for typical UC and MFC processes were set at 4 μm and 100 μm, and the shrinkage acceleration of the bubble and the pressure inside the bubble were calculated using equation (16).
In this study, the bubbles were irradiated at an acoustic pressure of 1.33 bar. In the case of UC, the shrinkage of a bubble with an initial radius of 4 μm to 0.1 μm generates an internal pressure of 1.10 × 105 bar (1.10 × 104 MPa). In contrast, when employing MFC, the bubble pressure drastically increases to 7.26 × 108 bar (7.26 × 107 MPa) as the bubble shrinks from 100 to 0.1 μm, as shown in Figure 4. The bubble pressure does not reach 1.0 × 1011 bar, which is the pressure required for bubble fusion. It is thought that the necessary pressure could be achieved by increasing the initial bubble size. However, in this work, the bubble size had to be restricted because of some limitation of Excel.
The bubble temperature was subsequently calculated. The thermal energy E of the steam in a bubble depends on the temperature inside the bubble, and varies with expansion and shrinkage. In the right side, clause 1 is work, where neighbouring liquids work for bubbles, clause 2 is heat conduction and clause 3 is the chemical heat of reaction. The bubble temperature T can be calculated from:
E = nCvT (19)
When the change in the thermal energy of the bubble is given by:
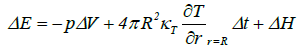 (20)
(20)
where n is the moles of steam in the bubble, Cv is the molar specific heat of the steam, ΔE is the change in the thermal energy, p is the pressure inside the bubble, ΔV is the change in the volume of the bubble, κT is the thermal conductivity of the steam, ∂T/∂r |r=R is the rate of change of the temperature at the bubble wall, Δt is the time step used in the numerical computation, and ΔH is the heat of reaction. The temperature was found to increase significantly to 6.8 × 108°C as the bubble radius shrinks from 100 to 0.1 μm during MFC, whereas in the case of UC, the temperature reaches 3.3 × 108°C when the bubble radius is reduced from 4 to 0.1 μm. In these calculations, ΔH was neglected. The temperature of 6.8 × 108°C resulting from MFC is sufficient for bubble fusion, which requires temperatures over 1.0 ×108°C.
However, the increase in the temperature of the bubble is controlled during shrinkage by the chemical heat of reaction as well as by heat conduction and the thermolysis of the acetone vapor, and this suggests that bubble fusion could occur during MFC (Figure 7). In addition, it is thought that interactions between bubbles could extend the time span over which deuterium is exposed to highly elevated temperatures and pressures.
Keller-Miksis formulation: The Keller-Miksis formulation [17,18] is an equation describing the large radial oscillations of a bubble trapped in a sound field. When the frequency of the sound field approaches the natural frequency of the bubble, large amplitude oscillations will occur. The Keller-Miksis equation takes into account viscosity, surface tension, incident sound waves and acoustic radiation coming from the bubble a factor that was not previously accounted for in Lauterborn's calculations, which solved the equation that Plesset et al. modified from Rayleigh's original analysis of large oscillating bubbles [17]. Keller and Miksis obtained the following equations [18]:
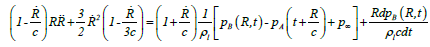 (21)
(21)
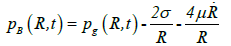 (22)
(22)
where 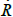 is the velocity of the bubble wall,
is the velocity of the bubble wall, 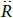 is the acceleration of the bubble wall, σ is the surface tension, μ is the viscosity coefficient for acetone, p0 is atmospheric pressure, pA(t+R/c) is the supersonic sound pressure as a function of time t, c is the velocity of sound, p∞ is the atmospheric pressure, and pB(R,t) is the liquid pressure at the bubble interface.
is the acceleration of the bubble wall, σ is the surface tension, μ is the viscosity coefficient for acetone, p0 is atmospheric pressure, pA(t+R/c) is the supersonic sound pressure as a function of time t, c is the velocity of sound, p∞ is the atmospheric pressure, and pB(R,t) is the liquid pressure at the bubble interface.
Figure 8 presents the pressure and temperature inside bubbles during UC and MFC in an acetone reaction furnace, as calculated using the Keller-Miksis formulation. In the case of UC, the maximum temperature of a bubble is 1.62 × 108°C, which barely satisfies the temperature of 1.68 × 1012°C, which greatly exceeds 1.0 × 108°C, and a maximum pressure of 7.51 × 107 MPa, which is still below 1.0 × 1010 MPa, at a final bubble radius of 0.1 μm. However, both the pressure and temperature resulting from MFC are significantly higher than those produced by UC.
The maximum pressures and temperatures inside the bubbles for UC and MFC in an acetone reaction furnace are summarized in Table 1. The bubble temperature resulting from MFC exceeds the value required for fusion. The pressure produced by MFC does not satisfy the necessary condition, although increasing the bubble radius could increase this pressure. It is also believed that the interactions between bubbles could extend the time during which deuterium is under extremely elevated temperatures and pressures.
| Required pressure | 1.0 × 1010 MPa | Required temperature | 1.0 × 108°C |
| Ultrasonic wave cavitation | 1.25 × 104 MPa | Ultrasonic wave cavitation | 1.62 × 108°C |
| Multifunction cavitation | 7.51 × 107 MPa | Multifunction cavitation | 1.68 × 1012°C |
Footnote: D + T → 4He + n (14 MeV)
Table 1: Maximum internal pressures and temperatures of bubbles during UC and MFC in an acetone reaction furnace and required pressure and temperature of D-T reaction.
It is shown below by the fundamental theory of fluid dynamics [19] that the bubble wall velocity at the collapse never exceeds the sound velocity in the liquid at the bubble wall (cL`) [20].
Consider a liquid flow with no friction. According to the Euler required value of 1.0 × 108°C, while the maximum pressure of a bubble is 1.25 × 104 MPa, which is less than the required value of 1.0 × 1010 MPa, at a final bubble radius of 0.1 μm. MFC generates a maximum equation,
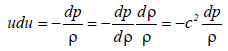 (23)
(23)
Where u is the velocity of the liquid, p is the pressure, r is the density and c is the sound velocity (c2=dp/dρ). Using the Mach number M=u/c equation (23) becomes,
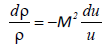 (24)
(24)
On the other hand, the continuity of fluid (liquid) requires,
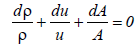 (25)
(25)
Where A is the cross section of the liquid flow perpendicular to the flow direction from equations (24) and (25),
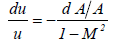 (26)
(26)
From equation (26) it is required that when M>1, the cross section must increase (dA>0) if the fluid velocity increases (du>0). At the bubble collapse, the velocity of the liquid increases towards the bubble, this is required by the fluid (liquid) continuity. Thus, for M>1 the cross section should increase. However, the cross section of the liquid flow decreases towards the bubble due to the spherically contracting geometry. Thus it is concluded that M never exceeds 1; in other words the liquid velocity never exceeds the sound velocity of the liquid. It implies that the speed of the bubble collapse, which is the liquid velocity at the bubble wall and never, exceeds the sound velocity of the liquid at the bubble wall. However, during the interaction among bubbles the microjets are formed. Because the microjets do not have the spherically contracting geometry (Figure 3), the cross section does not have to increase (dA>0) and the cross section should decrease (dA<0) during the formation of microjets. Therefore, there is a chance that the liquid velocity could exceed the sound velocity of the liquid.
In single-bubble sonoluminescence (SBSL) it is known that the emission spectrum tends to reach a peak with ultraviolet rays and strongly depends on the type of gas dissolved in the liquid. Small amount of tracking noble gases or other impurities drastically alter the amount of light radiation. It has also been found to be affected by small changes in other operating parameters (primarily operating pressure, dissolved gas concentration and liquid temperature). Therefore, when designing an experimental apparatus based on the results analyzed in this research it is necessary to evacuate heavy acetone. Estimation of bubble temperature is performed by Sonoluminescence (SL). Sonoluminescence is the phenomenon whereby pulsating bubbles focus diffuse sound energy by 12 orders of magnitude [21] to generate extremely short flashes of ultraviolet light [22-24].
For 20 to 30 years, the multibubble sonoluminescence (MBSL) spectrum has been experimentally studied. In particular, MBSL of water contains significant emission of excited OH radicals. The MBSL spectrum has characteristic spectral lines such as OH line and Na line in sodium chloride aqueous solution. However, SBSL is a continuous spectrum with no characteristic spectral lines. Also the pressure and temperature achieved within one bubble in MBSL are considered to be smaller than SBSL. It is concluded that the difference between SBSL and MBSL is the ultimate pressure and temperature inside the bubble. Water jet cavitation in this study is MBSL. The cavitation bubble field of bubble collapse is a pseudo SBSL, and it is considered that the molecular radiation disappears. Also if the sound pressure is very large, Giri and Arakeri have reported that there is an MBSL spectrum similar to SBSL [25].
The maximum 6 eV photon energy observed for water bubbles is limited only by the extinction coefficient of the liquid. If the energy density within the collapsed bubble concentrates 1000 times, and if the bubbles contain deuterium gas, the kinetic energy of the individual ions is sufficient to generate thermonuclear fusion [26].
It is historically known that liquids with a high vapor pressure such as acetone bubble easily by neutrons, but emit very weak light. Therefore, bubble nuclear fusion using acetone involves the possibility of energy density concentration. Parameters such as bubble diameter, inner wall velocity, internal temperature and pressure, which are affected by various driving pressure amplitudes in heavy acetone at 0°C, have been investigated by analysis. The internal pressure at the time of collapse of heavy acetone vapor bubbles is very high, and the pressure inside the bubble rises due to the increase in the sound pressure amplitude. The maximum internal temperature of the cavitation bubbles induced by the sound pressure in heavy acetone increases with the sound pressure and is much higher than the maximum temperature induced by the sound pressure in a liquid containing water and acid. However for degassed acetone, the SL signal is very weak and it cannot be ruled out the possibility that in the limit of perfect degassing SL also vanishes.
Dynamics of bubbles are being investigated under typical experimental conditions in heavy acetone. Expecting high compression conditions suitable for thermonuclear fusion, the phase change coefficient (ratio of staying without being thermally decomposed) α is greatly different between heavy acetone and heavy water. The phase change coefficient α of heavy acetone is about 1.0 [27] which is much lower than the phase change coefficient α of deuterated water of about 0.075 [28-30]. Therefore, heavy acetone is advantageous for bubble nuclear fusion under high temperature and high pressure compared to heavy water.
In the present study, the temperature of supersonic wave bubble with the initial radius of 4 μm becomes 1.62 × 108 K, which is larger than 107 K [31]. However, the elevated temperature and pressure by upsizing of initial bubbles is apparent. Because N. Zoghi-Foumani, R. Sadighi-Bonabi investigated the temperature and pressure as the initial bubble radius of 5.10 μm, it is thought that the temperature and pressure increases remarkably in the case of 100 μm. In addition, the further elevated temperature and pressure can be expected because it is thought that the supersonic wave is irradiated to the SBSL-like bubble [25].
The case when the sound pressure of the ultrasonic wave was increased from 1.32 atm to 2.64 atm was compared by analysis (Figure 9). Here the pressure and temperature when WJC with a radius of 100 μm is irradiated by ultrasonic wave, subjected to Rayleigh contraction up to 2 μm after isothermal expansion, are calculated using Rayleigh- Plesset equation. The bubble pressure at 2 μm shrinkage is 1,020 MPa at both 1.32 atm and 2.64 atm there is no difference. On the other hand, the bubble temperature is 3,520 K at 1.32 atm, and 51,500 K for calculation at 2.64 atm. As described above, there is no change in the pressure of bubbles but the temperature is relatively increased at 2.64 atm, increasing the ultrasonic output makes it possible to increase the energy density.
By assuming that a fraction of the vapour molecules present in the bubble at its maximum radius escapes condensation, it is straightforward to show that the modified expression [32] for the energy density of Ed becomes:
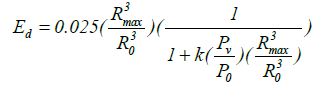 (27)
(27)
Here k is the fraction of vapour escaping condensation and Pv is the vapour pressure of the host liquid. The plot of Ed versus expansion ratio Rmax/Ro is presented. It is known that the constant value for fusion threshold is 104 eV per atom or molecule [32] (note: 1 eV=11,600 K). The value of k=0.025 is chosen on the basis of results due to Storey and Szeri [33]. In the case with k=0.025 and Pv/Po=10-5 (typical of fluids like ethylene glycol and Po=1 bar), the required energy density Ed seems possible with expansion ratio of about 75. If the k value of acetone is relatively low, the required energy density Ed seems possible. If the ratio of steam escaping condensation in heavy acetone can be estimated, the enlargement ratio of bubbles exceeding the threshold can be obtained.
Figure 10 shows the relationship between bubble energy density Ed and expansion ratio,Rmax/Ro in case of acetone. Here, in case of acetone Pv/Po=0.242 and if the fraction of vapour escaping condensation k is a small value of 1 × 10-6 the energy density Ed can exceed the threshold of 1 × 104 eV/atom, when Rmax/Ro becomes over 77. The constant value for fusion threshold, 104 eV per atom or molecule (note: 1 eV=11,600 K) is also shown in Figure 10. This energy density corresponds to 1.19 E × 108 K. The bubble temperature T can be calculated from the equation (19) in the temperature of Figure 7, Figure 8 and Figure 9. Here the initial bubbles had the number of moles in the standard state and it was assumed that the number of moles varied depending on the volume which changes with the expansion and shrinkage of the bubbles. This is an assumption that the vapor in a bubble flowed from the bubble wall at the time of expansion and flowed out from the bubble wall at the time of shrinkage like breathe. As shown in equation (20) the energy in a bubble increases mainly due to pressure and volume change but if the number of moles of steam remaining in the bubble is too much, a temperature rise cannot be expected. On the other hand, assuming that the same number of moles n in the bubble is kept constant, the temperature when the bubble of the radius Ro 100 μm shrinks to the radius Rmin 0.1 μm is 3.81 × 105 K as shown in Table 2. The temperature rises as the proportion k of residual acetone decreases due to evaporation or thermal decomposition, etc. When the fraction of vapour escaping condensation becomes less than 1 × 10-6, the temperature rises to 3.16 × 106 K according to the equations 19-22. It is necessary to increase the expansion ratio, Rmax/Ro and decrease the fraction of vapour escaping condensation, k in order to obtain high energy density Ed and achieve the bubble fusion. Here, in order to increase the enlargement ratio of heavy acetone bubbles it is necessary to further increase the sound pressure. Then an energy density of 104-105 eV (10-100 keV) exceeding the threshold can be achieved.
| Fraction of vapour escaping condensation (%) | 100 | 71.2 | 0.03 | 9.61E-07 | 1.09E-07 |
| Temperature reached (K) | 3.811E+05 | 4.496E+05 | 1.178E+06 | 3.159E+06 | 1.321E+12 |
Table 2: Temperature when air bubbles shrink from 100 μm to 0.1 μm.
We have developed various kinds of technology to increase the temperature and pressure of a cavitation bubble in multifunction cavitation. The liquid used for the experiment is water. The basic results with water can be applied to other liquids such as deuterated acetone. For the experiment on bubble fusion, the required experimental conditions for bubble fusion are shown in Table 3. The pump discharge pressure is an important factor to produce high-pressure microjets. A pump discharge pressure of more than 35 MPa is necessary in order to obtain the collapse pressure of microjets. The number of cavitation bubbles depends on the liquid flow rate. However, for example, the rated flow rate of 15 L/min tends to decrease because of pressure loss before the injection from the nozzle. The typical flow rate is indicated in Table 3. The diameter of the liquid jet nozzle influences the size of cavitation, the flow rate and the velocity of the liquid jet. The typical diameter is less than 1 mm as shown in Table 3. The stand-off distance, which is the distance between the water jet nozzle and target to decrease the velocity of cavitation, is shown in Figure 3. In order to expand the bubble, the moving velocity of liquid jet cavitation must be decreased as shown in Figure 4 and Figure 5. At the second peak of 65 mm, a lot of cavitation exists and this is named the best position to stop the moving liquid jet cavitation. However, the stand-off distance depends on the nozzle diameter and pump discharge pressure. An ultrasonic frequency of 28 kHz is appropriate as the acetone bubble resonance frequency for liquid jet bubbles larger than 100 μm. The dual ultrasonic mode that is proximity two frequency switching oscillation is effective to provide the residual compressive stress, improve the corrosion resistance and change the microstructure by annealing at a temperature of about 700°C on the material surface. Here, the topmost surface temperature is restricted because the heat capacity of the material is high even if the bubble temperature is extremely high such as 1.68 E+12°C. The oscillator nozzle distance is set to be 54 mm, which is one wavelength of the ultrasonic frequency 28 kHz. As the distance is shorter, the sound pressure is higher and the number of cavitation bubbles, which can be expanded, increases. However, the sound pressure is the same at the point one wavelength from the oscillator. The reactor shape should be the smallest cylinder because the cavitation can be concentrated and the cavitation density becomes higher. Moreover, the swirl flow nozzle (SFN) [34] is set as the liquid jet nozzle, as shown in Figure 3. The cavitation generated from the liquid jet nozzle expands in SFN and the number of cavitation bubbles increases in SFN. This leads to ultrahigh temperature and ultra-high pressure cavitation bubbles by the ultrasonic irradiation. In order to detect the nuclear fusion reaction, a neutron detector and a photomultiplier must be installed around the reactor.
| Liquid | Deuterated acetone |
|---|---|
| Pump discharge pressure | 35MPa |
| Liquid flow rate | 7 L/min |
| Diameter of liquid jet nozzle | 0.8 mm |
| Stand-off distance* | 65 mm |
| Ultrasonic frequency | 28 kHz |
| Ultrasonic mode | Dual |
| Oscillator-nozzle distance | 54 mm** |
| Reactor shape | Cylinder |
| Swirl flow nozzle | Equipped |
| Neutron detector (Plastic liquid scintillator) | Equipped |
| Photomultiplier tube | Equipped |
*Distance between water jet nozzle and target to decrease the velocity of cavitation
**Wavelength of ultra-sonication
Table 3: Required experimental condition for bubble fusion.
The end goal of this optimization research on bubble fusion is to detect the neutron and energy caused by bubble fusion.
The cavitation collapse conditions for MFC in acetone containing deuterium in conjunction with large microjets at high temperatures and pressures were numerically estimated. The following conclusions were obtained:
1. A shrinkage velocity of 1.114 × 103 km/s in the MFC bubble satisfies the velocity condition necessary for bubble fusion, which requires a velocity of over 1.0 × 103 km/s.
2. During MFC, as the bubble shrinks to 100 to 0.1 μm, the pressure and temperature inside the bubble drastically increase, possibly leading to temperature, pressure and energy density that satisfy the conditions of bubble fusion.
This research was supported in part by JSPS KAKENHI Grant Number 16K06029 (Grant-in-Aid for Scientific Research (C)) and by the Light Metal Educational Foundation, Inc.