Tumors are a family of high-mortality diseases, exhibiting a derangement of cellular proliferation which often lead to uncontrolled cell growth [1,2]. Research efforts are being devoted to understand the interaction between the tumour cells and the immune system [3-6]. Mathematical models, using ordinary differential equations with integer-order, have been proven valuable in understanding the dynamics of tumour-immune system and how host immune cells and cancerous cells evolve and interact; See e.g. [7-12]. However, modeling of biological systems by fractional-order differential equations has more advantages than classical integer-order mathematical modeling, in which such affects the memory are neglected. Accordingly, the subject of fractional calculus (that is, calculus of integral and derivatives of arbitrary order) has gained popularity and importance, mainly due to its demonstrated applications in system biology [13,14] and other fields of sciences [15-18]. The Fractional-Order Differential Equations (FODEs) models are more consistent with the biological phenomena than those of integer-orders. This is due to the fact that fractionalorder derivatives the description of the memory and hereditary properties inherent in the processes [19]. It has been deduced in [13] that the membranes of the organism have fractional-order electrical conductance, which are classified under the non-integer order models.

Immune system is considered as one of the most fascinating schemes in terms of biology and mathematics. Immune system is multi-functional with several metabolic pathways; therefore most effector cells perform more than one function. Plus, each function of the immune system is typically done by more than one effector, which makes it more complex [20]. Differential equations, with integerorders, have long been used in modeling cancer phenomena [21-23], but fractional- order differential equations have short history in modeling such systems with memory [24]. Herein, we use FODEs in modeling tumor-immune interactions, which are naturally related to systems with memory.

Assume that model of cancer-immune system includes two immune effectors: E1(t) and E2(t) (such as cytotoxic T-cells, and natural killer cells), interacting with the cancer cells, T(t) with tumour’s functional response of Holling Type-III [25]. The model takes the form

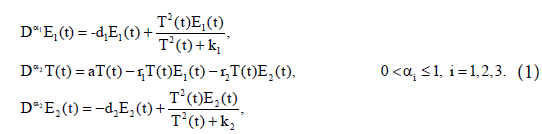
The parameter d₁ represents natural decay rate of the effect cells E₁(t). k₁ and k₂ are half saturation parameters, a is the growth rate of tumour cells. r₁ and r₂ are the reduction rate of tumour cells due to presence of the effector cells E₁(t) and E₂(t) respectively. d2 represents natural decay rate of the effect cells E₂(t). All of these parameters are supposed to be positive constants. The interaction terms in the first and third equations of model (1) satisfy the cross reactivity property of the immune system. It has been assumed that (d₁k₁/(1−d₁))<<(d₂k₂/(1− d₂)), to avoid the non-biological interior solution where both immune effectors coexist. For more details about model (1), we refer to [16].

Here, we have modified model (1) to include external sources of effector cells and immune stimulation effects by treatment Interleukin-2 (IL-2). Assume that three populations of the activated immune-system cells, E(t); the tumor cells, T(t); and the concentration of IL-2 in the single tumor-site compartment, IL(t) (Figure 1). To ease the analysis, consider a classic bilinear model that includes Holling Type-I function and external effector cells s₁ and input of IL-2, s₂. The interactions of the three populations are then governed by the fractional-order differential model:

Figure 1: Key-players in tumour-immune interactions described in model (2).

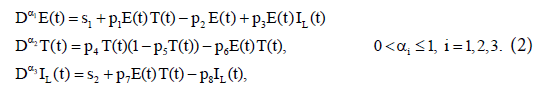
with initial conditions: 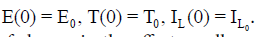. The first equation describes the rate of change in the effector cells population. The parameter p₁ represents the antigenicity rate of the tumor (immune response to the appearance of the tumor), p₃ is the cooperation rate of effector cells with Interleukin-2 parameter, and s₁ represents the external source of the effector cells, with rate of death p₂. The second equation shows the rate of change of the tumour cells which follows a logistic growth (a type of limiting growth) in the absence of immune response. The parameter p₄ incorporates growth rate of tumor cells. The maximal carrying capacity of the biological environment for tumor cell is p⁻¹₅ . Whereas, p₆ is the rate of tumor cells. The third equation gives the rate of change for the concentration of IL-2. Its source is the effector cells, which are stimulated by interaction with the tumour. The parameter p₇ is the competition rate between the effector cells and the tumor cells. The external input of IL-2 into the system is s2 and the loss-rate parameter of IL-2 cells is p₈.

In the absence of immunotherapy with IL-2, we have

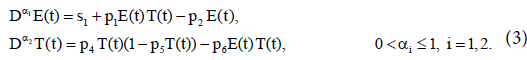
To minimize sensitivity (or robustness) of the model, we nondimensionalize the bilinear system (3) by taking the following rescaling:

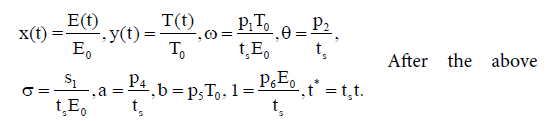
substitution into (3), we have

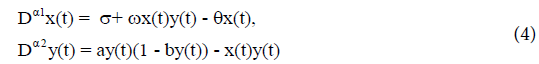
(Here t is replaced by t*.) The analytical stability region of fractionalorder system (4) is given in Figure 2.

We then study the stability of the steady states of models (1) and (4).

Equilibria and local stability of model (1)

The equilibrium points of system (1) are:

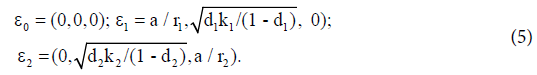
Here ε₀ is the naive first equilibrium, ε₁ is the memory equilibrium and the ε₂ is endemic according to the value of the tumor size. Stability analysis shows that the naive state is unstable.

However, the memory state is locally asymptotically stable if

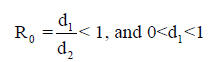
While the endemic state is locally asymptotically stable if 0 R > 1 and 0 < d₂ < 1. There is bifurcation at R0=1. The stability of the memory state depends on the value of one parameter namely the immune effector death rate.

Equilibria and local stability of model (4)

The steady states of the reduced model (4) are again the intersection of the null-clines 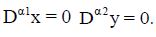If y=0, the tumorfree equilibrium is at 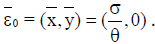This steady state always exist, since 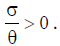From the analysis, it is easy to prove that the tumorfree equilibrium 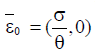of the model (4) is asymptotically stable if threshold parameter (the minimum tumor-clearance parameter) 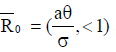and unstable if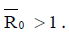

However, if y≠0, the steady states are obtained by solving

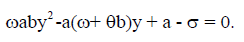
In this case, we have two endemic equilibria,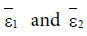

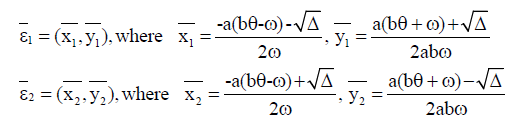
with 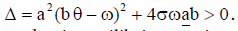The Jacobian matrix of system (4) at the endemic equilibrium ε₁ is

Figure 2: Stability region of the fractional-order system (4) is enlarged when 0<α ≤ 1, where λ is the root of the characteristic equation.

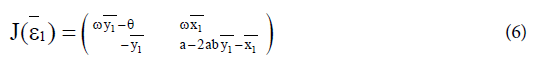
Proposition 1: Assume that the endemic equilibrium ε₁ exists and has nonnegative coordinates.

If 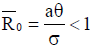then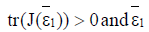 is unstable.

Proof Since

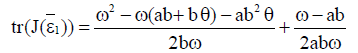
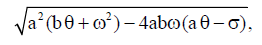
then inequality 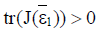is true if

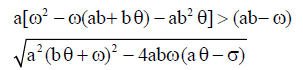
Therefore, when 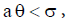we have 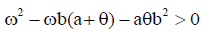and hence both sides of the inequality are positive. Therefore if the equilibrium point exists and has nonnegative coordinates, then 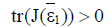and the point (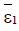) is unstable whenever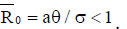

Similarly, we arrive at the following Proportion.

Proposition 2: If the point 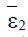exists and has nonnegative coordinates, then it is asymptotically stable.

Proposition 3: The presence of a fractional differential order in a differential equation can lead to a notable increase in the complexity of the observed behaviour, and the solution is continuously depends on all the previous states (Figure 1).

The numerical technique discussed in [16] was used to numerically simulate the qualitative behaviours of the fractional-order models. The numerical technique is based on Caputo sense for fractional derivative (Appendix A) and implicit Euler’s approximation, for the resulting systems, with step-size h=0.05 and 0.5<α ≤ 1 and parameters values given in the captions of the figures.

Figure 2 provides indication that the fractional differential order enlarges the stability region of the solution when 0<α ≤ 1. Figure 3 displays the numerical simulation of (1). The left banner shows the memory equilibrium point ε₁ ; While right banner shows an endemic equilibrium ε₂ with sustained oscillations. Figures 4 and 5 confirm that the fractional derivative damps the oscillation behaviour for model (1).

In this paper, we presented two fractional-order models for tumorimmune interactions. In the first model, we provide a Holling type- III function and cross reactivity in fractional-order model for tumorimmune interactions. Two immune effectors have been considered because of the property of multi-functional and multi-pathways of the immune system. We obtained memory states, using the fractionalorder, whose stability depends on the value of one parameter namely the immune effector death rate. However, in the second model, we extend the model to include external treatments then reduce the system into a prey-predator model. The models possess non-negative solutions, as desired in any population dynamics. We deduced the threshold parameters Rand 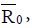respectively for each model. These parameters represent the minimum tumor-clearance parameter or minimum infection free. It has been seen from the numerical simulations that the fractional-order enriches the dynamics of the system and enlarges the stability regions of the solutions. Although the fractional-order model (4) is simple, it displays up to three steady states. Figure 6 shows different types of steady states: Tumour-free steady state 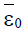, dormancy-, medium and high persistent-tumour steady states (right) 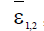for the model (4).

Figure 3: Shows the numerical simulations of model (1) when α=1.0 and a=r₁=r₂=1; d₁=0.3, d₂=0.7, k₁=0.3, k₂=0.7 (left banners) where the system converges to steady state ε₁ ; and when d₁=0.7, d₂=0.3 (right banner), where the system converges to steady state ε₂ . We note sustained oscillations.

Figure 4: Shows the numerical simulations of model (1) when α=0.95 and a=r₁=r₂=1; d₁=0.3, d₂=0.7, k₁=0.3, k₂=0.7 (left banners) where the system converges to steady state ε₁ ; and when d₁=0.7, d₂=0.3 (right banner), where the system converges to steady state ε₂ . The fractional derivative damps the oscillation behaviour.

Figure 5: Shows the numerical simulations of model (1) when α=0.75 and a=r₁=r₂=1; d₁=0.3, d₂=0.7, k₁=0.3, k₂=0.7 (left banners) where the system converges to steady state ε₁ ; and when d₁=0.7, d₂=0.3 (right banner), where the system converges to steady state ε₂ . The fractional derivative damps the oscillation behaviour.

As a result, in the endemic steady states, Figure 7 shows that the fractional-order derivative kills the oscillation behaviour. Figure 8 displays the numerical simulations for the model (4) with different values of the fractional order and parameter values given in the caption. The tumour-free 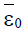is locally asymptotically stable as 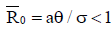.From the graphs, it can be seen that FODEs have rich dynamics and are better descriptors of biological systems than traditional integerorder models. The equilibria for infection-free and endemic fractionalorder cases are the same as integer-order counterparts.

In this paper, the authors conclude that the fractional-order derivatives in the models provide an excellent instrument for the description of memory and hereditary properties of inter and intra cells. It is possible that the tumour may result in either equilibrium with (dormancy) or escape from the immune system. The fractionalorder differential equations are, at least, stable as their integer-order counterparts. The presence of a fractional differential order in the differential equation can lead to a notable increase in the complexity of the observed behaviour, as the solution continuously depends on all the previous states of the solutions. The analysis can be extended to include more components of immune response and control variables. It can also be extended to describe the dynamics of hepatitis B and C virus infections.

The subject of fractional calculus deals with the investigations of derivatives and integrals of any arbitrary real or complex order, which unify and extend the notions of integer-order derivative and n-fold integral. Here, we provide some definitions of fractional-order integration and fractional-order differentiation [26]. There are several approaches to the generalization of the notion of differentiation to fractional-orders e.g. Riemann-Liouville, Caputo and Generalized Functions approach. Let 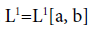be the class of Lebesgue integrable functions on [a, b], .

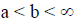Figure 6: Shows (left) tumour-free steady state 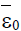and low-, medium and high persistent-tumour steady states (right) 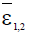,for the model (4). The stable steady states are [•], unstable steady states are [◦], stable manifold is [−−−] and initial conditions are [+], with external treatment doses σ>0 and particular parameters.

Figure 7: Shows numerical simulations of model (4) when s=0.1181, ω=0.1184, θ=0.1747, r=0.636, b=0.002. _α₁=α₂=1, 0.9, 0.7. Note that is locally asymptotically. The fractional-order derivative kills the oscillation behaviour.

Figure 8: Shows the numerical simulations of model (4) when σ=0.1211, ω=0.1184, θ=0.3746, a=1.635, b=0.002.α₁=α₂=1, 0.9, 0.7. is locally asymptotically stable as

Definition 1 The fractional-integral (or the RiemannLiouville integral) of order 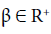of the function is defined by

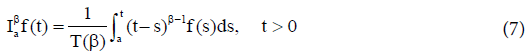
The fractional derivative of order aε(n−1,n) of f(t) is defined by two nonequivalent approaches.

(i) Riemann-Liouville fractional derivative in which we take fractional integral of order (n− α) and then take nth derivative,

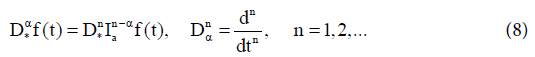
(ii) Caputo fractional derivative in which we take nth derivative and then take a fractional integral of order (n− α)

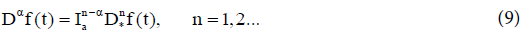
From the definition, we notice that the time-fractional derivative of a function f(t) at t=t_n involves an integration and calculating timefractional derivative that requires all the past history, i.e. all the values of f(t) from t=0 to t=tn. In this paper, we have adopted Caputo’s definition which has the advantage of dealing properly with initial value problems. The following Remark addresses some of the main properties of the fractional derivatives and integrals [12,17].

Remark 1

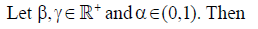
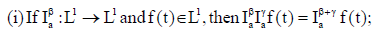
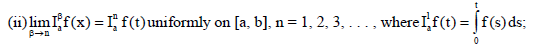
(iv) If f(t) is absolutely continuous on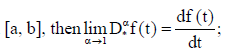

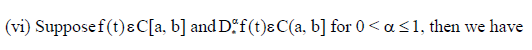
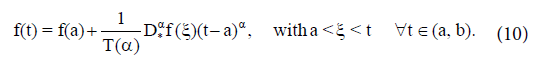
If (vi) holds, and then f(t) is nondecreasing for each 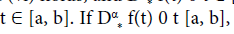then f(t) is non-increasing for each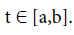

The work is supported by Center-Based ZCHS-12-2014 and UPAR Projects, UAE University. The authors are grateful to the reviewers and Editor Shonisani C Tshidino for their valuable suggestions and constructive comments which improved the manuscript.