Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2013) Volume 2, Issue 2
This paper aims to examine whether the mean-variance frontier generated by benchmark portfolios can be expanded by adding all sorts of IPO portfolios, thus the investors can get improvement in investment opportunity sets. To form the benchmark portfolios, firstly, we investigate the factors which capture the cross-sectional variation in average monthly stock returns on Chinese main board A-share market from 1999 to 2010, and the result shows that BE/ME (book-to-market equity) and liquidity have the most significant power to explain the stock returns by using univariate sorting test, univariate and multivariate cross-sectional regressions methods. Then using spanning and step-down procedure, we come to some significant conclusions: in the short run, industrial IPO portfolios of medicine industry can significantly expand the mean-variance frontier; in the long run, industrial IPO portfolios with rag trade, transportation industry, metal industry and all stocks have the ability to improve the investment opportunity sets for mean-variance investors. The outcome has a vital implication for both financial institutions and investors.
<Keywords: Chinese stock market, IPO, Spanning, Step-down, Mean-variance
Along with the development of Chinese stock market, initial public offerings (IPOs) have been attracting more and more considerable attentions over the recent ten years from both academic researchers and practitioners. Most of them focus on the research of the Chinese IPO underpricing phenomenon. Summarizing their standpoints, we can attribute the IPO underpricing to lack of alternative investment choices, imbalance between supply and demand of IPOs, IPO offering price setting, time gap between IPO announcement day and first trading day, severe information asymmetry and so on. They investigate the long-run performance of Chinese IPOs. Some of their studies show that the performance of IPOs outperform the market, however, some are opposite. Besides the IPO underpricing and long-run performance, some researchers also study on the ownership of the IPO such as Wang [1]. However, there is no research focusing on the issue whether Chinese IPO stocks, as new assets, can significantly expand the meanvariance frontier generated by seasoned stocks (benchmark portfolios), thus leading to diversification benefits. This research issue is important for both financial regulation institutions and mean-variance investors. If the outcome is affirmative, it means the IPO in Chinese market is more effective and efficient, and it also means that there is room for investors to develop the IPO-related products to gain diversification benefits from these products. On the contrary, if the outcome does not support the IPOs’ ability of diversification, the development of IPOrelated products will be limited for both financial institutions and mean-variance investors.
The earliest research on this issue can be traced back to the research on the US IPO portfolio formed on equal-weighted and value-weighted ways from 1977 to 2002. They sort all the sample IPO stocks into venture backed and non-venture backed IPOs, IPOs with and without prestigious underwriters, and nine industry IPO portfolios. They use 25 decontaminated size/book-to-market ratio portfolios from US common stocks as the benchmark portfolios. Their conclusion shows that a value-weighted rather than equal-weighted IPO portfolio such as venture backed IPOs, IPOs with prestigious underwriters and business service, computer and health care IPOs can lead to a statistically and economically significant enlargement of the mean-variance frontier originally generated by the benchmark portfolios. Chen and Ho [2] investigate two indices: IPOX 30 and IPOX 100 compiled by IPOX Schuster LLC. on the US stock market from 1980 to 2006. For the benchmark portfolios, they use 25 Fama-French value-weighted size/ book-to-market portfolios comprising NYSE, AMEX and Nasdaq stocks. To find the effect of internet bubble on the IPOs, they separate the whole time sample into two segments: 1980-1998 and 1999-2006. They conclude that both IPO indices can expand the mean-variance frontier generated by the benchmark portfolios. Furthermore, the enlargement effect of the IPO indices is much more significant during the pre-Internet bubble period than the post-Internet bubble period.
The key component of the research above is how to form the benchmark portfolios, i.e. according to the factors which can influence the cross-sectional variation in average monthly returns. The earliest research on this topic can be traced back to Sharpe [3] and Lintner [4] who initially develop CAPM implying that beta is the only factor which can significantly explain the stock returns. Banz [5] confirms the small size effect and finds that small firms earn 0.4% averagely more than large firms when testing the US stock market. The cornerstone study on BE/ME (book-to-market equity) can be traced back to Stattman [6] who shows a positive relationship between expected stock returns and BE/ME in the US stock market. Fama and French [7] also find the significance of BE/ME to explain the stock returns in US stock market, and BE/ME can absorb the role of E/P (earning-to-price ratio), leverage and some of the firm size. The most influential work on liquidity effect owes to Amihud et al. [8] who tests the relationship between stock returns and liquidity measured by quoted bid-ask spread during the period of 1961-1980. They find that less liquid assets require more expected returns compared with more liquid assets. Besides the factors mentioned above, other variables are also examined in the previous studies including E/P (earning-to-price ratio), D/P (dividend-to-price ratio), and C/P (cash flow-to-price ratio). For example, Basu [9] finds a negative relationship between stock returns and E/P on US stock market. Rozeff [10] provides an empirical support for the use of the D/P to explain the expected stock returns. Lakonishok et al. [11] finds C/P is capable of explaining the stock returns in the Japanese market. Among the related literatures on Chinese stock market, Drew et al. [12] find that stock returns have negative relationships with ME and BE/ ME but have no relationship with beta. Additionally, Wang and Iorio [13] confirm the invalidity of beta, E/P and D/P in explaining the stock returns. For the liquidity, Wang and Chin [1] find that low-liquidity stocks outperform high-liquidity stocks when investigating the Chinese stock market. This paper researches the issue whether Chinese IPO stocks can significantly expand the mean-variance frontier and thus leading to diversification benefits on each sort of the IPOs. The structure is as follows: Section 2 introduces the methodology and the data. Section 3 reports and discusses the empirical results. This section includes two parts, the first part is to test and find the main influencing factors which can explain the cross-section of Chinese stock returns, the second part is to report the results of which sort of Chinese IPO stocks can significantly expand the mean-variance frontier in Chinese market. The final section concludes.
Our test covers the whole period from 1999 to 2010 in Chinese stock market. Since the number of IPO decreased rapidly to about 10 per year after 2004, the whole period is separated into two segments: one is from 1999 to 2004, the other one is from 2005 to 2010. For the first half period, all of the IPOs are classified into nine groups according to their industries. The IPO portfolios of all of the IPOs and nine specific industries are tested separately within this period. For the second half period, we only test the IPO portfolios with all of the IPOs as a result of the limited number of IPOs. Furthermore, IPO portfolios of all of the IPOs which covers the whole period is also tested. To observe the short-run and long-run performance, we test all of the IPO portfolios’ one-year and two-year ability to expand the mean-variance frontier respectively.
To form the IPO-indices and the benchmark portfolios, we get the monthly closing price, annual volume of total shares, annual book equity (stockholder’s equity), annual earning, annual dividend, annual cash flow and liquidity measured by monthly turnover rate (the number of shares traded divided by the number of shares outstanding in that stock) of all the main board A-shares listed on the Shanghai Stock Exchange and the Shenzhen Stock Exchange from the database Wind Information Co., Ltd (Wind Info).
To obtain the monthly return of every IPO portfolios, we include all qualified IPOs listed within the last twelve months to test their one-year performance. Similarly, we include all qualified IPOs listed within the twelve months before the past twelfth twelve month to test their twoyear performance. We select two methods including equal-weighted and value-weighted to form IPO portfolios. For the period from 1999 to 2004, all of the IPOs are classified into nine groups according to their industries, including realty industry, rag trade, mechanical installation, transportation industry, metal industry, chemical industry, food service industry, information technology and medicine industry, and for each group we construct one portfolio. However, as the number of IPO stocks is very small for the period from 2005 to 2010, we construct only one portfolio including all IPO stocks of each year.
For the benchmark portfolios, we include all of the stocks listed at least two years before so as not to overlap with the IPOs. Through univariate sorting test and multivariate cross-sectional regressions below, we find that liquidity (turnover rate) and logarithm of the bookto- market equity (ln(BE/ME)) have the most significant power to explain the Chinese A-share main board stock returns. At the beginning of each year, we sort all of the stocks which meet our requirements above into 25 portfolios based on their value of turnover rate and ln(BE/ME). To be specific, we find the points of one fifth for the value of both turnover rate and ln(BE/ME), then we can put each stock into corresponding portfolios. Thereafter, it will come to 5×5=25 portfolios. The portfolios are updated at the beginning of each year. Each portfolio will be translated into an index formed by value-weighted method.
Among all of the stocks available, the ones that are special treated or named with “*ST”, “S*ST”, “S”, “ST” and “SST” are eliminated because there are some problems with their financial condition. Furthermore, the stocks with negative BE/ME are also excluded. Finally, consistent with Fama and French [8], we exclude the financial firms in the samples because of their high leverage ratio.
There are two methodologies which are widely used to test the explaining factors of stock returns. One is univariate sorting test, the other one is univariate and multivariate cross-sectional regressions. Furthermore, there are two statistical methods to test whether adding an IPO portfolio can expand the mean-variance frontier generated by the benchmark portfolios: mean-variance spanning test and meanvariance step-down test. Before introducing the two methods, we have to clarify some conceptions as below:
1) Augmented assets: the union of both new assets (IPO portfolio) and benchmark assets 2) Spanning: the mean-variance frontier of the benchmark assets coincides with that of the augmented assets, and then there is spanning.
Univariate sorting test
At the beginning of each year, all of the stocks which meet our requirement above are classified into ten portfolios from low to high according to their beta, ME, BE/ME, liquidity, positive E/P, C/P and D/P respectively based on tenths of the value of factors mentioned above. To test the influence of negative E/P, C/P and zero D/P on the stocks returns independently, three additional portfolios are formed, which contains the stocks with negative E/P, C/P and zero D/P respectively. Therefore, there are eleven portfolios for E/P, C/P and D/P respectively. At the beginning of next year, all stocks are reclassified into new portfolios including new stocks which meet our requirement and will be held for a whole year. To get the yearly return of each portfolio, we average each single stock’s monthly returns of the whole year, and calculate the equal-weighted mean of the average monthly returns of all the stocks in every portfolio. Additionally, to avoid the influence of the outliers, the smallest and largest 1% of the observations of the monthly returns and all the explanatory factors are set to be the second smallest and largest respectively as Fama and French have done in 1992 [7]. Through this method, we can intuitively find whether stock returns have positive or negative relationship with all of the explanatory factors respectively. Finally, we find the relationships among(between) stock returns and all the explanatory factors respectively. If there is a single factor significantly related with stock returns, it is considered to be the only significant factor. If there are two factors significantly related with the stock returns, we firstly classify all the stocks into five portfolios according to one factor, and then subdivide each portfolio into five portfolios based on the other factor. Therefore, there are totally twentyfive portfolios. This “subdivide” method is used to control one factor when testing the relationship between the other factor and stock returns. If there are three, four or even more significant factors, the same method above can also be used.
Univariate and multivariate cross-sectional regressions
For univariate regression, all of the stock returns are regressed on each factor in cross-section, and then the monthly coefficients and t-statistics are averaged. In addition, three dummy variables for negative E/P, C/P, and zero D/P are constructed in order to test the relationship between negative E/P, C/P, zero D/P and the stocks returns independently, The average monthly t-statistic can distinguish the significant explanatory factors. The key point is that the monthly coefficient and t-statistic are positive or negative alternatively at the same time. So the positive (negative) t-statistic stands for positive (negative) relationship between stock returns and factors. If the average of the monthly t-statistic exceeds 1.96 (or less than -1.96), it means that the factor can significantly explain the stock returns. Similar with the univariate sorting method, the stock returns is regressed on the factors significant in the multivariate regression, which can help us to find out the intrinsic influence of each factor on the stock returns when controlling the other factors. Different from Fama and French [14], not all of the factors are included in the same regression because the insignificant factors may affect the explanatory power of the significant factors.
Mean-variance spanning
This method statistically tests the ability of the new assets to improve the investment opportunity set of benchmark assets. Suppose that there are K benchmark portfolios and one IPO portfolio whose returns are R1t and R2t respectively, where R1t is a K×1 vector and R2t is a scalar. Using the ordinary least squares approach, we estimate the model as below:
R2t = α + βR1t + ξt, t = 1,2,….T
Where β is a 1×K vector and R1t is a K×1 vector, R2t and α are scalars. The null hypothesis of spanning is:
H0:α=0, δ=1-β1k=0
Where 1k is a K×1 vector whose elements are all ones. We can then calculate the Wald test statistic as:
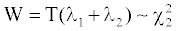
Where λ1 and λ2 are the two eigen vectors of the matrix 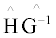
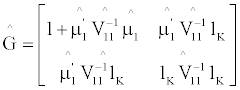 and
and
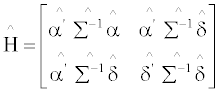
If we fail to reject the null hypothesis, then there exists spanning between the mean-variance frontiers of benchmark portfolios and the augment portfolios (benchmark portfolios plus an IPO portfolio). Conversely, if we succeed to reject the null hypothesis, it proves that adding the IPO portfolio can expand the mean-variance frontier generated by benchmark portfolios thus improve the investment opportunity sets.
To understand why failing to reject the null hypothesis implies mean-variance spanning, we can see that when it happens, for every IPO portfolio, we can find a portfolio of the K benchmark portfolios that have the same mean with the IPO portfolio (since α=0, β1k =1 and E[ξt]=0) but lower variance than the IPO portfolio (since R1t and ξt are uncorrelated and Var[ξt] is positive definite). Therefore, there always exist a group of benchmark portfolios that dominate the IPO portfolio.
In terms of geometry, we can divide the mean-variance spanning test into two segments: Global Minimum Variance (GMV) portfolio and Tangency portfolio. To be specific, the Wald statistic can be rewritten as below:
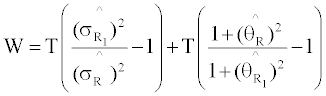
Where 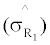 and
and 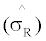 denote the standard deviation of the GMV portfolio of benchmark assets and augmented assets respectively,
denote the standard deviation of the GMV portfolio of benchmark assets and augmented assets respectively, 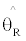 and
and 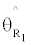 are the slope of lines which have the tangency with augmented assets and benchmark assets from original point respectively. The first term measures the change of the GMV portfolios as a result of the addition of an IPO portfolio. The second term measures whether there is improvement in the squared tangency slope when adding an IPO portfolio on the set of benchmark portfolios. Similarly, sharp ratio is used to measure the improvement in tangency slope.
are the slope of lines which have the tangency with augmented assets and benchmark assets from original point respectively. The first term measures the change of the GMV portfolios as a result of the addition of an IPO portfolio. The second term measures whether there is improvement in the squared tangency slope when adding an IPO portfolio on the set of benchmark portfolios. Similarly, sharp ratio is used to measure the improvement in tangency slope.
Step-down procedure
As illustrated before, we project R2t on R1t and estimate the following model:
R2t= α + βR1t + ξt, t = 1,2,….T
Where R1t is a K-vector of returns on the K benchmark portfolios and R2t is a scale of return on the IPO portfolio. E[ξt] = 0 and 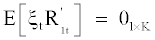 , where 01×K is a horizontal vector of zeros.
, where 01×K is a horizontal vector of zeros.
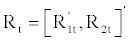 is defined as the raw returns on the 1+K portfolios at time t. Their expected returns are written as
is defined as the raw returns on the 1+K portfolios at time t. Their expected returns are written as 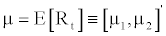 and the covariance matrix of the 1+K portfolios follows as:
and the covariance matrix of the 1+K portfolios follows as:
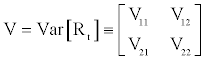
We have provided the necessary and sufficient conditions for spanning in terms of restrictions on α and δ as:
H0 : α = 0, δ = 1-β1k = 0
Where α = 0 and δ = 1-β1k = 0 are for testing whether the two tangency portfolios and GMV portfolios are statistically different respectively.
To prove it, we consider two portfolios on the mean-variance frontier of the 1+K portfolios assets with their weights as followed:
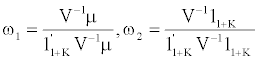
From Merton (1972) and Roll (1977), we know that ω1 is the weight of tangency portfolio while the tangent line starts from the origin, ω2 and is the weight of Global Minimum Variance portfolio.
Denote 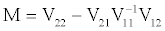 and
and 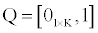 where 01×K is a horizontal K-vector with its elements all zeros. Using the partitioned matrix inverse formula, we can get the tested IPO portfolio in these two portfolios with their weights as below:
where 01×K is a horizontal K-vector with its elements all zeros. Using the partitioned matrix inverse formula, we can get the tested IPO portfolio in these two portfolios with their weights as below:
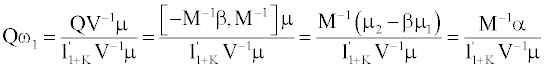
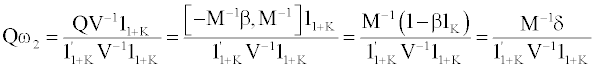
From the equation above, we can see that α = 0 and δ = 1–β1k = 0 are for testing whether the IPO portfolio has zero weights in the Tangency portfolio and Global Minimum Variance (GMV) portfolio. When there are two different mean-variance portfolios in which the IPO portfolio has zero weights, according to the two-fund separation theorem, every portfolio in the mean-variance frontier of 1+K portfolios has its IPO portfolio with weight of zero.
Factors to form benchmark portfolios
Firstly we use the univariate sorting methodology to find the factor (s) that can significantly influence the cross-sectional variation in average monthly returns. Tables 1 and 2 show the equal-weighted average returns of portfolios formed on liquidity (turnover rate) and Ln(BE/ME). They show that liquidity and Ln(BE/ME) have significant relationship with stock returns, both in the test of each year and average of each year. With respect to liquidity, it shows that the returns of portfolios have a strictly positive relationship with the liquidity (turnover rate). For Ln(BE/ME), it has the opposite trend with stock returns except for one outlier which belongs to portfolio 10. Liquidity test without any outlier illustrates that it has stronger power in explaining the stock returns than Ln(BE/ME). Furthermore, we investigate the interaction between liquidity and Ln(BE/ME). The main intention of our method is to control one variable when testing the other variables. To be specific, all of the stocks are firstly classified into 5 portfolios every year based on their value of liquidity, and then each “liquidity” portfolio are subdivided into 5 portfolios based on their value of Ln(BE/ME). Liquidity is controlled, which can be seen in the right side of the table 3. The same process can be run by reversing the order of liquidity and Ln(BE/ME) and the same effect also can be found in the right side of Table 4. We find a general positive, negative relationship between stock returns and liquidity, Ln(BE/ ME) respectively from Table 3 and 4. However, the liquidity is more significant than the Ln(BE/ME), which is consistent with the outcome of our regression method below.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1999 | 0.3 | 1.3 | 2.0 | 2.7 | 3.0 | 2.6 | 4.2 | 5.1 | 2.5 | 5.6 |
| 2000 | 3.3 | 4.5 | 3.8 | 4.7 | 4.9 | 5.3 | 5.8 | 6.4 | 6.5 | 6.8 |
| 2001 | -2.4 | -2.1 | -2.0 | -1.6 | -1.6 | -1.0 | -0.3 | -1.9 | -1.7 | -0.8 |
| 2002 | -1.7 | -1.5 | -1.5 | -1.6 | -1.5 | -1.3 | -0.4 | -1.8 | -2.8 | -0.1 |
| 2003 | -1.4 | -1.2 | -0.7 | -0.8 | -0.4 | -1.1 | 0.2 | -1.8 | 1.8 | 0.9 |
| 2004 | -1.3 | -1.0 | -1.0 | -0.4 | -0.7 | -1.0 | -1.9 | -0.6 | -0.5 | -1.1 |
| 2005 | -0.9 | -0.6 | -0.9 | -0.5 | -1.0 | 0.0 | -0.2 | -2.4 | -1.0 | -2.8 |
| 2006 | 6.2 | 6.2 | 5.5 | 5.8 | 6.0 | 6.3 | 6.5 | 6.5 | 8.1 | 7.9 |
| 2007 | 11.1 | 8.9 | 10.5 | 11.1 | 10.4 | 11.4 | 11.4 | 12.4 | 12.5 | 14.5 |
| 2008 | -5.5 | -6.4 | -6.3 | -5.7 | -5.2 | -4.2 | -3.8 | -4.2 | -3.0 | 1.1 |
| 2009 | 6.0 | 7.3 | 8.0 | 8.4 | 8.9 | 8.7 | 8.6 | 9.6 | 9.2 | 10.9 |
| 2010 | 0.1 | 0.2 | 1.1 | 1.4 | 1.9 | 2.6 | 1.9 | 5.7 | 3.9 | 4.4 |
| Average | 1.2 | 1.3 | 1.5 | 1.9 | 2.1 | 2.3 | 2.7 | 2.7 | 2.9 | 3.9 |
Table 1: Returns of Portfolios Formed on Liquidity.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1999 | 2.4 | 0.6 | 2.3 | 2.3 | 2.3 | 1.9 | 2.4 | 2.2 | 1.9 | 2.9 |
| 2000 | 6.1 | 6.2 | 5.9 | 5.0 | 4.6 | 4.8 | 4.7 | 4.4 | 3.9 | 4.4 |
| 2001 | -1.1 | -1.5 | -2.0 | -1.9 | -1.9 | -1.9 | -1.8 | -1.6 | -1.7 | -1.4 |
| 2002 | -1.3 | -1.7 | -1.5 | -1.5 | -1.6 | -1.7 | -1.6 | -1.5 | -1.2 | -1.5 |
| 2003 | -1.1 | -2.4 | -1.8 | -1.6 | -1.4 | -0.9 | -0.4 | -0.3 | -0.6 | 0.2 |
| 2004 | -2.0 | -1.6 | -1.9 | -1.0 | -1.0 | -1.0 | -0.1 | -0.5 | -0.4 | 0.1 |
| 2005 | -0.8 | 0.5 | 0.2 | -0.4 | -0.7 | -0.9 | -1.0 | -0.6 | -0.2 | -0.4 |
| 2006 | 4.9 | 8.0 | 7.1 | 6.9 | 5.8 | 5.7 | 6.1 | 6.5 | 5.9 | 6.7 |
| 2007 | 13.4 | 14.1 | 11.3 | 11.8 | 11.0 | 11.4 | 10.9 | 10.8 | 10.9 | 10.8 |
| 2008 | -4.1 | -4.6 | -5.4 | -5.4 | -6.1 | -5.7 | -6.2 | -6.6 | -6.3 | -6.1 |
| 2009 | 9.8 | 8.3 | 9.0 | 8.5 | 8.7 | 8.3 | 8.3 | 7.8 | 8.6 | 8.1 |
| 2010 | 3.2 | 2.4 | 3.1 | 1.7 | 2.1 | 1.1 | 0.4 | -0.3 | -0.9 | -0.9 |
| Average | 2.5 | 2.3 | 2.2 | 2.0 | 1.8 | 1.8 | 1.7 | 1.7 | 1.7 | 1.9 |
Table 2: Returns of Portfolios Formed on Ln(BE/ME).
| Returns | Liquidity (Turnover Rate) | Liquidity | Liquidity (Turnover Rate) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||||
| Ln(BE/ME) | 1 | 2.2 | 2.6 | 2.3 | 2.9 | 3.1 | Ln(BE/ME) | 1 | 18.4 | 36.6 | 56.5 | 75.6 | 98.3 |
| 2 | 2 | 1.9 | 2.2 | 2.6 | 3.8 | 2 | 20.2 | 37.4 | 56.5 | 76.1 | 99.1 | ||
| 3 | 1.1 | 1.6 | 2.1 | 2.4 | 3.9 | 3 | 20.7 | 37.3 | 56.1 | 76 | 96.8 | ||
| 4 | 1 | 1.8 | 2.3 | 3.1 | 3.8 | 4 | 20.4 | 36.8 | 55.5 | 75 | 96.5 | ||
| 5 | 1.2 | 1.8 | 2.7 | 2.8 | 3.6 | 5 | 20.2 | 36.3 | 56.3 | 74.1 | 95.3 | ||
Table 3: Returns of Portfolios First Sorted on Liquidity and Subdivided on Ln(BE/ME).
| Returns | Liquidity (Turnover Rate) | Ln(BE/ME) | Liquidity (Turnover Rate) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | ||||
| Ln(BE/ME) | 1 | 2.3 | 3 | 1.9 | 2.3 | 1.9 | Ln(BE/ME) | 1 | -2.3 | -2.3 | -2.2 | -2.3 | -2.2 |
| 2 | 1.9 | 2 | 2.2 | 2.4 | 2.8 | 2 | -1.4 | -1.4 | -1.4 | -1.5 | -1.5 | ||
| 3 | 1.1 | 1.7 | 2.1 | 2.3 | 3.7 | 3 | -0.7 | -0.7 | -0.8 | -0.8 | -0.8 | ||
| 4 | 1 | 1.6 | 2 | 2.6 | 3.6 | 4 | -0.1 | -0.1 | -0.1 | -0.1 | -0.1 | ||
| 5 | 1.1 | 1.6 | 1.7 | 2.4 | 2.7 | 5 | 0.7 | 0.6 | 0.6 | 0.7 | 0.6 | ||
Table 4: Returns of Portfolios First sorted on Ln(BE/ME) and Subdivided on Liquidity.
Additionally, we also use the univariate and multivariate crosssectional regressions methodology. We firstly test the stability of each variable by unit root test. The results show that all the p-values of each test is nearly zero, which suggest that each time series of variables included in the regressions is stable. Table 5 shows the coefficient and t-statistic of the factor included in the univariate and multivariate regressions. The univariate regression demonstrates that there are only two factors significantly explaining the stock returns with 5% significant level, liquidity and Ln(BE/ME). The coefficients of liquidity and Ln(BE/ME) are positive and negative respectively. To investigating the interaction in pairs, we include them into the same regression, and find that liquidity still has strong power to explain the stock returns, which is the same with that in univariate regression. However, Ln(BE/ ME) fails to explain the stock return and its validity is absorbed by liquidity. Even so, we still form benchmark portfolios according to liquidity and BE/ME (Tables 6 and 7).
| Model | Intercept | BETA | Liquidity | Ln(ME) | Ln(BE/ME) | E(+)/P | E/P dummy | C(+)/P | C/P dummy | D(+)/P | D/P dummy |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.486 | -0.609 | |||||||||
| 0.696 | -0.319 | ||||||||||
| 2 | -1.899 | 0.099 | |||||||||
| -6.514 | 8.297*** | ||||||||||
| 3 | -3.214 | 0.372 | |||||||||
| -1.209 | 1.051 | ||||||||||
| 4 | 0.839 | -1.163 | |||||||||
| -1.046 | (-2.102)** | ||||||||||
| 5 | 1.927 | -0.319 | -0.085 | ||||||||
| 1.836 | -0.394 | -0.118 | |||||||||
| 6 | 2.101 | -0.502 | -0.351 | ||||||||
| 1.776 | -0.497 | -0.497 | |||||||||
| 7 | 1.89 | -0.679 | -0.039 | ||||||||
| 1.173 | -0.303 | -0.146 | |||||||||
| 8 | -2.502 | 0.099 | -0.665 | ||||||||
| -6.595 | 8.099*** | -1.018 |
* Significance at 10% level ** Significance at 5% level *** Significance at 1% level
Table 5: Univariate and Multivariate Cross-sectional Regressions from 1999 to 2010.
| 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Medicine | 3.0 | 3.3 | -2.1 | -1.5 | -0.7 | -0.7 | ||||||
| Information | 2.4 | 1.6 | -3.6 | -2.7 | -0.3 | -1.3 | ||||||
| Food | 2.4 | 2.9 | -1.8 | -1.9 | -3.3 | -3.4 | ||||||
| Chemical | 0.8 | 4.0 | -0.8 | -2.1 | -0.9 | -0.1 | ||||||
| Metal | 3.6 | 5.8 | -1.7 | -2.3 | 0.4 | -1.8 | ||||||
| Transportation | 3.7 | 5.1 | -0.8 | 0.3 | 0.3 | -2.3 | ||||||
| Mechanical | 2.0 | 4.2 | -0.8 | -2.9 | -0.3 | -2.7 | ||||||
| Rag trade | 3.5 | 6.7 | -1.6 | -1.3 | -3.5 | -2.0 | ||||||
| Realty | 0.9 | 5.0 | -2.4 | -2.9 | -4.1 | -3.2 | ||||||
| Overall | 2.3 | 4.2 | -1.5 | -2.2 | -0.6 | -1.7 | -1.4 | 11.1 | 8.6 | -6.7 | 4.4 | -0.6 |
Table 6: Returns of IPO equal-weighted portfolios.
| 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Medicine | 3.4 | 2.7 | -2.3 | -1.1 | -0.7 | -0.9 | ||||||
| Information | 3.0 | 2.4 | -2.9 | -3.1 | 2.6 | -0.9 | ||||||
| Food | 2.5 | 3.3 | -1.4 | -2.2 | -1.9 | -3.3 | ||||||
| Chemical | 1.3 | 4.2 | -1.1 | -1.7 | -1.2 | 0.3 | ||||||
| Metal | 4.8 | 7.2 | -2.2 | -1.5 | 1.0 | -1.7 | ||||||
| Transportation | 3.4 | 5.7 | 0.4 | 1.7 | 2.7 | -2.1 | ||||||
| Mechanical | 1.8 | 4.7 | -1.2 | -2.7 | -0.5 | -3.2 | ||||||
| Rag trade | 4.2 | 7.4 | -2.0 | -1.2 | -4.0 | -2.1 | ||||||
| Realty | 0.0 | 6.6 | -2.7 | -2.3 | -4.4 | -3.2 | ||||||
| Overall | 2.9 | 5.4 | -1.4 | -0.8 | 2.3 | -1.3 | -2.2 | 12.8 | 11.9 | -7.1 | 4.2 | 0.0 |
Table 7: Returns of IPO value-weighted portfolios.
Can IPO portfolios improve the investment opportunity set?
Table 8 shows the p-value of spanning and step-down test when testing all kinds of IPO portfolios’ short-run (one-year) performance to expand the mean-variance frontier. It demonstrates that only industrial IPO portfolios of medicine industry can statistically improve the investment opportunity set through the global minimum variance (GMV) portfolio no matter equal-weighted or value-weighted. Consistent with table 8, figure 1 shows the significant outcome of adding different IPO portfolio to the benchmark portfolios graphically.
| IPO Index one-year | Wald Test (p-Value) | Wald Step-1 Test (p-Value) | Wald Step-2 Test (p-Value) | |||
|---|---|---|---|---|---|---|
| H0 : α = 0, δ = 0 | H0 : α = 0 | H0 : δ = 0, when α = 0 | ||||
| Equal-Weighted | Value-Weighted | Equal-Weighted | Value-Weighted | Equal-Weighted | Value-Weighted | |
| Realty | 0.881 | 0.336 | 0.666 | 0.896 | 0.910 | 0.152 |
| Rag Trade | 0.724 | 0.845 | 0.757 | 0.867 | 0.542 | 0.633 |
| Mechanical | 0.956 | 0.875 | 0.787 | 0.850 | 0.842 | 0.690 |
| Transportation | 0.699 | 0.646 | 0.726 | 0.539 | 0.532 | 0.629 |
| Metal | 0.199 | 0.170 | 0.613 | 0.778 | 0.136 | 0.157 |
| Chemical | 0.290 | 0.521 | 0.131 | 0.285 | 0.386 | 0.966 |
| Food | 0.618 | 0.575 | 0.238 | 0.315 | 0.493 | 0.229 |
| Information | 0.225 | 0.277 | 0.612 | 0.580 | 0.086* | 0.096* |
| Medicine | 0.072* | 0.207 | 0.880 | 0.660 | 0.027** | 0.078* |
| First 6-year | 0.999 | 0.753 | 0.978 | 0.656 | 0.973 | 0.477 |
| Second 6-year | 0.357 | 0.646 | 0.222 | 0.363 | 0.400 | 0.906 |
| Whole 12-year | 0.154 | 0.449 | 0.218 | 0.400 | 0.116 | 0.506 |
Table 8: P-Value of One-Year Spanning and Step-Down Tests.
Table 9 shows the p-value of spanning and step-down test when testing all kinds of IPO portfolios’ long-run (two-year) performance to expand the mean-variance frontier. It demonstrates that IPO portfolios of all of the IPOs covering 12 years, rag trade, transportation industry and metal industry can statistically improve the investment opportunity sets mainly through the Global Minimum Variance (GMV) portfolio. However, in terms of Sharp Ratio through figure 2, only industrial IPO portfolios with transportation can significantly increase the investment opportunities. The outcome suggests that in the long run, with higher expected returns and lower variance, IPO portfolios outperforms that in short run. Consistent with table 9 and figure 2 shows the outcome of adding different industrial IPO portfolios to the benchmark portfolios graphically. Table 10 shows the mean and standard deviation of assets before and after adding the IPO portfolio on the benchmark portfolios. It suggests that no matter formed by equal-weighted or value-weighted method, industrial IPO portfolios with rag trade makes the most significant change in standard deviation of GMV portfolio and also has the most proportion of the augment assets.
| IPO Index one-year | Wald Test (p-Value) | Wald Step-1 Test (p-Value) | Wald Step-2 Test (p-Value) | |||
|---|---|---|---|---|---|---|
| H0 : α = 0, δ = 0 | H0 : α = 0 | H0 : δ = 0, when α = 0 | ||||
| Equal-Weighted | Value-Weighted | Equal-Weighted | Value-Weighted | Equal-Weighted | Value-Weighted | |
| Realty | 0.197 | 0.126 | 0.313 | 0.175 | 0.258 | 0.110 |
| Rag Trade | 0.038** | 0.061* | 0.346 | 0.367 | 0.011* | 0.019* |
| Mechanical | 0.786 | 0.449 | 0.490 | 0.293 | 0.830 | 0.730 |
| Transportation | 0.011** | 0.002*** | 0.276 | 0.097* | 0.017* | 0.009* |
| Metal | 0.071* | 0.012** | 0.732 | 0.559 | 0.024* | 0.003* |
| Chemical | 0.434 | 0.228 | 0.232 | 0.154 | 0.930 | 0.552 |
| Food | 0.720 | 0.699 | 0.680 | 0.636 | 0.432 | 0.419 |
| Information | 0.935 | 0.396 | 0.750 | 0.299 | 0.790 | 0.250 |
| Medicine | 0.368 | 0.532 | 0.644 | 0.551 | 0.295 | 0.324 |
| First 6-year | 0.829 | 0.905 | 0.690 | 0.832 | 0.746 | 0.789 |
| Second 6-year | 0.226 | 0.827 | 0.507 | 0.870 | 0.112 | 0.559 |
| Whole 12-year | 0.098* | 0.014** | 0.454 | 0.470 | 0.087* | 0.012** |
Table 9: P-Value of Two-Year Spanning and Step-Down Tests.
| Period | IPO Index | Adding IPO | Equal-Weighted | Value-Weighted | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Standard Deviation | Change in SD (%) | Propotion of IPO (%) | Mean | Standard Deviation | Change in SD (%) | Propotion of IPO (%) | |||
| One Year | Information | Before | 0.8 | 6.43 | 0.59 | 13.36 | 0.8 | 6.43 | 0.45 | 11.49 |
| After | 0.6 | 6.39 | 0.7 | 6.4 | ||||||
| Medicine | Before | 0.8 | 6.43 | 0.9 | 21.16 | 0.8 | 6.43 | 0.53 | 16.04 | |
| After | 0.7 | 6.37 | 0.7 | 6.39 | ||||||
| Two Year | Rag Trade | Before | 0.8 | 6.43 | 4.35 | 55.95 | 0.8 | 6.43 | 2.44 | 33.42 |
| After | 0.3 | 6.15 | 0.5 | 6.27 | ||||||
| Transportation | Before | 0.8 | 6.43 | 1.2 | 24.19 | 0.8 | 6.43 | 2.96 | 29.02 | |
| After | 0.9 | 6.35 | 1.2 | 6.24 | ||||||
| Metal | Before | 0.8 | 6.43 | 0.38 | 21.99 | 0.8 | 6.43 | 1.05 | 24.11 | |
| After | 0.7 | 6.4 | 0.9 | 6.36 | ||||||
| Whole 12-year | Before | 1.7 | 8.61 | 0.34 | 16.02 | 1.7 | 8.61 | 0.12 | 7.44 | |
| After | 1.5 | 8.58 | 1.6 | 8.6 | ||||||
Table 10: Mean and Standard Deviation of Assets Before and After Adding the IPO Portfolios.
Figures 3 and 4 below prove our outcomes above directly. The lateral axis denotes the standard deviation of returns, and the vertical axis denotes the mean value of returns. Firstly, figure 3 presents the comparison between IPO portfolios and benchmark portfolios in the short and long run. As a whole, industrial IPO portfolios underperform the benchmark portfolios which stand for the market performance, except for transportation industry which is marked with a black circle. Secondly, figure 4 presents the comparison between short-run and long-run IPO portfolios performance. No matter in equal-weighted or value-weighted, IPO portfolios in the long run outperforms that in the short run. The IPO portfolios in the long run, which are marked by black circles, come with higher mean value and lower standard deviation.
All kinds of IPO portfolios’ short-run and long-run performances in expanding the mean-variance frontier have been examined by spanning and step-down approaches. We find that only industrial IPO portfolios with medicine industry have the ability to improve the investment opportunity sets in the short-run. IPO portfolios with all the IPOs covering 12 years, rag trade, transportation industry and metal industry can expand the mean-variance frontier more significantly in the long run. However, in terms of Sharp Ratio, only industrial IPO portfolios with transportation can significantly increase the investment opportunities. Additionally, our outcome suggests that with higher expected return and lower variance, IPO in the long run outperforms that in the short run.
According to Behavioral Finance, IPO’s strong long-term performance is an anomaly, i.e. Chinese investors have under-reaction to the quality information of IPO stocks. This demonstrates that Chinese capital market is inefficient. Although Chinese IPO stock has a significant problem of under pricing, its price on the first day of listing is still lower than market price. The real information of the IPO stock will emerge gradually after several years, which results in the IPO’s stronger long-term performance than stock market.
Our outcome is affirmative and important for both financial institutions and mean-variance investors. There is room for financial institutions to develop the IPO-related products with medicine industry in the short run and rag trade, transportation industry, metal industry in the long run. Also they can develop an IPO comprehensive index for long-run investment. Risk aversion Investors can gain diversification benefits from these products as well.
For the governors of Chinese stock market, we have some suggestions as below: first and foremost, they should improve the system of information announcement so as to avoid the problem of information asymmetry. Secondly, they should investigate the financial condition and background more carefully and thoroughly in order to improve the general quality of IPO firms and the efficiency of stock market to allocate the resources. Thirdly, they should administrate the intermediaries such as investment banking firm, accounting firms, and law firms more strictly to build a healthier issue environment.
This research is supported by National Natural Science Foundation of China (NSFC Grant Numbers: 71273257, 70933003, 70921061).