Journal of Developing Drugs
Open Access
ISSN: 2329-6631
ISSN: 2329-6631
Research Article - (2014) Volume 3, Issue 2
This article presents the findings from an experimental investigation assessing the role of different variables in determining electrostatic charges on a binary granular assembly in a simple hopper-chute set up. Several popular theories describing the generation and subsequent mitigation of static charges is reviewed and the experimental results are discussed in the light of those theories. A detailed discussion is provided on the significance of several variables considered important in the study performed under conditions representative of typical pharmaceutical manufacturing. A simple probability based model is presented which accounts for eventful contacts in a binary mixture. The theoretical arguments presented in the paper, backed by statistical analysis, lend insight into well-known but poorly understood phenomena. It is demonstrated that tribocharging of granular assemblies made of a single species on a given surface was observed in accordance with their work function difference. Mitigation of this generated charge increased linearly with concentration of addition of a second species before plateauing off at higher concentrations. The extent of charge reduction depends on interplay between the work function and hygroscopicity, and the number of contacts between the species involved.
<Keywords: Powder; Tribocharging; Work function; Hygroscopicity
Scientific understanding of pharmaceutical manufacturing processes has become very important in the last decade, especially considering the QBD (Quality by Design) approach by both industry and regulatory bodies in an attempt to streamline product movement from factory to the shelf without compromising on the critical quality attributes of the product. It is imperative in this view that better understanding of granular mechanics is sought considering the fact that the pharmaceutical market is dominated by solid dosage forms. However, it is not an easily achieved task because of the fundamental paucity of knowledge and understanding of powder physics. A big concern for a pharmaceutical manufacturer is content uniformity, which is very difficult to ensure given the cohesive nature and characteristically low amounts of the active drug amidst a host of other additives, which undergo a series of unit operations before being realized in a solid formulation. Several known and unknown factors affect this chain of solid manufacturing and transport, static triboelectrification being one of the most important yet poorly understood factors. Triboelectric charging is a process that occurs when two initially neutral surfaces are in contact, transfer charge, and upon separation, remain electrically charged. Pharmaceutical unit operations like pneumatic conveying, fluidization spray deposition and milling can generate 10-7 to 10-4 C/ kg of triboelectric charges [1]. Such triboelectrification often leads to poor flow and agglomeration resulting in compromised mixing and dispersal in devices like dry powder inhalers, along with storage and handling problems. The tribocharged powders are a major safety hazard as well, especially in presence of flammable gases, solvent fumes and dust [1,2] found easily in chemical and pharmaceutical factories.
However, such contact electrification is not unique to the pharmaceutical industry and has indeed been dealt by many scientists over a considerable amount of time. As might be expected, this long standing research has produced many theories- some of which have stood the test of time, but keenly contested nonetheless by believers of an alternate theoretical model. The theoretical models describing charge generation and accumulation are broadly classified into the ion transfer model, the surface state model and the two step model (electron transfer model). The reader is guided to several excellent reviews that have been published in literature outlining the essential features of these theories [3-5].
Traditionally, electron transfer due to the difference in work function of different materials has been known to drive contact electrification [6,7] and this theory works particularly well for metal– metal contacts. The electron transfer model also frequently attempts to explain tribocharging of real insulators. Measurements on different polymer-metal systems have been carried out experimentally to show dependence of charge density on known work function differences [8]. These real insulators have surface energy defects and hence presence of high-energy electrons [9,10] often characterized by an effective work function which can give a reasonable semi quantitative approximation of the triboelectrification. Most experimental and theoretical studies on triboelectrification have been carried out on toner charging, where both toner and charger are insulators. Other major theories that have been proposed are ion transfer [11,12] and selective adsorption of impurities, specifically moisture [13,14] to explain generation of static charges on powders. The role of moisture in triboelectrification of powders can be considered analogous to modifying the resistance of a RC circuit. However, the Fermi levels of the two contacting species can be modulated by adsorbed species like water. Debye length of aqueous solutions for typical pharmaceuticals is less than the thickness of adsorbed monolayer of water implying ion transport between contacting particles through a liquid water bridge [4]. Dual role of water in triboelectrification has been highlighted in literature–linearly increasing in monolayer regime [15] at low RH while dampening charges for adsorbed water thicknesses over 3 nm at high RH. It must be borne in mind that high dielectric constant of water also decreases electrostatic interactions between particles, though the dielectric constant is much lower at the interface [16].
As discussed above, tribocharging of complex granular systems is of particular concern to the heavily regulated pharmaceutical industry. In this light, the control of such triboelectrification becomes an important technological requirement. While acknowledging the relative lack of data on contact electrification especially in pharmaceutical systems, this paper intends to gain a deeper insight into the interaction of materials with an emphasis on their material and molecular properties under relevant conditions (35 ± 5% RH, 25 ± 2°C). Several binary systems are examined in a simple hopper-chute system on different surfaces. These results are explained by a probability-based model accounting for the number of eventful contacts in the light of currently existing models. Asymmetric transfer of negative species (i.e. electrons or hydroxide ions) between small and large particles has also been factored in to account for our observations.
The broad methodology and experimental set up is adopted from Sarkar et al. [17]. The experimental assembly is shown in Figure 1. Two identical hopper and chute assemblies were fabricated in either Aluminum or Polyvinyl Chloride (PVC) with the support base made of acrylic. The hopper was loaded with primary particles followed by deionization with a bench top air ionizer (3M R963 E). They were then released through a dam (1 cm opening) in the base of the hopper to flow over the chute into Faraday’s cup connected to a nano-Coloumb meter (Monroe Electronics, Model 284), in which the magnitude of accumulated charge was measured. All equipment surfaces were thoroughly cleaned using distilled water and 70% isopropyl alcohol after every run followed by drying and deionization using the air ionizer.
All experiments were done in triplicate at ambient temperature (25 ± 2°C) and humidity (35 ± 5% RH) with the chute inclined at an angle of 30°C with respect to the horizontal which represented optimum conditions (for 30 g of primary particles) for surface contact and flow of particles. For charge reduction studies, the additives and particles were layered over each other. Homogenous discharge of material from such a layered mixture has been documented previously [17]. The previous work dealt with some commonly found second components but the current article investigates some pharmaceutical excipients as the second component.
Particle characterization for surface purity, surface area and moisture content were done using XPS (ESCALAB MKII) (Table 1), BET (NOVA Quantachrome 1000) (Table 2) and TGA (TA Q500) respectively. Work functions of the different materials involved were determined using molecular mechanics software, MOPAC 2009, starting from molecular structures at equilibrium geometry generated with AVOGADRO 1.0.3 with Restricted Hartree Fock (RHF) PM3 methodology, as outlined by Mazumder et al. [18] Table 3 enlists the properties of different materials used in the study. The authors acknowledge that the value of PVC is over predicted, most likely due to a computational limitation in capturing the chain length as discussed previously [17]. However, our assessment should not be qualitatively affected as PVC is known to have the highest work function amongst all materials assessed in this study. Variables of study include primary particle type (Lactose non-pareils (NP), glass beads (GB)), equipment surface (Aluminum, PVC), nature (sodium stearate, sodium bicarbonate and stearic acid) and concentration of additives (0-15% w/w), and angle of inclination of chute (15-60°C). Percentage charge reduction values (%CR) were plotted for different particle surface combinations at different additive concentrations and chute inclines.
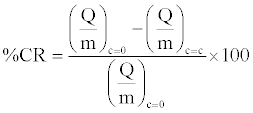 (1)
(1)
| Additive | C | O | Na |
|---|---|---|---|
| Sodium Bicarbonate | 56.40 | 33.56 | 10.05 |
| Stearic Acid | 86.83 | 13.17 | - |
| Sodium Stearate | 85.43 | 9.49 | 4.49 |
Purity and elemental composition of the additive samples was determined using XPS (ESCALAB MKII) with a focused monochromatic Al K α source. No other element was found indicating sample purity and freedom from adventitious contamination
Table 1: XPS data showing normalized elemental percentage compositions used for the different additives under consideration.
| Additive | Specific Surface Area (m2/g) | Moisture Content at 35% RH at 25° C (%w/w) |
|---|---|---|
| Stearic Acid | 3.26 | 0.06 |
| Sodium Stearate | 3.74 | 1.08 |
| Sodium Bicarbonate | 1.15 | 0.3 |
Specific surface area was measured using BET method in a NOVA Quantachrome 1000 Analyser. Moisture content was determined using Thermo gravimetric Analysis (TA Q500) after equilibriating at 35% RH at 25°C.
Table 2: Experimentally determined properties of different additives used for studying charge reduction on different particle-surface systems.
| Additives | Sodium Stearate | Sodium Bicarbonate | Aluminium | Glass | Stearic Acid | Lactose | Polyvinyl Chloride (PVC) |
|---|---|---|---|---|---|---|---|
| Calculated Work Function (eV) | 4.22 | 4.46 | 4.53 | 5.32 | 5.5 | 5.85 | 7.36 |
Work function of the additives were determined using MOPAC2009 from structures generated with AVOGADRO 1.0.3 with Restricted Hartree Fock (RHF) PM3 methodology. The unit of Work Function is Electron volts (eV).
Table 3: Calculated work functions of materials used to study tribocharging and subsequent charge reductions in granular flows.
The % CR values reflect the percentage reduction in charge to mass ratio on the overall granular assembly when an excipient was added at a concentration c at a fixed chute inclination (30°C). Similarly, %CR was calculated as angle was varied for fixed concentration (5% w/w). The statistical significance of the data was tested using dummy variable analysis [19] for different surfaces, additives, concentration of additives and standard deviation within experimental runs as inputs affecting the percentage charge reduction. The references for the statistical analysis were aluminum (surface), NP (particles), stearic acid (additive), 15° (angle) and 0% w/w additive (concentration). All the statistical tests were done in MS EXCEL. The charge reduction studies were done under the previously identified optimum conditions [17], i.e. 30°C chute angle and a mass loading of 30 g of 1 mm size primary particles. The effect of variation of chute angle was done with a constant additive concentration of 5% w/w.
Model for predicting number of contacts and subsequent tribocharging
A rigorous analysis of the overall triboelectrification of a system can be undertaken only after a precise knowledge of the number of particle-particle and particle-surface contacts taking place is obtained. However, it is an extremely complicated mathematical task in 3 dimensions, especially for different type of particles and surfaces. This analysis has been simplified by placing different types of elements (particles and surfaces) in a random linear assembly. This arrangement, though highly simplified, can be considered reasonable given that sliding is the dominant mode of charge transfer as determined in previous experimental studies [1,20]. It is assumed that if a particle is charged at a point, the effective work function at other points on the particle surface does not change much. This approximation is also supported by the fact that our particles are dielectric in nature and local charge density at one point does not appreciably influence contacts at other points.
Bearing the above approximations, two types of particles denoted by red (R) and green (G) particles are assumed. The inert elements are denoted by W. The inert elements could be representative of particles that have already been saturated with charge exchange and can accommodate no more charge. When R and G come in contact, based on difference in work function (ϕR<ϕG) so that on a single collision between R and G, the following electron exchange takes place:
R→ R+
G→G−
R-R and G-G collisions do not yield any charge transfer as there is no work function differential. Two cases are considered which are aimed at qualitatively validating the proposed model.
Inert surface: When G or R comes in contact with W, the charges are damped. When R+ comes in contact with surface R+ + S → R + S (R loses charge).
When G- comes in contact with surface G− + S →G + S (G loses charge).
The overall triboelectrification is envisaged to be completed in two steps:
Step 1: When R is added to G, some R and G particles come in contact and get charge.
Step 2: Some of the particles come in contact with surface and become neutral again. However if R ≠ G, this results in some residual charge that is measured.
Analysis estimating amount of charge generated
The charge is proportional to the number of R and S particles that touch each other.
The number of adjacent R and G gives a measure of the total charge generated.
The probability that the ith particle is R is given by 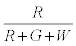
Similarly, the probability that the i+1th particle is G is given by 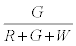
Therefore expected number of contacts between R & G is given by
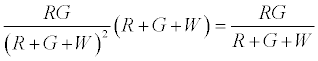
Thus after step 1, the system has 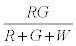 positively charged R particles and
positively charged R particles and 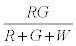 negatively charged G particles.
negatively charged G particles.
Step 2- Estimating charge lost to surface
It is assumed that all the charge on the red particles get evenly distributed i.e. any red particle is equally likely to be charged. The same consideration holds for the green particles. Now let us estimate fraction of red particles that do not touch the surface.
By similar calculations as before this is proportional to
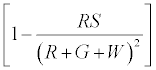
Therefore charge left on 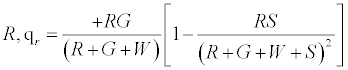 (2)
(2)
And, charge left on 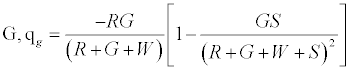 (3)
(3)
Total charge, 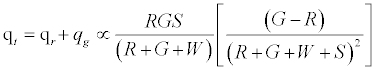 (4)
(4)
Given identical number of red and green particles, it can be seen that the net charge would be 0; as can be expected from such a set up. Figure 2a predicts linear effect of work function difference on the net charge/mass. Increasing particle concentration is expected to increase net charge/mass up to a point after which it plateaus off (Figure 2b). As the chute angle increases, the number of contacting particles can be expected to decrease and thereby decrease the net charge on the granular assembly.
The most electronegative surface: The surface is considered to be most electronegative in this case such that
• R particles
The number of R particles that are left positively charged after the first contact with green particles is given by 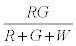
The fraction of particles that remain neutral after the first contact are given by
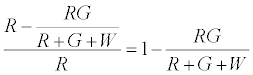
The number of R particles left uncharged after the first contact is given by 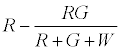
The fraction of particles that touch the surface are given by 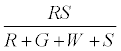
The numbers of neutral R’s that go to R+ are given by 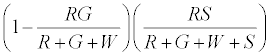
The positively charged R particles stay positively charged, while the neutral R’s become positive on contact with the surface. Thus the total charge on red particles (qr) is given by
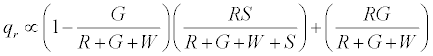 (5)
(5)
Under a monolayer regime, where all particles would touch the surface i.e. S goes to ∞ , it can be easily shown that the above expression reduces to R implying all red particles getting a positive charge .Under the limiting condition of excess inert particles which could be realized in situations like excessive humidity, the above expression simplifies to 0.
• G Particles
The negative charge on green particles on first contact with red particles is given by 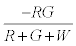 . The number of green particles touching the surface is given by
. The number of green particles touching the surface is given by 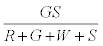 . It is assumed that the surface being strongly electronegative, any negatively charged green particle that touches the surface would lose the charge and eventually become positively charged. Thus the total negative charge lost by green particles would be given by
. It is assumed that the surface being strongly electronegative, any negatively charged green particle that touches the surface would lose the charge and eventually become positively charged. Thus the total negative charge lost by green particles would be given by 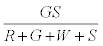 . The total charge on green particles (qg) is given by
. The total charge on green particles (qg) is given by
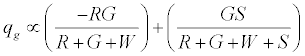
On applying the limiting condition of S →∞ , the charge on green particles would be less than G. When W → ∞ , the expected result of qg → 0 is recovered. The total charge on the granular assembly would thus be given by:
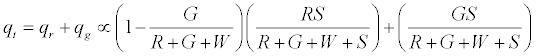
A similar analysis could be used for the most electropositive surface, or any order of work function of the different materials involved. It can be seen that increase of inert W particles would decrease the overall charge. If however, negatively charged spheres, which can happen due to selective adsorption of hydroxide ions, replaced the W particles there would be a further reduction in the overall positive charge. In case of electropositive surface, addition of negatively charged spheres would have lesser of an effect in determining the overall charge. Model predictions on the effect of additive on net charge/mass are displayed in Figures 3a-3d. When the primary particle charges positively with the surface (Figures 3a and 3b), addition of an additive with a work function more than the surface would be the ideal charge mitigation agent while the converse is true for the cases when the particle charges negatively with respect to the surface (Figures 3c and 3d). The model also predicts that increasing the additive concentration actually skews the charge towards that of the additive. Careful attention must be given therefore to both the work function and concentration of the additive in order to reduce the net charge to a desired level. Experimental observations for binary mixtures are evaluated in the light of this simple probabilistic model by considering different number of component particles.
Tribocharging of binary mixtures
All paremeters except standard deviation in the data were concluded to exert statistically significant effect on the output variable which is percentage charge reduction.The effect of the different parameters through the P values is summarized in Table 4. The effects have been qualititively assessed in the following cases:
| Factors | P statistic |
|---|---|
| Primary Particle | 0.000331 |
| Surface | 0.024 |
| Sodium stearate | 6.68×10-5 |
| Sodium Bicarbonate | 0.00936 |
| Additive Concentration (5% w/w) | 1.42×10-5 |
| Angle | 7.2×10-6 |
| Standard Deviation | 0.0724 |
A P statistic less that 0.05 implies statistical significance at 95% level of confidence. All factors except standard deviation in the data exert statistical significance on the percentage charge reduction.
Table 4: Statistical analysis of data using dummy variable methodology.
Case I: glass beads on aluminum: The initial charge on Aluminum surface is low as can be seen from Figure 4. Sodium bicarbonate and stearic acid would be expected to acquire small positive charges on aluminum while glass beads acquire a negative charge. These additives would also be expected to render glass beads more negative in a one to one collision. But these considerations suffice only at 0% RH and the influence of ambient humidity can be gauged from the observed data. As the angle of inclination of the chute incline increases, authors predict that there should be charge reversal as more and more positively charged particles fall into the Faraday’s cup. The CR values expectedly should go over 100%. However, quite the opposite is observed as negative charge increases on the granular assembly as angle of inclination is increased. Previous research shows that hydroxide ions tend to adsorb preferentially over surfaces [15,21,22] and these would render the particles under consideration negative. No moisture adsorption was observed on NP and GB particles and thus the argument is focussed on moisture content of the additives. Stearic acid, with the least water adsorption as seen from TGA data should be negatively charged based on pure work function criteria alone. Sodium stearate has the highest moisture content while sodium bicarbonate is the intermediate case between the two. This is reflected in Figure 5 where all the additives show a negative charge at steeper chute inclines as much more negative particles fall into the Faraday’s cup. With both sodium stearate and stearic acid, the presence of positive particles controls the amount of negative charges. It must be realized that as the angle of inclination is increased, both the normal contact force and contact time decrease which lead to poorer charge development and the overall charge becomes more dependent on the adsorbed moisture.
When the chute angle was kept at 30° and the concentration was varied, increase in %CR values with concentration for all additives was observed. However, the order of charge reduction on the whole granular assembly exactly parallels the moisture content with sodium stearate proving the most effective and stearic acid being the least. These are depicted in Figure 6. The effectiveness of the cations responsible for charge mitigation is dictated by surface dissolution of the additive species and ionic diffusivities. Stearic acid has a low proton concentration due to both low moisture and limited surface dissolution as opposed to the other sodium salts.
Case II: Lactose Non Pareils on Aluminum: Similar considerations apply as in the above case as can be seen from Figure 7. Lactose NP spheres show a high negative charge on aluminum surface and would be charged more negatively in a one to one collision with all the concerned additives. It is thus expect that the CR values to be less negative in this case at higher angles of inclination. At lower angles an increase in charge reduction is observed and this trend parallels the moisture content of the additives. Sodium stearate is the most effective of the lot as the angle of the chute moves from 15 to 30°. Stearic acid is the least positively charged of all species and has the least moisture content as well and consequently affects the overall charge the least. Sodium stearate however has the maximum charge reduction till 30° and also cause the maximum amount of negative charges at steeper inclines. As regards to variation of charge reduction with concentration, a similar trend as seen in the previous case is observed and is depicted in the Figure 8. The CR values reflect the importance of sample hygroscopicity as stearic acid proves to be the most effective charge mitigation agent followed by sodium bicarbonate and stearic acid.
Case III: Glass Beads on PVC: The variation of CR with angle of inclination of the chute when glass beads flow over different surfaces is represented in Figure 9. In this case, the glass beads are positively charged due to the work function difference between GB and PVC. All the additives would also, on same logic be positively charged with sodium stearate and sodium bicarbonate being the most positive while stearic acid having a mild positive charge. Adsorption of select negatively charged species like hydroxide ion through moisture would render the additives to be negatively charged too, the amount of negative charge being related to the adsorbed moisture content as measured by TGA. This implies greater CR values as opposed to the previous cases. This is what is observed in Figure 10 with CR values paralleling the adsorbed moisture content. As mostly positive potentials would be expected from work function considerations which further favor hydroxide adsorption. The dominant nature of moisture is easily observable in the high CR values, around 200% in some cases, implying strong negative charges on particle surfaces. Along expected lines, the charge reduction is observed with increasing concentrations to be increasing and the order of charge mitigation following the same trend of the hygroscopicity as shown in Figure 10.
Case IV: Lactose Non Pareils on PVC: The considerations for NP spheres flowing over PVC are quite similar to that of the previous case (Case II). The relatively mildly positively charged NP spheres flowing with different additives, all of which would be positively charged on flowing over PVC surface and also in a single collision with a NP sphere. Stearic acid, with the least positive charge and the least moisture content would be expected to have little effect while sodium stearate has the maximum CR reading with sodium bicarbonate at an intermediate value. This is illustrated in Figure 11 where CR is plotted against chute angle and Figure 12 where CR is plotted against additive concentrations.
This work demonstrated that tribocharging in binary mixtures is a complex function of many variables. Some of these key factors include hygroscopicity, work function, flowability and contact area of the different species involved. From the results of the experimental studies, it can be concluded that mechanistic elucidation of triboelectrification cannot be achieved by solely considering work function values in a pharmaceutical process plant, but effects like adsorption and ion transport need to be accounted. The deviation from basic work function difference criteria is further enhanced as additional mechanical forces are introduced on increasing the angle. This is because contact between different surfaces is significantly reduced with an apparent increase in flowability. The final charge on the granular media is dictated by adsorbed moisture content. At lower angles, flow of typical additives is restrictive. There is typically an optimum angle, in this case at 30°, where one can see charge reduction as a mixed function of hygroscopicity and work function differences. Other mechanical properties of particulate flows become less important at higher angles with regard to overall charge on the assembly and essentially are negligible at 90°. The increase of charge reduction with increasing concentrations for all cases studied also reflects on the role of moisture content with more hygroscopic materials proving the most effective. The authors believe that determination or computation of work functions of materials after adsorbing a monolayer of moisture would be more relevant to predict tribocharging and charge mitigation under different conditions, which is the direction of future research.
Financial support is gratefully acknowledged to University of Connecticut Research Foundation. Thanks are due Dr Heng Zhang, Prof. Leon Shaw and Prof. Michael Pikal who helped with the measurements on XPS, BET and TGA. Kyeunhung Lee, Dien Nguyen, Annie King, Jin lee, Holly Grota and Apurva More are thanked for assisting with experimental measurements.