International Journal of Advancements in Technology
Open Access
ISSN: 0976-4860
ISSN: 0976-4860
Research Article - (2022)Volume 13, Issue 8
Surface water resources in Ghana have recently been overexploited owing to the resurgence of small-scale mining and other human activities that deplete these resources. These activities need discussions regarding groundwater and its optimal use. This study investigates underground dams in Ghana, especially the use of a multi-criteria decision-making procedure to help choose appropriate areas. This study outlines a number of characteristics or criteria that are unclear, confusing, or unsure in real-world circumstances. Fuzzy Analytic Hierarchy Process (AHP) is used to capture any ambiguity any criterion under consideration provides and perform pairwise matrix comparisons to select the optimal position among a collection of candidate sites. This study focuses on seven agricultural settlements in the Sunyani West area and uses a modified Fuzzy AHP approach to evaluate the options. The technique provides the best option for underground dam placement. The findings are compared to the experts’ original assessment to ensure consistency. This is done by using a detailed Fuzzy AHP approach to calculate weights depending on expert opinion and other considerations. In summary, this study uses a competent strategy to choose the optimal site for an underground dam in Ghana’s Sunyani-West Municipality.
Fuzzy Analytic Hierarchy Process (Fuzzy AHP); Multi-Criteria Decision-Making (MCDM); Triangular Fuzzy Numbers (TFN); Consistency Rate (C.R)
Pollutants from diverse sources such as home waste discharges, industrial waste disposal, mining operations, and others are progressively threatening the quality and availability of surface water resources, which serve as a key supply of water [1]. The need for fresh water supplies throughout the globe cannot be overstated. In Ghana, the expansion of small-scale and other mining operations has made most fresh water resources useless, necessitating immediate intervention [2]. Due to significant industrialization and other surface water pollution activities, ideas concerning underground dams continue to arise in Sub- Saharan Africa; nevertheless, execution is constrained by expert knowledge and procedures [3], and Ghana is no exception. Ghana has the ability to build underground dams, as shown in [4], which categorizes diverse terrain and identifies variables.
Due to the large number of aspects that must be considered, decision making in numerous areas of the economy, such as manufacturing, sales, and others, has grown more difficult. This has inspired renewed interest and development in the area of multi- criteria decision making and related methodologies [5]. Looked at the several approaches that support multi-criteria decision making when it comes to supplier assessment and selection. In multi-criteria decision making, the characteristics of the variables and data are crucial. Vagueness, ambiguity, and the unexpected nature of the situation might be tough to cope with. Various research efforts have been done to address such discrepancies in factors. The fuzzy set theory is one of the most well-known in the area of artificial intelligence, with several research applications [6]. The analytic hierarchical process, which deals with theory of measurement via pairwise comparisons and depends on expert judgments to construct priority scales to facilitate decision making is also highly useful [7].
The Sunyani West District is distinguished by a significant number of rural settlements that rely heavily on rain-fed agriculture. The district agriculture office confirms that a significant number of basic crops, mostly maize, are popular in these settlements. A number of agricultural areas have been chosen as prospective sites for the development of underground dams in order to investigate the possibilities of the Sunyani West district in the future implementation of underground dams. In this study, the elements and a well-crafted methodology are used to guide and inform the selection of the most appropriate location for the construction of underground dams.
Underground dams
A groundwater dam is a construction that prevents groundwater from flowing naturally and deposits it under the earth surface [8]. As a result, they are divided into two categories. A subsurface dam is built below ground level to prevent water from running into a natural aquifer, while a Sand Storage dam collects water in sediments [9]. Figures 1a and 1b depicts a cross-sectional view of both the sub-surface and sand-storage dams.
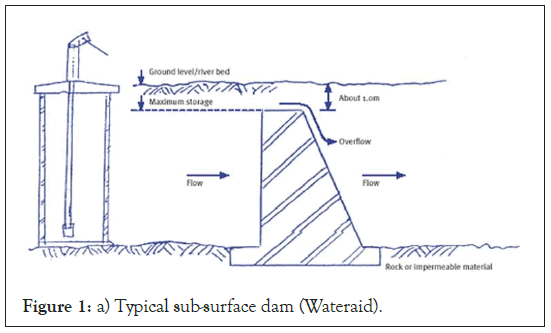
Figure 1: a) Typical sub-surface dam (Wateraid).
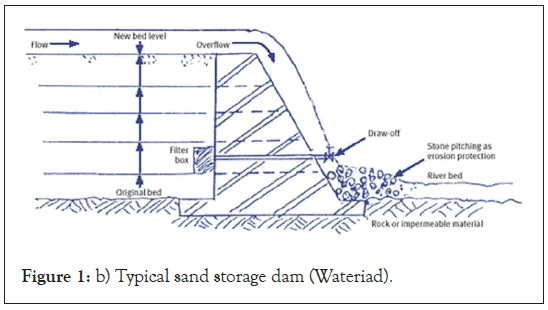
Figure 1: b) Typical sand storage dam (Wateriad).
Underground dams provide a variety of advantages, including storing seasonal water sources, preventing evaporation, reducing animal pollution, and storing water that is not suitable for mosquito development. These benefits underscore the need of considering underground dams in rising economies with rich aquifers.
Factors to consider in the construction and siting of underground dams
Various studies have attempted to determine the aspects that must be considered in the siting and building of underground dams. Absolute factors and relative factors are two types of factors. The absolute elements, with their presence or absence, have a direct impact on the site of underground dams. Topography, waterway, fault border, road boundary, and rural boundary are important absolute elements, while relative factors include permeability, hydraulic conductivity, specific yield, distance from consumption location, access to the dam site, and a variety of others [10]. It should be emphasized that relative factors are essential considerations that may or may not play a significant effect in determining these variables. However, access to the dam and distance from the consumption location were shown to be more cost-effective. Geographical maps containing this information were also gathered from a variety of sources. The potential distortion of imprecise and uncertain factors was one flaw in their analytical technique.
Application of various multi-criteria decision-making methods
Many criteria impact the selection of prospective areas for the building of underground dams. This slew of considerations makes decision-making challenging at times, especially since decision-making procedures must be rigorous and thorough. Multi-Criteria Decision-Making (MCDM) is a feasible approach that may be used in these situations. The Analytic Hierarchy Process (AHP) is a popular MCDM that has been used in a variety of applications ranging from hydrogen production to cleaning system monitoring [11]. AHP has been used in managerial fields such as water resource management to aid decision-making [12- 14]. It has been proven that the AHP considers the accumulated weight to the original aim in addition to the relative value of an element [15]. Because of the complexity and diverse interests of the operators and decision makers, making judgments in the natural environment may be exceedingly challenging.
Researchers have always utilized, tested, and advocated Analytic Hierarchical Process approaches, but the underlying difficulty of the result has always been the interference of fuzzy or ambiguous components [10]. It’s worth noting that the Standard Hierarchy approach isn’t completely successful in decision-making situations with complex challenges, necessitating certain adjustments to make it more effective. The use of a mixture of fuzzy approaches is one efficient way to improve the efficiency of AHP procedures. This has been shown to be effective in tackling increasingly difficult decision- making circumstances [16]. Geographical Information Systems (GIS) application [17], eco-environmental vulnerability assessment [18], water management plans assessment [19], and risk evaluation of information technology projects [20] are just a few of the domains where fuzzy AHP has been used.
In the field of commerce, [21] employed the fuzzy AHP to identify and assess the success elements in e-commerce. It is obvious from the fuzzy AHP applications that it analyzes both thematic and subjective aspects while making judgments, which was a fundamental flaw in the regular AHP. The combination of fuzzy AHP with dynamic programming in identifying the most optimum forest management choices in order to improve economic, ecological, and social advantages is one of the most well-known studies. It was obvious from the findings that fuzzy AHP is best suited for decision-making situations in which the components or criterion are distinct [22]. Ayyildiz and Taskin Gumus, 2021 contend that the spread, diffusion, and conversion of chemicals in hazardous products endanger the environment and societal life. These substances are deadly. Various measures should be used while moving dangerous items. Thus, identifying and minimizing hazards in hazardous material transportation is critical. Weighing major risk elements for hazardous material transportation operations. They identified significant risk indicators for hazardous material transportation and gathered expert data. Using a twolevel hierarchical framework, assess risk factors the experts’ major and sub-risk factor ratings are then aggregated using modified Delphi. The Pythagorean fuzzy analytic hierarchy process approach is used to determine risk factor weights. The suggested decision-making approach was subjected to a sensitivity analysis [23].
Artificial intelligence systems for comprehending human thought processes and applying them to virtual settings have gained popularity in recent years. Fuzzy logic, which is also recognized as an artificial intelligence technology that allows for modeling human behaviors and mathematical expression of even ambiguous notions, has become one of the most popular ways for solving choice issues. In education, there are several decision- making scenarios. It is very difficult and takes expertise to make fair decisions and analyze students’ achievements without making any errors throughout the assessment and evaluation process [24]. Study goal was to evaluate students’ performance using the Fuzzy Analytic Hierarchy Process (FAHP), a multi-criteria decision-making technique based on the fuzzy logic approach. The suggested system’s foundation in fuzzy set theory ensures that it may profit in modeling these ambiguities in human brain processes, as well as achieve fairer, more sensitive, and objective outcomes. FAHP approaches, which are utilized mostly in making significant business choices and designing smart cars in engineering, have raised questions about whether or not they can be employed in teaching. Their research demonstrated that the FAHP approach may be utilized to evaluate student projects in the classroom.
Reig-mullor, et al., 2020 offer an Extended FAHP model (E-FAHP) in which pairwise fuzzy comparison matrices are represented by (m,n)-trapezoidal numbers with nonlinear membership functions. It has been proved that the suggested E-FAHP structure may be used to decrease a large number of FAHP techniques. A case study was used to compare E-FAHP to Mikhailov’s model, demonstrating that E-FAHP encompasses both linear and nonlinear fuzzy numbers [25].
Mahad, et al., 2019 investigates the use of the Fuzzy Analytic Hierarchy Process (FAHP) to tackle Multi-Criteria Decision- Making (MCDM) issues. According to them, MCDM is a procedure in which a decision maker or a group of decision makers analyze and pick the best options based on the decision maker’s criteria’s. The FAHP approach is implemented using a real-life empirical case of supplier selection. The study’s goals are to-
• Apply the FAHP technique to MCDM issues using various language scales.
• Assess the relative weights of each option in relation to the criteria derived using various linguistic scales.
In their work, they employ three different scales labeled S1, S2, and S3. Their research took into account four criteria- delivery, pricing, service, and payment conditions, as well as three alternatives: Supplier A, Supplier B, and Supplier C. The first goal has been met since FAHP can be utilized to tackle MCDM difficulties. Meanwhile, the comparison for the second goal was done using the Coefficient of Variations (CV). Measure S2 was found to be the best appropriate linguistic scale for the case study [26].
Because of the availability of ambiguous or imprecise criteria that impact the decision, locating underground dams among eligible areas may be a very difficult challenge. Because the actual world is full of uncertainties, imprecise terminology, and unclear terms, decision-making in the area of underground dam building must use more practical and viable language. The creation of the fuzzy set theory was prompted by the vagueness, ambiguities, and uncertainties, particularly in cases when there is a lack of wholesome information from experts. This validation makes it a great time to learn more about fuzzy AHP and put it into practice using software.
Study area
The Sunyani West District is predominantly made-up of farming communities that specialize in the growing of staple crops like maize. Upon deliberation with the Sunyani West District Agric Officer, a list of 8 farming communities were initially selected and in order to further refine the selection criteria of the selected lands some criteria were selected. These eight communities were passed through a local method of selection which considers host factors and factor values. Figure 2 is a map of Sunyani West District from which a host of farming communities were selected.
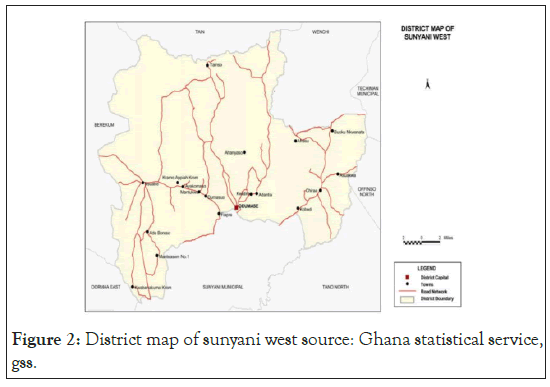
Figure 2: District map of sunyani west source: Ghana statistical service, gss.
Fuzzy analytic hierarchy process
The analytic hierarchy process is a tried-and-true decision- making procedure that works well with multi-criteria decision scenarios [7]. AHP has been shown to be useful in a variety of MCDM applications. In most cases, however, decision makers could only make a judgment based on subjective and imprecise estimations rather than a clear, accurate, and exact response [27]. As a result, it is vital to quantify such responses. The notion of fuzzy comes in handy since it contains structures and approaches that address the setbacks stated in order to comprehensively deal with the vagueness, uncertainties, and ambiguities that define the output of standard AHP methodology.
There has been a lot of interest in employing Fuzzy AHP in various fields because of the fuzzy set theory’s involvement, such as risk and disaster management [28], work safety evaluation [29], and green initiatives in the fashion supply chain [30].
The following methods were used in this study, which were inspired by fuzzy logic and the analytic hierarchy process-
Preliminary evaluation based on ranking initial factors from the evaluation criteria-
A list of alternatives, in this case a set of lands, are considered against some initial factors spelled out by the District Agriculture Officer. Data with respect to these factors are gathered and ranked according to each factor. The data collected for each alternative with respect to the initial factors are summed and four highest alternatives are selected. The ranking algorithm is selected because the data gathered will mostly have un-uniform and distinct scales.
Gathering experts’ judgments based on fuzzy scale and establish fuzzy pairwise comparison matrices-
Experts in hydrogeology and agriculture from the Sunyani West District were contacted, and a set of criteria has been verified. According to AHP, a three- level hierarchical structure must be completed and designed.
Collecting experts’ judgment and generate predicted values-
Interviews were held with experts and research enthusiasts in the topic of study. They were given questionnaires to fill out in order to determine the primary aspects impacting the study topic. The collecting of expert evaluations based on fuzzy scales was inspired by the sample questionnaire [31 and 32]. The notion of Triangular Fuzzy Numbers (TFN) was also employed, which was created to help decision makers make simpler judgments. Values were created and forecasted for each area under examination based on expert assessment, which would eventually help us evaluate the methodology’s efficiency level. The membership functions of the TFN that was implemented and is shown in the equation.
A=(l, m, u), where l ≤ m ≤ u
Where,
L=Minimum possibility factor
M=Most likely possibility
U=Maximum possible value of a fuzzy number

Basic mathematical operations are performed on the l, m, u variables and this shown in equation 2-
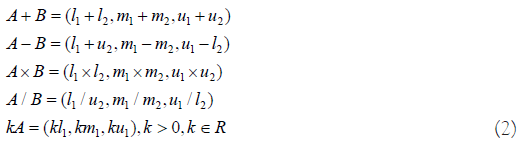
Pairwise comparisons of related matrixes shall further be used. This is a standard requisite of AHP. This is displayed in equation 3.
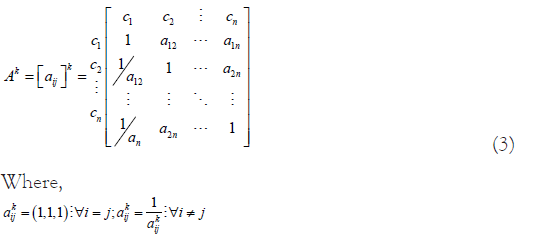
The experts’ judgments are then aggregated using methods [33]. As shown in equations [4-7] where l, m, and u represent the least possible, most probable, and maximum possible values of a fuzzy number, respectively. The following is the definition of TFN KA-
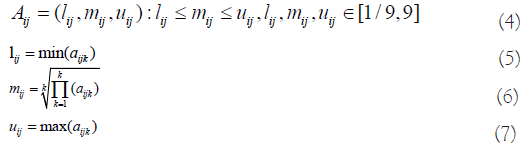
Where aijk show relative important of criteria ci and cj given by expert k
Table 1 shows the linguistic scale and underlying Triangular Fuzzy Number (TFN) based on [27 and 28].
| Fuzzy number | Linguistic scales | Scale of fuzzy number |
|---|---|---|
| 1 | Equally important | (1,1,1) |
| 3 | Weakly important | (2,3,4) |
| 5 | Fairly important | (4,5,6) |
| 7 | Strongly important | (6,7,8) |
| 9 | Absolutely important | (9,9,9) |
| 2,4,6,8 | Intermediate values (x̅) | (x−1, x, x+1) |
| 1/x | Between two adjacent judgments | 1/x+1,1/x, 1/(x-1) |
Table 1: The linguistic scale and underlying triangular fuzzy numbers.
De-fuzzifying the fuzzy pair-wise comparison matrices-
At this stage, the fuzzy numbers are de-fuzzified. This step is done by using the [34] methodology where the fuzzy matrix is transformed into a crisp matrix A
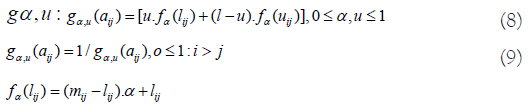
Where is the left – hand value of α - cut and aij and
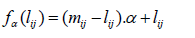
Where is the right- hand value α - cut for aij
The term α index refers to a measure of uncertainty. In a nutshell, α index denotes whether a condition is constant or changeable. The lower the degree of uncertainty, the higher is the α index value. The μ index measures a decision maker’s degree of pessimism while making judgment matrix AK. The lower the μ index value, the lower the degree of optimism (the decision maker is pessimistic). The de-fuzzified pair-wise comparison matrix is expressed by Equation 10
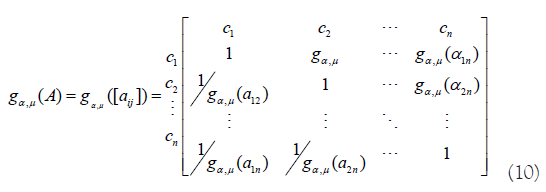
Determining Consistency Rate (C.R.)-
The Consistency Rate (CR) is crucial in determining if the estimated findings are consistent. The eigenvalue (λma) of the single pair-wise comparison matrix, gα,(A), should be obtained first when calculating the Consistency Rate (CR) maximum is derived using equation (11).

After calculating, values of Consistency Index (CI) and CR can be generated from equations (12-13)

Is C.R. <0.1?
The Consistency ratio becomes an acceptable scope if and only if C.R. <0.1. If the C.R does not meet these criteria, matrix modifications become increasingly necessary and hence a new matrix must be generated.
Making the optimal choice by calculating the weights of pair-wise comparison matrices, priority weights for each option, and computing the weights of pair- wise comparison matrices
The W represents weight of pair-wise comparison matrix, g (A). Whereas, the W is eigenvector of matrix, g (A) and can be defined as equation (14).
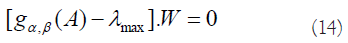
The final weight of the alternatives is obtained after computing the weights for all pair-wise comparison matrices of the proposed hierarchical structure, and then the optimal selection is taken. The weights may be sorted in decreasing order, with the best option being chosen in the end.
As previously stated, the methodology influenced the research’s motivations and aims.
Preliminary evaluation based on ranking initial factors
In order to effectively select the suitable candidate locations from the list of an initial list of 7 communities, a number of factors were selected to guide the screening process of selecting the final four out of the list. The list of locations that qualifies is then given a pass to be evaluated by the fuzzy AHP system. The factors that were considered for this evaluation are-
• Farm Size
• Annual yield of staple crops
• Number of farmers
• Nearness of Site to farms or usage site
Table 2 summarizes the results obtained from the initial evaluation and the rank of the candidate lands with respect to the factors considered. The candidates in terms of highest total selected to the Fuzzy AHP system were-
| Candidate lands | Candidate lands | Factor 2: Annual crop yield (Bags per acre) | Factor 3: Number of farmers | Factor 4: Number of farms | Total |
|---|---|---|---|---|---|
| Kantro | 6 | 4 | 6 | 6 | 22 |
| Ayakomaso | 4 | 3 | 4 | 1 | 12 |
| Mentukwa 2 | 2 | 2 | 2 | 3 | 9 |
| Kobedi | 4 | 7 | 4 | 5 | 20 |
| Bofourkrom | 7 | 6 | 7 | 7 | 27 |
| Tima Nkwanta | 2 | 6 | 1 | 2 | 11 |
| Tanom | 5 | 1 | 5 | 5 | 16 |
Table 2: Rank of candidate lands with respect to selected factors.
• Bofourkrom (A1)
• Kantro (A2)
• Tanom (A3)
• Kobedi (A4)
Criteria and alternatives and established hierarchical structure
According to the technique, thorough study and assessment are performed with regard to the systems principal aim in order to develop a hierarchical structure. Stakeholders in the research area, such as the local agricultural officer and resource people from the department of community water, were consulted extensively. A list of criteria for the fuzzy AHP process was created based on their interactions. The four main factors (Criteria) that were selected are given below in no particular order-
• Distance to Utilization site (C1)
• Wall material (C2)
• General aquifer criteria (C3)
• Slope (C4)
According to the experts, each criteria must have ideal values and requirements that must be satisfied. For C1, the shorter the distance to the utilization location, the cheaper the cost, and hence the better the option. The ideal situation for the wall material to achieve the aim is that the stronger the wall material is, the more likely it is to achieve the goal. To get the best value, the overall aquifer must also be favorable and highly rich. A extremely low slope also means a lengthy distance when the liquid is transported from depth to bed. The ideal slope should be approximately 12% (Nilsson, 1988).The hierarchical structure is structured into three levels and they are namely-
• Level one (goal level)
• Level two (criteria level)
• Level three (alternative level)
The hierarchical structure that represents this research case is illustrated in Figure 3. The hierarchical structure further gives an impression on the pairwise comparison of the criteria and alternative levels. This implies that each factor is mapped against the alternative so as to arrive at the optimal alternative.
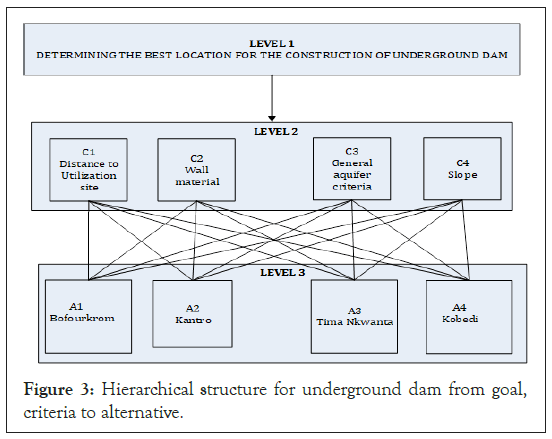
Figure 3: Hierarchical structure for underground dam from goal, criteria to alternative.
Experts’ judgment based on fuzzy scale and establishes fuzzy pair-wise comparison matrices
The concept of underground dams is yet to gain grounds in the Ghanaian jurisdiction and so there a few expects available. However, borehole engineers or groundwater engineers in the local vicinity were engaged to give us their expertise on this subject matter since it all basically entailed groundwater.
Using a structured questionnaire that incorporates the triangular fuzzy representation of data, we were able to arrive at values to undertake the fuzzy comparisons. Table 3 is a structured questionnaire sample containing the assertions made by the experts.
| Criterion | Comparison | ||||
|---|---|---|---|---|---|
| A.Imp (9,9,9) | S.Imp (6,7,8) | F.Imp (4,5,6) | W.Imp (2,3,4) | Eq.Imp (1,1,1) | |
| Distance to utilization site | - | - | - | - | √ |
| Distance to utilization site | - | - | √ | - | - |
| Distance to utilization site | - | √ | - | - | - |
| Wall material | - | - | √ | - | - |
| Wall material | - | - | √ | - | - |
| Aquifer | - | √ | - | - | - |
| Wall material | - | - | - | - | √ |
| Aquifer | - | - | √ | - | - |
| Slope | - | √ | - | - | - |
| Aquifer | - | - | √ | - | - |
| Slope | - | - | √ | - | - |
| Slope | - | √ | - | - | - |
Note: Absolutely Important (A.Imp); Strongly Important (S.Imp); Fairly Important (F.Imp); Weakly Important (W.Imp); Equally Important (Eq.Imp)
Table 3: Sample questionnaire of comparison between criteria.
Appendix 1 contains the details of the questionnaire that was distributed and used.
Equally Important–(Eq. Imp)
Weakly Important–(W. Imp)
Fairly Important–(F. Imp)
Strongly Important–(S. important)
Absolutely Important–(A. Important)
The resultant aggregated fuzzy comparison of level 2 obtained was obtained in Table 4
| Goal | Distance to utilization site | Wall material | General aquifer criteria | Slope |
|---|---|---|---|---|
| Distance to utilization site | 1,1,1 | 1,1,1 | 4,5,6 | 6,7,8 |
| Wall material | 1,1,1 | 1,1,1 | 4,5,6 | 4,5,6 |
| General aquifer criteria | 0.167,0.2,0.25 | 0.167,0.2,0.25 | 1,1,1 | 6,7,8 |
| Slope | 0.125,0.143,0.167 | 0.167,0.2,0.25 | 0.167,0.2,0.25 | 1,1,1 |
Table 4: Aggregated fuzzy comparison of level 2.
De-fuzzifying the fuzzy pairwise comparison matrix
Applying the de-fuzzifying equations 8 and 9 we obtained the de- fuzzified Table 5 below
| Goal | Distance to utilization site | Wall material | General aquifer criteria | Slope |
|---|---|---|---|---|
| Distance to utilization site | 1 | 1 | 5 | 7 |
| Wall material | 1 | 1 | 5 | 5 |
| General aquifer criteria | 0.205 | 0.205 | 1 | 7 |
| Slope | 0.1445 | 0.205 | 0.1445 | 1 |
Table 5: Aggregated de-fuzzified comparison of level.
The Consistency Rate (CR)
In order to establish a solid conformity of the results, the consistency ratio which is backed by equations 11, 12 and 13 is calculated.
With a maximum eigenvalue of the de-fuzzified matrix of 4.0651, a consistency index of 0.0217 is obtained with a consistency ratio of 0.0241 also obtained. It should be noted that the Saaty random scale guided the choice on n in the calculation.
In order of a set of decision matrix to be consistent it must have a consistency ratio below 0.1. In this case the consistency rate of 0.0241 is far below hence very much consistent.
Computing weights of pairwise-comparison matrices and priority weights for each alternative and making a best decision
It is necessary to do a pairwise comparison of each of the alternatives with regard to each of the criteria in order to get the priority weights of the alternatives as specified by the fuzzy AHP approach. Each of the comparison stages is given a fuzzy questionnaire, similar to the ones used in the previous phases, which is then defuzzified, the consistency ratio computed, and the weights of each created.
The local weights of the criteria after computation are displayed in Table 6
| Criteria | Distance to utilization site | Wall material | General aquifer criteria | Slope |
|---|---|---|---|---|
| Priority Weights | 0.4098 | 0.3848 | 0.1530 | 0.0524 |
Table 6: A table displaying the priority weights of each criterion.
After extensive computation and consideration of each criterion and the alternatives, the final weights of alternatives with respect to the selected criteria is summarized in Table 7.
| Criteria | Weights for Level 2 | Weights of level 3 | |||
|---|---|---|---|---|---|
| Bofourkrom | Kantro | Tanom | Kobedi | ||
| Distance to utilization site | 0.40980301 | 0.2464779 | 0.5686827 | 0.1162252 | 0.068614279 |
| Wall material | 0.38480301 | 0.288978 | 0.530512 | 0.110436 | 0.070074 |
| General aquifer criteria | 0.1530113 | 0.2353 | 0.6016 | 0.0739 | 0.0892 |
| Slope | 0.05238268 | 0.2353 | 0.6016 | 0.0739 | 0.0892 |
| Final weight | 0.260536 | 0.560756 | 0.105304 | 0.073404 | |
Table 7: A table displaying final weights of alternatives with respect to all alternatives.
The final weights as displayed Table 8 are ranked so as to firmly ascertain the best alternative. Table 8 displays the final results and the selected alternative.
| Alternatives | Final weight | Rank |
|---|---|---|
| Bofourkrom | 0.260536 | 3 |
| Kantro | 0.560756 | 4 |
| Tanom | 0.105304 | 2 |
| Kobedi | 0.073404 | 1 |
Table 8: A table displaying the ranked final weights.
From, it is very evident that kantro has the highest rank and therefore the highest weight. This implies that Kantro which is alternative, is the best location to site an underground dam in the Sunyani West District.
The fuzzy AHP approach used here is an exhaustive technique that provides a thorough comparison of criteria and alternatives, as well as consistency checks, to ensure that the best and most suitable selections are reached. The following statements were made after defuzzification and creating priority weights-
Alternative 2 (Kantro) had the greatest comparable weights per factor, with values of 0.5686, 0.5305, 0.6016, 0.6016 for C1, C2, C3, and C4 correspondingly. This means Kantro has the best criterion circumstances for achieving the research purpose.
The final calculated weights also indicated that Alternative 2 had the greatest final weight. This means that, in the hazy atmosphere, it is the most appropriate site according to specialists’ view.
To summarize, we were able to conclude that Kantro, which doubles as option 2, fulfilled the ideal proportions that described the best place to build underground dams while using fuzzy AHP to select the best location for the construction of an underground dam.
It should however be noted that the initial judgement made by team of experts in the regional offices of Community water and sewage were corroborated by the outcome of this research. This increasingly affirms the consistency of this selection decision.
1. Fuzzy AHP methodology uses rigorous and lengthy computations techniques and so a multiplatform architecture would be favorable to fully implement this methodology. Ideally a merger of MATLAB and Visual Basic. Net if possible.
2. In order to take proper decisions, strict attention needs to be paid during the implementation stages. The feedback channels must be clear and must give the expert or the decision maker the luxury to enter and manipulate the values with ease.
3. The interaction with the experts revealed the unavailability of some data that could help refine decision that needed to be made. Therefore, data such as general aquifer measurements and the average slope measurement of the various communities should be collected and be readily available to help decisionmakers make such decisions.
1. Fuzzy methods in multi-criteria situations in all facets of decision making, great attention should be paid to decision making. As a result, this technique might be used to other areas of the economy, such as manufacturing and commercial decision- making, to improve decision-making efficiency.
2. Future efforts should concentrate on creating a multipurpose architectural framework that will assist software developers in completely implementing this technique with the user at the centre.
Citation: Damfeh EA, Adakoya AF, Wayor BA (2022) Determining the Best Site Location for Underground Dams Using Fuzzy Analytic Hierarchy Process: A Case in the Sunyani West District. Int J Adv Technol. 13:201.
Received: 28-Jul-2022, Manuscript No. IJAOT-22-17693; Editor assigned: 02-Aug-2022, Pre QC No. IJAOT-22-17693(PQ); Reviewed: 16-Aug-2022, QC No. IJAOT-22-17693; Revised: 23-Aug-2022, Manuscript No. IJAOT-22-17693(R); Published: 30-Aug-2022 , DOI: 10.35248/0976-4860.22.13.201
Copyright: © 2022 Damfeh EA, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.