Journal of Ergonomics1234
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2014) Volume 4, Issue 1
Air conditioning in office spaces is conventionally based on supply of air from the ceiling. Often occupants’ comfort (thermal comfort and inhaled air quality) depends on the interaction of the supplied downward ventilation flow with the thermal plume generated by human body. This interaction is essential for the heat transfer from the human body and thus for its cooling. Convective cooling of the body at warm environment improves peoples’ thermal comfort and may cause thermal discomfort due to draught at comfortable or cooler environment.
Draft is defined as local cooling of the body due to air movement. Studies that consider the issues of draft include those by Houghten et al. [1], Fanger et al. [2,3], McIntyre [4], Mayer [5], Berglund and Fobelets [6], Melikov [7] and Lee et al. [8]. The studies by Houghten et al. [1], Fanger et al. [2,3], McIntyre [4], Berglund and Fobelets [6], Melikov [7] and Lee et al. [8] target forced convection by confronting the airflow from the frontal coronal plane of the body, and do not target downdraft from the upper horizontal plane of the body. On the other hand, Mayer [5] considers the head as the subject but does not consider the influence of other parts of the body.
When taking the air conditioners from the ceiling into consideration for offices, it is essential to have a grasp on the heat balance of the human body when planning, designing or evaluating the thermal environment. The usual angle factor of the human body and radiative heat transfer area is applicable for thermal radiation. In office spaces, the conductive heat transfer area is small. Moreover, the difference between the floor surface temperature and the skin temperature of the body is little. Therefore, It is possible to neglect the heat conduction [9,10]. However, the direction of airflow from the ceiling is different from previous studies. The previous ones are the direction of the confronting airflow from the body’s frontal coronal plane. Therefore, it is indispensable to determine whether the conventional research findings are applicable.
Previous researches on convective heat transfer from human body have focused on experimental rather than theoretical approach. In some studies simple heat emitting devices or assemblies has been used to model the convective heat transfer coefficient of the human body, other studies have used real subjects or thermal mannequins to investigate the heat balance of the human body. The mass and heat transport properties of naphthalene have been used as well. Most of these experimental studies on forced convections use wind tunnels or artificial climate chambers, and focus on the confronted airflow from the frontal coronal plane of the body. Under some conditions natural convection of an updraft from the lower horizontal plane of the body exists, but its characteristics differ from forced convection.
Research focused on the impact of direction of airflow on the heat transfer from human body has been reported [11-15]. Colin and Houdas [11] examined the convective heat transfer coefficient of a human body to airflow from the foot direction of the body to the horizontal plane, and the lateral direction of the body to the sagittal plane, for a body in a dorsal position. de Dear et al. [12] considered the convective heat transfer coefficient of human body in standing and seated posture to airflow from 8 horizontal directions, focusing on the frontal coronal plane of the body. Kurazumi et al. [15] determined the convective heat transfer coefficient of the human body to airflow from the front and back of the coronal plane of the body in a sitting with legs out position, and seated position. Mayer and Schwab [13,14] focused on the head area of the body, and examined the convective heat transfer coefficient of the head to the airflow from above, bellow, front and back. However, the convective heat transfer coefficient of the whole body has not been clarified. de Dear et al. [12] and Kurazumi et al. [15] show that the convective heat transfer coefficient of the human body is significantly different depending on the direction of the airflow.
In the case of air conditioning facilities in the ceiling surface of an office space, the direction of airflow is in downward, vertical to the main axis of the human body in a standing or seated position. However, previous research does not cover the convective heat transfer coefficient of the whole body with respect to the orientation of airflow at all. The purpose of this study was to examine the convective heat transfer by forced convection from seated human body exposed to airflow from above.
In previous studies, the total amount of heat transfer was obtained by using physiological measurements and a heat flow meter. The convective heat transfer was determined by subtracting the radiant heat transfer from the total heat transfer. The angle factor value of the human body is essential to calculate the radiation heat transfer. However, the angle factor value between the measurement unit corresponding to the body section and enclosure has not been determined. Moreover, the appropriateness of the estimated value is inaccurate.
The radiative heat transfer coefficient of the whole body can be calculated in the process of determining the convective heat transfer coefficient or heat balance of the human body, but this specific value is rarely mentioned. Stolwijk, de Dear et al., Ichihara et al., Ishii and Kurazumi et al. have calculated the specific value [12,15-21]. Values provided by Stolwijk, de Dear et al., Ichihara et al. and Kurazumi et al. are for a human body model, and values by Ishii and Kurazumi et al. are for a human body [12,15-18,20,21]. Studies by Stolwijk, de Dear et al., Ichihara et al. and Ishii do not directly measure the amount of radiant heat transfer, but determine the angle factor of the space between the surface and each part, and conduct calculations through the Stefan- Boltzmann law [12,16-18]. On the other hand, the studies carried out by Kurazumi et al. are on directly measured values [15,19-21]. These studies produce results that strongly illustrate the influence of radiative heat transfer area and body surface distribution.
In this paper, the total sensible heat transfer coefficient is obtained through experiments in a thermal environment in which the air temperature and each surrounding wall temperature are equal. The convective heat transfer coefficient, hc can be calculated by using the total amount of sensible heat transfer Q from the body.
Q = C + R (1)
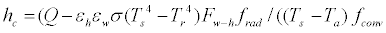 (2)
(2)
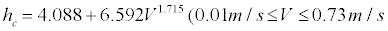 (3)
(3)
Here,
Q: Total sensible heat transfer [W/m2]
C: Convective heat transfer [W/m2]
hc: Convective heat transfer coefficient [W/(m2•K)]
Ts: Surface temperature of the thermal mannequin [K]
Ta: Surrounding air temperature [K]
Tr: Mean radiant temperature of thermal mannequin [K]
εh: Emissivity of thermal mannequin surface [ND]
εw: Emissivity of the interior surface configuration [ND]
σ: Stefan-Boltzmann constant [W/(m2•K4)]
F w-h: Angle factor between thermal mannequin and room configuration [ND] fconv: Convective heat transfer area ratio of thermal mannequin [ND]
frad: Radiative heat transfer area ratio of thermal mannequin [ND].
The experiment was carried out in an experimental test room (4.71 m×5.33 m×2.60 m) located in a large room (11.84 m×9.73 m×10.13 m). The test room was isolated and placed 0.75 m above the floor. The air temperature in the climatic room and experimental test room was kept the same, i.e. mean radiant temperature was the same as the air temperature and radiant temperature asymmetry in horizontal and vertical direction was the same. Air was supplied isothermally downward from the ceiling. The supplied airflow was with low initial turbulence intensity. The size of the air supply device, leveled with the ceiling, was 1.08 m×1.00 m
Human body was resembled by a thermal mannequin with a body surface area of 1.4794 m2. The body of the thermal mannequin was divided into 23 segments: top of head and face (left and right), back of head and neck, chest (left and right), back, abdomen, buttocks, upper arm (left and right), forearm (left and right), hands (left and right), anterior thigh (left and right), posterior thigh (left and right), lower leg (left and right), and feet (left and right), making it possible to control the calorific value and surface temperature of each region. Table 1 shows the surface area ratio of each region of the thermal mannequin. The emissivity of the surface of the thermal mannequin is 0.95.
| Regin | Area ratio [-] |
|---|---|
| Parietal region | 0.034 |
| Left face | 0.018 |
| Right face | 0.017 |
| Back of neck | 0.017 |
| Left upper arm | 0.049 |
| Right upper arm | 0.053 |
| Left forearm | 0.034 |
| Right forearm | 0.034 |
| Left hand | 0.026 |
| Right hand | 0.025 |
| Left chest | 0.047 |
| Right chest | 0.047 |
| Back | 0.088 |
| Abdomen | 0.074 |
| Pelvis | 0.037 |
| Left front thigh | 0.054 |
| Right front thigh | 0.056 |
| Left back thigh | 0.054 |
| Right back Thigh | 0.056 |
| Left lower leg | 0.061 |
| Right lower leg | 0.061 |
| Left foot | 0.029 |
| Right foot | 0.029 |
Table 1: Surface area ratios of segments of thermal mannequin.
The mannequin measurements were taken in a seated position. The thermal mannequin was seated in a support base made with support rods that only touch the mannequin in 3 locations, and the experiment was carried out in conditions where the heat transfer amount between the thermal mannequin and the environment could be ignored. Therefore, all body segments were exposed to the airflow. The thermal mannequin was set up so that the soles of the feet were 0.10 m above the floor. The thermal mannequin and thermal environment were kept in a steady state.
Measurements were performed at two constant levels of air temperature: 26°C (assuming cooling) and 20°C (assuming heating period). The air velocity, determined from preliminary measurements, was set at six levels: still air, 0.2, 0.3, 0.4, 0.5, 0.7 m/s, where is near the top of head at 1.5 m above the floor. Relative humidity was the same for all conditions.
The air temperature and humidity, vertical air temperature distribution, air velocity, and surface temperature of each side of the room configuration were measured for the thermal environmental conditions. A thermistor thermometer was used to measure the air temperature and humidity at 0.93m vertically above the floor at the chestlevel of the mannequin, and the vertical air temperature distribution and surface temperature of each side of the room configuration was measured with a thermistor thermometer at 10 seconds intervals. The vertical air temperature distribution was measured at the soles (0.12 m), lower leg (0.53 m), chest (0.93 m), top of head (1.55 m), and at 2.00, 2.15 and 2.29 m above the floor. The downdraft air velocity sensor itself is a disturbance factor for the distribution of air velocity in the intervening areas of the body. Therefore, prior to the start of the experiments, the air velocity 1.50 m above the floor (corresponding to the top of the head level) was measured using an omni-directional anemometer (measurement accuracy ± 0.03 m/s). The initial velocity field at the air supply device was identified by measurements at 64 points positioned at 0.15 m intervals. Table 2 shows the air velocity and the measured results. During the experiment, the air velocity was controlled by monitoring the amount of air supplied to the room.
| Air flow rate | 0.00 m3/s | 0.17 m3/s | 0.27 m3/s | 0.34 m3/s | 0.46 m3/s | 0.58 m3/s |
| Ta = 20°C | 0.012 ± 0.018 0.193 ± 0.063 0.351 ± 0.065 0.438 ± 0.078 0.586 ± 0.096 0.734 ± 0.124 | |||||
| Ta = 26°C | 0.005 ± 0.004 | 0.170 ± 0.040 | 0.311 ± 0.069 | 0.397 ± 0.083 | 0.544 ± 0.124 | 0.709 ± 0.141 |
Table 2: Measured values of air velocity.
The surface temperature and heat supply to the 23 segments of the thermal mannequin was measured in 10 seconds intervals.
Once thermal equilibrium was established between the thermal mannequin and the surrounding environment, the measurements began. Each region of the thermal mannequin’s electric energy was controlled to maintain each region’s surface temperature at a constant level of 34°C.
After confirming that the set thermal environment conditions and the heat loss from the thermal mannequin were in a steady state, the amount of heat supplied to the thermal mannequin and the surface temperature of the thermal mannequin were recorded. The thermal environment conditions 5 minutes before the end of the experiment and the surface temperature and amount of heat supplied to the thermal mannequin were used for the analysis.
The measured results of the thermal environment are shown in Table 3. The air temperature in setting conditions was kept in the range of ± 0.2°C from the set value. The difference between the mean radiant temperature and the air temperature was about 0.1°C. The calculation of the mean radiant temperature was performed using Fanger et al.’s angle factor value of the human body [22]. The vertical air temperature distribution measured at the vicinity of the thermal mannequin identified almost constant temperature with differences in the range of ± 0.1°C. The supplied airflow rate was stable throughout the experiment. Relative humidity was at around 15%. Therefore the thermal environment during each experiment nearly satisfied all setting conditions. Since the vertical air temperature distribution in the range of the thermal mannequin differed very little (in the range of ± 0.1°C), and the difference between the mean radiant temperature and the air temperature was around 0.1°C, it can be concluded that the thermal environment was nearly homogeneous.
| Air flow rate | 0.00 m3/s | 0.17 m3/s | 0.27 m3/s | 0.34 m3/s | 0.46 m3/s | 0.58 m3/s |
|---|---|---|---|---|---|---|
| Ta = 20°C | 20.19 | 20.60 | 20.47 | 20.42 | 20.30 | 20.29 |
| Ta | ||||||
| Tr | 20.22 | 20.71 | 20.56 | 20.52 | 20.37 | 20.36 |
| ΔTh | 0.13 | 0.04 | 0.05 | 0.05 | 0.04 | 0.04 |
| RH | 19 | 17 | 16 | 16 | 16 | 17 |
| Ta =Ts26°C | 34.00 | 34.00 | 34.00 | 34.00 | 33.94 | 33.80 |
| Ta | 26.03 | 26.19 | 26.30 | 26.30 | 26.28 | 26.27 |
| Tr | 26.01 | 26.18 | 26.30 | 26.31 | 26.29 | 26.29 |
| ΔTh | 0.23 | 0.19 | 0.06 | 0.07 | 0.07 | 0.07 |
| RH | 18 | 14 | 13 | 13 | 14 | 14 |
| Ts | 34.00 | 34.00 | 34.00 | 34.00 | 34.00 | 34.00 |
Table 3: Results of thermal conditions.
The measured results of the thermal mannequin’s surface temperature are shown in Table 3. It was determined to be around 34°C for all conditions. Therefore the thermal mannequin’s environment satisfied the setting conditions.
The convective heat transfer coefficient of the whole body of the thermal mannequin as a function of the air velocity shown in Figure 1. A trend for a larger convective heat transfer coefficient can be seen at a temperature of 20°C when compared to 26°C. Remarkable difference in the heat transfer coefficient at the two temperatures can be seen for velocities up to 0.3 m/s. The buoyancy flow generated by natural convection around mannequin’s body, (due to the temperature difference of the thermal mannequin’s surface temperature and the air temperature as a driving force) can be thought of as being more dominant than the downdraft from the ceiling.
Colin et al. [11] establish the air velocity of confronted airflow from the frontal coronal plane of a body at 0.15 m/s or less as a natural convection region. Rapp [23] defines the confronted airflow from the frontal coronal plane at 0.05-0.2 m/s as a combined convection region, 0.05 m/s or less as a natural convection region, and 0.2 m/s or more as a forced convection region. Mitchell [24] defines the air velocity of confronted airflow from the frontal coronal plane of a body at 0.2 m/s or less as the natural convection region. Mayer and Schwab [13] have clarified the convective heat transfer coefficient for the head in the case of downward flow. At a head surface temperature of 34°C and air temperature of 23°C, downward airflow with velocity of up to 0.3 m/s shows a strong impact on the natural convection and thus on the convective heat transfer coefficient. Lee et al. [8] detected that in forced convection by confronted airflow from the frontal coronal plane of the body at less than 0.2 m/s, the updraft from natural convection makes an impact on the convective heat transfer coefficient. Mochida et al. [25] stated that due to a large variation in measured data from experiments using human subjects, separating the effect of natural convection in the low air velocity range of confronted airflow from the frontal coronal plane of the body is difficult. Judging from the experimental results, the air velocity is inferred 0.3 m/s.
In the present experiment downward flow with velocity of 0.3 m/s and higher became dominant over the upward thermal flow generated over the head of the seated heated mannequin and affected the relationships between the convective heat transfer coefficient and air velocity. Therefore, the interaction between the downward flows with the upward thermal flow is rather complex and different than the interaction of a horizontal flow with an upward thermal flow. In addition, in order to isolate and capture the effect of natural convection from the convective heat transfer coefficient by downdraft from the ceiling is extremely difficult.
The results of this study show that for downward flows with velocity 0.3 m/s and higher the same regression equation can be used regardless of the surrounding air temperature, i.e. 20°C or 26°C. The regression equation for the convective heat transfer coefficient (hc [W/(m2•K)]) for the whole body in forced convection is shown below.
20°C nude seated position downward flow:
hc = 4.088+6.592V1.715 (4)
26°C nude seated position downward flow:
hc = 2.874+7.427V1.345 (5)
Here,
hc: convective heat transfer coefficient [W/(m2•K)] V: air velocity [m/s].
It is difficult to isolate the effect of natural convection from the convective heat transfer coefficient by downdraft from the ceiling, but the regression line slope of the convective heat transfer coefficient at a velocity of 0.2 m/s or less is not strongly affected by air velocity. There are differences in the average values of convective heat transfer coefficient for different temperature conditions. Kurazumi et al. [21] proposed a formula for convective heat transfer coefficient due to natural convection while seated. If the thermal mannequin’s surface temperature and the air temperature differ by 8°C or 14°C, the calculated convective heat transfer coefficient changes by about 20%. The convective heat transfer coefficient at an air velocity of below 0.2m/s at air temperatures of 20°C and 26°C can be expressed respectively at different air temperature conditions at mean values of 4.29W/(m2•K) and 3.04W/(m2•K).
Figure 2 compares the convective heat transfer coefficient of the seated nude body due to downward airflow from the ceiling with the convective heat transfer coefficient of the seated nude body. Since no comparative research has been conducted on the same direction of airflow a strict comparison cannot be done, but the dependent tendency of the convective heat transfer coefficient at an air velocity of 0.2 m/s or more to the air velocity can be regarded similarly in all experiments. Air temperature conditions at 20°C where the temperature difference between the skin temperature and air temperature are nearly equal, show very similar calculated values for forced convection regions over 0.2 m/s as studies conducted by Mochida et al. [25]. In addition, air temperature conditions at 26°C show nearly the same calculated value as those of Mitchell [24].
At air velocities of less than 0.2 m/s, where the effect of natural convection on the convective heat transfer coefficient becomes strong, the convective heat transfer coefficient is strongly affected by the temperature difference between the skin temperature and air temperature. Kurazumi et al. [21] focused on the temperature difference between the skin temperature and air temperature during natural convection, and have proposed a formula for the convective heat transfer coefficient. Comparing the results calculated for different conditions at air temperatures of 20°C and 26°C, either condition shows the convective heat transfer coefficient as a significant result.
The convective heat transfer coefficient of the whole seated body during forced convection by downward flow from the ceiling has been revealed through measurements using a thermal mannequin. At flow velocity over 0.3 m/s, the relationship between the convective heat transfer coefficient and the air velocity does not depend on the surrounding temperature, while at velocity up to 0.2 m/s, the free convection flow plays the major role for the heat exchange. The following empirical formula is suggested for calculation of the convective heat transfer coefficient of the whole body (hc [W/(m2•K)]).
20°C nude seated position downdraft
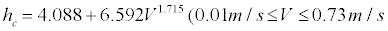
26°C nude seated position downdraft
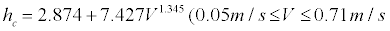
This study was performed at the International Centre for Indoor Environment and Energy, Department of Civil Engineering, Technical University of Denmark.