Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2016) Volume 5, Issue 1
This paper uses the dynamic back propagation (BP) neural network model and the autoregressive moving average (ARMA) model to forecast the RMB exchange rate based on the data from January 1, 2011 to October 10, 2012. The results show that the dynamic BP neural network model works better than the ARMA model in evaluating both the trend and the deviation of RMB exchange rate.
<Keywords: ARMA Model, Dynamic BP Neural Network Model, RMB exchange rate
On July 21, 2005, China reformed the RMB exchange rate by shifting from the U.S. dollar pegged system to the managed floating system. The new system is based on market supply and demand with reference to a basket of currencies. Due to this reform, RMB appreciated sharply by more than 25% and unavoidably, many enterprises were affected. Needless to say, it is highly necessary and important to predict the RMB exchange rate after the reform.
Exchange rate forecast models can be divided into two categories: time series econometric models and nonparametric models. Econometric models of time series include ARMA, ARIMA, ARCH, GARCH model and others. For example, Aguilar and Nydahl [1] adopted GARCH models to analyze exchange rate volatility. Torben [2] improved GARCH model on the limitations of the sample distribution to study the distribution of the daily exchange rate fluctuations of the German Mark and the Japanese Yen against the U.S. dollar. Yu et al., [3] proposed a novel nonlinear ensemble forecasting model integrating generalized linear auto-regression (GLAR) with artificial neural networks (ANN) in order to obtain accurate prediction results and ameliorate forecasting performances. Routa et al., [4] proposed a simple but promising hybrid prediction model by suitably combining an adaptive autoregressive moving average (ARMA) architecture and differential evolution (DE) based training of its feed-forward and feedback parameters. And they used three different exchange rates, Indian Rupees, British Pound and Japanese Yen to simulate and assess its prediction performance. Kuan and Liu [5] used neural networks on five different currencies against the U.S. dollar to forecast exchange rate. Zhang and Hu [6] used the multi-layer neural network to predict the pound and the dollar exchange rate. Thomas et al., [7] used the BP neural network model to predict the U.S. dollar exchange rate. Ince and Trafalis [8] constructed a cointegration equation and artificial neural network model to predict exchange rates. Yu et al., [9] used the RBF neural network model to make predictive analysis. Ye [10] used BP neural network model to predict RMB exchange rates.
As for the predictive effect of these models, however, there is no unanimous agreement. Most of the literature compares the advantages and disadvantages of different models, while some scholars believe that these models have no different predictive effect. For example, Verkooijen [11] reported the results of monthly exchange rate of U.S. dollar against Mark by using of neural network model, and found that the forecasting performance of neural network model sample was very similar to the linear structure model. Sfetsos and Siriopoulos [12], respectively, used a random walk, linear regression, ARIMA and neural network (ANN) to predict GBP/USD daily settlement value and average weekly and monthly exchange rate, the results showed that the projected performance of these models is not so different.
In the foreign exchange market, China has taken a cautious attitude of opening up the RMB exchange rate and thus it is more complex than the mature markets abroad. While ARMA model is a typical model to catch the linearity between different variables, BP neural network model is a typical model to catch the nonlinearity between different variables. Therefore, by providing an example of forecasting RMB exchange rate using both models, this paper serves the purpose to compare the forecast effect of ARMA model and BP neural network model.
Introduction to ARMA model
As an efficient tool in system identification and state prediction for time series data, ARMA model aims at capturing the linear relationships among the variables, with a variety of predefined noise structures taken into account. In this work, ARMA model is introduced to fit the training samples, and its parameters are estimated with least square algorithm. Herein, each state value of the exchange rate in a time-series form can be regarded as a random variable. The dependence among random variables can be expressed as a function that the current value satisfies a linear function of its previous n consecutive values (system model) and its noise model N (t):
y(t) = β1y(t-1) + β2y(t-2) +…+ βny(t-n) + N (t) (1)
Where y (t) denotes the exchange rate value in time t, n is the order of the system model, βi (i= 1,2, ….,n) denotes the ith coefficient. The overall noise model N (t) can be expressed as a linear combination of the error term for m continuous periods:
N (t) = e (t) + α1e (t-1) + α2e (t-2) + αme (t-m) (2)
Where m is the order of the noise model, and αj (j = 1,2,…,m) denotes the jth coefficient of the noise model. Accordingly, the final ARMA model is given by
y(t) = β1y(t-1) + βn y (t-n) + e (t) + α1e (t-1) +… + αme (t-m) (3)
The RMB exchange rate forecast
The data covers the period from January 1, 2011 to October 10, 2012, and the parameters of ARMA model are obtained from Matlab System Identification Toolbox. Huang [13] proposed an effective way, the autocorrelation criterion (AIC), to estimate the optimal lags of the exchange rate time series data. Within certain range of parameters, we select the m,n with the minimal AIC as the simulation parameters of the model, and then identify the ARMA model using the least squares. The estimation results are:
A (q) y (t) = C (q) e (t)
A (q) = 1- 2.839q-1 + 3.094 q-2 – 1.556q-3 + 0.3015 q-4 (4)
C (q) = 1-2.116 q-1 + 1.739q-2 – 0.5719 q-3
Where n = 4, m = 3
The loss function using least square method is 0. 549298, and the final prediction error, FPE, is 0.573557. ‘A (q)’ and ‘C (q) ’are both operators. ‘A (q) y (t)’ describes the linear relationship of the exchange rate in adjacent time sequence. And similarly, ‘C (q) e (t)’ means the linear relationship of the rate error. According to formula (4), we forecast the future exchange rate. Figure 1 is the final renderings of Exchange rate prediction for ARMA model, the first one shows the fitting of the training data renderings; second is rate of the test data prediction; the third piece is the deviation of the predicted value and from the actual value. It is noted that we have conducted DW (Durbin- Watson) test to check the potential autocorrelation in the forecasting errors. The result from the test, DW=1.971194, clearly rejects the null hypothesis that there is autocorrelation in the forecasting errors.
As the length of this sample is 108, we obtain 107 predicted values. And 50 of them have the same fluctuating direction as the actual ones, that is, the accuracy rate is 46.73%. Besides, the RMSE is 0.0665.
Brief description of BP neural network dynamic model
Due to nonlinearity, high parallelism, fault and noise tolerance, and learning and generalization capabilities, artificial neural network has been widely used in control, optimization, classification, prediction, etc. Here, a dynamic model with BP neural network simulation is designed to exchange rates in a time-series form. BP neural network model is the learning process of the error back propagation algorithm which is composed of two processes: the forward transmission and the error. And BP neural network dynamic model considers exchange rates as a time series. And the value of the future exchange rate can be seen as a function of the previous ones. From a mathematical point of view, the nature of the dynamic model is differential equations, while most of financial problems focus on the discrete time sequence, so the dynamic mathematical model can be expressed in the form of differential equations, as equation (5).
x (k) = f [x (k-1), x (k-2)……, x (k-n)] (5)
where x (k), x (k-1), x (k-2)……, x (k-n) is the exchange rate of RMB against U.S. dollar at different time. According to the homogenous ANN model, there is a complex nonlinear relationship between the future exchange rate value and the exchange rate of certain point before. We use the powerful nonlinear approximation ability of BP neural network to learn the neural network, and ultimately find a set of weights so that the neural network model can be a good approximation of historical data and forecast of future data. For simplicity, here we introduce time series operator to make an analysis from the perspective of the signal sampling. For a group of continuous signal, we usually sample the signal and thus make use of these discrete signal for the fast and accurate processing of the computer, here we will see the exchange rate as a series of discrete signals as shown in Figure 2.
And any of them at time t (t = 0,1,…n) can be expressed as:
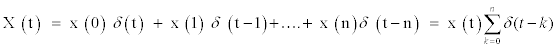 (6)
(6)
Where x (t) means the exchange rate at time t; δ (t) is a unit impulse function:
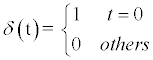 (7)
(7)
After making the Laplace transforms and Z transform on formula (3-2), the final result is:
x (z)= x(0) + x(1) z-1 + x(2) z-2 + ……+ x(n) z-n (8)
Where z-n means the exchange rate value relative to 0 days after the first day, as shown in Figure 2.
Building BP neural network
Same as before, we choose RMB exchange rate from January 1, 2011 to October 10, 2012 as a data source a is the step , l is the number of frames, and then the sample from the data source is collected.
When setting the step, a =1, the optimal minimal AIC implies that l= 4. That is to say, in the data source every four values construct a unit. We select a group of samples from each hop of a data. 4 represent the length of each data set, wherein the first three already known data are the input of the neural network, and the fourth data is output, which is the latest value of exchange rate. If the length of exchange rate series is m (equal to 429), then we get m- l +1 sample groups. We divided the sample into quarter, and the first three quarters are taken as the training sample and the last quarter taken as the out-of-sample to assess the forecasting ability of the network and the ARIMA model.
Once the training and the testing data are obtained, we then use the training data to estimate the optimum weights of the neural network. With respect to a feed forward neural network with p input units, q hidden units (one hidden layer), and r output units, there are totally (p +1)q + (q +1)r weights (threshold included), w to be optimized, whose calculation is based on the following objective function:
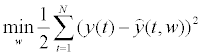
Where y (t) denotes the actual value of exchange rate in time period t, while
Where y (t) denotes the actual value of exchange rate in time period t, while 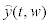 represents the corresponding fitted value, which also can be treated as a function of the weights w. N is the number of the training data. In order to estimate w that achieves the minimum value of the above equation, either the back-propagation algorithm or the intelligent optimization algorithms can be used. Once this training process ends, we can use the testing data to verify the performance of the optimized network.
represents the corresponding fitted value, which also can be treated as a function of the weights w. N is the number of the training data. In order to estimate w that achieves the minimum value of the above equation, either the back-propagation algorithm or the intelligent optimization algorithms can be used. Once this training process ends, we can use the testing data to verify the performance of the optimized network.
RMB exchange rate forecast
Parameter settings: There has not been a uniform standard to determine the number of neurons for the input layer and the hidden layer. Therefore, how long it takes to affect the latest exchange rate is a controversy.
For this reason, we conducted a number of simulations depending on the combination of the number of the input layer neurons and the output layer neuron to find the best combination:
Input layer 3 + hidden layer 7 + output layer 1
We select tansig as the transfer function of the hidden layer neurons, purelin as the conversion function of the output layer neuron, trainlm as learn algorithm, 200 as the number of iterations, 0.2 as the learning rate, and finally, we also allow for deviation of the training data, which is 0.002.
According to the above network simulation, we realize a satisfactory prediction effect. Figure 3a is the simulation interface of the BP neural network tool box, Figure 3b is the convergence map of error function for the training data.
As can be seen from the figure, the neural network learning process went very smoothly, the fitting error of hope can be found only after nine generations of the network and it took less than 1 second. From the figure, the error function of the training data quickly converge to 0.001 or less, so the local optimum of the error function here don’t have to consider the use of genetic algorithm and other optimization methods for solving. It should be noted that, the artificial neural network may exist the over fitting problem. As a result, it is necessary to make a tradeoff between the complexity of the network structure and the number of the training samples. Actually, a small number of the training samples with a complex network structure will lead to over fitting problem due to the positive value of the degree of freedom of the network by Chen et al., [14]. In order to solve this problem, several empirical criterions have been proposed, e.g., adding a regularization term, invoking some prior information, fulfilling early stopping in the network training process, etc. according to Bishop [15]. Note that in our manuscript, the number of the training data (exchange rate) is large and sufficient (321 samples), and the network is 3-7-1, so that a relatively complex network structure will not affect the model precision or its generalization ability. More to the point, the number of the input and hidden units is selected using AIC, ensuring that the neural network which has been trained is reliable.
The prediction of the direction of the fluctuation of the exchange rate: In the exchange rate forecast, the direction of the fluctuation of the exchange rate has become an important decision-making of investors. Therefore, the accuracy of the direction of the predicted fluctuations is an important indicator of the effect of the forecast. For measuring the accuracy of fluctuations direction, we can compare the situation of exchange rate fluctuations in two consecutive time points for judgment, namely:
If (x (k) - x (k-1)) X (x* (k) - x* (k-1)) > 0; it indicates that the direction of fluctuation prediction is accuracy.
If (x (k) - x (k-1)) X (x* (k) - x* (k-1)) < 0; it indicates that the prediction of fluctuation direction fails.
x (k), x (k-1) Represent the K day and k-1 day of the actual value of the exchange rate respectively. x* (k) and x* (k -1) represent the predicted ones accordingly.
Through Mat lab simulation, from 105 set of test sample data, we finally obtained 62 predicted fluctuations of the 104 cases that are consistent with the actual fluctuations. Equivalently speaking, the accuracy rate for fluctuation direction is 59.62%.
Prediction of the RMB exchange rate deviation: Exchange rate deviation between predicted and actual values is another important indicator to evaluate the fitting accuracy of dynamic model of neural network. Even if the accuracy in the direction of exchange rate is great, too large deviation of the predicted values from the actual ones will make this fitting less meaningful. Therefore, only when the degree of accuracy is high and the direction between predicted and actual values is smaller, we can adopt the BP neural network. Figure 4 are the ultimate renderings of BP neural network exchange rate forecasting dynamic model. The first one is the fitting of the training data; the second piece is the test data prediction; the third piece is the deviation curve of predicted values and the actual value of test data.
After training, the network weights matrix is shown in Table 1. And we can get the root mean- square -deviation of test data is 0.0519.
| Weight of Hidden layer | -3.244 | 4.9374 | 0.4885 | 3.4861 | -3.978 | -4.6631 | 3.5186 |
|---|---|---|---|---|---|---|---|
| 1.7091 | -3.7523 | 0.0819 | 1.7985 | 3.0922 | 0.1465 | 2.2846 | |
| 3.5785 | -2.106 | -2.73 | 4.0072 | -0.5315 | -2.4995 | -8.7429 | |
| Threshold value of Hidden layer | 3.8815 | 0.1068 | 1.9912 | -6.2571 | 0.6283 | 0.5271 | -2.2375 |
| Weight of Output layer | -0.0294 | -0.339 | -0.1682 | -0.0054 | -0.405 | -0.0566 | 1.3199 |
| Threshold value of the output layer | 1.7554 | ||||||
Table 1: The list of model weights for BP network dynamic model.
Comparative analysis of BP neural network dynamic model and the ARMA model of the RMB exchange rate forecast: Figure 5 is a combination of the result of exchange rate forecast in Figure 1 and Figure 3b, from comparison, we can see that the predicted effect of the dynamic model of BP neural network is better than that of the ARMA model both in the direction of fluctuation and the predicted error.
As for the forecast on the direction of the RMB exchange rate fluctuation, the accuracy rate is 59.62%, higher than that of ARMA model, which is 46.73%. Furthermore, we continue with Diebold- Mariano test to have S (1) =3.167 with p-value = 0.0015, which reject the null hypothesis that ARIMA model works better than BP model. As for the test data on the deviation of RMB exchange rate, BP neural network dynamic model is 0.0519, which is less than 0.0665 of the ARMA model.
In predicting exchange rate, ARMA model and BP neural network model are ideologically consistent in that both are based on the idea that the future exchange rates are determined by the previous ones. They differ with each other, however, in one fundamental point. The ARMA model roughly considers this recursive relationship as linear even though the accuracy of the model could be improved with the introduction of the error term. Nevertheless, the innate complex nature of the exchange rate implies that a nonlinear relationship is more appropriate, and this is the key reason why BP neural network model is better. Therefore, the prediction of exchange rates made by BP neural network has greater reliability.
In terms of market openness and influential factors, China’s foreign exchange markets is more complex than the mature foreign exchange markets in developed countries , and thus a simple linear regression model is clearly not enough to predict and analyse the RMB rate. In conclusion, we need a nonlinear regression model for dynamic prediction analysis. This paper compares and analyses the linear ARMA model and nonlinear dynamic model of BP neural network. The results show that in terms of the fluctuation direction and prediction deviation for the exchange rate of RMB against U.S. dollar, BP neural network dynamic model indeed surpasses the ARMA model.
This paper is sponsored by National Natural Science Foundation of China (Grant No. 71303078).