Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2013) Volume 2, Issue 1
In this study, we focus on the structural change in production technology and show that the capital-skill complementarity explains the phenomenon of jobless recovery better without any assumption of nominal rigidity. In particular, we show that the job creation for unskilled worker becomes more sluggish as capital-skill complementarity intensifies. The result implies that we did not observe jobless recovery three or four decades ago because the capitalskill complementarity was not strong enough then. Sluggish job creation in recent decades could be due to the facts that skilled labor has become more complementary to capital.
<Keywords: Jobless recovery, Capital-skill complementarity, Real business cycle model
When an economy is in recession, the government and the central bank conduct expansionary economic policies to boost aggregate demand. Those policies have been effective for job creation up to the 1980s, but do not appear to be so after 1990. For instance, the unemployment rate after the trough of June 2009 still remains around nine percent, leading many economists to call this “jobless recovery”1.
People define jobless recovery as the episode of economic recovery which does not reduce unemployment. Figure 1 shows that the US real GDP typically starts growing after the end of a recession. People expect robust job creation as output grows, but this was the case only until the 1980s. Figure 2, which is generated with the Current Employment Statistics (CES) data, shows that the nonfarm payroll employment began growing almost immediately after the end of the recessions in the 1960s, 1970s, and 1980s. Twenty four months into the recovery, employment was about five percent higher than the trough month. However, the recoveries after the trough of 1991, 2001, and 2009 did not keep up with the people’s expectations. Two years into the recovery after the 2001 recession, the economy had yet to reach the employment level of trough. Job creations after the recessions in 1991 and 2009 were very sluggish compared to the average of the 1960s-1980s.
This study focuses on the structural change in production technology. As Berman et al. [1] indicate, there has been (unskilled) labor-saving technological progress. Also international trade has made the US economy an importer of unskilled labor-intensive products (e.g. garments) and an exporter of skilled labor-intensive products (e.g. aircraft). These changes imply that the shape of the aggregate production function should have been affected substantially over time. This paper shows that if we classify labor input by skilled and unskilled labor and impose capital-skill complementarity, then the phenomenon of jobless recovery can be better explained without any assumption of nominal rigidity 2.
The hypotheses of jobless recovery are surveyed well by Aaronson et al. [2]. They list hypotheses such as: Sectoral labor reallocation, just-in-time hiring through the temporary service industry, increase in benefit costs (the health care cost in particular), and the elevated level of political and economic uncertainty. Bernanke [3] stresses the contribution of the expansion in productivity: In the 1990s, firms invested heavily in high-technology equipment, which enabled the firms to meet the growth in final demand for their output without hiring new workers. The National Income and Product Account (NIPA) data support the Bernanke’s hypothesis very well: Firms start investing after trough, while they do not hire more workers. Figure 3 summarizes the movement of private investment on equipment around cyclical trough. This figure indicates that the increase in equipment investment after the trough in 2009 is stronger than the average of the 1960s-1980s. The increase of equipment investment after the 1991 recession is comparable to the case before the 1990s. After the 2001 recession, the growth in equipment investment is weaker than the average of the pre-1990 cases. However, after two years into the recovery, equipment investment became at least higher than the trough level 3. Figures 4 and 5 also indicate that firms are as active in installing new machinery after 1990 as before. In particular, the spending on the information processing equipment and software has been almost consistently increasing without regard to business cycles.
Bernanke’s hypothesis is consistent with the empirical study by Autor et al. [4]. They show that computers substitute for workers who carry out routine tasks and complement workers who carry out nonroutine tasks 4. They predict that industries that are initially intensive in the labor input of routine tasks will make relatively larger investments in equipment as prices decline. Figure 6 describes the changes in employment for different occupational groups. The first three groups, managers, professionals, and technicians, are typically highly-educated and highly-skilled occupations. Employment growth in highly-skilled occupations is robust for the past three decades. The next four columns display employment growth in less-skilled occupations; sales, office and administration, production, craft, repair workers, operators, fabricators, and laborers. The growth rates are relatively sluggish as compared to the first group and have been hit hard by the most recent recession.
There is other evidence that supports this view. Figure 7 describes the trends in weekly real wages by education. Since the 1980s, the real wages for post-college graduates and college graduates have been consistently increasing, while the wages for high school dropouts and high school graduates have been declining or sluggish. The reshaping of the distribution of earnings is documented in Amiti and Stirob [5], Blank [6] and Autor [7]. Krusell et al. [8] explain the dramatic change in the skill premium with a production function featuring capital-skill complementarity.
The ongoing evidence from empirical studies implies that unskilled workers are crowded out by the introduction of highly productive equipment. Therefore, we can easily hypothesize that firms are moving toward an (unskilled) labor-saving and capital-intensive production process as equipment becomes relatively less expensive. Because unskilled workers comprise the majority of the labor force, a sluggish job creation for unskilled workers would result in jobless recovery. If the hypothesis turns out to be a good explanation for jobless recovery, we would need to reconsider the macroeconomic modeling strategy, because the standard Dynamic Stochastic General Equilibrium (DSGE) model does not account for the complementarity between capital and skilled labor and the substitutability between capital and unskilled labor. Therefore, we incorporate the capital-skill complementarity in a general equilibrium framework and examine whether the jobless recovery can be observed from the model. The model is an extension of the standard real business cycle model: The representative household is composed of skilled workers and unskilled workers. The representative firm produces a final good with three inputs: Capital, skilled labor, and unskilled labor, with a Constant Elasticity of Substitution (CES) production technology 5. The intensive and extensive margin of the labor supply is assumed following Bils and Cho [9]. We consider an investment-specific technology shock proposed by Greenwood, et al. [10], as well as a standard neutral technology shock, to account for the accelerated decline in the price of equipment 6. The introduction of the investment-specific shock to the model is important because of Fisher’s [11] finding that the investment-specific shock accounts for the majority of the fluctuations in labor input and output.
With the standard parameter values being imposed, we show that the responses of the demands for skilled and unskilled labor become substantially asymmetric as the capital-skill complementarity intensifies. In particular, the demand for unskilled labor responds little to an investment-specific technology shock while the demand for skilled labor responds robustly. This episode represents jobless recovery because unskilled workers make up the majority of the labor force. We can conjecture that we did not observe jobless recovery three or four decades ago because the capital-skill complementarity was not strong enough. Sluggish job creation in recent decades could be due to the facts that skilled labor has become more complementary to capital.
This paper is organized as follows: Section two presents the feature of the model. The calibration of the benchmark model and the alternative models is discussed in section three. Section four compares the dynamics of the models and discusses the sources of the differences. Concluding remarks follow in section seven.
The model is an extension of a standard real business cycle model whose economy is com- posed of a representative household and a representative firm. Major extensions of the standard model are as follows: First, we consider skilled and unskilled workers to account for the asymmetric effect of a technology shock. Second, we classify labor input with intensive and extensive margins to address the issue of unemployment. As Bachman [12] points out, firms may adjust work hours to a technology shock before adjusting the number of workers. Third, production technology is represented by the CES function which nests the Cobb-Douglas function. Thanks to the flexibility of the CES function, we can examine the dynamics of the model using different levels of capital-skill complementarity. Fourth, we assume the variable capital utilization which gives an additional margin of capital service sup- plied by the household. The variable capital utilization reinforces the asymmetric responses of the demands for skilled and unskilled labor. Fifth, an investment-specific technology shock is considered along with a neutral technology shock, to deal with the technological progress which makes the price of machinery less expensive 7.
Household
Suppose there are two types of workers in the representative household: skilled and unskilled workers. Skilled workers are comprised of ω (0<ω<1) of the household’s labor force and unskilled workers are (1−ω) of it. Let us assume that the two types of workers share the consumption good equally 8. The household provides skilled and unskilled labor services and capital services to the firm. Following Bils and Cho [9], the intensive and the extensive margins of labor input are assumed: The effective hours of labor can be varied by changing the number of workers as well as by the number of hours at work per worker.
The objective of the household is
max Et 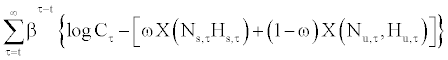 (1)
(1)
where Cτ, Ni,τ, and Hi,τ represent consumption, weeks of work per period, and hours per week for i ∈{s, u}. The subscripts s and u indicate skilled and unskilled worker. The household’s impatience is represented by β which ranges between 0 and 1. The disutility from working is specified by
X (Ni,τ, Hi,τ) =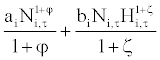 (2)
(2)
The first component represents the disutility of being at work for a fraction Ni of the week in a period and the second one reflects the disutility of total working hours at the workplace. The employment (Ni,τ) and hour (Hi,τ) are normalized, so they take values between 0 and 1. Since the employment is normalized, we can regard it as the employment-to-population rate. The positive parameters ai and bi determine the relative importance of leisure over consumption. The parameters φ and ζ represent the inverse elasticity of the labor supply which takes values larger than −1.
We assume that the equilibrium wage bill is determined as Bils and Cho [9] suggest: The household presents its employer with a wage bill that takes the form of X (Ns,τ, Hs,τ) and X (Nu,τ, Hu,τ) and allows firm to freely choose the size of employment and hours per worker. Because the payment exactly compensates for the worker’s disutility, there is no room for wage rigidity. The equilibrium (real) total wage, TWi,τ takes the following form:
TWi,τ=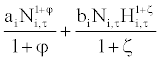 (3)
(3)
for i={s, u}.
The household owns capital stock (K) and provides its service to the representative firm. As assumed in Christiano et al. [13], the service of capital (Q) depends on the unit of capital (K) and the utilization rate (u):
Qτ = uτ Kτ (4)
Because it takes time to assemble a new machine, the household may meet a higher demand for capital service by increasing the utilization rate. Meanwhile, the household has to pay for the cost of setting the utilization rate, γ (uτ) Kτ, which is an increasing, convex function of uτ. We assume that γ (1)=0 and γ′′ (1) /γ′ (1)=σγ. The dynamics depends on σγ but the steady state does not. The economy is subject to an investment-specific technology shock as assumed by Greenwood et al. [10] and Fisher [11]. Assuming the technology shock, the law of motion of the capital stock is given by
Kτ+1 =(1−δ)Kτ+Vτ Iτ (5)
where
log Vτ=ρv log Vτ−1+εv,τ, 0<ρv<1 (6)
It and δ are investment on capital stock and the depreciation rate. The depreciation rate takes a value between 0 and 1. The level of the investment-specific technology shock is denoted by Vt. The larger Vt, the smaller the cost of investment. Considering all the sources of income, the household’s budget constraints is given by
Cτ+Iτ ≤ [Rτ uτ−γ (uτ)] Kτ+ωTWs,τ+(1−ω) TWu,τ (7)
By assumption, the household is ready to provide as much labor service as possible if the payment is right. Therefore the household’s choice variables are {Ct, ut, Kt+1} and the corresponding first order conditions are1
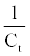 =λt (8)
=λt (8)
Rt= γ′ (ut) (9)
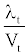 =βEt λt+1
=βEt λt+1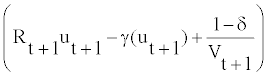 (10)
(10)
Firm
The representative firm produces the final good with the input of skilled labor, unskilled labor, and capital. The inputs are transformed into the output by the CES technology as assumed in Krusell et al. 8. The production technology is subject to a neutral technology shock. The technology is represented by
Yt =At 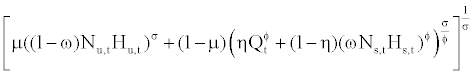 (11)
(11)
where Yt and At represent the output level and the neutral technology factor, respectively. The parameters μ and η govern the income shares, and σ and ϕ do the elasticity of substitution among skilled labor, unskilled labor, and capital. Parameters μ and η ranges in [0,1] while σ and ϕ are real numbers in (−∞, 1). If we impose σ → 0 and ϕ → 0, then equation (11) becomes a standard Cobb-Douglas form, where μ, (1−η)(1−μ), and (1−η)μ indicate the income shares of unskilled labor, skilled labor, and capital, respectively. The elasticity of substitution between capital (or skilled labor) and unskilled labor is 1/(1−σ) and that between capital and skilled labor is 1/(1−ϕ). As shown by Krusell et al. [8], σ>ϕ implies capital-skill complementarity. Neutral technology evolves as follows:
log At=ρa log At−1+εa,t, 0<ρa<1 (12)
The firm would like to maximize its profit given by:
Πt=Yt−Rt Qt – ω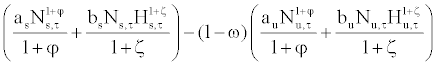 (13)
(13)
subject to equations (11) and (12). The last two terms in equation (13) indicate real wages to be paid to skilled workers and unskilled workers. The first order conditions with respect to Qt, Nu,t, Hu,t, Ns,t, and Hs,t are
Rt=At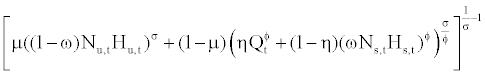
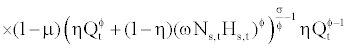 (14)
(14)
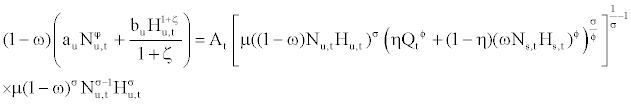 (15)
(15)
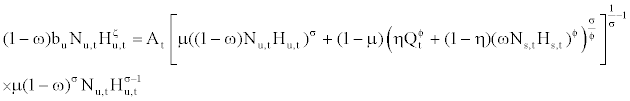 (16)
(16)
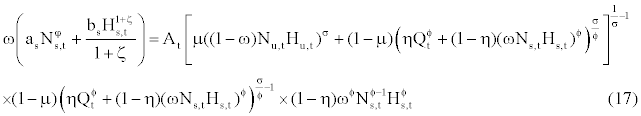
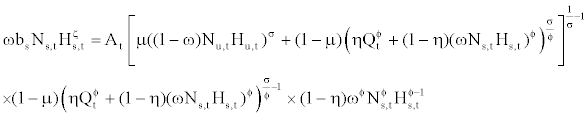 (18)
(18)
The market clearing condition is represented by:
Yt= Ct+ It+ γ (ut) Kt (19)
The solution procedure is very standard: The model is log-linearized around the steady state value and solved by the generalized Schur decomposition method of Klein [14].
Calibration
We use a Cobb-Douglas production function for the benchmark model. Standard values are imposed for parameters, other than the ones for the production function, and remain unchanged throughout the paper. The imposed parameter values for the benchmark model are summarized in Table 1.
| Parameter | Value | Remarks |
|---|---|---|
| β | 0.9900 | Discount rate |
| δ | 0.0250 | Depreciation rate |
| σ | 0.0010 | Parameter for the capital-labor elasticity of substitution |
| ϕ | −0.0010 | Parameter for the capital-skill elasticity of substitution |
| µ | 0.4430 | Distribution of income to unskilled labor |
| η | 0.4750 | Distribution of income to capital and skilled labor |
| ω | 0.2400 | Share of skilled labor |
| φ | 1.5700 | Parameter for the elasticity of employment supply |
| ζ | 2.0000 | Parameter for the elasticity of hour supply |
| σγ | 2.0200 | Parameter for the elasticity of capital utilization |
| ρv | 0.9000 | Persistence of investment-specific shock |
| ρa | 0.9000 | Persistence of neutral shock |
Table 1: Parameter Values for the Benchmark Model.
Assuming two percent of the real interest rate and two percent of the economic growth in the steady state, the discount rate β is set to 0.99 9. We impose 0.025 on the depreciation rate (δ) which means around 10 percent of the annual depreciation rate. Following Lindquist [15] the share of the skilled worker (ω) in the total labor force is set to 0.24. We impose 2.02 on the parameter for the elasticity of capital utilization (σγ) using the estimation result by Altig, et al. [16].
Because the benchmark model utilizes the Cobb-Douglas production technology, the elasticities of substitution between capital and unskilled labor and between capital and skilled labor have to be very close to one. Therefore we impose σ=0.001 and φ=−0.001 10. Since σ>φ, there is some sort of capital-skill complementarity, but it is negligibly small. The parameter values for the elasticity of worker and hour supply are imposed according to the calibration of Bils and Cho [9]: ϕ=1.57 and ζ=2.00 11. The steady state employment- to-population rates for skilled worker (Ns) and unskilled worker (Nu) are set to 0.7705 and 0.5377, which are the average employment-to-population rates of the college graduate and the high school graduate or less educated in the U.S. during 1992-2010. The steady state working hour of unskilled worker (Hu) is set to 0.3333, which implies that unskilled workers spend eight hours per work day at the workplace. Following Welch [17], we assume skilled workers supply 19 percent more working hours than unskilled workers, thus Hs is set to 0.3967. The parameters that determine the income share are calibrated as μ=0.4430 and η=0.4750 to set the steady state relative wage rate of 1.73 for skilled worker. The scale coefficients ai and bi for i ∈ {s, u} in the utility function are obtained by solving for the equilibrium conditions satisfied in the steady-state.
We impose two different sets of {σ, ϕ} on alternative models. The parameters for these alternative models are presented in Table 2. The first set is {0.401, −0.495} which is based on the estimate of Krusell et al. [8]. This implies the elasticity of substitution between capital and unskilled labor of 1.669 and that between capital and skilled labor of 0.669; so capital and unskilled labor are substantially substitutable, while capital and skilled labor are significantly complementary. Since the estimates of {σ, ϕ} by Krusell et al. [8] are based on data between 1962 and 1992, we need to consider the case where capital-skill complementarity has been intensified. Therefore we consider a larger substitutability and complementarity in the second set of {0.7,−2.0} which almost doubles the elasticity between capital and unskilled labor (3.3333) and also reduces the elasticity between capital and skilled labor by about fifty percent (0.3333).
| Model | σ | ESK,U | ϕ | ESK,S |
|---|---|---|---|---|
| Benchmark | 0.0010 | 1.0010 | −0.0010 | 0.9990 |
| Alternative (1) | 0.4010 | 1.6694 | −0.4950 | 0.6689 |
| Alternative (2) | 0.7000 | 3.3333 | −2.0000 | 0.3333 |
Table 2: Parameter Values for Alternative Models.
Impulse response functions
We can analyze the dynamics of the labor market using two different technology shocks: A neutral technology shock and an investment-specific technology shock. A neutral shock directly affects the productivity of each factor and an investment-specific shock affects it indirectly by reducing the relative price of the investment good.
Responses to a neutral technology shock: Figure 8 is the response of the benchmark model to one percentage point increase in the neutral technology level. Since the neutral technology shock has a direct effect on the productivity of every input factor, the demand for skilled and unskilled labor increases in the impact period 12. The increase in the productivity of capital triggers higher investment, so capital stock gradually increases. To meet the increased demand for capital service, the household increases the capital utilization rate since it takes time to accumulate capital. The shock affects skilled and unskilled worker’s productivity symmetrically, thus we can identify the employment of skilled worker (Ns) and that of unskilled worker (Nu) are having identical responses. The work hours of skilled worker (Hs) and unskilled worker (Hu) also respond identically. Since the elasticity of worker supply is larger than that of hour supply (1/φ>1/ζ), the increase in employment is larger than the increase in work hours.
We can identify the change in the dynamics when capital-skill complementarity is imposed. Figure 9 plots the impulse responses of variables when σ=0.401 and ϕ=−0.495. The dotted line represents the response from the benchmark model. The difference is realized as time goes by. Because the productivity of capital and skilled labor increases proportion- ally and the capital-skill complementarity is stronger, employing more capital service and skilled labor has a synergy effect. Hence, the firm has a stronger incentive to input more capital service and skilled labor than the benchmark model. As the input of capital service increases, the demand for unskilled workers and hours declines, so the positive responses of Nu and Hu fall short of the responses from the benchmark model after about ten quarters of the shock. In the meantime, the demand for skilled labor (Ns and Hs) remains stronger than the benchmark response for more than twenty quarters.
When we impose a stronger assumption on the capital-skill complementarity, the difference in the dynamics becomes more apparent. Figure 10 describes the responses to the shock when σ=0.7 and ϕ=−2.0. Again, the demand for unskilled worker jumps up in the impact period but declines to a level less than the benchmark model after about ten quarters. The demand for unskilled hours increases as well, but it becomes weaker than the benchmark response after seven quarters of the shock. Investment and capital accumulation are much stronger than the benchmark level and the demand for skilled workers and their hours are greater than the benchmark case for twenty quarters.
We can also examine the relative demand for each labor service using the response of the relative wage rate. However, the wage rate is not explicitly specified in the model. So we can approximate the wage rate by the sum of the marginal worker cost and the marginal hour cost
Wi,t =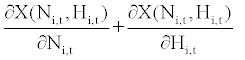 (20)
(20)
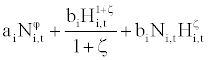
for i ∈ {u, s}. Then the relative wage is represented by
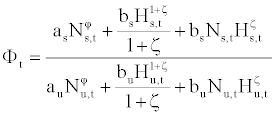 (21)
(21)
If we log-linearize equation (21), then we may examine the impulse response of the relative wage rate to a neutral technology shock. The result is presented in Figure 11. Suppose the impact period is one. When we assume unitary capital-skill complementarity, the relative wage barely responds to the technology shock. On the other hand, the response of the relative wage is more pronounced as the capital-skill complementarity intensifies, which implies that the demand for skilled labor service becomes greater 13.
Responses to an investment-specific technology shock: We need to pay more attention to the investment-specific technology shock because the shock accounts for the majority of the fluctuations in labor input and output as shown by Fisher [11]. Figure 12 displays the dynamics of the benchmark model to a positive investment-specific technology shock. The magnitude of the shock is one percentage point. Since the shock does not enhance the productivity of each input directly, the magnitude of the response is relatively smaller than the case of the neutral technology shock. The shape of the responses is qualitatively consistent with those of Fisher [11]. As the investment good becomes relatively less expensive, the intertemporal substitution of current consumption and leisure for future consumption is amplified. Since current consumption is more expensive relative to future consumption as compared to the neutral shock case, the household consumes less and works more to invest more. Unlike the neutral technology shock, the investment-specific technology shock increases output and labor demand gradually, resulting in a hump-shaped impulse response, because the increase in investment is offset by the decrease in consumption in the impact period. The dynamics are very symmetric as compared to skilled and unskilled labor as noted previously in the case of the neutral shock. Because the elasticity of worker supply is greater than that of hour supply, the response of employment is also greater than that of hour.
Capital-skill complementarity changes the nature of the dynamics. Figure 13 shows that the demands of skilled and unskilled labor clearly respond asymmetrically when the unitary capital-skill complementarity is abandoned. Because the shock reduces the cost of investment, investment increases after the shock. Then the firm employs more capital services which become relatively less expensive. The increased input of capital service increases the productivity of skilled and unskilled labor. A larger capital-skill complementarity implies that the firm will demand more skilled labor as they employ greater capital service. There- fore, the responses of skilled employment (Ns) and skilled hour (Hs) are greater than in the benchmark case. On the contrary, the responses of Nu and Hu become considerably weaker. When we use the alternative model (2), which assumes the strongest capital-skill complementarity, the asymmetric response becomes more pronounced. Figure 14 shows that the demand for unskilled labor responds little to the shock, while that for skilled labor responds more than in the benchmark case. Because unskilled workers make up the majority of the labor force, the overall job creation would not be strong enough; this is a good description of jobless recovery.
The response of the relative wage is consistent with the response of the labor demand. Figure 15 shows that the relative wage does not change when we assume the Cobb-Douglas production function. As the capital-skill complementarity becomes stronger, we can identify that the relative wage gap becomes larger also.
In summary, we show that the job creations for skilled and unskilled workers become substantially asymmetric as the capital-skill complementarity intensifies. In particular, the demand for unskilled labor responds little to an investment-specific technology shock, while the demand for skilled labor responds robustly. This episode represents jobless recovery because unskilled workers make up the majority of the labor force. We can conjecture that three or four decades ago we did not observe jobless recovery because the capital-skill complementarity was not strong enough. Sluggish job creation in recent decades could be due to the fact that skilled labor has become more complementary to capital. Meanwhile, the complementarity is a crucial factor in accounting for the relative wage hike which is observed in the labor market.
In the previous subsection, we identified the asymmetric response of the labor demand to a technology shock. The asymmetry becomes more apparent when we consider an investment- specific technology shock. A positive technology shock, either a neutral or an investment-specific shock, increases the productivity of capital and thus investment. The larger input of capital service enhances the labor productivity. In the model utilizing a Cobb-Douglas production function, this indirect productivity enhancement is symmetric to skilled and unskilled labor. However, it becomes asymmetric when we assume the capital-skill complementarity. As the firm inputs more capital service, which is a complement to skilled labor and a substitute for unskilled labor, the firm needs more skilled labor service. Therefore, unskilled labor is crowded out of the workplace.
To be more specific, let us examine the marginal product of labor. The benchmark model utilizes a Cobb-Douglas production function
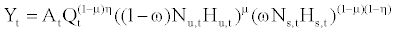 (22)
(22)
Thus, the log-linearized equations for the marginal products of unskilled worker and hour are represented by
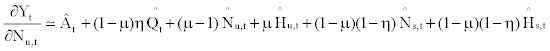 (23)
(23)
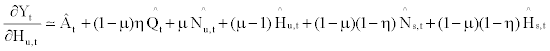 (24)
(24)
where 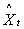 denotes the deviations of a variable Xt from its steady state value X . On the other hand, the equations for the marginal products of skilled worker and hour are represented by
denotes the deviations of a variable Xt from its steady state value X . On the other hand, the equations for the marginal products of skilled worker and hour are represented by
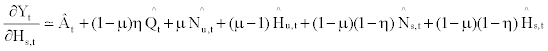 (25)
(25)
and
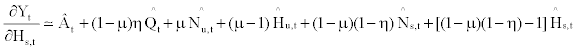 (26)
(26)
These equations imply that the marginal product of skilled and unskilled labor services are equally affected by the change in the capital input (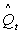 ), with the magnitude of (1−μ)η.
), with the magnitude of (1−μ)η.
When the unitary capital-skill complementarity is discarded, we can represent the marginal products of different labor services as:
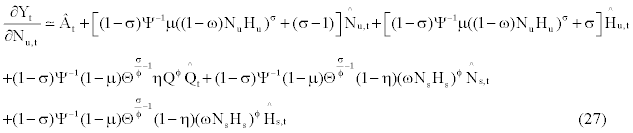
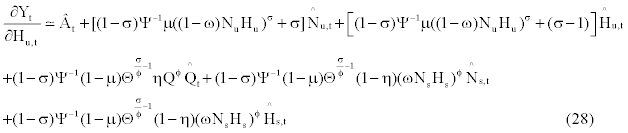
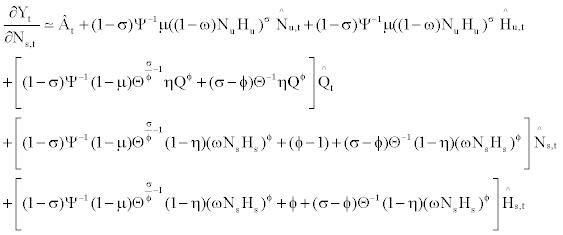 (29)
(29)
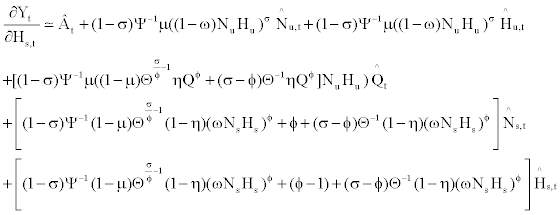 (30)
(30)
where
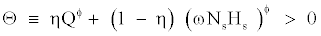 (31)
(31)
and
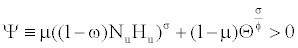 (32)
(32)
If we assume the capital-skill complementarity, the contribution of capital service for the marginal product of skilled and unskilled labor is measured by
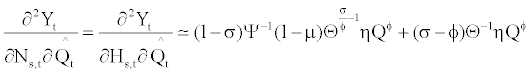 (33)
(33)
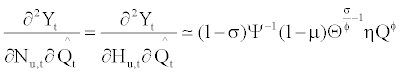 (34)
(34)
If we compare equations (34) and (33), then we can see that there is an additional term in equation (33): 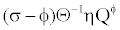 . Since σ>0 and ϕ<0 by assumption, the additional term is positive, which means that an increase in capital input enhances the productivity of skilled labor more than that of unskilled labor. As the complementarity between capital and skilled labor and the substitutability between capital and unskilled labor increase, (which is represented by a larger σ and a smaller ϕ) then the additional term in equation (33) becomes larger; therefore the labor demand becomes more biased toward skilled labor. On the other hand, if the complementarity and the substitutability decline (in other words, σ → 0 and ϕ → 0) and the production function approaches to the Cobb-Douglas form, then the additional contribution of capital diminishes.
. Since σ>0 and ϕ<0 by assumption, the additional term is positive, which means that an increase in capital input enhances the productivity of skilled labor more than that of unskilled labor. As the complementarity between capital and skilled labor and the substitutability between capital and unskilled labor increase, (which is represented by a larger σ and a smaller ϕ) then the additional term in equation (33) becomes larger; therefore the labor demand becomes more biased toward skilled labor. On the other hand, if the complementarity and the substitutability decline (in other words, σ → 0 and ϕ → 0) and the production function approaches to the Cobb-Douglas form, then the additional contribution of capital diminishes.
If a larger capital input stimulates the productivity of skilled labor more, then firms will demand more skilled workers than the unskilled ones, which will lead to an increase in the skill premium.
Sensitivity of the dynamics to the preference
Following Bils and Cho [9], we specify the disutility of labor supply as equation (2). They interpret the first term as the fixed cost of going to work and second term as the fixed cost of not enjoying leisure. Since the disutility is exactly compensated by the firm, we may regard it as the cost of hiring workers and their hours. With the calibration of φ=1.57 and ζ=2.00, Bils and Cho [9] assume that the worker is more reluctant to increase hours than weeks of work. The marginal cost of employment is mainly determined by the parameters φ and the marginal cost of hour by the parameter ζ. Therefore, the firm has to pay a higher marginal cost for additional hour than that for additional employment, which is reflected in the larger response of worker demand than that of hour demand to a shock. Considering that their calibration is based on the data up to the 1970s, the parameters may have been outdated. In particular, the marginal employment cost could have increased more than the marginal hour cost because of the increase in the benefit costs as discussed in Aaronson, et al [2].
We set the capital-skill complementarity as the second alternative model (σ=0.7 and ϕ=−2.0) and examine the response of employment and hour to a neutral and an investment- specific technology shock with different values of φ and ζ. Figures 16 and 17 describe the sensitivity of the dynamics. Column (a) shows the dynamics when φ=1.57 and ζ=2.00, which are the initial calibration. Columns (b) and (c) demonstrate the case where {2.00, 1.50} and {2.50, 1.00} are imposed on {φ, ζ}. The figure implies that as φ increases and ζ decreases, firms would rather adjust intensive margin of labor input than the extensive margin when they observe a positive technology shock: Compared to column (a), columns (b) and (c) show that the employments respond less while hours respond more. The dynamics of an investment-specific technology shock show a similar sensitivity as presented in Figure 17.
On the contrary, the dynamics of the relative wage are not sensitive to the preference parameters. As plotted in Figures 18 and 19, the impulse response of the relative wage does not change much with different sets of parameter values for {φ, ζ}. Since the increase in the employment cost is canceled out by the decrease in the hour cost, the response of the relative wage does not change much. Therefore we can conclude that the shape of the response is mainly determined by capital-skill complementarity.
This analysis implies that the change in the marginal employment cost may be one of the sources of jobless recovery, but is not likely to be the source of the hike in the skill premium.
When an economy is in a severe recession, the government cuts taxes and the central bank supplies more liquidity to boost output and employment. Those policies have been effective for job creation up till the 1980s but do not seem to be so after 1990. Some people named this situation “jobless recovery” and proposed several hypotheses to explain it.
This study focuses on the structural change in the production function and shows that the phenomenon of jobless recovery can be explained better without any assumption of nominal rigidity if we classify labor input by skilled and unskilled labor and impose capitalskill complementarity. In particular, we show that the job creation for unskilled worker after an investment-specific technology shock becomes more sluggish as capital-skill complementarity intensifies. Sluggish job creation in recent decades could be due to the fact that skilled labor has become more complementary to capital.
We can extend the model if we want make it relevant for monetary or fiscal policy analysis. First, we need to consider nominal rigidity to make the real variables respond to a monetary policy shock. It would be interesting to examine whether jobless recovery is observed to a positive monetary policy shock. On the other hand, as Shimer [18] notes, considering the labor adjustment cost in the model would be helpful to better explain jobless recovery. If we extend the model by incorporating those factors and find the estimates of the key parameters, either using two subsets of the sample, such as before and after 1990, or a time-varying parameter model as Kitagawa [19], then the extended model would work as a relevant one for macroeconomic policy analysis.
1Okun’s law implies that there is a linear relationship between output growth and unemployment. If jobless recovery becomes a typical phenomenon of economic recovery, then we may have to modify or discard Okun’s law.
2The typical economics textbook indicates that (structural) unemployment is coming from nominal rigidity, in particular, wage rigidity.
3The episode of 2001 is likely to be the result of an overinvestment in the 1990s.
4They define routine tasks by a limited and well-defined set of cognitive and manual activities which can be accomplished by following explicit rules, (e.g. record keeping, calculation, repetitive customer service, picking or sorting, and repetitive assembly). Nonroutine tasks are problem-solving and complex communication activities, (e.g. forming/testing hypothesis, medical diagnosis, and legal writing).
5The CES production function is a general form of production function which nests the standard Cobb-Douglas, linear, and Leontief production function. It is useful for this study because of its flexibility.
6Nordhaus claims that there has been more than a trillion fold decline in the real price of computing power.
7Fisher shows that the investment-specific shock and the neutral shock account for 38 percent and 80 percent of the fluctuation in hours and output after 1982. Furthermore, he finds that the investment-specific technology shock accounts for the majority of the effects.
8We can imagine a household composed of parents and children. Intuitively, we may suppose that the parents are well-educated and highly skilled, while the children are less skilled. Since we assume that the family members share the consumption goods equally, we do not need to consider the heterogeneous agent model.
9The steady state gross real interest rate will be equal to the inverse of the discount factor, i.e. 1+r=1/β. Assuming the average real interest rate (expressed as an annual frequency) is roughly two percent, a quarterly discount factor is about 0.995. The discount factor has to be adjusted for steady state growth, which amounts to roughly two percent per year or 0.005 per quarter. This gives us a discount factor of 0.995/1.005 = 0.99.
10Theoretically, the production function becomes the Cobb-Douglas form when σ and ϕ are zero. We impose very small numbers on the parameters because the model is not solvable when zeros are imposed.
11According to the calibration of Bils and Cho, the elasticity of the worker supply is higher than that of the hour supply. Since this calibration is based on data up till the 1970s, we will check the sensitivity of the result to the parameters.
12Because the production function is exhibiting a constant return to scale, the increase in the neutral technology by one percent implies that the productivity of every input factor increases by one percent.
13In the impact period, firm has to input more unskilled labor because the supply of capital service is limited. Thus the relative wage in the impact period declines. As the capital stock accumulates and the demand for capital and skilled labor increases, the relative wage increases.