Phase contrast technique employs the phase shift in the MR signal that is induced by the flowing blood in heart vessels. The merit of investigations on MR signals in heart disease treatments, heart tomographic imaging and discrimination between infracted, ischemic or normal myocardium has been early highlighted during the last decades through the works i.e. of Berman et al. [1,2] and Ingwall [3]. More recently, confirmation of accuracy and efficiently have been reported by several studies [4-8]. In this technique setup, blood spins moving along an applied gradient acquire a phase shift which is proportional to the strength and the duration of the gradient and the motion of the spins. In other terms, by applying two gradients, equal in duration and steepness but opposite polarity called bipolar gradients, a moving spin during the time the gradient is on, will either gain or lose a phase shift due to the motion in the increasing or decreasing magnetic field. This phase shift is proportional to the velocity of the moving spins, as long as the velocity of the spins is constant [9-11]. Thus the phase signal of stationary spins will be zero and this means that small heart arteries can be visualized, even with slowly moving blood. The phase shift of moving spins will be proportional to their constant velocity. The phase shift due to higher order motions, for example, acceleration, pulsation, etc, can be neglected under normal physiological condition. The errors of ignoring the higher order motions can be minimized by using short echo times (TE) especially in distributed flow.

The MRI signal at the sampling time t_s, induced by spin at the position r(t_s) which is excited by a slice selective radio frequency pulse given by:

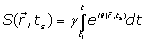    (1)

The phase 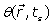of the MRI signal is:

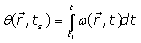    (2)

The Larmor frequency 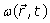and the main magnetic field 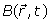are usually defined respectively as:

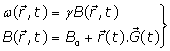     (3)

Where 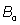is the static magnetic field, 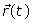is the spatial position and t₁is the time when spins are excited. By substitution of Eq. (1) into Eq. (2), the phase of the MRI signal becomes:

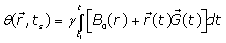      (4)

Since 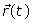is not constant for moving spins, 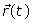 can be approximated in Eq. (4) by Taylors series as follows:

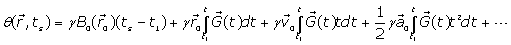     (5)

Where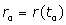: Position of spins,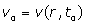: Blood flow velocity, 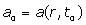: Blood flow acceleration (or deceleration) and 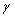= the gyro magnetic ratio of the hydrogen nucleus.

By setting a mono dimensional system, considering spatial dependence and setting a dimensionless time variable :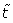

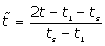     (6)

We have:

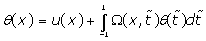    (7)

Where 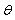 is the phase shift to be determined and  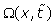is a pondering function defined, conjointly with the given function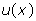, according to the system geometry (Figure 1):

Figure 1: Synopsis scheme of the modelled cardiac system.

The first term (the constant term) in Eq. (5) is induced by the main magnetic field 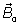and does not affect the reconstructed image. From the second term (the spatial term) the localization of the MRI signal is derived. The third term, also called the velocity term, contains the information about the instantaneous velocity of the spins. A careful estimation for the axial velocity component shows that the acceleration and the higher order terms can be neglected as long as the local acceleration of the blood flow remain physiological. On another hand, several magnetic resonance (MR) techniques have been based on the linearity between phase angle and velocity of moving blood in a gradient field as demonstrated by Meier et al. [12] , Bogren et al. [13,14] and Stahlberg et al. [15].

It is observed that the second term in Eq. (5) represents the phase shift due to the effects of the rF magnetic field. Traditionally, in any magnetic resonance imaging system we can consider the normalized magnetic field created conjointly by two similar circular coaxial conducting magnetic coils of radius R0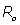, separated by a distance 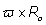(Figure 1), where 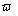is a positive real parameter. In this position NMR sensitive region is concentrated on the heart muscle along with the lower part of either inferior vena cava or lower coronary artery (according to field direction). For this geometry, we have [16-17]:

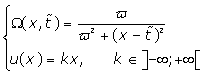       (8)

The proposed resolution protocol BPES begins by expressing phase shift θ(x) as a polynomial expansion:

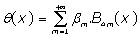      (9)

Truncated, as a physically accepted weak solution to:

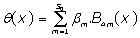       (10)

Where 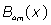are the 4m-order Boubaker polynomials (18-30), β_mare unknown coefficients and S₀ is a given integer.

By introducing Eq. (10) in Eq. (7), one obtains:

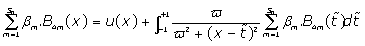     (11)

This is simplified to:

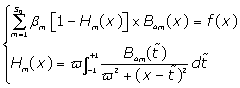        (12)

First,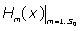 are calculated using the Boubaker polynomials properties detailed elsewhere [20-26] and in APPENDIX, then Eq. (11) is solved by determining the set 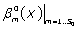which minimises the positive difference amount A:

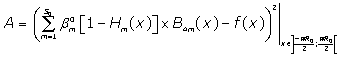
The solutions obtained in the particular case of 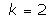, 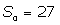and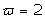

It could be noticed, in Figure 2, that the maximum phase shift is recorded in the central zone which corresponds to heart location, while at edges, where the tissue is absent, the phase shift is totally absent. This result in is in good agreement with the results proposed earlier by Johntson et al. [31], Chan et al. [32], Lethimonnier et al. [33] and Liu et al. [34].

Figure 2: Solutions, for k = 2, S₀ = 27 and ϖ = 2.

On another hand, it is known that normal heart tissue NMR relaxation times are approximately T₁=570 ms and T₂=57 ms. Since malignant tissues showed higher values of T₁ than normal tissue of same type, it is expected that phase shift profiles differ significantly between normal and i.e. ischemic heart. An appropriate NMR mapping, using the actual results along with those presented in the last decade’s literature (31-40) can yield good comparison patterns for identifying heart failure causes.

A solution to NMR diffusion partial differential equation derived from the Bloch NMR flow equations in a model of heart inferior coronary artery has been presented. Based on the Bloch NMR flow equations, we deduce analytical expressions to describe in detail the NMR transverse magnetizations and phase shift as a function of some NMR flow and geometrical parameters which are invaluable for the analysis of blood flow in heart vessels. The boundary conditions are inherently introduced based on the properties of the Boubaker polynomials expansion scheme BPES.

The most important conclusion to draw from the results of this mathematical formulation is that the NMR signal phase shift evaluation can be very a reliable guide to obtaining basic structural information on the heart dysfunction or anatomic defects.

The authors acknowledge the support from Federal University of Technology, Minna, Nigeria through the STEP B research program and the Swedish International Development Agency (SIDA) through the Abdus-Salam International Centre for Theoretical Physics (ICTP), Trieste, Italy.