B = Formation volume factor, dimensionless

c = Total compressibility, LT²M^-1

D = Mass fractal dimension, dimensionless

d = Euclidian dimension, dimensionless. d=2 in this study

FE = Flow efficiency, dimensionless

h = Thickness, L

k = Permeability

k_w = Permeability at the wellbore, L2

PI = Productivity index, L4TM-1

PI_n = Normalized productivity index

p = Pressure, M L^-1 T^-2

p_avg = Average pressure

q = Flow rate, L³ T^-1

r = Distance, L

r _D = Dimensionless distance

r_e = External radius of drainage area, L

r _w= Radius of wellbore, L

S = Skin factor, dimensionless

u = Heaviside step function

V_pD = Porev olume of drainage area

Greek Letters

β= Flow coefficient, dimensionless, see eq.(2)

φ = Porosity, Dimensionless

θ =Connectivity index, dimensionless

μ = Viscosity, L^-1T^-1M

Power-law rock properties may be due to an inconsistency between the computational space and the flow path. An actual flow domain may not fill the Euclidian space. The space excluded may be thought about as matrix and the fractional space filling property as embedding. A trivial example is a single vertical fracture or channel embedded in cylindrical computational space. More relevant, is a sparse fracture network. In both cases, the flow path fills only a fraction of the computational space. The degree of space filling may be characterized spatial dimension, D, which is a real number. For a fractal drainage area, the space filling dimension is the mass fractal dimension. Consider a Euclidian space of dimension d . The spatial dimension, d , is 1 for linear, 2 for cylindrical and 3 for spherical flow. The model depends on a single space variable, r.

The fracture network may or may not be characterized by fractal topology. We refer to a flow path as fractional when the spatial variable shows up as single term power-law functions in the diffusivity equation. This definition includes both the fractal and non-fractal case. In this study, all equations are formulated by use of fractal nomenclature.

Barker [1] proposed a generalized radial flow model (GRF) for geometries of any integer or non-integer space dimension. The concept was developed for a fracture network. Doe [2] pointed out that the fractional flow model includes non-fractured porous media.

Chang and Yortsos [3] proposed a fractal model to analyze reservoir behavior. Constant production in a fractal drainage area leads to pseudo-steady flow, Flamenco and Camacho-Velázquez [4]. simple algorithm to construct random fracture networks based on reservoir statistics, Acuna and Yortsos [5]. A realization may be used for visualization of the fracture network or for detailed local simulations by the finite element method. Deterministic simulations require detailed information which may impossible to achieve. Many realizations may be used for analysis by geostatistics. This technique is time consuming. An analytical model predicts the expected behavior quickly in an approximate way. The analytical solution gives insight into the interaction of the variables that a numerical one cannot provide. A disadvantage is that the analytical approach is restricted to simplified problems. Sometimes a simple model may be appropriate. For a new reservoir, there is not much information available. Hence a complex reservoir model may be of little value. Still wells have to be designed and drilled based on limited information. The main objective at this stage may be to establish a reasonable plateau period, production rate for the field and negotiate contracts.

A fractional reservoir model may be thought of as a generalization of the traditional homogeneous one. A space dimension may fall between the Euclidian space dimensions, 1, 2 and 3. We formulate the equations by use of fractal nomenclature. Suppose a fractal drainage area is embedded in a Euclidian space of dimension, d = 2 , which correspond to cylindrical geometry.

For pseudo-steady flow we have, Jelmert [6]:

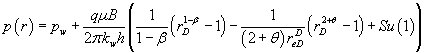              (1)

and for steady state flow, Jelmert [7]:

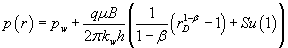              (2)

Where:

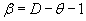              (3)

u is the Heaviside step function.

The difference between pseudo-steady and steady state flow rests with the second term on the right hand side of eq.(1).The boundary term is negligible when 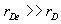.As a result, the equations for steady and pseudo-steady flow will usually coincide in the near wellbore region. Also, the pressure vs. distance profile has little sensitivity to the flow coefficient, â , in the near wellbore region, since r_D ≈1

Equation (1) and (2) has a singularity for β =1 . From L’Hospital’s

rule we find that: 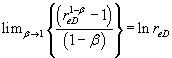. This result leads to flow equations, for pseudo-steady state and steady state, that are akin to the classical solutions for radial flow.

The skin factor, S, depends on the shape of the well. A line source (pseudo-cylindrical) well has been assumed. The skin may be visualized as a thin coating around the well. Pressure, at the wellbore side of the skin, is either decreased or boosted when fluid pass.

For steady state flow, the productivity index becomes, Jelmert [7]:

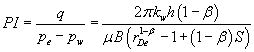            (4)

The characteristics of steady state flow have been extensively discussed in the above mentioned study.

The productivity index, PI, for pseudo-steady flow becomes:

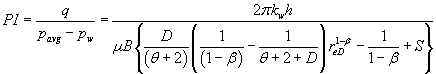            (5)

The productivity index is constant during steady- and pseudosteady flow. As a result, the production rate is proportional to PI. Improvements of the productivity index are of obvious importance. The traditional ways to accelerate production are stimulation and/or addition of wells (densification). The external radius, r_e, may be reduced by densification (infill drilling). The skin factor, S, may be reduced by stimulation: hydraulic fracturing, acid injection or explosives.

The productivity index depends on the unit system. Use of a normalized index will remove this inconvenience. The flow efficiency is defined as the ratio of the productivity indexes of a well with and without skin (Appendix B).

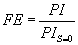            (6)

Combination of the above eq. (5) and eq. (6) yields:

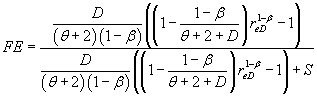            (7)

Hence FE <1 for a well with damage, S>0, FE >1 for stimulation, S<1, and FE =1 for S = 0 . The above equation may be used in the same way as for a homogeneous reservoir.

The flow efficiency is well suited to study the effect of the skin factor. To study the effect of β and θ , it may be better to normalize the productivity to the homogeneous reservoir productivity since the latter is independent of the fractal variables. The normalized productivity index is a measure of how much the actual reservoir deviates from the equivalent radial ideal homogeneous one (without skin).

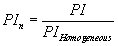            (8)

Index n denotes normalized. The rock properties at the reference distance are the same. In addition we assume that the fluid properties are characterized by a constant μB -product. The normalized productivity index will simplify to:

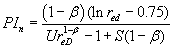            (9)

The coefficient U is:

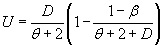            (10)

Under the assumptions of pseudo-steady state flow and that the external radius is large in comparison to the wellbore radius, it can be shown that, Jelmert [6]:

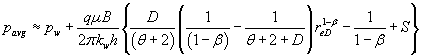            (11)

Furthermore:

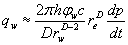            (12)

Integration of the above equation yields:

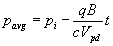            (13)

Where

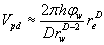            (14)

For the value D = 2 eq. (14) will simplify to the pore volume of a homogeneous reservoir.

Due to the assumption of constant derivative of pressure with respect to time, the difference between the average pressure and the wellbore pressure does not depend on time.

Substitution of eq. (13) into eq. (11) yields:

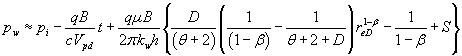            (15)

Equation(15) will plot as a straight with a slope that is inversely proportional to the compressibility-pore volume product. The slope gives rise to one equation which may be used to solve for one unknown, D or 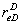. If one is known, the other may be estimated. The intercept with the vertical axis yields an additional equation which may be used to solve for another unknown. Determination of the variables: D, θ , and 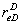, could also be estimated by data from other sources, well testing, logs outcrops etc.

We assume that the distance out to the outer boundary is,r_e , is 320 m and the radius of the well, r_w , is 10 cm. Figures 1 and 2 shows the pressure vs. distance profile for a positive and negative skin factor, S. Both plots are based on eq. (1).

Figure 1: Variation of pressure with distance

Figure 2:Variation of pressure with distance

The steady state solution, which is for perfect pressure support, is plotted as a broken line in Figure 1. The flow coefficient is less than unity, β = 0.9 and θ = 0.05 . From eq. (3) we obtain the fractal dimension, D =1.95. This case falls in the upper end of the region between the Euclidian dimensions d =1 and . These values correspond to linear and radial flow respectively. There is a discontinuity in pressure at the wellbore, r_D =1. The wellbore pressure, p_w, is located at the end of the vertical line. Note that the pressure in the reservoir plots as a straight line in the majority of the drainage area. The boundary term is important close to the external boundary.

Figure 2 shows the pressure vs. distance profile for β =1.05 and θ = 0.05 . The fractal dimension is D = 2.10 . This case falls between the Euclidian dimensions 2 and 3 which correspond to radial and spherical flow respectively. This case is possible, but rare. Note that the radial distance is increasing to the left. This is because the spatial term shows up with a negative exponent. The pressure profiles in Figures 1 and 2 are on the upper and lower side of the singularity at β =1 eq. (3).

There is little difference between the pressure profiles during pseudo-steady and steady state flow for this case. There is an important difference, however. The wellbore pressure, p_w, will remain constant for steady state flow but will decline according to eq. (15) for pseudosteady flow. Partial pressure support, which may be expected for an actual reservoir, will fall somewhere in between the ideal cases.

Figure 3 shows how much a fractional reservoir deviates from an equivalent homogeneous reservoir, eq. (8). The values β =1 and β = 0 are akin to radial and to linear flow respectively. One may speculate that the value in between, β = 0.5 , corresponds to bi-linear flow.

Figure 3: Normalized productivity index, vs. the flow coefficient, PI_nvs. β , eq. (8).

The poor performance at lower values of the flow coefficient, β , is striking. Doe’s areal interpretation may provide a straight forward explanation. In an equivalent traditional model the reservoir may be thought of as a single fracture of width ω . The source has the shape of a plane.

The steady state solution is given by eq.(2). For linear flow, β = 0, eq. (2) will reduce to:

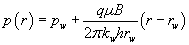            (16)

Direct integration of Darcy’s law for a channel of width ω and thickness h yields:

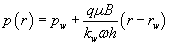            (17)

Equating the pressures under the assumption negligible skin factors yields the equivalent channel width:

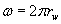            (18)

For a deep well the well bore radius is small, 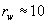cm. Hence, the equivalent width of the channel is 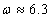cm. It is embedded in a circle which is large in comparison. The flow area of the channel is vanishingly small compared against the full circle. Poor performance must be expected. We believe that embedding a flow domain of low β -values in a cylindrical space leads to unreliable predictions. A better approach may be to sink the domain into a linear space, that is with Euclidian dimension d =1.

Another interesting feature of Figure 3 is that the normalized productivity index approach unity when the flow coefficient approaches one, 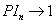as 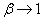. This suggests that the fractal solution includes a logarithmic productivity index as a limiting case. For 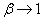we have 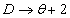, see eq. (3). A homogeneous reservoir has constant permeability and porosity. Hence, the traditional result depends on the additional requirement that D = 2 and θ = 0, see eq. (Appendix A). The interpretation is that the flow domain fills the Euclidian space with perfect connectivity. Under this assumption, the fractal model and the homogeneous one are identical.

Figure 4 shows the effect of the skin factor on the normalized productivity index. The figure illustrates that the advantage of reducing the skin factor is better for a small drainage area than a large one.

Figure 4: Normalized productivity index vs. Skin, PI_nvs. S , eq. (8).

The flow efficiency, FE, is given by eq. (6). Figure 5 shows the advantage of reducing the skin factor. For negative skin values, the effect of a reduction is better for higher values of the flow coefficient than lower ones. For positive skin factors, it is the other way around.

Figure 5: Flow Efficiency vs. skin, FE vs. S , eq. (6).

From eq. (4) obtain:

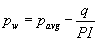            (19)

A pressure vs. rate plot is a useful tool to analyze the behavior of wells. The productivity index, PI , show up as the slope between a straight line and the vertical axis. Figure 6 shows the inflow performance relationship for various values of β and θ . The upper line is clearly the best since it will give the highest production rate for a given drawdown.

Figure 6: Inflow performance.

The straight line behavior in Figure 6 is the consequence of pseudosteady flow, not the actual reservoir model. Hence, observed behavior may be matched to any reservoir model under pseudo-steady flow. Use of a simplistic (homogeneous) model calibrated to observed behavior may be unproblematic as long as no changes in the operating conditions are needed. Once changes are required, the most realistic (embedded fracture network) model will provide a better understanding of the problem.

Generalized reservoir inflow equations based on the productivity index have been proposed. It is valid for, but not limited, to fractal reservoirs. The proposed model may highlight problems that may go undetected by the traditional one. The equations discussed are valid during pseudo-steady state flow.

It is possible to obtain the pore volume by reservoir limit testing.

The proposed model has two additional parameters when compared against the traditional one. The solution switches from power-law to logarithmic type when the flow unit parameter, β =1 . There is a smooth transition over the singularity. The generalized pseudo-steady state model will for all practical purposes reduce to the traditional one for D = 2 and θ = 0.

The productivity may be improved by infill drilling and stimulation.