Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2014) Volume 4, Issue 1
When investigating the regeneration or development of a city, taking into consideration the urban environment is an important point for investigation. The increasingly apparent damage and deterioration of human health, owing to the worsening of the thermal environment in cities caused by heat islands, has made the economic need to improve the urban thermal environment an urgent requirement. As a method of quantifying the results of improving the urban thermal environment for the population, the urban environment can be evaluated by the sensational and physiological temperature. Quantifying the amount of heat transfer from the environment to humans, and clarifying the effects on human physiology and psychology are important. The physical values related to autonomic and behavioral thermoregulation and climatic and environment factors, in spaces occupied by humans are essential.
Values related to the meteorological environment and behavioral thermoregulation can be measured or estimated within a certain range. However, values related to autonomic thermoregulation are difficult to identify. For example, the only methods available for estimating the result of physiological responses of the body exposed to the environment, expressed as skin temperature, is to take measurements, or to use a developed thermoregulation model, which assumes that the body is “floating” within a room.
Conventional research that captures the relation between thermal environmental conditions and the human response has been carried by laboratory measurement. Laboratory measurements are performed in a place where environmental and human conditions are easy to control. A wide range of thermal environments — such as an office space as opposed to a technician-controlled laboratory; a living-room space in which movement is freely controllable over a wide range as opposed to the office space; and the thermally uncomfortable outdoors, in which one’s place and point of focus can be changed at will — are considered to be preferable. Therefore, it is necessary to evaluate the thermal environment with regard to behavioral thermoregulation; that is to say, investigating different postures, from seated to standing, is essential.
The majority of research, which investigates the influence on human responses in indoor spaces, studies the seated position of the subject, and it is rare to find a case where heat conduction has been considered for thermal environment evaluation or body heat balance. In spaces with air-conditioning, which uses thermal radiation or conduction, the space between the body and the heating surface becomes close, and the heat transfer area of the thermal radiation source (for example, heated flooring) becomes large. In addition, the heat transfer area on the body side is large for seated or supine postures, which have a large surface area in contact with the floor [1]. Therefore, the influence of heat conduction or thermal radiation is difficult to ignore, and the effect of thermal sensation and thermal comfort on the human body becomes stronger, when compared to a space controlled only at air temperature. Kurazumi et al. [2,3] verified the posture, which considers the effect of heat transfer, and it was clear that it was necessary to make an evaluation of the conductive heat transfer area between the floor and the body, when in lying or floor-seated positions. However, it is rare to find research encompassing the body heat balance which considers heat transfer. This then is the reason for the non-clarification of the necessary body system values to calculate the body’s heat balance [4,5], as well as the lack of thermal environment evaluation indices affected by heat transfer.
Focusing on this point, Kurazumi et al. [6] developed the Conduction-corrected modified effective temperature (ETF), which includes heat conduction, in order to be able to evaluate the thermal environment in the living space in which behavioral thermoregulation changes with posture. This sensational and physiological temperature index ETF can take into account the effect of factors such as: air velocity, long-wave radiation, heat conduction, and humidity. Moreover, each temperature-“converted” factor can further calculate the temperature, making possible a same-axis evaluation of the overall and individual effects of environment factors on thermal sensation. This thermal environment evaluation factor ETF for the living-room space can be evaluated for different postures of behavioral thermoregulation. Furthermore, verification experiments were carried out to confirm the relation between ETF and the physiological and psychological effects on the human body, and the effectiveness as a living environment evaluation factor, including heat conduction from the floor, for a living space [7-9]. In these verification experiments, the heat conduction was shown to have a great effect as environmental factors which contribute to the ETF.
In outdoor spaces in the summer, the sensational and physiological temperature rises, owing to the influence of heat conduction, which makes heated road surfaces too hot to touch directly. However, sensational and physiological temperature lowers, as a result of the influence of heat conduction, when sat on the ground with a ground cover or on shaded ground. Therefore, it is necessary to consider the effect of short-wave solar radiation on the body’s heat balance. It is also necessary to include the influence of heat conduction on sensational and physiological temperature for outdoor spaces.
Focusing on this point, Kurazumi et al. [10] developed the Enhanced conduction-corrected modified effective temperature (ETFe) which includes the influence of heat conduction and solar radiation in an outdoor space. ETFe can account for the effect of factors, such as different postures, air velocity, long-wave radiation, short-wave solar radiation, heat conduction and humidity. Moreover, each temperature- “converted” factor can further calculate the temperature, making possible a same-axis evaluation of the overall and individual effects of environmental factors on thermal sense in an outdoor space. ETFe can evaluate the effect of different postures on behavioral thermoregulation in outdoor spaces. Furthermore, verification experiments have been carried out to confirm the relation between ETFe and the physiological and psychological effects on the human body, and its effectiveness as an outdoor environment evaluation factor, including heat conduction from the ground for an outdoor space, has been confirmed [11]. In these verification experiments, heat transfer and short-wave solar radiation were shown to have as great effect an as environmental factors which contribute to the ETF. Kurazumi et al. [12] considered the comfort range for outdoor space to be ETFe of 31.6–38.5°C.
As mentioned above, in order to obtain the ETF [6] or ETFe [10], the skin temperature of a human is required for body heat balance. This physiological factor must be obtained through actual measurements. However, simulation of the thermal environment makes these actual measurements impossible. In addition, a great thermal strain is placed on the subject in outdoor spaces. Therefore, it is necessary to make simulated calculations of skin temperature as a human’s physiological response.
There are various models that have been developed to characterize the thermoregulation of humans, which measure the physiological factors of humans. There is the relatively simplified Wissler cylinder model [13], Atkins and Wyndham [14] revised the Wissler model, and there is also Gagge et al.’s Two-Node Model [15-17]. Those which take into account the human shape include Stolwijk and Hardy [18], Stolwijk [19], Smith [20], Takemori et al. [21], Fu [22], Yokoyama et al. [23-25], Tanabe et al. [26], Huizenga et al. [27], McGuffin et al. [28], Kohri and Mochida [29], Ozeki et al. [30], Sakoi et al. [31], and Kuwabara et al. [32]. These have been developed to allow for the evaluation of nonuniform environments, and non-steady-state environments.
From the above things, when examining the heat balance of the body, it is necessary to include short-wave solar radiation and heat transfer. With regard to short-wave solar radiation, the thermoregulation model of Kuwabara et al. [32] is included. Without separating short-wave solar radiation and long-wave radiation, a thermoregulation model has been developed for a uniform thermal space that includes shortwave solar radiation. However, heat conduction is not included in any thermoregulation model.
Focusing on this point, Kurazumi et al. [33] developed the thermoregulation model for evaluation of the heat conduction and the solar radiation, in the perimeter zone of office buildings and livingspace environments. To verify this model, experiments were conducted. The Kurazumi model [33], which includes short-wave solar radiation and heat conduction, is considered to be adaptable to the perimeter zone of office and living-space thermal environments. However, this model does not assume that the thermal neutral temperature is much lower than the thermal environment for an indoor environment, since the difference from the actual value in a low temperature environment, in which the blood vessel contraction coefficient is small, is considered to be large. Also, in a low temperature environment, shivering heat production is assumed to be a steady state expression.
Thus, this study measured the thermoregulation response of the human body when changing postures, during behavioral thermoregulation in an outdoor space. In order to make a possible evaluation of the thermal environment of an outdoor space, a thermoregulation model was developed, which included the thermal influence owing to heat conduction, short-wave solar radiation and long-wave radiation, and is based on the Kurazumi model [33], which is an improved Two-Node Model [17], the validity of which has already been confirmed.
Then, in order to verify the effectiveness of this thermoregulation model as a simulation model, it was necessary to clarify the relation between the analytical solutions of this behavioral thermoregulation in an outdoor space and the physiological response of the human body. Therefore, in order to verify the validity of this thermoregulation model, experiments using subjects were conducted.
The Kurazumi model [33] is a two-layer model formed from a body core and an outer shell. This model can calculate the heat balance and control signals for each layer, and predict the heat loss, owing to skin temperature and body core temperature, and perspiration given the body’s clothing factor and metabolism, as well as environmental conditions: air temperature, humidity, air velocity and mean radiant temperature. The time spent in an outdoor environment is short, and there are many cases of transitions between non-steady conditions. Then, by considering behavioral thermoregulation, the final aim is to improve or expand into models which assume non-steady state, or into thermoregulation models, taking into account the human body’s geometry.
However, many human factors for each posture or body section have still not been measured or verified. Moreover, the sensational and physiological temperature indices are developed for the whole body. Thus, the aim is to improve or expand the simple models that quantify the whole body.
The Kurazumi model [33] used in this study is a thermoregulation model of a simple form, assuming steady state. In order to know the physiological response of the human body in an outdoor environment and its positions, the same simple model was improved and expanded.
Behavioral thermoregulation model
In the Two-Node Model, the body is assumed to be a single sphere, divided into a skin layer and a core layer, with internal heat transfer, and heat transfer between the body and the environment. However, an outdoor space differs from an indoor space, and the influence of direct solar radiation on heterogeneous and asymmetric systems is remarkably strong. Therefore, to investigate the heat conduction owing to behavioral thermoregulation, or the heat exchange owing to shortwave solar radiation, it is essential to split the modeling into segments that receive solar radiation directly, segments that receive solar radiation indirectly through reflection or scattering, and segments that receive heat conduction. Then, in order to be further improved, the thermoregulation model was expanded into 6 layers, formed from each of the segments (Figure 1).
Figure 1: Diagram of behavioral thermoregulation model in outdoor. Cv is convective heat exchange at skin. RS is short-wave solar radiation heat gain on human body. Rsh is sky radiation on human body. Rrf is reflected solar radiation on human body. RL is long-wave radiation heat loss from human body. Cv is convective exchange at skin. Cd is conductive exchange at skin. E is evaporative heat loss from skin. Hres is respirational heat loss. fcl is effective surface area factor of clothing. Fcl is thermal efficiency factor of clothing. Fpcl is permeation efficiency factor of clothing. Fcld is thermal efficiency factor of clothing. fp is projected area factor. fcond is conductive heat transfer area factor. Tcrs is core temperature of direct solar radiation part. Tsks is skin temperature of direct solar radiation part. Tcrl is core temperature of indirect solar radiation part. Tskl is skin temperature of indirect solar radiation part. Tcrd is core temperature of heat conduction part. Tskd is skin temperature of heat conduction part.
Based on the Two-Node model, the heat produced by metabolism (necessary for activity and shivering), the heat loss owing to breathing, the thermoregulatory control of sweating, skin blood flow etc., were made proportional to the heat transfer area factor for each direct solar radiation segment, the indirect solar radiation segment, and the heat conduction segment. However, the heat conduction segment was assumed not to produce the thermoregulatory control of sweating.
Handling of Solar Radiation in an outdoor environment
Air temperature, humidity, air velocity and surface temperature can be used as physical quantities, without conversion into separate units for calculating each kind of thermal environment evaluation index. However, some kind of conversion must be performed on solar radiation for it to be used.
Solar radiation is treated as a short-wave solar radiation heat gain. The solar radiation (solar constant) that arrives in the Earth’s atmosphere can be separated into direct solar radiation that propagates directly through the atmosphere and arrives as parallel rays, diffuse solar radiation that is scattered by the atmosphere and arrives from the sky, and reflected solar radiation that arrives after being reflected by the Earth’s surface and surface features; i.e. buildings etc. From within these, the combination of direct and diffuse solar radiation is the total solar radiation, which is usually measured as the downward quantity of total solar radiation.
The specific handling method for solar radiation is to separate the vertical quantity of total solar radiation into direct and diffuse solar radiation, and to seek these components. Next, the direct solar radiation on human body is sought using the projected area factor of the human body, corresponding to the solar altitude. Then, the sky is treated as a perfect diffusing surface, and the sky radiation on the human body is calculated using the angle factor between the human body and the sky. The reflected solar radiation on the human body is calculated using albedo and the angle factor between the human body and surface features. Accordingly, short-wave solar radiation heat gains can be expressed by the following equations:
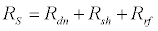 (1)
(1)
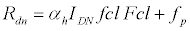 (2)
(2)
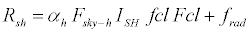 (3)
(3)
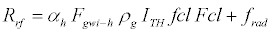 (4)
(4)
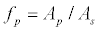 (5)
(5)
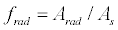 (6)
(6)
In calculating the reflected solar radiation from surface features, the area of the surface features receiving the radiation, and the direct and diffuse solar radiation etc. on it, are indispensable. However, the specification of these physical quantities is exceedingly difficult. Accordingly, the surface features are treated as having the same reflectance as the Earth’s surface in this research. Namely, the human body is considered as existing in an open space enclosed by the sky and the ground surface. Consequently, the reflected solar radiation on the human body can be expressed by the following equations:
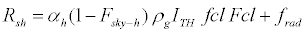 (7)
(7)
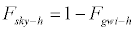 (8)
(8)
The consideration of long-wave radiation together with short-wave solar radiation is indispensable for the radiant heat exchange between the human body and the environment, for an outdoor space. Longwave radiation is a heat exchange between the human body and the Earth’s surface/surface features/sky. Accordingly, long-wave radiation heat loss can be expressed by the following equations:
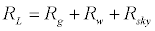 (9)
(9)
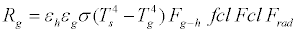 (10)
(10)
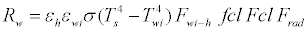 (11)
(11)
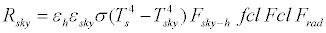 (12)
(12)
In this research, seeking and estimating the surface temperature of surface features in an open space through actual measurements is exceedingly difficult. Accordingly, the surface temperature and emissivity of surface features are treated in the same way as that of the Earth’s surface in this research. The radiant heat from the human body to the Earth’s surface and surface features can be expressed by the following equation:
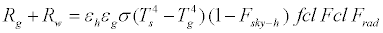 (13)
(13)
Long-wave radiation heat loss and short-wave solar radiation heat gain are treated separately and independently, and the effect of each one on the human body is made clear. By considering the human body to be enclosed in long-wave thermal radiation environment in the outdoor space, with a uniform mean radiant temperature and radiant heat transfer coefficient, the mean radiant temperature and the radiant heat transfer coefficient of the outdoor space can be expressed by the following equations:
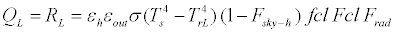

 (14)
(14)
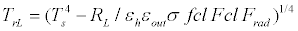 (15)
(15)
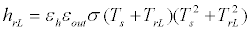 (16)
(16)
As when specifying the long-wave radiant heat balance in an indoor space, it is important to specify the long-wave radiation heat loss and short-wave solar radiation heat gain in an outdoor space.
This is a similar issue for other general indoor environment evaluation indices, based on the heat balance of the human body. By calculating numerical values based on actual measurements of these heat balances, using long-wave and short-wave net radiometers, it is possible to treat all of the primary factors as a mean-value modeled condition. In case measurements cannot be made, the surface temperature and emissivity of the surface feature are treated as equivalent to that of the Earth’s surface. Also, the heat transfer from individual environmental elements considered to have a strong degree of influence is separated from other environmental elements, and calculated individually using the angle factor.
Handling of heat conduction in an outdoor environment
The quantity of heat exchange, owing to conduction between the human body and a contact surface, can be expressed by the following equation outdoors:
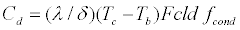 (17)
(17)
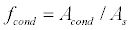 (18)
(18)
To measure heat flow, the following equation is used:
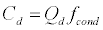 (19)
(19)
Applying equation 18, which reflects the resultant heat conductance hd [6], to equation 21, and rewriting it gives equation 20:
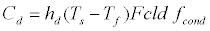 (20)
(20)
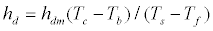 (21)
(21)
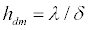 (22)
(22)
To measure the heat flow, the following equation is used:
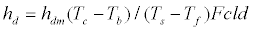 (23)
(23)
Body heat balance of the human body
In an outdoor environment, thermoregulation model’s body heat balance of each compartment can be expressed as follows. The body heat balance of the direct solar radiation segment of the core layer can be expressed by the following equation:
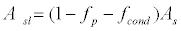 (24)
(24)
Moreover, in the case of the Two-Node Model used as the foundation of this model, under the thermal condition where body temperature is reduced, the ratio of body weight of skin layer α is raised, and the ratio of body weight of core layer is lowered. In contrast, under the thermal condition that body temperature is increased, the ratio of body weight of skin layer α is lowered, and the ratio of body weight of core layer is raised. This mechanism is included in the Two- Node Model. In the actual human body, in a cold environment, core temperature is maintained by means of the thermal resistance between the core and skin layers, which depends on the variations of the body weight of the skin layer. In contrast, in a hot environment, it is easy to lose the core temperature. However, it does not include the variations by ratio of the body weight of the skin layer α and the heat conductance between the skin and core layer kmin in the Two-Node Model. Therefore, the model formula by ratio of body weight of skin layer α of heat conductance between skin and core layer kmin is included in the new revised model of the Two-Node Model.
The ratio of body weight of skin layer α, heat conductance between skin and core layer kmin, and equivalent length between skin and core layer lmin, in an equilibrium of core and skin temperatures, is expressed as αn, kn, and ln, respectively. Since heat conductance between skin and core layer kmin is inversely proportional to the equivalent length between skin and core layer lmin, the heat conductance between the skin and core layer kmin can be expressed by the following equation:
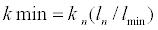 (25)
(25)
It is assumed that the human body is regarded as a sphere in the Two-Node Model. The relation among ratio of body weight of skin layer α, equivalent sphere radius of human body core layer rcore, and equivalent sphere radius of skin layer to the human body rskin, can be expressed by the following equation:
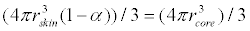 (26)
(26)
Applying equation 26, the equivalent sphere radius of human body core layer rcore can be expressed by the following equation:
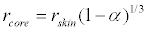 (27)
(27)
The equivalent length between the skin and core layer lmin is the difference between the equivalent sphere radius of the skin layer of the human body rskin and the equivalent sphere radius of human body core layer rcore. Thus, the equivalent length between skin and core layer lmin can be expressed by the following equation:
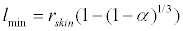 (28)
(28)
Similarly, it is assumed that the ratio of body weight of skin layer under neutral condition is β, so equivalent length between skin and core layer under neutral condition ln can be expressed by the following equation:
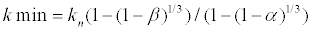 (29)
(29)
Applying equation 28 and 29 to equation 25, the heat conductance between skin and core layer kmin can be expressed by the following equation:
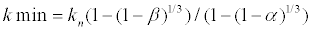 (30)
(30)
However, in the present situation, the heat conductance between the skin and core layer in a neutral condition kn is still unknown. Thus, in this study, it only expresses the model formula by ratio of body weight of skin layer α of heat conductance between skin and core layer kmin. In the Two-Node Model, the heat conductance between skin and core layer, kmin, does not depend on the ratio of body weight of the skin layer α. That is to say, heat conductance between the skin and core layer kmin is a constant.
Body heat balance for the indirect solar radiation segment of the core layer can be expressed by the following equations:
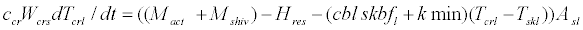 (31)
(31)
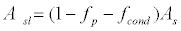 (32)
(32)
Body heat balance for the heat conduction segment of the core layer can be expressed by the following equation:
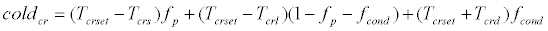 (33)
(33)
Body heat balance for direct solar radiation segment of the skin layer can be expressed by the following equation:
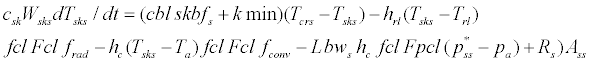 (34)
(34)
Body heat balance for the indirect solar radiation segment of the skin layer can be expressed by the following equation:
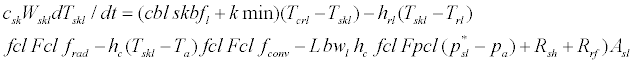 (35)
(35)
Body heat balance for the heat conduction segment of the skin layer can be expressed by the following equation:
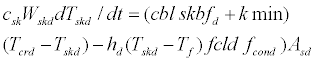 (36)
(36)
Controlling system in body temperature regulation
In the thermoregulation model for an outdoor space, which includes heat conduction and short-wave solar radiation, the thermoregulation signal from direct solar radiation, indirect solar radiation and heat transfer segments are separated, and weightings are assigned, according to the difference between the core layer temperature and skin layer temperature for each segment, and the set-point temperature for each segment from the heat transfer area factor. Then, this is made to be the core layer thermoregulation signal.
Thermoregulation signals of core layer can be expressed by the following equations:
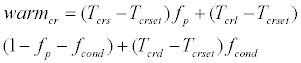 (37)
(37)
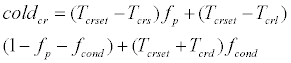 (38)
(38)
If warmcr<0, it is referred to as warmcr=0. Similarly, if coldcr<0, it is referred to as coldcr=0. Thermoregulation signals of the skin layer can be expressed as follows:
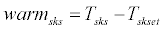 (39)
(39)
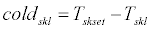 (40)
(40)
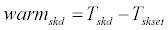 (41)
(41)
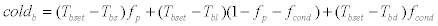 (42)
(42)
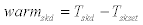 (43)
(43)
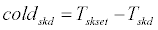 (44)
(44)
If warmsks<0, it is referred to as warmsk=0. Similarly, if warmskl<0, it is referred to as warmskl=0; if warmskd<0, it is referred to as warmskd=0; if coldsks<0, it is referred to as coldsks=0; if coldskl<0, it is referred to as coldskl=0; if coldskd<0, it is referred to as coldskd=0.
Thermoregulation signals of the body temperature can be expressed by the following equations:
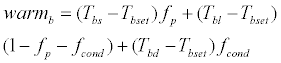 (45)
(45)
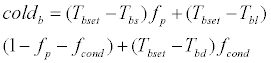 (46)
(46)
If warmb<0, it is referred to as warmb=0. Similarly, if coldb<0, it is referred to as coldb=0.
Thermal influence of behavioral thermoregulation
As mentioned in the purpose of this study, posture was focused upon as the result of behavioral thermoregulation. Therefore, the thermal influence of behavioral thermoregulation is expressed as the change in body system factors owing to posture. The changing body system factors were taken as heat transfer area factors (projected area factor, convective heat transfer area factor, radiant heat transfer area factor, conductive heat transfer area factor), and heat transfer coefficients (convective heat transfer coefficient, radiant heat transfer coefficient, resultant heat conductance [6], effective surface area of clothing, thermal efficiency factor of clothing, thermal efficiency factor of clothing in heat conduction segment, angle factor of the human body.
Verification of Mean Skin Temperature by Behavioral Thermoregulation Model
Experimental design
The measurements were carried out in winter, from January to March, and in summer, from July until October. Figure 2 shows the measurement region. The observation points are in an urban area adjoined by educational and commercial districts in Nagoya, Japan. A forest of 410 ha remains as an urban green zone in the vicinity of the measurement region and there is a zoo adjoining. Summary of the observation point is shown in Table 1. For the measurements, observation points were selected with consideration for the condition of the ground surface, such as bare ground, where the surface is gravel or soil, paved ground such as concrete, asphalt or blocks, green areas covered in plants and water surfaces, and with consideration for the sky factor owing to buildings or trees etc. In total, fifteen observation points were chosen.
| Experimental Season | Point | Survey site | Ground surface | Skywards surface | Surrounds North side | Surrounds East side | Surrounds South side | Surrounds West side | Sky factor | Green factor |
|---|---|---|---|---|---|---|---|---|---|---|
| Winter | 1 | University campus | Paving brick | Open | Open | Open | Building | Building | 0.819 | 0.005 |
| Winter | 2 | Building canyon | Concrete | Roof | Open | Open | Building | Building | 0.323 | 0.004 |
| Winter | 3 | Building side | Concrete | Open | Open | Open | Building | Building | 0.443 | 0.000 |
| Winter | 4 | Residential street | Asphalt | Open | Building | Open | Wall | Open | 0.701 | 0.021 |
| Winter | 5 | Community playground | Bare ground | Open | Tree | Tree | Tree | Tree | 0.861 | 0.015 |
| Winter | 6 | Park green area | Dead grass | Tree | Tree | Tree | Tree | Tree | 0.766 | 0.361 |
| Winter | 7 | Community park | Dead weed | Tree | Tree | Tree | Tree | Tree | 0.632 | 0.300 |
| Winter | 8 | Park road | Asphalt | Tree | Open | Tree | Open | Wall & Tree | 0.497 | 0.207 |
| Winter | 9 | Parking | Asphalt&Reservoir | Open | Open | Open | Open | Open | 0.978 | 0.055 |
| Winter | 10 | Roadeside | Pavingbrick | Tree | Tree | Open | Tree | Open | 0.570 | 0.100 |
| Winter | 11 | Templeprecincts | Gravel | Open | Building | Open | Open | Slope | 0.809 | 0.036 |
| Winter | 12 | Promenade | Asphalt | Bamboo | Open | Bamboo | Open | Bamboo | 0.447 | 0.269 |
| Winter | 13 | Urban canyon | Pavingtile | Roof | Open | Building | Open | Building | 0.482 | 0.007 |
| Winter | 14 | Promenade | Woodendeck | Open | Open | Building | Open | Open | 0.734 | 0.033 |
| Winter | 15 | Universitypark | Brick&Grass &Pond | Open | Tree | Tree | Building | Tree | 0.340 | 0.258 |
| Summer | 1 | Universitycampus | Pavingbrick | Open | Open | Open | Building | Building | 0.712 | 0.013 |
| Summer | 2 | Buildingcanyon | Concrete | Roof | Open | Open | Building | Building | 0.271 | 0.021 |
| Summer | 3 | Buildingside | Concrete | Open | Open | Open | Building | Building | 0.413 | 0.000 |
| Summer | 4 | Residentialstreet | Asphalt | Open | Building | Open | Wall&Grass | Open | 0.532 | 0.132 |
| Summer | 5 | Communityplayground | Bareground | Open | Tree | Tree | Tree | Tree | 0.824 | 0.092 |
| Summer | 6 | Park greenarea | Grass | Tree | Tree | Tree | Tree | Tree | 0.467 | 0.654 |
| Summer | 7 | Communitypark | Weed | Tree | Tree | Tree | Tree | Tree | 0.091 | 0.815 |
| Summer | 8 | Park road | Asphalt | Tree | Open | Tree | Open | Wall&Tree | 0.240 | 0.377 |
| Summer | 9 | Parking | Asphalt&Reservoir | Open | Open | Open | Open | Open | 0.936 | 0.108 |
| Summer | 10 | Roadeside | Pavingbrick | Tree | Tree | Open | Tree | Open | 0.210 | 0.313 |
| Summer | 11 | Templeprecincts | Gravel | Open | Building | Open | Open | Slope | 0.797 | 0.079 |
| Summer | 12 | Promenade | Asphalt&Weed | Bamboo | Open | Bamboo | Open | Bamboo | 0.322 | 0.578 |
| Summer | 13 | Urban canyon | Pavingtile | Roof | Open | Building | Open | Building | 0.298 | 0.047 |
| Summer | 14 | Promenade | Woodendeck | Open | Open | Building | Open | Open | 0.608 | 0.095 |
| Summer | 15 | Universitypark | Brick&Grass &Pond | Open | Tree | Tree | Building | Tree | 0.383 | 0.401 |
Table 1: Summary of observation points.
Mobile measurements were carried out on foot. A trolley was used to transport the thermal environment measuring instrument. The movement speed was slower than walking speed: around 0.7m/s. The selected observation points were chosen at random, and the routes to the points were undecided. With consideration for the burden on subjects, the experiment was concluded at a point two hours after commencement of the mobile observations.
In indoor spaces, such as laboratory experiments, it is exceedingly rare to test the subject in extremely hot or cold thermal environments. In general, in experiments that include a transition period or an uneven thermal environment, the exposure experiment time period is the subject of the investigation, such that the heat balance between the human body and the environment becomes almost steady state. However, the thermal environment of summer outdoor spaces can be harsh, to the extent that there are cases of deaths owing to heatstroke, whilst the thermal environment of winter outdoor spaces can be harsh, to the extent that the body temperature drops to the zone of body cooling. Accordingly, one must avoid extended periods in outdoor spaces where one would be struck by direct solar radiation in a high temperature environment, or by strong winds in a low temperature environment. It is unavoidable that experiments on subjects in outdoor spaces treat a necessary short transition period. As a result, out of consideration for the subjects’ maintenance of a standing position and the response time of the Assman ventilated psychrometer, the actual measurement on the human body response and thermal environment in the mobile observations was performed after having established the observation device and leaving it for five minutes. Naturally, it can be conjectured that the human body response will differ the longer the exposure time of the subjects. However, the experimental period was determined with consideration for the safety of the subjects. Unlike an indoor space, it is difficult to consider spending extended periods in an outdoor thermal environment that can be considered uncomfortable, owing to behavioral thermoregulation by means of environmental refuge behavior.
Subjects moved on foot to the observation point after having been seated and at rest for 60 minutes or longer in an indoor air-conditioned space (reference point 0 shown in Figure 2). In the winter, the room temperature and humidity were set 22ºC and 40%, respectively. And, in the summer, the room temperature and humidity were set 28ºC and 60%, respectively. The migration speed of the subjects was around 0.7 m/s, owing to following the movement of the trolley in which the experiment staff transported the measurement instruments.
After arriving at each measurement point, the subjects stood in a standing posture for five minutes, including the time in which the experiment staff was setting up the measurement instruments for the thermal environment, and the preparations for the measurement. Thereafter, the subjects were exposed to the thermal environment in a standing posture for five minutes, as discussed above. The subjects were positioned around 1.5 m away from the center of the thermal environment measurement spot, in a location where the solar radiation was not obstructed, or the thermal environment measurement instruments were not surrounded. After five minutes’ exposure, the subjects reported the average thermal comfort and average thermal sensation for the whole body that they experienced for the time period.
Air temperature, humidity, air velocity, short-wave solar-radiation heat quantity, long-wave radiation heat quantity, ground surface temperature, and water surface temperature were measured. The air temperature and humidity were measured at 0.9 m height above the ground, by means of an Assmann ventilated psychrometer. The average air velocity was measured for five minutes at a height of 1.2 m above the ground, by an omni-directional anemometer (Kanomax Japan, Inc.: 6533, measurement range 0.05~5.00 m/s). The short-wave thermal radiation heat quantity, in the regions from the visible to the near-andmid- infrared, and the terrestrial thermal radiation in the far infrared region, thermal radiation heat quantities downwards and upwards, were measured at a height of 0.9m above the ground, by long- and shortwave radiometer (EKO Instruments: MR-50, sensitivity 7μV/Wm-2, short-wave range 305~2800 nm, long-wave range 5000~50000 nm). The ground surface temperature and the water surface temperature were measured by a radiation thermometer (KONICA MINOLTA: HT-10D, measurement wave 8~14 μm, measurement angle 1.4~2º, emissivity measurement range 0.10~1.00).
The sky factor was measured by a photograph of the sky taken 1.2 m above the ground at the observation point, using a fish-eye lens with an orthographical projection format (Nikon: OP Fisheye Nikkor 10 mm f/5.6), and a 35 mm digital SLR camera. The ratio of green, water surface solid angles to celestial globe solid angle was measured by a photograph of the sky, taken 1.2m above the ground at the observation point, using a fish-eye lens with an equisolid angle projection format (Olympus: Fisheye Zuiko 8 mm f/2.8), and a 35 mm digital SLR camera. The albedo, sky temperature, and surface temperature were calculated from each directional component of the short-wave thermal radiation heat quantity, and the long-wave thermal radiation heat quantity.
Skin temperatures were measured as physiological conditions for the human body. Skin temperature exposed to the atmosphere was measured at the positions of the head, trunk, arm, hand, thigh, lower leg and foot. Skin temperature for ground contact was measured at the sole of foot. Skin temperatures of body parts exposed to the atmosphere were measured by a thermistor thermometer (NIKKISO-THERM, N542R and ITP8391, measurement range -50~230ºC, resolution 0.01ºC). Skin temperature for ground contact was measured as a physiological condition of the human body by a thermal flux sensor (Captec Entreprise, HF series, 0.4 mm thick, sensitivity 1.69~2.10 mV/ (W/m2), response time, 200 ms, one side painted black). It contained T-type thermocouples. The subjects selected their clothing freely, suitable for the weather on the measurement day. The clothing quantity of the subjects was calculated by the clo value, by layering the clothing reported by the subjects [34].
Subjects
The subjects were 11 healthy young females. The physical data for the subjects is shown in Table 2. The age was 21.0 ± 0.6, their height was 1.568 ± 0.026 m, and their weight was 50.2 ± 5.1kg. The BMI was 20.4 ± 1.9. Thus, they are considered to not be subjects of a unique physique.
| Subject | Sex | Age | Height (cm) | Weight (kg) | B-area (m2) | Rohrer Index | Native land |
|---|---|---|---|---|---|---|---|
| IF | female | 21 | 161.0 | 55.8 | 1.59 | 133.7 | Aichi |
| IS | female | 20 | 156.0 | 53.3 | 1.53 | 140.4 | Gifu |
| UF | female | 21 | 156.6 | 48.0 | 1.47 | 125.0 | Aichi |
| KR | female | 21 | 155.2 | 41.8 | 1.38 | 111.8 | Mie |
| SY | female | 21 | 156.5 | 46.0 | 1.44 | 120.0 | Aichi |
| MY | female | 21 | 161.2 | 57.0 | 1.60 | 136.1 | Shizuoka |
| YM | female | 20 | 156.0 | 43.0 | 1.40 | 113.3 | Aichi |
| WS | female | 21 | 159.0 | 52.6 | 1.53 | 130.9 | Aichi |
| IK | female | 21 | 152.3 | 55.0 | 1.59 | 155.7 | Aichi |
| IM | female | 22 | 153.5 | 46.0 | 1.42 | 127.2 | Gifu |
| NE | female | 22 | 157.0 | 53.2 | 1.53 | 137.5 | Gifu |
Table 2: Physical characteristics of subjects.
In accordance with the Declaration of Helsinki, the details of the experiment were sufficiently explained in advance to the subjects, and their voluntary consent was obtained for their participation in the experiment.
The total number of measurements with all eleven subjects, taken at each observation point, was 152. The results on the thermal environment on the date of measurements are shown in Table 3. Depending on whether the observation sites were in the sun or in the shade during the time of the measurement, downward short-wave solar radiation varied widely.
| Date Survey site | Ta [°C] | Tf [°C] | RH [%] | Va [m/s] | RSdwn [W/m2] | RSup [W/m2] | RLdwn [W/m2] | RLup [W/m2] | Weather | |
| 27 Jan. | 1,15 | 4.8- 5.3 | -0.5- 3.6 | 48.4-52.4 | 1.1-3.7 | 60.9- 67.1 | 4.7- 7.8 | 273.4-310.0 | 334.8-349.2 | Fair |
| 31 Jan. | 2,3,4,5,6 | 2.2- 4.5 | -1.3- 3.4 | 50.3-62.4 | 0.6-1.6 | 5.0-149.5 | -14.8- 37.4 | 311.0-331.6 | 340.0-379.6 | Cloudy with occasional snow later occasional fair |
| 1 Feb. | 1,11,12,13,14,15 | 6.0-15.3 | 1.9-21.6 | 29.0-59.4 | 0.6-2.9 | 15.1-497.7 | - 9.9- 64.4 | 207.8-273.7 | 274.7-337.3 | Fair with occasional cloudy |
| 2 Feb. | 1,7,8,9,10,15 | 8.8-11.0 | 6.7-13.3 | 18.6-25.1 | 0.4-2.9 | 67.1-255.8 | 1.4- 44.2 | 305.5-346.7 | 365.4-397.3 | Cloudy with occasionally fair |
| 18 Feb. | 10,11,12,13,14 | 10.3-12.9 | 8.6-21.1 | 35.2-39.6 | 1.2-2.3 | 63.8-711.4 | 3.4-104.0 | 304.0-341.0 | 376.5-411.6 | Fair with occasionally cloudy |
| 21 Feb. | 2,3,4,5,6,7,8,9,10,11,12,13,14 | 10.1-15.7 | 6.2-36.2 | 19.5-36.2 | 0.3-2.3 | 7.4-746.8 | - 9.6-145.4 | 275.3-482.0 | 378.3-450.7 | Clear |
| 23 Feb. | 7,8,9,10,13,14 | 13.5-18.5 | 9.5-25.7 | 22.3-36.5 | 0.9-2.4 | 66.6-688.4 | 14.0-140.7 | 280.9-339.7 | 383.8-457.6 | Fair later slightly cloudy |
| 3 Mar. | 2,3,4,5,6 | 5.1- 7.5 | 1.9-18.8 | 22.8-28.7 | 0.8-6.6 | 30.8-790.0 | - 6.4-143.6 | 294.2-331.7 | 354.0-408.2 | Fair later occasional slightly cloudy |
| 11 Mar, | 2 | 8.3 | 7.5 | 42.5 | 0.6 | 64.3 | 5.9 | 350.1 | 386.6 | Cloudy with occasional fair |
| 14 Mar. | 2,3,4,5,6,7,8,9,10,13,14 | 14.1-21.3 | 1.9-28.5 | 25.3-40.3 | 0.3-1.9 | 87.0-603.6 | 16.0-164.4 | 308.0-368.0 | 383.8-427.9 | Cloudy with occasional fair |
| 17 Mar. | 2,3,4,5,6 | 4.6- 6.9 | 3.8-23.9 | 25.3-32.0 | 0.9-2.1 | 33.4-646.2 | 44.1-128.5 | 296.1-322.3 | 365.9-416.9 | Fair |
| 18 Mar. | 2,3,4,5,6 | 6.5- 8.0 | 4.3-23.1 | 23.5-25.9 | 0.5-2.1 | 72.7-794.0 | 14.4-181.6 | 266.5-319.8 | 364.2-406.3 | Fair later occasional slightly cloudy |
| 22 Mar. | 4 | 16.0 | 25.4 | 41.7 | 2.1 | 733.4 | 49.3 | 335.6 | 420.7 | Cloudy with occasional fair |
| 25 Mar. | 7,8,9,11,12,13,14 | 10.6-13.8 | 11.5-33.4 | 26.6-29.1 | 0.9-2.4 | 88.7-830.9 | 10.8-170.2 | 268.2-343.2 | 386.4-472.0 | Fair later cloudy |
| 28 Mar. | 7,8,9 | 12.0-12.7 | 20.3-38.2 | 9.9-11.4 | 1.1-1.9 | 552.6-933.3 | 44.5-183.1 | 258.0-340.6 | 419.1-461.7 | Clear |
| 29 Mar. | 11,12 | 13.2-13.9 | 11.8-22.3 | 24.9-26.0 | 0.9-1.5 | 329.0-698.1 | 36.3- 82.0 | 221.5-247.8 | 331.2-360.5 | Fair |
| 22 Jul. | 1,7,8,9,10,11,12,13,14,15 | 36.4-41.9 | 34.7-52.5 | 17.5-41.3 | 0.4-1.5 | 16.0-788.7 | -5.4-179.0 | 405.3-462.4 | 446.4-637.3 | Fair |
| 4 Aug. | 1,3,4,6,11,12,13,14 | 28.1-38.6 | 36.9-48.6 | 39.3-60.7 | 0.5-3.0 | 111.8-962.1 | 7.3-154.6 | 460.8-485.9 | 493.7-592.1 | Fair with occasional cloudy |
| 23 Aug. | 1,7,8,9,10,11,12,14,15 | 33.2-42.6 | 31.2-55.1 | 32.0-60.5 | 0.3-1.1 | 44.9-915.4 | -1.6-191.2 | 453.6-501.0 | 495.1-627.0 | Fair with occasional cloudy |
| 26 Aug. | 1,2,3,4,5,11,12,13,14 | 28.0-38.4 | 32.1-56.8 | 34.2-55.2 | 0.5-2.7 | 85.3-887.3 | -1.2-181.9 | 449.8-489.4 | 488.9-608.8 | Fair |
| 1 Sept. | 7,8,9,10,15 | 34.1-36.9 | 31.7-53.3 | 37.3-48.7 | 0.8-1.4 | 306.2-827.6 | 35.8-111.4 | 460.0-489.6 | 525.6-586.5 | Fair with occasional cloudy |
| 6 Sept. | 7,8,9,10,15 | 32.1-36.5 | 31.8-50.0 | 42.2-57.5 | 0.0-1.3 | 71.8-450.4 | 16.1- 62.6 | 452.4-490.9 | 496.5-577.0 | Slightly cloudy with occasional fair |
| 13 Sept. | 4,5,6,7,15 | 24.4-26.0 | 29.6-45.6 | 42.2-51.3 | 0.6-1.3 | 41.1-998.9 | 9.1-302.3 | 444.0-472.0 | 488.9-544.8 | Cloudy with occasional fair |
| 21 Sept. | 2,3,4,5,6,7,11,12,14 | 28.4-33.6 | 28.6-44.9 | 44.0-63.0 | 0.4-1.0 | 72.1-415.0 | 0.8- 80.0 | 420.6-457.1 | 463.9-537.2 | Cloudy |
| 30 Sept. | 6 | 23.4-23.4 | 19.7-19.7 | 58.7-58.7 | 0.9-0.9 | 107.0-107.0 | 12.1- 12.1 | 408.0-408.0 | 422.2-422.2 | Rain with occasional cloudy |
| 7 Oct. | 1,2,3,4,5,6,15 | 25.3-28.5 | 21.8-39.3 | 37.8-45.5 | 0.3-1.1 | 42.1-442.6 | 7.5-106.1 | 393.6-433.7 | 437.4-521.5 | Fair |
| 14 Oct. | 6,7,8,9,10 | 24.4-26.0 | 21.2-34.0 | 42.2-51.3 | 0.3-0.9 | 67.9-229.7 | 7.6- 32.7 | 400.3-436.6 | 451.2-481.9 | Cloudy |
Table 3: Results of field survey.
The influence as a result of leafy shade or the shade of buildings was remarkably apparent in the variation of short-wave solar radiation. Also, the ground surface temperature exceeded 50ºC in the summer and dropped below 0ºC in the winter. Air temperature also had an effect. However, the influence as a result of heating from short-wave solar radiation and radiant cooling from the ground was verified. Although there is a meager contact area between the ground and a standing body, the heat gained by the human body owing to heat conduction was inferred to be influenced strongly by the contacting surface skin temperature.
Relationship between ETFe and mean skin temperature
The changing body system factors were taken as heat transfer area factor (projected area factor, convective heat transfer area factor, radiant heat transfer area factor, conductive heat transfer area factor) and heat transfer coefficient (convective heat transfer coefficient, radiant heat transfer coefficient, resultant heat conductance), effective surface area of clothing, thermal efficiency factor of clothing, thermal efficiency factor of clothing in heat conduction segment, and angle factor of the human body. The values of Miyamoto et al. [35] were used for the projection area ratios of the human body. The values of Kurazumi et al. [1] were used for the convective heat transfer area factor, radiant heat transfer area factor, and conductive heat transfer area factor. The values of Kuwabara et al. [36] were used for the radiant heat transfer coefficient and convective heat transfer coefficient of the human body. The value of Kurazumi et al. [6] was used for the resultant heat conductance. The values of Kurazumi et al. [37] were used for the effective surface area of clothing, owing to the amount of clothing and the thermal efficiency factor of clothing in heat conduction segment [38].
ETFe is an outdoor thermal environment evaluation index, based on the heat balance of the human body. Accordingly, the calculation of the mean skin temperature used for the calculation of the heat balance of the human body was performed using a weighting coefficient that takes into account the convective heat transfer area [39]. Then, the calculation of the mean skin temperature used for the physiological response of the human body was performed, using a weighting coefficient that takes into account heat conduction [40]. The values suggested by Kurazumi et al. [1] were used for the convective heat transfer area factor, the radiant heat transfer area factor, and the conduction heat transfer area factor for the human body. The value suggested by Miyamoto et al. [35] was used for the projection area ratio of the human body. The values suggested by Kuwabara et al. [36] were used for the radiant heat transfer coefficient, and convective heat transfer coefficient of the human body. The value suggested by Hendler et al. [41], found from the reflectance of skin exposed to electromagnetic waves of wavelength 3 μm or more, was used for the emissivity of the human body. The value obtained experimentally by Hendler et al. [41] and Elam et al. [42], found from the reflectance of skin expected to electromagnetic waves of wavelength 3μm or less, was used for the solar radiation absorption coefficient of the human body. The outdoor thermal environment evaluation index ETFe, proposed theoretically by Kurazumi et al. [10], was calculated from weather observation values, the skin temperature of the human body, and clothing insulation.
Figure 3 shows the relation between ETFe and mean skin temperature. If the ETFe for both the simulation from the behavioral thermoregulation model, and the actual value from the subject exposed to an outdoor thermal environment, are high, then the trend is that the mean skin temperature also becomes high. If the ETFe exceeds 40oC, then the increasing trend of mean skin temperature becomes considerably small. This is thought to be because the skin surface controls the temperature increase through the action of cooling, by a sharp increase of water evaporation heat exchange; i.e. sweating. The variation trend of skin temperature as a result of the influence of outdoor thermal environmental conditions is considered to be predictable.
The outdoor thermal environment factors such as short-wave length solar radiation, long-wave thermal radiation and air velocity are the unequal and asymmetric evaluation factors. These evaluation factors might affect the human body even under the conditions in which the entire body heat balance was evened. Those outdoor thermal environment factors such as short-wave length solar radiation and long-wave length thermal radiation, and air velocity can be unequal and asymmetric evaluation factors. The experiment method was selected to measure the effect on human body by making the several subjects stay around the thermal environment measuring equipment. For that reason, even though the thermal environment was same, the subject reaction showed some directivity. Kurazumi et al. [43,44] clarified that there is a part of skin where its skin temperature can easily be affected in unequal and asymmetric thermal radiation environment. In this research left part of the human body skin temperature was measured. The partial skin temperature does not always reflect the condition in which the amount of entire body heat exchange is equaled. In addition, even though the amount of entire body heat exchange is equaled, the effect of shielded heat radiation by such as clothes does not always appear on skin temperature. For that reason, it is normal to have a big dispersion on the result of human reaction experiment carried out in the environment.
High ETFe simulated in summer are relatively low compared to some actual results. The simulated mean skin temperature showed a trend of being around 0.7 ± 0.1(SE)ºC on average lower than the measured values. Low ETFe simulated in winter is relatively high compared to some actual results. The simulated mean skin temperature showed a trend of being around 1.8 ± 0.3(SE)ºC on average higher than the measured values. Also, outdoor environmental conditions, which exhibit comparatively high ETFe as a result of a strong influence of short-wave solar radiation, are higher for the simulated values compared to the actual values.
The amount of heat transfer from short-wave solar radiation is influenced by direct solar radiation absorptance. According to VDI3787-2 [45], the direct solar radiation absorptance of a clothed body is 0.7. However, Watanabe et al. [46] showed that the direct solar radiation absorptance of a body clothed in black is 0.76 and that of a body clothed in white is 0.38. Also, the direct solar radiation absorptance of other clothing combinations or for everyday-clothing falls between the range of direct solar radiation absorptance for a body in black or in white clothing. In this study, a value for the direct solar radiation absorptance of 0.7, standard for a naked body, was used, which is considered to be strongly apparent on the influence of shortwave solar radiation on the body’s heat balance. In addition, there is a difference in the body heat balance and the heat balance of the measuring equipment. In order not to disturb the instrumentation, the subject’s response was evaluated in the vicinity of the instrumentation. Due to the influence of airflow variations or short-wave solar radiation shielding due to shade, exposing the equipment and the subject to the same environment stimulus is extremely difficult. As an observation, this study also took areas affected by shade as measurement points. Short-wave solar radiation formed from the tree density or foliage or micro-climates due to airflow are considered to influence subjects’ responses.
As the behavioral thermoregulation model in this study is an improved Two-Node Model [17,47]. Therefore, this model does not assume that the thermal neutral temperature is much lower than the thermal environment for an indoor environment, the difference with the actual value in a low temperature environment in which the blood vessel contraction coefficient is small, is considered to be large. Also, in a low temperature environment, shivering heat production is assumed to be a steady state expression. However, the measured values are in a varying non-steady state. Thus, the near absence of shivering heat production is considered to be an influence on the prediction’s mean skin temperature. This trend is also shown to be expressed in other thermoregulation models, Tanabe et al. [26]. Thus, as formulas (25) to (30) mentioned, if heat conductance between skin and core layer under neutral condition kn was clarified, heat conductance between skin and core layer kmin is possible to be depend on the ratio of body weight of skin layer α. That is to say, this behavioral thermoregulation model can be adapted for a low temperature environment better.
The simulated and measured values of mean skin temperatures are considered to be in good agreement for the summer in which the air temperature is high and short-wave solar radiation is strong. On the research which compared subject experiment results, carried out in experiment laboratory under fixed thermal environment, and the thermoregulation model, Stolwijk thermoregulation model [19]; 65-node thermoregulation model [26], results, there is about 1 to 1.3ºC difference between [26]. By considering the unfixed outdoor environment condition, the result of this paper can be applicable.
Thus, the difference between the simulated and the actual results, when comparing the mean skin temperature, is thought to be a result of the difference in the heat balance of the equipment and of the human body. However, ETFe based on actual values, and ETFe based on simulated values, are considered to show good agreement.
Looking at the regression lines, an analysis of covariance (ANCOVA) was performed. The statistical analyses were carried out with a significance probability of 0.01. The result revealed that this relationship was parallelism (RMSE=1.68, F(3,209)=1.27, p=0.261). The result revealed that this relationship was homogeneous (Welch’s t-test, RMSE=2.83, t(300)=2.18, p=0.030). It was evident that the simulated data are valid for the mean skin temperature in the outdoor thermal environment.
In this study, the thermoregulation model was developed, which included the thermal influences from short-wave solar radiation and heat conduction. This thermoregulation model was to improve and expand the Gagge’s Two-Node Model [17]. ASHRAE standard 55 [48] is based on the results obtained from Gagge’s Two-Node Model [17]. Therefore, it is applicable to other sex, people, countries, etc. Moreover, the outdoor body heat balance, which was included the outdoor meteorological elements, was theoretically defined by Kurazumi et al. [10]. In addition, the validity of using the outdoor body heat balance that incorporates these environmental factors for an outdoor space was demonstrated by Kurazumi et al. [11,47]. Therefore, it is also applicable to other environmental factors, etc.
For an outdoor space, simulations were made for the thermoregulation response of a human body with changing postures, owing to behavioral thermoregulation, and in order to make the thermal environment of an outdoor space measurable. The Two-Node Model was improved and a thermoregulation model was developed, which included the thermal influences from short-wave solar radiation and heat conduction. The equations of thermal equilibrium of the behavioral thermoregulation model for an outdoor space are shown by being separated into; direct solar radiation segment, which receives solar radiation directly; indirect solar radiation segment, which receives solar radiation through reflection and scattering; and heat conduction segment, which receives heat conduction.
In a cold environment, core temperature is maintained by means of the thermal resistance between core and skin layers, which depends on the variations of the body weight of the skin layer. In contrast, in a hot environment, it is easy to lose the core temperature. The model formula, by ratio of body weight of skin layer of heat conductance between skin and core layer, was included in the new behavioral thermoregulation model.
In order to verify that this thermoregulation model was effective as a simulated model, experiments using subjects were conducted, and the characteristics were clarified. The ETFe based on actual results, and the ETFe based on simulated results, were shown to be in good agreement. The thermoregulation model, which includes the thermal influence from short-wave solar radiation and heat conduction, is shown to be effective when making an outdoor thermal environment evaluation with estimated human body factors; i.e. core temperature; skin temperature; skin wetness.
This model can be applied to the prevention of health hazards, such as heat stroke and thermal environment evaluation. Then, it is possible to develop the bio-weather forecast.