Journal of Stock & Forex Trading
Open Access
ISSN: 2168-9458
ISSN: 2168-9458
Research Article - (2015) Volume 4, Issue 2
Bank default prediction continues to draw attention given the ongoing effects of the recent financial crisis. Seminal works have found that structural models are better predictors of default. In this paper I argue that accounting models predictive ability have been weakened due to the multicollinearity problem and propose principal component analysis to improve the accounting model. The paper then compares accounting and structural default prediction models using a logit analysis and further evaluates the performance of a combination of accounting and structural default models to predict default. The paper uses panel data on US banks from the Federal Deposit Insurance Corporation database between 1995-2012 and the analysis is developed on 519 defaulted bank years and 5,965 non defaulted bank years. The accounting model is improved and outperforms the structural model; the study also finds that a combination of both models performs better than any one model at predicting default in the US banking system.
<The 2008 financial crisis heightened awareness of the management and regulation of the financial sector. The importance of early warning systems (EWS) came into focus as anticipating and identifying any impending crisis was thought to be a better preemptive strike against financial vulnerabilities that could destabilize economies [1,2]. As the crisis heightened the focal point became the banking sector since the crisis originated there. The importance of this sector was not lost on regulators as the Basel Committee on Banking Supervision (July 2011) proposed methodologies to progress the ‘resilience’ of systemically important banks since failure of these institutions had crippling effects on the financial system.
There exists vast literature on the ability to predict financial distress in an institution and it focuses mainly on two types of models, [3-9] all employ either accounting models, structural models or a combination of both to determine default in an institution. While most of the literature has found that structural models are better at detecting default in an institution, Shumway [5] finds that the accounting model is in many cases weakened due to the multicollinearity problem. The idea behind an accounting model being used to assess the financial health of a firm is grounded in the notion that firm’s books can give insight into the health of an institution. Altman [3] employs academics to embrace the use of traditional financial ratios in an attempt to investigate institution failures. Since Altman’s model, which was constructed on a multiple discriminant analysis (MDA) foundation, other accounting models [9,10] using logit and probit analysis have also paved the way for the use of financial ratios in assessing firm health.
On the other hand structural model supporters like Hillegeist et al. [6] find the Merton framework to be more useful in forecasting default as compared to Altman’s accounting framework, their findings have been supported by Reisz and Perlich [7] who also find the Merton framework more useful but conclude that accounting models give more accurate predictions with a shorter time horizon.
Recent works have evaluated the combination of both the structural and accounting models. Such combination models are said to better predict default than any one model. Argarwal and Taffler [11] echo these sentiments; they find that the structural and z score model, applicable to the UK, both possess similar predictive abilities but essentially measure varying aspects of bank distress. Like Argarwal and Taffler [11] other authors Trujillo-Ponce et al., [8] sought to encourage the use of hybrid models that include both structural and accounting information as these are thought to possess even greater predictive abilities than any standalone model. Tinoco and Wilson [12] go a step further and seek not only to combine the accounting and structural frameworks but also include macroeconomic variables in their prediction model.
This paper adds to the exiting literature by (1) employing the unique method of principal component analysis to improve the retention of variable information in the default models. In particular, the transformation process of the variables corrects the multicollinearity problem which plagues the accounting framework. (2) This study encompasses both listed and non-listed banks since it is able to compute structural indicators for all banks in the data set.
In direct contrast to the literature that supports the structural models ability to better detect default, the results of this analysis indicate that the accounting model for banks performs superior in default detection when compared to the structural model. Further to this the combination model which combines both accounting and structural indicators is far superior at detecting default than the accounting model. It stands to reason that the accounting model has been strengthened by the new methodology of applying principal component analysis and has been vastly improved in its ability to predict default.
Following the Introduction, section 2 gives an explanation of the data and methodology employed, section 3 explores the results and finally the paper concludes in section 4.
Data is compiled from the Federal Deposit Insurance Corporation (FDIC) and Bloomberg. The paper uses annual accounting data1 collected from 1995-2012, a total of 6,484 firm years of which 519 are defaulted years.
The default models are developed using a logit framework. The logistic model is a binary response model and can be used to give the probability that an event will occur given the variables said to explain the event. In this case the logit model is used in the analysis of bank failure where Y is a Bernoulli distribution such that:
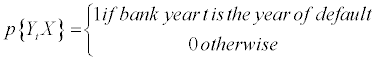 (1)
(1)
The logit model can predict the likelihood of a bank falling into the defaulted category based on the explanatory variables. Following the evaluation of the probability of default (equation 2) and the probability of no default (equation 3) we can then calculate the odds ratio. The odds ratio as seen in (equation 4) is the probability that a bank year is a defaulted year divided by the probability that it is not.
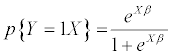 (2)
(2)
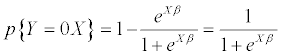 (3)
(3)
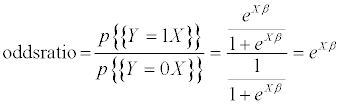 (4)
(4)
If we take the natural logarithm of the odds ratio we get equation 5. While probabilities are restricted to values between 0 and 1 this transformation pins the logit model to values on R. Note that as the probability values near 0 the odds ratio is zero meaning the event coded as default is unlikely to occur, in this instance the logistic model will tend to -∞. Conversely as the probability tends to 1 both the odds ratio and the logistic transformation will tend to +∞.
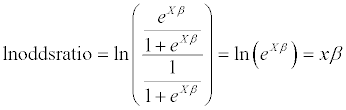 (5)
(5)
As Shumway found most accounting variables tend to be highly correlated and as such the logistic accounting model gave spurious results. In an attempt to make use of the accounting variables and correct for multicollinearity this paper uses the principal component analysis (PCA) methodology. PCA is essentially a variable reduction method used widely in face recognition software. It allows the researcher to reduce the number of variables in the model while retaining most of the information contained in those variables. The components or new variables that result from this exercise can then be used in the econometric analysis.
The literature defines a principal component “as a linear combination of optimally weighted observed variables”. A principal component for n variables is computed as follows:
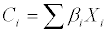 (6)
(6)
Where:
Ci is the principal component
Βi is the coefficient for the variable X1 (given by solving an eigenequation)
Xi is the first explanatory variable
The principal components or the ‘new’ variables have certain characteristics. The first component will explain the majority of the variation in the data and as such will be correlated with the explanatory variables. The second component will explain the variation that was left unexplained by the first component and this too will be correlated with the explanatory variables. Similarly the third component will explain the variation that again was left unexplained by the first two components and this process will carry on until we have n components, with n being equal to the number of explanatory variables, explaining 100 per cent of the variation in the data. More importantly, while the principal components are correlated with the explanatory variables, they are uncorrelated with each other.
Accounting model variables
This section gives the 10 financial ratios in the accounting model which were taken directly from the FDIC database under performance and condition ratios (Table 1). The idea is to utilize publicly available ratios that can give a sense of the financial soundness of the institution as popularized by the CAMEL rating system and the IMF Financial Soundness Indicators (FSI’s).
| Accounting Variable | Expected Sign in Logit Model | Explanation |
|---|---|---|
| Non-Interest Expense to Assets (NIEA) | + | This ratio gives all expenses as a percent of assets. Expenses include salaries, benefits, bonuses, fixed assets, land and building etc. The excessive growth of expenses in relation to assets and gross income is a concern for institutions particularly where bonuses are excessive and can lead to financial strain on a bank. Of course this ratio cannot be analyzed in isolation as expenses may increase due to increased acquisition of land and building and other income generating expenses. |
| Return on Assets (ROA) | - | This ratio is computed as net income after taxes as a percent of assets, it is a profitability ratio and measures an institutions ability to efficiently utilize their assets. |
| Return on Equity (ROE) | - | Like ROA, it is also a profitability indicator but looks at dividing net income before taxes by capital. It gives a measure of the proficiency in the use of an institution’s capital. |
| Loss Allowance to Non-current Loans (LANCL) | - | This ratio is computed by the allowance for losses and leases divided by non-current loans; it measures where losses are accurately being catered for. The expected sign in the logit model is negative; as the ratio falls due to lower allowances or higher non-performing loans there maybe inherent problems as increasing non-current loans usually indicate this. Lower allowances reduce the buffer the bank has to hedge against a deteriorating loan portfolio. As such a lower ratio maybe indicative of higher default probabilities, thus the negative sign. |
| Non-current Assets plus other real estate to assets (NCAORE) | + | This is another ratio used in the logit model, defined as non-current assets which comprise of assets past due 90 days or more or assets placed in accrual status, as a per cent of assets. With the mortgage problems faced by US banks with the sub-prime crisis it is thought that this ratio is significant regarding the sub-prime crisis. A priori we expect the sign to be positive in the logit model, if the ratio increases due to rising noncurrent assets or falling assets, this would indicate some possibility of default thereby increasing the default probability. |
| Non-current Loans to Loans (NCLL) | + | Non-current loans and leases divided by gross loans. This ratio is a measure of the quality of assets in the bank’s portfolio and can be used to identify any possible problems. The expected sign is positive the ratio may increase due to increasing non-performing loans or a shrinking loan portfolio all of which may be indicative of problems. |
| Net Loans and Leases to Core Deposits (NLLCD) | + | Net loans and leases as a percent of core deposits. According to the IMF this ratio can be used in the analysis of liquidity problems in an institution, they explain that an excessively high ratio indicating that deposits are falling, as core depositors unexpectedly withdraw deposits or the bank experiences a run, may speak to liquidity stress in an institution. As such we expect a positive sign in the logit model. |
| Tier1 Risk Based Capital Ratio (T1RBC) | - | This is core capital as a percent of risk- weighted assets. This ratio is based on the Basel Committee on Banking Supervision’s guidelines in capital adequacy measurement. A priori we expect a negative sign with this capital adequacy ratio, as capital increases or risk-weighted assets fall the ratio will increase and the probability of default should decline. |
| Core Capital Leverage Ratio (CCLR) | - | According to the FDIC database this ratio is defined as ‘Tier 1 (core) capital as a percent of average total assets minus ineligible intangibles’ and also acts as a capital adequacy measure, as such we also expect a negative sign a priori. |
| Equity Capital to Assets (ECA), | Computed as equity as a per cent of total assets. This ratio shows what proportion of assets is financed by equity. The benefit of this ratio is that it can be computed as book value or at market value if the company is publicly traded and then gives a bit of market information in the accounting model. This ratio may have to be interpreted in the logit model as it is difficult to pin point a sign a priori. If the numerator is rising the ratio will increase which may lead to a fall in default probabilities. However if the ratio increases due to a declining denominator (total assets) this may be problematic as it may lead to distress on the books and hence increase the probability of default. |
Table 1: Accounting Variables.
Merton model risk indicators
The Merton Model [4] is a framework generally applied to institutions listed on the stock market. Where the volatility of equity, when applied to the Black Scholes option pricing formula, plays a vital role in determining the implied asset values, implied asset volatility, distance to distress and probability of default. In this analysis the banks that are listed on the capital market utilize the general Merton framework to compute the distance to distress, implied asset value and implied asset volatility metrics. However, since most banks in this analysis are not listed on the stock market but are private banks the author engaged an alternative methodology that would allow the inclusion of non-listed banks into the analysis.
Blavy and Souto [3] developed the Merton risk indicators for the Mexican banking system, despite the fact that most banks in Mexico were not listed. They explained that the analysis relied heavily on the volatility of book value assets as opposed to the volatility in market equity as popularized by the Merton framework. They lament that this method does not have the sophistication of incorporating market information but still grants some useful information in the identification of impending default risk to non-listed banks. The method has been successfully employed by Blavy and Souto [13] and Souto, Tabak and Vazquez [11]. To assess the volatility in book value assets, it is felt that declining asset values speak more to default than the alternative, as such the method only accounts for falling assets values, which Blavy and Souto [13] term ‘downside risks’. A priori we would expect the volatility variable to have a positive sign, as asset values become more volatile (downside) the probability of default should rise. The downward volatility of assets is computed as follows below, where σA is the asset volatility and At is the asset value at time t.
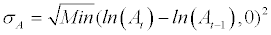 (7)
(7)
We then compute the distance to distress metric as follows; where D is the distress barrier calculated as total deposits plus half of other borrowed funds and other liabilities and r is the 3-month Treasury bill rate. This metric is expected to have a negative sign. As the standard deviations of asset values from the distress barrier become further and further the probability of default is reduced.
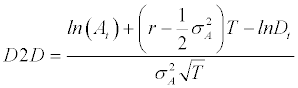 (8)
(8)
The model also includes the asset value variable. In the banks that were listed on the capital market the Merton model allows this to be computed as the implied asset value, which can be thought of as a truer asset value which accounts for the market capitalization. In the alternative methodology popularized by Blavy and Souto [13] there is only the book value of assets and as such the model includes this. The expectation from the asset value variable is simple, the original framework explains that as asset values come close to or fall below the distress barrier the probability of default rises, and as such we expect a negative sign attached to this variable. As asset values fall the general theory will indicate that the probability of default should rise.
In this section we analyze the results from the logit model and apply the principal component analysis framework to assess whether our logistic analysis will improve and assess the ability of the model to accurately predict defaulted versus non-defaulted years. Table 2 gives the results from the accounting logit model, as can be observed most of the signs we expected from our previous discussion have materialized. The logit analysis shows that only 5 of the 10 variables are significant, a closer evaluation reveals that of the 5 significant variables, 3 are significant at α ≤ 10 per cent in the model and even more troubling only 2 variables are significant at α ≤ 5 per cent.
| Variables | Coefficient |
|---|---|
| NIEA | 3.756 |
| ROA | -6.200* |
| ROE | -0.049*** |
| LANCL | -0.056 |
| NCAORE | 2.655 |
| NCLL | 3.265*** |
| NLLCD | 0.004* |
| T1RBC | -3.693 |
| CCLR | -62.702* |
| ECA | 9.590 |
| Cons | -0.089 |
Significant at: * 1 per cent, ** 5 per cent and *** 10 per cent
Table 2: Accounting Logit Model.
Despite the variables having sensible signs we want our variables to explain default of banks and from examination of the raw data it would indicate that these variables do play some significant role in the determination of defaulted years. It would then make sense to analyze the correlation matrix to investigate whether the mere nature of accounting variables being highly correlated is in some way attributing to the problem of insignificant variables.
The correlation matrix (Table 3) confirms the suspicion that many of the accounting model variables by their very nature are highly correlated. In particular the capital adequacy block of variables is highly correlated with each other and with the return on assets, non-current loans to loans and non-current assets and other real estate to assets. While part of the asset quality block appear to be highly correlated with the return on assets. The tendency of these variables to move in tandem may be contributing in part to the majority of variables being deemed insignificant. Most works that have attempted to develop accounting default models of a logistic nature would seek to remove these seemingly insignificant variables from the analysis to retain a more compact model with all variables registering as significant. However the author feels that these variables contribute to the default prediction model and as such engages the principal component analysis to retain the information these variables have.
| NIFA | ROA | ROE | LANCL | NCAORE | NCLL | NLLCD | TIRBC | CCLR | ECA | |
|---|---|---|---|---|---|---|---|---|---|---|
| NIFA | 1 | |||||||||
| ROA | -0.214 | 1 | ||||||||
| ROE | 0.032 | 0.208 | 1 | |||||||
| LANCL | -0.027 | 0.054 | 0.012 | 1 | ||||||
| NCAORE | 0.118 | -0.662 | -0.171 | -0.075 | 1 | |||||
| NCLL | 0.117 | -0.646 | -164 | -0.079 | 0.94 | 1 | ||||
| NLLCD | -0.013 | 0.007 | 0.002 | -0.002 | 0.001 | 0.002 | 1 | |||
| TIRBC | -0.064 | 0.413 | 0.113 | -0.023 | -0.4 | -0.336 | 0.02 | 1 | ||
| CCLR | -0.008 | 0.517 | 0.141 | 0.059 | -0.468 | -0.468 | 0.019 | 0.81 | 1 | |
| ECA | -0.02 | 0.5 | 0.136 | 0.051 | -0.452 | -0.452 | 0.017 | 0.788 | 0.965 | 1 |
Table 3: Correlating Matrix of Accounting Variables.
Following the application of principal component analysis to the accounting variables (Table 4) the first four components explain approximately 74 per cent of the variation in the data and are retained for the logit model seen in Table 5.
| Component | Eigenvalue | Difference | Proportion | Cumulative |
|---|---|---|---|---|
| PC1 | 3.993 | 2.615 | 0.399 | 0.399 |
| PC2 | 1.378 | 0.347 | 0.138 | 0.537 |
| PC3 | 1.031 | 0.032 | 0.103 | 0.640 |
| PC4 | 0.998 | 0.012 | 0.100 | 0.740 |
| PC5 | 0.987 | 0.102 | 0.099 | 0.839 |
| PC6 | 0.885 | 0.492 | 0.089 | 0.927 |
| PC7 | 0.393 | 0.149 | 0.039 | 0.967 |
| PC8 | 0.244 | 0.187 | 0.024 | 0.991 |
| PC9 | 0.057 | 0.024 | 0.006 | 0.997 |
| PC10 | 0.033 | . | 0.003 | 1.000 |
Table 4: Accounting Model Principal Components and Eigenvalues.
Each principal component is correlated to each explanatory variable in the accounting model (Table 6). Correlations in excess of 30 per cent are deemed to be strong. Both PC1 and PC2 explain the capital adequacy block2 of variables as they are positively correlated between 38 per cent and 43 per cent. The positive relationship between the components and the capital adequacy block means that any increase in the capital adequacy variables will lead to an increase in PC1 and PC2.
PC1 and PC2 have a negative sign in the logit model (Table 5) and an increase in PC1 and PC2 therefore means a decline in the probability of default. From this we can see that any increase in the capital adequacy variables therefore leads to a decline in the probability of default and this is in line with a priori expectations since being adequately capitalized is an important aspect in any default analysis.
| Model 1 | Model 2 | |
|---|---|---|
| Cons | -4.529* | -4.521* |
| PC1 | -1.321* | -1.317* |
| PC2 | -0.689* | -0.691* |
| PC4 | 0.215* | 0.202* |
| PC3 | 0.041 |
Note: * 1 per cent
Table 5: Accounting Logit Model with Principal Components.
The signs attached to the non-current portfolio (NCAORE and NCLL) differ for both PC1 and PC2 (Table 6). If we analyze the relationship with PC1 it is quite intuitive as these variables3 increases we expect PC1 to fall and from the logit model (Table 5) we see that the probability of default will increase since PC1 has a negative sign. This is in line with a priori expectations.
| Variable | PC1 | PC2 | PC3 | PC4 |
|---|---|---|---|---|
| NIEA | -0.07 | 0.32 | 0.66 | 0.07 |
| ROA | 0.39 | -0.27 | -0.02 | 0.04 |
| ROE | 0.12 | -0.11 | 0.61 | 0.27 |
| LANCL | 0.05 | -0.10 | -0.14 | -0.49 |
| NCAORE | -0.40 | 0.41 | -0.08 | -0.03 |
| NCLL | -0.39 | 0.44 | -0.09 | -0.03 |
| NLLCD | 0.01 | 0.04 | -0.36 | 0.82 |
| T1RBC | 0.39 | 0.39 | -0.11 | -0.03 |
| CCLR | 0.43 | 0.38 | -0.04 | -0.04 |
| ECA | 0.43 | 0.38 | -0.05 | -0.04 |
Table 6: Relationship between retained Principal Components and Variables.
However, we cannot ignore the strong correlations between these variables and PC2. The positive relationship between NCAORE, NCLL and PC2 may indicate that even though these variables increase it did not adversely affect the default probability (Table 5) since the banks may have been adequately provisioned against any increase in the noncurrent portfolios.
The NIEA variable while strongly related to PC3 (0.66) also has a notable correlation to PC2 (0.32). The sign associated with PC3 and PC2 is positive. Despite initial expectations of a negative relationship, NIEA can increase due to purchase of building; payments made to staff in the form of bonuses which may in turn motivate productivity and so on as such an increase in NIEA due to increasing non-interest expenses may not always adversely affect default. It would be more useful to know if the ratio is increasing due to rising expenses and what type of expenses are driving it. On the other hand, if the ratio increases due in part to falling asset values there may be some cause for concern.
The ROA variable has a strong relationship with PC1 (0.39). Notably the relationship is positive, indicating that an increase in ROA will lead to an increase in the component and from Table 6 any increase in the first component decreases the probability of default, which is as expected. ROE loads on PC3, but this component is subsequently omitted from the logit model due to insignificance.
The merton default model
This section of the paper analyses the results of the Merton structural model, as discussed in the methodology section the focus is placed on three of the financial stability indicators computed by the structural model. The first is the distance to distress (D2D) which gives the number of standard deviations the institution is away from the distress barrier and Sigma, which is the asset volatility variable and finally the implied asset value (book value assets for non-listed banks). As the distance to distress variable gets larger the institution is moving further and further away from the distress barrier and as such we expect a negative sign attached to D2D as seen from Table 5. Conversely the higher the asset volatility (in this case we focus on downside volatility of assets) the more likely is default in the bank and as such the Sigma variable awards a positive sign, the asset value variable also produces a positive sign as expected.
In an attempt to compare like with like and being cognizant that there is little or no loss to the model the author applies the PCA methodology. As seen in Table 7 the first component explains 34 per cent of the data while the second component explains another 33 per cent and the remainder of 32 per cent is explained by the final component.
| Component | Eigenvalue | Difference | Proportion | Cumulative |
|---|---|---|---|---|
| PC1 | 1.029 | 0.031 | 0.343 | 0.343 |
| PC2 | 0.998 | 0.026 | 0.333 | 0.676 |
| PC3 | 0.972 | . | 0.324 | 1.000 |
Table 7:Structural Model Principal Components and Eigenvalues.
Table 6 gives the correlation between the explanatory variables and the components. Given that the assets value variable and the sigma variable load on PC1 and PC3 we conclude that these two components explain the variables in a similar way. This is not surprising since sigma simply captures the downward volatility in asset values based on the [13] methodology for non-listed banks. The distance to distress (D2D) is explained by PC2 with a correlation of 97 per cent.
Asset values have a strong inverse relationship to PC3 (Table 8). From the logit model (Table 9) we observes a positive coefficient for PC3 therefore any fall in PC3 (as a result of rising asset values) will result in a fall in the probability of default this finding is in line with a priori expectations. A contradicting result emerges when we analyze the relationship between the asset value variable and PC1 which has a 69 per cent positive correlation (Table 8). Given that the sign is positive it implies that any increase in asset values will lead to an increase in PC1 and any such increase (Table 9) will cause an increase in default probabilities. This may be attributed to banks erroneously reporting and inflating their asset values pre and during the crisis; as such we may find that many banks who continued to report increasing asset values found themselves defaulted in crisis times.
| Variables | PC1 | PC2 | PC3 |
|---|---|---|---|
| AssetValue | 0.69 | 0.18 | -0.71 |
| D2D | -0.24 | 0.97 | 0.01 |
| Sigma | 0.69 | 0.16 | 0.71 |
Table 8: Relationship between Principal Components and Variables.
While the D2D variable has a high correlation with PC2 (97 per cent) the sign appeared to coincide with intuition as it suggests that any increase in the D2D variable will result in an increase in PC2. From the logit model (Table 7), any increase in PC2 leads to a decrease in the probability of default. However since PC2 is insignificant in the model we analyze D2D in terms of PC1. Table 9 highlights the inverse relationship between D2D and PC1 as D2D rises, PC1 falls and the probability of default also falls. As one would expect, as the institution moves further and further away from the distress barrier the probability of default should decline and as such our findings for D2D stand.
In assessing the volatility of assets we observe a positive relationship between Sigma and PC3, as asset volatility rises so too will PC3 rise and the probability of default will also rise. Asset values also have a strong inverse relationship to PC3. While there is a strong correlation with PC3 (71 per cent), it is also important to observe the relationship with PC1 as the sigma variable is also well explained by this component (69 per cent). PC1 carries the same sign as PC3 and the explanation of the influence of this variable on default remains much the same as above.
Default models evaluation
Predictive ability of models: The final part of the logit analysis, allows us to assess the predictability of the logit model. This section looks at the predictive ability of the accounting model (Table 10). It is important to note that accurate predictions tend to be biased toward the larger data set and since we have a large amount of non-defaulted years, the model correctly predicts 95.74 percent of the non-defaulted years, but only correctly predicts 82.98 per cent of the defaulted years. Notwithstanding this the model correctly classifies the majority of defaulted and non-defaulted years. One limitation, as mentioned above, may be our heavily unbalanced data as we have 5,965 nondefaulted years but only 519 defaulted years.
| Model 1 | Model 2 | |
|---|---|---|
| Cons | -1.097* | -1.070* |
| PC1 | 0.670* | 0.562* |
| PC3 | 0.589* | 0.651* |
| PC2 | -0.672 |
Significant at: * 1 per cent, ** 5 per cent and *** 10 per cent
Table 9:Structural Logit Model with Principal Components.
The predictive ability of the structural model (Table 11) appears weak in comparison to the accounting model predictive power. A minimal 44.42 per cent of the data is correctly classified in the defaulted year’s category of the structural model, compared to 83 per cent correctly classified in the accounting model, barring the question of the applicability of this model. However the author laments that, in an attempt to construct the Merton indicators for non-listed banks much of the data was lost. This may in fact highlight the limited benefits that are gained from attempting to apply a market structure model to banks that are not listed on the capital market.
| Defaulted Years | Non-DefaultedYears | |
|---|---|---|
| percent | ||
| Correctly Classified | 44.42 | 75.04 |
| Incorrectly Classified | 55.58 | 24.96 |
| Total | 100 | 100 |
Table 10:Structural Model Prediction.
Receiver Operating Characteristic (ROC) curve: The ROC curves are used as diagnostic evaluation tools of two binary models. It compares the sensitivity and specificity of both binary classifications. Sensitivity looks at accurately classifying a true positive as positive, in this case as classifying a defaulted year as defaulted and specificity as classifying a true negative as negative in this case, classifying a nondefaulted year as non-defaulted. Essentially it looks at type I versus type II errors in the model. A perfectly predictive model will result in sensitivity and specificity equal to 100 per cent and as such will give coordinates of (0, 1).
The Figure 1 gives the ROC curves for both the accounting and structural model. As is seen by the predictive capability discussion above, the accounting model out performs the structural model in terms of the specificity and sensitivity of the logit models. The curve further from the reference line shows the Accounting Model and it can be observed that the line is closer to the (0,1) coordinate while the Structural Logit Model is much further from these coordinates. The Accounting Model is shown to have an area under the ROC curve as 94 per cent versus a mere 64 per cent from the Structural Model, a sheer sign of the better predictive ability of the accounting analysis.
Combination model
In an attempt to assess whether a combination of both the structural and accounting model will outperform any stand-alone model, the paper combines both and runs the analysis. Adding the Merton structural indicators to the accounting model equation does results in the combination4 model. The logistic method applied to the combination model resulted in many of the explanatory variables being insignificant5 as was seen with the stand-alone accounting model. As such the principal component analysis was applied to the data set and the first four principal components which explain approximately 60 per cent of the variation in the data were retained.
Table 12 gives the relationship between each explanatory variable and the four retained components. The first three variables, NIEA, ROA and ROE all load on the same four components as in the standalone accounting model. The variables NCAORE and NCLL now load on PC1 and PC3 and the capital block of variables load on PC1 only. As regards the structural variables, Asset values and sigma load on PC2 while distance to distress (d2d) loads on PC4. The logit model (Table 13) treats the principal components as explanatory variables as was done previously. PC4 is insignificant in the first logit model and is removed from the analysis. The second logit model shows the first three principal components to be significant. The first principal component has a negative sign attached to the coefficient.
| Defaulted Years | Non-DefaultedYears | |
|---|---|---|
| percent | ||
| Correctly Classified | 44.42 | 75.04 |
| Incorrectly Classified | 55.58 | 24.96 |
| Total | 100 | 100 |
Table 11:Structural Model Prediction.
We can now evaluate ROA as this variable loads on the first component (Table 12). If ROA increases then PC1 will increase, when PC1 increases the probability of default decreases (Table 13). The non-current portfolio (NCAORE and NCLL) also loads on PC1 with a negative sign (Table 12), therefore as these ratios increase PC1 will decrease and then the probability of default increases (Table 13). This is in line with a priori expectations as an increasing non-performing portfolio (barring being adequately provided for) may signal problems for the bank. Similar to our previous analysis it also appears that there is a noteworthy relationship between these variables and PC3, however the relationship is positive and speaks to increasing non-current portfolio decreasing default. As mentioned in the accounting model section this may be due to well provisioned banks that experienced a rising non-current portfolio but were not driven to default. The capital adequacy block of variables (T1RBC, CCLR and ECA) are highly correlated to PC1 and the sign is positive, therefore as these variables increase PC1 will increase and the probability of default will decrease (as seen in the logit model (Table 13)).
| Variable | PC1 | PC2 | PC3 | PC4 |
|---|---|---|---|---|
| NIEA | -0.08 | 0.34 | -0.65 | -0.06 |
| ROA | 0.38 | -0.12 | 0.13 | 0.04 |
| ROE | 0.10 | 0.18 | -0.40 | 0.12 |
| LANCL | 0.06 | -0.07 | -0.11 | -0.09 |
| NCAORE | -0.38 | 0.19 | 0.32 | -0.02 |
| NCLL | -0.36 | 0.20 | 0.34 | -0.04 |
| NLLCD | 0.02 | 0.04 | 0.14 | -0.10 |
| T1RBC | 0.41 | 0.14 | 0.13 | -0.06 |
| CCLR | 0.44 | 0.21 | 0.12 | -0.04 |
| ECA | 0.43 | 0.22 | 0.13 | -0.04 |
| AssetValue | 0.04 | 0.51 | 0.30 | 0.21 |
| D2D | 0.01 | -0.11 | -0.01 | 0.95 |
| Sigma | -0.10 | 0.61 | -0.10 | 0.07 |
Table 12: Relationship between Combination Model Variables and Principal Components.
| Model1 | Model2 | |
|---|---|---|
| Cons | -2.41* | -2.41* |
| PC1 | -1.56* | -1.56* |
| PC2 | -0.63* | -0.63* |
| PC3 | -0.29* | -0.29* |
| PC4 | -0.04 |
Significant at: * 1 per cent, ** 5 per cent and *** 10 per cent
Table 13: Combination Logit Model with Principal Components.
The structural variables (asset value and sigma) appear to load on PC2 with a positive sign, indicating that any increase in asset values and volatility will increase PC2 and will thereby decrease the probability of default since PC2 carries a negative sign in the logit model. While the result is sound for the asset value variable, one would expect that any increase in downward volatility should increase default probabilities, however, the question of accurate reporting of asset values and the volatility in the assets again comes into question.
The variables NIEA and ROE both load on PC3 with negative signs meaning any increase in these variables result in a decrease in PC3 (Table 12) and results in an increase in the probability of default. Rising non-interest expenses to assets (NIEA) maybe indicative of problems where these expenditures are on bonuses and other activities that do not enhance the bank’s ability to conduct its main business and is therefore in line with a priori expectations. However any increase in the returns on equity of a firm should be indicative of increased profitability of the bank and is thought to decrease the probability of default. However, in many instances the equity component on the balance is usually treated as a residual and may in fact contribute little knowledge of the distress the bank is experiencing on the capital market.
The last component PC4 is highly correlated with d2d, the distance to distress variable. Despite the correlation being 95 per cent, this component was omitted from the logistic analysis since it was found to be insignificant. It then means that the distance to distress metric only plays a minimal role in the logistic analysis as it is weakly correlated to the variables LANCL and NLLCD seem weakly correlated with all the principal components that were retained.
Predictive ability of combination model: An evaluation of the predictive ability of the combination model uncovers some notable results. It appears that the predictive ability of the combination model out performs that of any stand-alone model. The combination model accurately classifies 90.78 per cent of defaulted banks as defaulted (Table 14) whereas the accounting model only managed to accurately classify 82.98 per cent of defaulted banks as defaulted (Table 10) and contrasted with the substandard classification of a mere 44.42 per cent for the structural model (Table 11). However in terms of accurately classifying non-defaulted bank years as non-defaulted the accounting model (95.74 per cent) outperforms both the structural model (75.04 per cent) and combination model (81.70 per cent). It is important to note that all the classification models used a cutoff point of 25 per cent.
| Defaulted Years | Non-Defaulted Years | |
|---|---|---|
| percent | ||
| Correctly Classified | 90.78 | 81.70 |
| Incorrectly Classified | 9.22 | 18.30 |
| Total | 100 | 100 |
Table 14:Combination Model Prediction.
While some works support the use of structural models in default prediction due to their forward looking ability and the inclusion of market information, this paper has found the structural analysis to be less useful when compared to the accounting analysis for all banks (listed and non-listed). The paper also finds that the combination of accounting and structural model variables is better at determining default of banks than any stand-alone model. The paper uses PCA to ensure the retention of as much information in the accounting model and is also applied to the structural data without any loss to the analysis. In improving the monitoring of the financial system regulators should seek to analyze both accounting and structural model variables as the shortcomings of any one model is minimized when assessing the combination model. The debate surrounding the best prediction model (accounting versus structural models) is nullified if emphasis is placed on a combination of these models. It appears from this work and other works that the marriage of these frameworks will shed greater light on the default risks banks face.
1While the paper uses annual data it was thought that utilizing the most recent bank accounts would aid in the prediction of any constructed model, as such the author includes the last available data for all defaulted institutions. Some defaulted banks had first, second or third quarter balance sheet data available just prior to default and this was included in the model since it gave information on the bank just before default.
3Due to increasing non-current assets and other real estate or decreasing assets (NCAORE) or rising non-current loans and falling loans (NCLL)
4DIi, t = NIEAi,t +ROAi,t +ROEi,t +LANCLi,t +NCAOREi,t +NCLLi,t +NLLCDi,t +T 1RBCi,t +CCLRi,t + ECAi,t + Asset Valuei,t + D2Di,t + Sigmai,t Where DI is the default indicator for bank i at time period t and can take a value of 0 (no default) or 1 (default).