Journal of Geology & Geophysics
Open Access
ISSN: 2381-8719
ISSN: 2381-8719
Research Article - (2013) Volume 2, Issue 2
A crucial part of pre-stack reverse time migration is forward numerical computation of seismic wave propagation. However, there exist serious spurious reflections from truncated model edges during the simulation of wave propagation. In this work, we present a novel absorbing boundary layer named nearly perfectly matched layer (NPML) to suppress artificial reflections from model boundaries. Different from seismic numerical study on first-order partial differential equations, NPML with second-order acoustic equations is implemented here. Through checking snapshots of seismic wave propagation and seismograms, the numerical modeling results illustrate that the NPML is able to effectively absorb the outgoing waves at the truncated domain. Finally, our NPML algorithms are combined with the implementation of pre-stack reverse time migration to achieve accurate depth image of subsurface.
Keywords: Nearly perfectly matched layer, Second-order acoustic equations, Numerical modeling
Pre-stack reverse time migration, which can provide us best depth image of complex geological structures compared with other migration techniques [1-3], has been used as an routine step in seismic data processing due to rapid growth and application of supercomputing techniques (e.g. parallel computing and graphics processing Unit) in recent years [4,5]. An important part of pre-stack reverse time migration is the seismic numerical simulation of wave propagation. To simulate wave propagation, the computational domain has to be truncated surrounding the model boundaries due to finite computational ability of computers. This kind of truncation causes serious spurious reflections which come from the truncated model boundaries [6,7]. To suppress those unwanted spurious reflections, many absorbing boundary conditions and absorbing layers have been introduced in the last several decades [8-11]. Cummer [12] first proposed nearly perfectly matched layer (NPML) to absorb outgoing waves in electromagnetic media. Subsequently, some authors applied NPML technique to acoustic and elastic media [13,14]. The NPML demonstrates significant absorbing performance through comparing with other PMLs [15,16]. In addition, the NPML has many advantages over other absorbing layers in that it uses fewer auxiliary variables and fewer differential equations and it does not alter the original governing equations in linear media [13,14]. However, all above mentioned NPML frameworks were related to first-order differential equations. Regarding the issue that the classical wave equations are second-order linear partial differential equations, McGarry and Moghaddom [17] derived the second-order wave equations with NPML boundary condition. However, detailed and further study is needed to explore the absorbing ability of the NPML in second-order wave equations. In addition, finite difference operators [18,19] are used for both second-order derivatives in the spatial domain and time domain. This paper is comprised of the following parts. First, the second-order two-dimensional acoustic equations with NPML boundary condition are introduced. Second, a homogeneous model is used for checking the absorbing efficiency of the NPML through comparing snapshots of seismic wave propagation and seismograms with reference model. Finally, NPML algorithms are inserted into pre-stack reverse time migration to reconstruct image of a five-layer model. Modeling test results show that NPML has a significant absorbing ability to suppress the artificial reflections from model boundaries and can be an alternative choice of absorbing boundary conditions.
Acoustic wave equations
For homogenous media, the 2D second-order acoustic equations can be described in the time domain as [20,21,17]
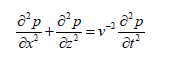 (1)
(1)
The above equation can be also written by the form of partial derivatives using subscripts
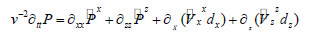 (2)
(2)
where P(x, z,t) is the acoustic pressure field (N/m2 = Pa) and v(x, z) is the acoustic velocity (m/s); t, x and z are time, horizontal and vertical coordinates, respectively.
NPML implementation
After a series of deduction in [17], the final 2Dsecond-order acoustic wave equations with nearly perfectly matched layer (NPML) are formulated by
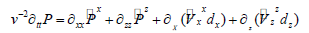 (3)
(3)
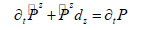 (4)
(4)
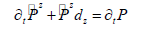 (5)
(5)
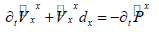 (6)
(6)
and
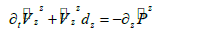 (7)
(7)
where 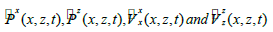 are auxiliary variables, dx and dz are damping coefficients along x and z coordinate directions. dx is expressed as
are auxiliary variables, dx and dz are damping coefficients along x and z coordinate directions. dx is expressed as 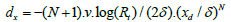 [22], where N is a constant (choose 2 in this study) that controls the decay rate, Rt is the theoretical reflection coefficient which is within the range of 10-2 to 10-6, ∂ is the thickness of the NPML layer, xd is the horizontal distances from grid to the inner boundary within the NPML absorbing layer. Through looking at equations (2) and (3), we can tell that wave equation with NPML holds the similar structure of the original governing equation.
[22], where N is a constant (choose 2 in this study) that controls the decay rate, Rt is the theoretical reflection coefficient which is within the range of 10-2 to 10-6, ∂ is the thickness of the NPML layer, xd is the horizontal distances from grid to the inner boundary within the NPML absorbing layer. Through looking at equations (2) and (3), we can tell that wave equation with NPML holds the similar structure of the original governing equation.
Finite difference method for the discrete NPML model
Centered-finite difference approximations [18,19] are applied to second-order time derivatives and first-order spatial derivatives in equations (3)-(7), whereas forward-finite difference approximations are used in first-order time derivatives. The detailed description of finite difference implementation can be written
as follows:
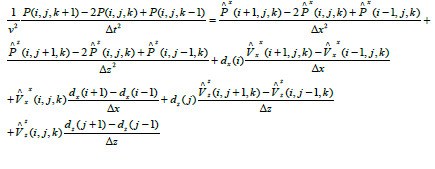 (8)
(8)
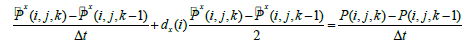 (9)
(9)
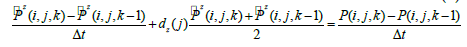 (10)
(10)
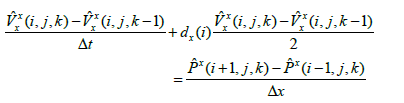 (11)
(11)
and
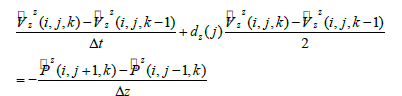 (12)
(12)
where i and j are indexes in position along x and z coordinates, whereas k is an time index; Δx, Δz and Δt are respectively grid interval and time step.
Comparison between second-order and first-order NPML equations
In comparison with seven first-order acoustic NPML equations derived by [13], we only need total five in the implementation of seismic modeling deduced from classical second-order acoustic equation. In addition, there are more variables in first-order NPML equations than those used in second-order NPML equations. That may lead to more memory requirements in seismic modeling with first-order NPML equations.
Seismic numerical simulation of wave propagation in a 2D homogeneous acoustic model (named model-1) is used to check the efficiency of the NPML based on second-order acoustic wave equations. The length and width of the acoustic model (Figure 1) are 8000 m and 3000 m. The model has a velocity of 3000 m/s. The grid space and time sampling of numerical simulation by finite difference are selected respectively 10 m and 1 ms. The time sampling obeys the Courant-Friedrichs-Lewy stability condition [23]. The exploration point source S is located at the grid (100, 275), which is a Ricker wavelet of a 15 Hz dominant frequency with t0=0.08 s shift. We take 20 grids as the width of each NPML layer. The simulation is run 4000 time steps for a total duration of 4 s. The real number 0.001 is selected as the theoretical reflection coefficient during the implementation of the NPML. Figure 2 shows snapshots of the pressure field of seismic wave propagation at 0.2 s, 0.8 s, 1.6 s and 2.4 s without the application of NPML to the model. One can observe the presence of strong artificial reflections from the edges of the model. Figure 3 illustrates snapshots of the pressure field of seismic wave propagation at 0.2 s, 0.8 s, 1.6s and 2.4 s with the application of NPML to the model. These results show that the NPML has a significant absorbing performance by thoroughly attenuating artificial reflections. To further verify the absorbing capability of the NPML, the seismic signals recorded by a receiver R at the grid (775, 25) in the model-1 (Figure 1) are compared with these from the same source-receiver geometry in reference model (Figure 4). The receiver R in Figure 1 is placed close to the inner boundaries of NPML layers. It will be very easy for us to observe distinct artificial reflections if NPML layers do not work well. Figure 4 is a 2D reference model with size 20000×15000 m that is assumed to be an unbounded model (Earth). The source S and the receiver R are placed at grids (500, 1000) and (1175, 750), respectively. Thus, we have the same sourcereceiver configurations between both model-1 and reference model. We also set up the reference model with the same parameters of source, grid space, time sampling and NPML width as we do for the model-1. Figure 5 shows the seismograms of pressure field at receivers for both models. The dashed black line and solid gray line indicate respectively the seismograms recorded at receivers of model-1 and reference model. The agreement between the two seismograms is fairly satisfactory. That means absorbing ability of the NPML is significant.
The depth image of pre-stack reverse time migration
A 2D five-layer model with size 8000×6000 m is used in this numerical experiment (Figure 6). The velocities from the top down of the model are 3000 m/s, 3400 m/s, 4000 m/s, 4300 m/s, 5000 m/s. The same modeling parameters used in model-1 are applied in this study, such as time step, grid space, and source and NPML coefficients. This model includes dipping and graben structures which are typical geologic features. Figures 7 and 8 show the snapshots of pressure field of the acoustic wave propagation (0.2 s, 0.8 s, 1.8 s and 2.6 s) and shot gather using NPML layers from source grid (25, 25), respectively (Figure 8). We can come to a conclusion that the NPML suppresses unwanted reflection waves successfully and has excellent absorbing efficiency. To implement reverse time migration, 188 shots with 40 m of shot space are collected along the surface. The cross-correlation imaging condition is applied to pre-stack reverse time migration shot by shot [24,25]. Figure 9 is the final migration image after stacking prestack reverse time migration results from all shots. One can observe that the final migration result (Figure 9) matches the real model (Figure 6) very well.
The nearly perfectly matched layer (NPML) was applied to the 2D second-order acoustic equations for attenuating the outgoing waves at the truncated model boundaries. From the observation of snapshots of seismic wave propagation, the seismograms at a receiver far from the source, and depth image by pre-stack reverse time migration, we can reach a conclusion that the NPML has a significant absorbing performance. Given the success of model experiences, NPML algorithms will be further applied to seismic wave propagation and imaging in various types of media.
Gulsah Metin and Can Ozsoy would like to thank the Turkish Petroleum Corporation (TPAO) for its financial support. The authors appreciate Drs. Edip Baysal and Orhan Yilmaz for their help in migration at Paradigm. We also thank Drs. Kumar Ramachandran and Bryan Tapp for their helpful suggestions. The Fortran codes related to parameter assignments of perfectly matched layer and source were provided from Dr. Dimitri Komatitsch. Velocity models were generated by programs from CREWES at University of Calgary. The authors also thank to an anonymous reviewer for helpful comments and suggestions.