Photopolymerization has been widely used in applications ranging from chemical engineering to biomedical and biomaterials [1-4]. It has been used for production of catheters, hearing aids, surgical masks, medical filters, and blood analysis sensors [2]. Photopolymers have also been explored for uses in dentistry, drug delivery, tissue engineering and cell encapsulation systems [3]. Both ultraviolet, visible and infrared lights (360 to 1000 nm) have been used as the photoinitiators for various photosensitizers [3,4].

For ophthalmology applications, corneal collagen cross linking (CXL) systems have been commercialized for years for human clinical uses [5-10]. Photochemical kinetics of CXL and the biomechanical properties of corneal tissue after CXL are reported [11,12]. However, much less efforts have been invested in basic theoretical studies of photopolymerization [13-21], where Lin presented the first dynamic modeling for the safety of CXL [17-18]. CXL has been used clinically for various corneal deceases such as corneal keratoconus, corneal keratitis, corneal ectasia, corneal ulcers, and thin corneas prior to LASIK vision corrections [5]. Other potential applications include the reduction of postoperation regress in vision corrections and scleral treatment in malign myopia, scleromalacia and low tension glaucoma [5].

The safety and efficacy issues of CXL have been explored clinically and theoretically [10,19-27]. To increase the speed of CXL procedures, accelerated CXL using high UV power (9 to 45 mW/cm²) [28-32]. In addition, pulsed mode of the UV light was proposed for potential improvement on CXL efficacy [33-35] as well as femtosecond-laserassisted pocket was proposed [36]. More recently, a corneal topography-guided CXL was commercialized by Avedro based on a pending US patent [37]. The safety of CXL would be significantly improved if the epithelium could be left in situ . Several methods have been reported for this purpose including the use of benzalkonium chloride EDTA, gentamicin, iontophoresis, as well as minimal trauma (through epithelial poke marks) to the epithelium [10]. A sufficient concentration of riboflavin is prerequired and can be achieved by several methods [5]: (1) diffusion in the de-epithelialized stroma (standard method); (2) diffusion through the epithelium into the stroma (transepithelial method); or (3) direct introduction of riboflavin into the stroma (pocket technique, ring technique, needle technique); (4) enrichment of riboflavin in the stroma by iontophoresis [38].

In CXL, both type-I and type-II photochemical reactions occur [11]. Type-I mechanism is favored at low oxygen concentrations, and type- II mechanism is favored at high oxygen concentrations. In type-I mechanism, the substrate reacts with the sensitizer excited state to generate radicals or radical ions, respectively, by hydrogen atoms or electron transfer. In type-II mechanism, the excited sensitizer reacts with oxygen to form singlet molecular oxygen. The singlet molecular oxygen then acts on tissue to produce additional cross-linked bonds [11].

It has been reported that oxygen concentration in the cornea is modulated by UV irradiance and temperature and quickly decreases at the beginning of UV light exposure [11]. The oxygen concentration tends to deplete within about 10-15 seconds for irradiance of 3 mW/cm² and within about 3-5 seconds for irradiance of 30 mW/ cm²[11]. By using pulsed UV light of a specific duty cycle, frequency, and irradiance, input from both Type I and Type II photochemical kinetic mechanisms may be optimized to achieve the greatest amount of photochemical efficiency. The rate of reactions may either be increased or decreased by regulating one of the parameters such as the irradiance, the dose, the on/off duty cycle, riboflavin concentration, soak time, and others [11,34,37].

The critical issues of CXL to be explored in this paper are characterized by the following ten (10) key parameters: the 3 extinction coefficients (Aj, with j=1,2,3), concentration (C) and diffusion depth (D) of riboflavin, UV light dose (E), corneal thickness (z), and finally the cytotoxic energy threshold of endothelial cells (Ed). The dose is further defined by the product of the light intensity (I) and the exposure duration (t), i.e., E=It. The extinction coefficients (Aj with j=1, 2, 3) are further defined by three absorption constants of the UV light in riboflavin (without corneal stroma), in the photolysis product, and in the corneal stroma (without riboflavin).

This study will demonstrate that the conventionally accepted criterion having a safety dose E*=5.4 J/cm² and a corneal thickness z*>400 μm is just one of the special case meeting our condition (1) above-stated. Without specifying the parameters (Aj,C,Ed,D), the fixed parameter set of (E*,z*) = (5.4 J/cm², 400 μm) as the safety condition is meaningless. For examples, a dose of 5.4 J/cm² might still damage the endothelial cells even for thick cornea (>450 μm). On the other hand, a thin cornea (<350 μm) may be still safe even under a high dose (>6.0 J/cm²) under a safety set of (Aj,C,D), for example, having C>2.0% and D>300 μm. Furthermore, the safety dose E* is proportional to the cytotoxic threshold of endothelial cells (Ed). Therefore, accurate safety dose (E*) relies upon accurate (Ed) which is not available for human cornea and was estimated (or proposed) to be 0.65 J/cm² by prior work based on the measured animal data [11]. For example, the conventional E*=5.4 J/cm² would be adjusted 20% higher or lower, when Ed could be accurately measured (in human cornea) and showing a 20% deviating from the estimated value of 0.65 J/cm². Similarly, the conventional cornea safety thickness z*>400 μm also requires adjustment to a range of (350-450) μm.

Moreover, the conventionally accepted UV light absorption in RF solution is based only on it initial (at t=0) intensity and ignoring the RF dynamic depletion causing the steady-state intensity higher than the initial value. Therefore, it underestimates the dynamic light intensity or overestimate the safety dose. Greater details will be shown in this study.

Optimizing of the treatment parameters to reach a sufficient biomechanical effect in the cornea and the safety, to avoid damage of the endothelium, lens or retina. Many investigations were necessary for the fine-tuning of these treatment parameters. Post CXL stiffness increase showing the optimal features and my theory predicts that 5.4 J/cm² dose might be twice overdone and 2.7 J/cm² could be more effective. On the other hand the accelerated CXL based on the linear theory of Bunsen Roscoe law to shorten the irradiation time is undervalued. For example, 30 mW/cm² power should need about 4 to 5 minutes rather than the conventionally believed 3 minutes based on a dose of 5.4 J/cm² dose.

To the best of my knowledge, this paper presents the first in-depth analysis of corneal cross linking via analytic formulas which is derived in the Appendix. The critical issues explored in this paper including the safety dose (E*), the cross linking time (T*) and the efficacy defined by the increase of corneal stiffness (S) which are characterized by nine parameters: the three extinction coefficients, concentration and diffusion depth of the riboflavin solution, the UV light dose, irradiation duration, the cytotoxic energy threshold of endothelial cells and the corneal thickness. This study demonstrates that the linear theory of Bunsen Roscoe law requires a nonlinear revision which shows optimal UV dose and concentration for maximum stiffness increasing. The safety and efficacy of CXL are actually two competing factors. Higher dose (given by longer exposure time and/or larger intensity of the UV light) suffers higher risk, however, it can also achieve higher depletion (or efficacy) of the riboflavin (RF). The RF depletion level may be used to define the CXL crosslinking time (T*) given by when the RF concentration (at a given corneal depth, z) is depleted to exp(-M) of its initial value. This study will demonstrate that the linear theory based Bunsen Roscoe law [21] to shorten the irradiation time requires a nonlinear revision.

Numerical calculations for the dynamic profile of RF concentration and the UV light intensity are presented to validate our analytic formulas (see Appendix). Our theory will show that the safety dose (E*) and the corneal safe thickness (z*) cannot be set as a constant. Instead, they are variable functions defined by the combined parameter set (A,C,Ed,D). Finally, we will present various safety zones, defined by (C*,D*), as the guidance for feature clinical studies. This study will use the currently available (or measured) data for A1, A3 and Ed, whereas the unknown parameters A2 and D will be treated as free parameters within the clinically recognized ranges.

This paper will focus on the comprehensive analysis based on analytic formulas and provide new concepts relating to the above clinically important issues, whereas full analysis based on numerical simulation will be presented elsewhere.

The modeling system

As shown in Figure 1, a corneal model consists of its epithelial layer and the underlying stroma collagen. The UV light is normal incident to the corneal surface. A typical CXL protocol is to administer RF (approximately 0.1% to 0.25%) on the corneal surface 5 to 10 times at 2 to 5 minute intervals and wait until the RF solution diffuses into the top layer at approximately 200 to 300 μm. The CXL procedures could be conducted (as shown by Figure 1) either with epithelium removed (epi-off) with a 0.1% riboflavin-dextran solution or with epithelium intact (epi-on) with a 0.25% riboflavin aqueous solution. It was known that riboflavin diffusion depth in the epi-on case is normally less than that of epi-off and therefore the epi-on is less efficient [5].

Figure 1: A corneal model system under UV light crosslinking for the epi-on (A) and epi-off (B) case, where z is along the corneal thickness direction (z=0 for the corneal surface); the red dotted curves define the riboflavin diffusion boundaries.

The epi-on case having two layers of different medium (the epithelium and the stroma) is more complicated than the epi-off case. The theory developed in this study can apply to both cases by slight revisions. However, we will focus on the more efficient epi-off case as shown by Figure 2, where the stroma having an initial concentration C₀ and non-uniform RF diffusion in the stroma defined by C₀(z) = C₀0 F(z,D), having a diffusion depth (D).

Figure 2: The initial (at t=0 before the UV light exposure) RF concentration distribution inside the stroma collagen given by a distribution function F(z,D), having a diffusion depth (D).

In the above described eye model, the UV light intensity in the corneal stroma is given by a revised time-dependent Lambert-Beer law [19,20]

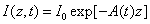(1)

Where the time-dependent extinction coefficient A(t) shows the dynamic feature of the UV light absorption due to the RF concentration depletion. Without the RF, A(t) becomes a constant given by the absorption coefficient of the corneal stroma tissue reported to be [26]A=2.3Q, with Q= (1/cm). With the RF in the stroma, the initial (at t=0) overall absorption has an extra absorption defined by the extinction coefficient and initial concentration of the RF, i.e., A (t=0) =2.3 (Q +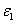C₀), with the reported data [27]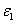= 204 (%·cm)^-1. For t>0, A(t) is an increasing function due to the deletion of C₀ in time and defined by both the extinction coefficient of the RF(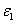) and its photolysis product (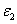) which is not yet available for human, but was estimated to be about 80 to 120 (%·cm)^-1, based on measured data in RF solution under UV light irradiation [20].

In the following, we will focus on the results and discussion of the clinical issues, whereas the details of the mathematical derivation of related formulas, Eq. (A1) to (A9), are shown in the Appendix.

In general, UV light dynamic intensity in the corneal stroma is given by the integration of Eq. (A1.b) (see Appendix)

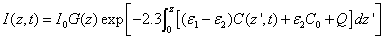(2.a)

With the time-dependent RF concentration given by, from Eq (A3),

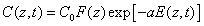(2.b)

Where we have introduced the initial RF distribution (as shown by Figure 1) by F(z) =1-0.5z/D having a penetration depth (D). Schumacher et al. [21] reported a simplified model assuming a timeindependent C(z,t) without depletion, or a=0 in Eq. (2.b). Which lead to the overestimated RF absorption in Eq. (2.a). Despite their initial distribution of F(z,D), the dynamic profile of C(z,t) was totally ignored in their simple model.

UV light dynamic intensity

The initial UV light intensity (at t=0) is given by, Eq. (A5.b), 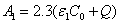, 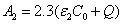with m=1.0. For =204(%·cm)^-1, =102 (%·cm)^-1 and Q=13.9 cm^-1 it becomes

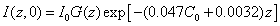(3.a)

where z in μm and �0 in %; and the steady light intensity

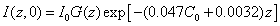(3.b)

For example, for the uniform case with G(z)=1, for C₀= 0.1%, we obtain = (0.45, 0.2, 0.09, 0.04) I₀, and �(�, ∞)= (0.57, 0.32, 0.19, 0.1) I₀, at z = (100, 200, 300, 400) μm, respectively. For a corneal thickness of z = 400 μm, the intensity at that depth increases from its initial value 4% I₀ to the steady state value 10% I₀ for the case of C₀ = 0.1%, which reduce to 0.6% I₀ and 4% I₀, respectively, for a higher C₀ = 0.2%. For C₀ = 0.1%, at z = 400 μm, the calculated data of Spoerl et al. [23] 18% I₀ was over estimated comparing to 4% I₀ (initially) and 10% I₀ (steady-state) of this study. The error of Spoerl resulted from the assumption of 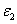=Q = 0 in Eq. (2) and will also overestimate the safety dose.

Safety aspects

The cytotoxic UV light intensity threshold (I*) of the endothelial cells reported by Wollensak et al. [25], I*= 0.35 mW/cm² and limits the maximum light intensity to 0.35/0.18=1.94 mW/cm², based on Spoerl et al. [23], which is much lower than the currently used value ranging from 9 to 45 mW/cm². In comparison, the safety light intensity calculated in this study, based on Eq. (3), is 0.35/0.04=8.5 mW/cm² (initially) and 0.35/0.1=3.5 mW/cm² at steady-state, which are much higher and closer to the clinically used data. However, the safety criteria should not be governed only by the light intensity. Safety dose (or energy) should be better criteria.

The safety dose E*= tI₀ is defined by the cytotoxic energy threshold of endothelial cells (Ed), i.e., E* is the maximum allowed total energy absorbed by the endothelial cells at a depth (z). From Eq. (A7) of the Appendix, it is given by an analytic formula

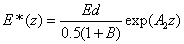(4)

with 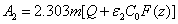and the fit parameter m= (0.8-0.9) depending on the values of 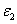= (80-40).

The cytotoxic energy threshold was reported by Wollensak et al. [23,25] in rabbits as Ed= 0.65 (J/cm²), calculated by 0.36 (mW/cm²) × 60 × 30=0.65 (J/cm²). They also reported the dose safety of E*= 5.4 J/cm² as the standard protocol based on the estimated animal data of 3.0 (mW/cm²) × 60 × 3= 5.4 (J/cm²) without knowing the human data.

The analytic formula, Eq. (3), shows that the safety dose E* (z,t) is a nonlinear function of various parameters besides the cytotoxic energy threshold. Therefore the conventionally criteria believed by researchers in the past years having a safety dose of 5.4 (J/cm²) dose and a minimum corneal thickness of 400 um, based on an animal cytotoxic energy threshold Ed= 0.65 (J/cm²), would require further justification when the human data is available.

The following calculations are based on the parameters of 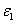=204 (%.cm) 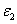=102 (%.cm) and Q=13.9 (cm^-1), where 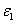and Q are measured human data, whereas the extinction coefficient of the photolysis product (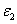) is not yet available in human cornea which is chosen to be half of 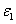, or 102 (%.cm)^-1 . We will also use the cytotoxic energy threshold of endothelial cells, Ed=0.65 (J/cm ) reported by Wollensak et al. [25].

As shown in Figure 3, the safety dose (E*) is an increasing function of the corneal thickness (z). For examples, E*= (1.9, 2.3, 3.7) J/cm², for z= (350, 400, 450) μm, for D=200 μm and C₀=0.1%, which increases to E*= (4.3, 4.5, 9.0) J/cm², for a higher C₀=0.2%. That is, higher concentration (C₀) allows higher dose (E*= tI₀), or higher light intensity (I₀) for a given exposure duration (t), or a longer exposure duration for a given I₀.

Figure 3: The safety dose (E*) versus C₀ for corneal thickness z= (350, 400, 450) μm (curves 1,2 3), for D=200 μm (left figure), and 400 μm (right figure), where the red line represents E*=5.4 J/cm2.

For a fixed corneal thickness of z=400 μm and (i) D=200 μm, the safety conditions are: E*= (2.3, 4.5) J/cm² for C₀= (0.1, 0.2) %; and (ii) D=400 μm, E*= (3.1, 8.2) J/cm². For a deep diffusion of D=400 μm E*= (2.0, 3.1, 4.5) J/cm² (for C₀= 0.1%), and E*= (4.3, 8.0, 14) J/cm² (for C₀= 0.2%), are allowed for corneal thickness of z= (350, 400, 450) μm. Figure 3 also shows that the safety dose (E*) is an increasing function of the concentration (C₀) and the diffusion depth (D) for a given corneal thickness of 400 μm. For C₀= 0.1%, E*= (2.3, 3.1) J/cm² for D= (200, 400) μm, which increases to E*= (4.5, 8.2) J/cm² for a higher C₀= 0.2%.

Based on Figure 3, we found that the commonly used dose 5.4 J/cm² will meet our safety criterion under the following conditions (given by the crossing points of the red lines): (i) for a deep diffusion with D=400 μm, corneal thickness z>350 μm for C₀=0.185%; z>400 μm, for C=0.15%; and z>450 μm for C₀=0.125%; (ii) for shallow diffusion with D=200 μm, one requires higher concentrations z>350 μm for C₀=0.27%; z>400 μm, for C₀=0.23%; z>450 μm for C₀=0.2%. For a corneal thickness of 400 μm, one requires C>0.23% for D = 200 μm or C>0.15% for D=400 μm (Figure 4).

Figure 4: The normalized safety dose (E*/E_d) for corneal thickness z=(350, 400, 450) μm (curves 1,2 3) for D=300 μm, where the red line represents E*/E_d=5.4/0.65= 8.3.

Figure 5 shows the safety zone, based on a safety dose 5.4 (J/cm²) for corneal thickness of 350 μm and 400 μm, indicating that thicker corneas offer a larger safety zones. Figure 5 shows that the commonly used dose of 5.4 J/cm² and 400 μm corneal thickness is outside the safety zone, unless C₀ >0.11% and D>400 μm. These calculated data are based on cytotoxic energy threshold of endothelial cells, E_d=0.65 (J/cm²), reported by Wollensak et al. [25] for rabbits. When C₀=0.1% is used, the commonly used dose 5.4 (J/cm²) is not safe unless the cornea is thicker than 500 μm and D = 400 μm.

Figure 5: The safety zone (indicated by the un-shaded areas) for corneal thickness of 350 μm (left) and 400 μm (right).

For C =0.1% with z=400 μm and D=300 μm and a range of Ed = (0.5-0.85) (J/cm ), the calculated safety dose E* = (3.5-6.8) (J/cm ), if =102 (%.cm) is chosen. For a range of 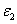= (80-140) (%.cm) the calculated safet dose E*= (4.5-5.0) and (6.0-9.0) (J/cm ), for C =0.1% and 0.2%, respectively, with Ed = 0.65(J/cm ). Therefore without knowing the actual human data of Ed and 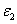, the safety dose should be in the range of (3.5-6.5) (J/cm ) for C = 0.1% with D=300 μm ; and inreases to the range of (4.5-12) (J/cm ) for C = 0.2%. The conventionally believed safety dose 5.4 (J/cm ) based on rabbit data of Ed = 0.65 (J/cm ), may be off by 15% to 40% to be known by future accurate measurement of Ed and in human.The general safety feature of CXL, as shown by Eq. (4), is characterized by the combined effects of the seven parameters: the extinction coefficients (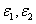), RF initial concentration (C ) and its diffusion depth (D), the UV light intensity (I₀) and dose (E=I₀t), irradiation duration (t), and the corneal thickness (z). For a given damage threshold (Ed) of the endothelium, the safety of CXL is governed by the parameter set (E*, 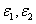, D, z, C ). The basic features of safety issues are summarized as follows: larger value of the product(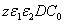), as shown by Eq. (4), allows higher light safety dose (E*= tI ), or a longer irradiation time (for a given light intensity), or a higher intensity (for a given irradiation duration);for a given corneal thickness (z), higher light dose requires a larger or product of (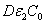) i.e., deeper diffusion depth (D) or higher concentration, or higher photolysis product absorption (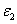) is required to protect the endothelium;

• for a given corneal thickness (z) and light dose, a small diffusion (D) requires a high concentration, and vice versa;

• for a given light safety dose (E*), a thin cornea (or small z) requires a high concentration (C₀), or a large diffusion depth (D).

The cross linking time (T*)

From Eq. (A6) of Appendix, an analytic formula for the normalized cross linking time is given by

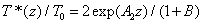(5)

Where the surface cross linking time (at z=0), T₀=161(M/I₀), with T₀ in seconds, I₀ in mW/cm², for quantum yield assumed to be =0.1. For M=2 (or a concentration depletion level of 13.5% of its initial value), T₀ = (32, 10.7) seconds, for I₀ = (10, 30) mW/cm².

As shown by Figure 6, based on Eq. (5), that T*(z) is a nonlinear increasing function of z, C and the diffusion depth (D), whereas it is a decreasing function of the product of the light intensity and extinction coefficient. For examples, for z=400 μm, T*= (9.9, 19.5, 13.3, 37.5)T , for the case of (D, C ) = (200 μm, 0.1%), (200 μm, 0.2%), (400 μm, 0.1%), and (400 μm, 0.2%), respectively. For a UV light having an intensity 30 mW/cm , it will take 10.7 seconds (T ) to deplete the surface concentration, and take (106, 208, 142, 401) seconds, respectively, for the above 4 cases. Above calculated values are based on the choice of M=2 and a quantum yield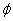=0.1. For higher quantum yield of 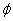=0.2, T*(z) will be reduced to half, due to the reduction of T₀. The quantum yield of CXL in human cornea is not yet available.

Figure 6: The normalized cross linking time (T*/T0) versus C₀ for a corneal thickness z=400 μm based on Eq. (12), for D= (200, 400, 1000) μm, shown by curves 1,2,3, respectively.

The CXL efficacy and stiffness

The safety and efficacy of CXL are actually two competing factors. Higher dose (given by longer exposure time and/or larger intensity of the UV light) suffers higher risk, however, it can also achieve higher depletion (or efficacy) of the riboflavin (RF). The RF depletion level may be used to define the CXL crosslinking time (T*) given by when the RF concentration (at a given corneal depth, z) is depleted to exp(- M) of its initial value.

The efficacy of CXL is defined by the increase of the corneal collagen stiffness (S) after UV light exposure, given by Eq. (A9) of the Appendix. The normalized stiffness, S(z,t)/K0, is shown in Figure 7 calculated numerically based on the coupled kinetic equations for C₀ = (0.1, 0.2, 0.3) % and a cross linking depth z=300 μm with diffusion depth D=300 μm, and UV exposure time t=100 seconds. Figure 7 shows that the stiffness profile has an optimal UV light dose (E0) ranging from 1.0 to 2.0 (J/cm²), particularly for low concentration cases. When the light dose is too high, the stiffness increase is reduced because of the stronger depletion of C₀ due to higher dose. The optimal condition may be calculated by taking dS/dE0= 0.

Figure 7: The increase in normalized stiffness (S/K0) versus UV light dose (E0) at various RF initial concentration C₀ = (0.1, 0.2, 0.3) % (for curve 1, 2, 3) for cross linking depth z=300 μm and D=300 μm.

Figure 8 shows S/K0 versus RF initial concentration (C₀) at various UV light intensity I₀ = 3, 10, 30 mW/cm² (for curve 1, 2, 3). These data show that there is a complex competing effects between the UV light intensity and the RF concentration causing the crossing curves. For example, the high intensity (curves 2 with I₀ = 20 mW/cm²) has lower S than the low intensity curves 1 (with I₀ =3 mW/cm²) and curves 2 (with I₀ =10 mW/cm²), for the regime of C₀ < 0.15%.

The optimal feature of the efficacy of CXL defined by the increase of the corneal collagen stiffness (S) was reported in animal models [21,28-29]. It was also reported in a modeling system of Schumacher et al. [21] which, however, was based on a simplified linear modeling. Comparing Figure 4 of Schumacher et al. [21] and Figures 7 and 8 of this study, one may see that Where the surface cross linking time (at z=0), T₀=161(M/I₀), with T₀ in seconds, I₀ in mW/cm², for quantum yield assumed to be =0.1. For M=2 (or a concentration depletion level of 13.5% of its initial value), T₀ = (32, 10.7) seconds, for I₀ = (10, 30) mW/cm².

Figure 8: Normalized stiffness S/K0 versus RF initial concentration (C₀) at various UV light intensity I₀ = 3, 10, 30 mW/cm2 (for curve 1,2,3), for a cross linking depth z=300 μm, t=200 seconds, and D=300 μm.

A comprehensive model shows that the kinetics of UV lightphotoinitiated corneal cross linking is characterized by the key parameters of: the extinction coefficients, concentration and the diffusion depth of the riboflavin, the UV light intensity, dose, irradiation duration and the corneal thickness. Optimal UV light dose and concentration for maximum stiffness increase is resulted from the competing between the light dose and the RF concentration depletion.

The safety dose (E*), shown by Eq. (4), depends on the parameter set (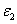, C , Ed, D, z) and has a wide range of 3.5 to 12 (J/cm ) for RF concentration C = (0.1%-0.2%), diffusion depth D= (200-400) μm, 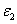= (80-140) (%·cm) and Ed = (0.45-0.85) (J/cm ). The cross linking time, Eq. (5), T* is shown to be inverse proportional to the UV light intensity. Higher light intensity and smaller initiator concentration require a shorter T* to achieve a given cross linking depth. Based on our nonlinear theory for the stiffness increase, the conventionally proposed UV light dose 5.4 J/cm should be reduced to the optimal values (shown by Figure 7) of 1.0 to 2.0 J/cm depending on the RF concentration. This study has used the free parameters of the extinction coefficient of the photolysis product (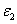) and the quantum yield of CXL which would require further measurements in human to justify its accuracy.

Figure 9: The calculated safety dose (E*) versus z for C₀=(0.1, 0.2, 0.25)%, for curves for curves (1,2,3), where the dotted curves are the exact numerical data and the solid curves are the fit Eq. (A7) and (A5.d) with m=0.85.

Figure 10: Same as Figure 7, but for C₀ = 0.1% (left figure) and 0.2% (right figure) for D= (300, 400, 1000 μm).

This work was supported by the internal grant of New Vision Inc, and also partially supported by a grant from Talent-Xiamen (XM-200) program (Xiamen Science & Technology Bureau, China).

Derivation of the analytic formulas

Kinetic equations

For a polymerization system illuminated by a UV light, the concentration of the unreacted photoinitiator 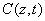And the UV light intensity 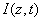may be described by [1,2,7,8]

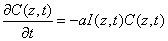(A1)

and

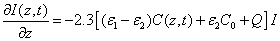(A2)

where 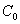is the initial value, 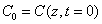; and 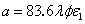, with 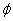being the quantum yield, λ being the light wavelength 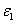and and 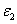being the molar extinction coefficient of the initiator and the photolysis product, respectively; Q is the absorption coefficient of the monomer and the polymer repeat unit. In our calculations, the following units are used: 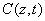in mM, 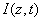in (mW/cm²), λ in cm, Q in cm^-1 and 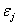(with j=1,2) in (mM·cm)^-1. For the general case with non-uniform photoinitiator concentration given by a distribution function F(z), or 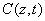=C F(z),, and when 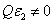, the more realistic case that the photolysis product partially absorbs the UV light, the coupled differential Eqs. (1) and (2) have been only numerical solved so far [7-10]. In this study, for the first time, analytic formulas for the general case of non-uniform system without the assumption of Q=0 or 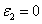are presented as follows. Cross linking time

We will first derive analytic formulas for the cross linking time (T*) which is defined by the time needed to deplete the photoinitiator concentration, or completion of the cross linking under a UV light illustration.

The time integration of Eq. (A1) over time (t) leads to

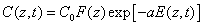(A3.a)

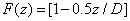(A3.b)

Where E (z,t) is the dose (or energy) of the UV light absorbed by the cornea for an irradiation time (t) at depth (z), given by

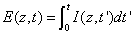(A3.c)

Where we have assumed an initial non-uniform photoinitiator concentration given by a distribution function F(z), with D being the distribution depth and the flat distribution or uniform case is given by when D>> 1.0 mm for a corneal thickness of 350 to 550 μm.

The integration of Eq. (A2) over z leads to

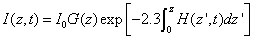(A4.a)

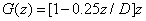(A4.b)

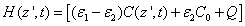(A4.c)

Schumacher et al. [21] has reported a simplified model assuming a constant C(z,t) without including its time-dependent depletion. Their formulas also ignored the absorption from the photolysis product. Therefore they have overestimated the RF absorption. Despite their initial distribution of C₀(z), the dynamic profile of C(z,t) was totally ignored in their simple model.

A comprehensive method, in the linear regime of time, Eq.(A3.c) may be well approximated by the time integration of the mean value of the initial (I₁) and steady-state (I₂) intensity, which are given by the integration of Eq, (A4.c) for C(z,t=0)=C₀F(z) and C(z,t>>500 seconds)=0, respectively. We obtain the following analytic formulas for the UV dose

E(z,t) = 0.5(tI2)(1+B), (A5.a)

where I1 and I2 are given by (for j=1,2)

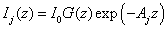(A5.b)

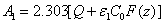(A5.c)

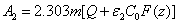(A5.d)

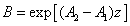(A5.e)

In Eq. (A5.d), m is a free parameter (having a range of 0.8 to 1.0) to be fit numerically later. We note that G (z) in Eq. (A4.c) is resulted from the integration of F(z) over z. Using G(z). Above described technique, presented for the first time, based on a lot of investigation on the numerical results. Validation of Eq. (A5) with a fit parameter, m, to be shown later.

Cross linking time (T*) has not been well defined in prior works. We have chosen to define T* by one of our most preferred definition based on the level of photoinitiator concentration depletion as follows. T* is defined by 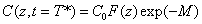, where M defines the degree of the photo initiator concentration depletion. From Eq. (A3.a), we find M=aE. Let t=T* in Eq. (A5.a), we obtain an analytic formula for the cross linking time w here the surface cross linking time (at z=0) is given by

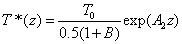(A6)

where the surface cross linking time (at z=0) is given by 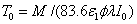which is inverse proportional to the UV light initial intensity and its absorption by the photoinitiator. However, it is linearly proportional to the value of M chosen. For examples, M =1 and 2 represent, respectively, a concentration depletion level 0.367 and 0.135 of its initial value. In this study, we will choose M=2 to make sure the initiator is over 85% depleted. However, the normalized cross linking time, T*/T₀, is independent to the choice of M. Therefore our data based on T*/T₀ universally provides the guidance without specifying the M value.

The safety dose

The safety dose E*= tI₀ is given by when the UV light dose E (z,t) equals to the cytotoxic energy threshold [25] of endothelial cells (Ed) at depth (z), or when E (z,t)=Ed. From Eq. (5.a) and solve for E*=tI₀, we obtain an analytic formula for the safety dose

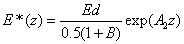(A7)

The CXL efficacy and stiffness

The kinetic equation of the rate of polymerization is mainly determined by the rate of reacting monomers given by [1,11,21]

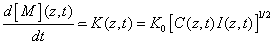(A8)

where the rate function K(z,t) is proportional to the square root of the photoinitiation rate defined in Eq. (17). Therefore our previously defined cross linking time (T*) giving the degree of the RF concentration depletion also defines the depletion rate of the monomer concentration, that is the efficacy of the polymerization of the monomer, or the cross linking process.

The efficacy of CXL is further defined by the increase in corneal stiffness (S) after CXL defined by [11] S = 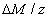, where 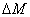is the total amount of induced cross-links obtained by integrating Eq.(8) over time and space.

Therefore

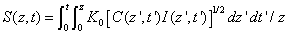(A9)

Validation of the analytic formulas

As shown in Figure 9 and 10, the exact numerical data and the fit Eq. (A7) and (A5.d) with m=0.85 for various concentration and diffusion depth (D) for Q=102 (1/cm). The other best fit values are m=0.9 for Q=140 (1/cm) and m=0.8, for Q=80(1/cm).