Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2014) Volume 4, Issue 2
A minimal wheelbase length of a four-wheeled walker was analyzed for prevention of tipping on slopes surfaces by a theoretical analysis of a two-dimensional mechanical model in a sagittal plane. The minimal wheelbase length was obtained from the lower limit of the safety condition derived from the mechanical model. It depended on some design and environmental factors. The normal force applied at the handgrip and the acceleration of walker movement were human factors for ergonomic design of the four-wheeled walker. They were measured by force transducers and acceleration sensors with the use of a commercial walker for validation of the mechanical model. The subjects were ten aged males and ten aged females. The minimal wheelbase length was lengthened with a weaker normal force applied at the handgrip during uphill movement. However, it was shortened during downhill movement. Female subjects should use a walker with a longer wheelbase because they produced a weaker normal force at the handgrip than male subjects. The walker accelerated more and decelerated more on the downhill, but a longer wheelbase was not obtained by a larger acceleration during steeper downhill movement. The higher handgrip led to a longer wheelbase obviously, and the mass of the walker was not a critical design factor. The minimal wheelbase length should be longer on a high friction road, but it was not easy for users to handle the walker. The minimal wheelbase length was shorter than the actual wheelbase length of the commercial walkers. Many commercial walkers were designed that their handgrip was positioned near the rear wheels. This arrangement was a valid design from an ergonomic point of view because it maintained a margin of walker stability for prevention of tipping.
A four-wheeled walker is an assistive device used to support body posture and to prevent injuries from falling incurred by elderly persons during normal gait. In general, it is composed of metal frames with four wheels and a handgrip. It is mainly used outdoors by comparatively healthy elderly persons. The four-wheeled walker has the principal function of gait assistance but also serves other purposes, e.g., as a baggage carrier or as a seat for rest [1,2]. The walker could also assist elderly users with partial weight-bearing gait [3,4]. Similar to a walking frame, the base of support is widened by the walker [5,6]. Thus, elderly users are able to walk with more stable posture with the walker.
Finkel et al. [1] investigated the safety of the four-wheeled walker in terms of its function as a seat for rest. The seat and the center of gravity should be placed closer to the braked wheels of the walker. Such a design would transmit a larger normal force through the braked wheels. However, safety should be considered from the principal function of gait assistance. The benefits of using a four-wheeled walker have not been examined in certain situations, especially on sloped surfaces. From the viewpoint of gait assistance, miniaturization is one direction for the enhancement of the usefulness of the four-wheeled walker because a miniaturized walker would provide users high mobility and controllability. There are three dimensions for miniaturization: a length, a width, and a height of the walker. Optimized wheelbase length between the front and rear wheels is a design factor to be considered for a miniaturized walker. The tread between the left and right wheels is not a design factor because it is regulated by the environment in which the four-wheeled walker is used. Hall et al. [7] described, for a walking frame, that a wide-based frame was stable but this advantage would be offset by the difficulty of maneuvering the frame within the confined space. The height of the four-wheeled walker is regulated by the handgrip position. Commercial four-wheeled walkers in Japan have a handgrip height from 0.72 m to 1.00 m [8], although the handgrip is adjustable to a preferred height for various users with different physical characteristics and different aims of usage [2]. A walker without wheels was recommended in which the top of the walker was aligned with the ulnar styloid when the user stood beside the frame with arms held loosely in a relaxed position [9].
Thus, the wheelbase length is the most important factor for a walker’s miniaturization among the various ergonomic viewpoints in terms of its design. However, a shorter wheelbase lessens the stability of the four-wheeled walker and also enhances the user’s risk of falling. The walker is easily tipped by any disturbance if the wheelbase was much shorter. The relation between the wheelbase length and the stability of the four-wheeled walker should be examined more closely. In addition, sloped surfaces exist in outdoor walking environments. Usage and safety of the four-wheeled walker vary depending on the slope angle of the walking environment because the tangential component of the gravitational force is applied backward during uphill movement and forward during downhill movement. For usage of the four-wheeled walker, Takanokura [2] suggested that movement on a low-friction downhill compelled distinct effort from users compared with movement on a flat or an uphill surface. The user is required to maintain an erect trunk with a higher handgrip and to press on the handgrip strongly in the perpendicular direction. However, the safety of the four-wheeled walker on sloped surfaces has not been investigated.
The specific question of this study was how far we could shorten the wheelbase of the walker during normal gait on sloped surfaces. We developed a two-dimensional mechanical model of the four-wheeled walker in a sagittal plane and established a safety condition in which users could use the walker without tipping while walking normally on a sloped surface. The minimal wheelbase length was obtained from the lower limit of the safety condition for prevention of tipping. It depended on some design and environmental factors. Since the normal force applied at the handgrip and the acceleration of walker movement had been unknown human factors in actual usage, they were measured by using a commercial walker to give validity to the model analysis of the walker. We discussed which factor was critical for determination of the minimal wheelbase length by analyzing the mechanical model.
Development of mechanical model for four-wheeled walker
Figure 1 illustrates forces applied to a walker during an acceleration phase on a slope with an angle φ in a sagittal plane. A user walked with the walker in an upper right-hand direction by pushing on a handgrip. The walker had a mass mw, a handgrip height H, and a wheelbase length L. The gravitational force mwg and the inertial force mwa were applied to the center of mass of the walker, where g and a were the acceleration of gravity and walker movement, respectively. The one-dimensional translational acceleration a was applied to the walker because the walker moved along the slope and was not rotated during normal walking. The gravitational force was perpendicular to the horizontal surface, but the inertial force was parallel to the slope. The handgrip was placed on a tangential length lh from front wheels. The walker had a center of mass. Its location was defined as the tangential and normal length, lct and lcn, from front wheels to the walker center of mass. Ground reaction forces were applied at four wheels. At the front wheels, the ground reaction force was divided into the tangential component Rfwt and the normal component Rfwn. At the rear wheels, it was composed of the tangential component Rrwt and the normal component Rrwn.
The pushing force applied at the handgrip by the user was divided into a tangential component Fht and a normal component Fhn to the sloped surfaces. The tangential force Fht was equal to the sum of the friction between the road and wheels, the inertial force mwa, and the tangential component of the gravitational force mwg. We could obtain
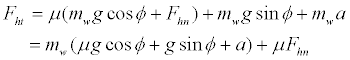 (1)
(1)
where μ was a friction coefficient.
At the front wheels, the moment of the pushing force applied at the handgrip was balanced with the moments induced by the gravitational force mwg and the inertial force mwa at the center of mass as well as by the normal component of the ground reaction force at the rear wheels Rrwn. The equilibrium of the moment around the front wheels was obtained as
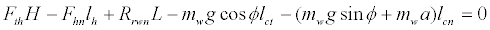 (2)
(2)
Putting equation (1) into equation (2), Rrwn was estimated as
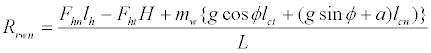
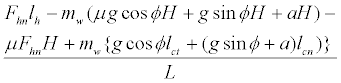
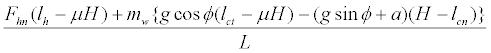 (3)
(3)
If Rrwn<0, the walker was upended because the rear wheels were lifted. Furthermore, we could obtain the equilibrium of the moment around the rear wheels:
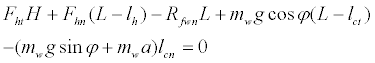 (4)
(4)
Putting equation (1) into equation (4), we could derive:

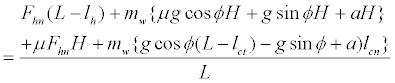
 (5)
(5)
If Rfwn<0, the front wheels would be lifted, and the walker would be upended.
From equations (3) and (5), a stable condition of the walker was expressed as an inequality in terms of its tangential length from the handgrip to the front wheels lh. We obtained the inequality from equation (3) with Rrwn≥0:
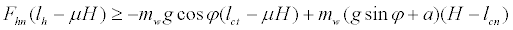 (6)
(6)
The inequality for lh was expressed as follows:
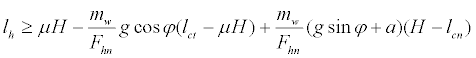 (7)
(7)
We also derived the inequality from equation (5) with Rfwn≥0:
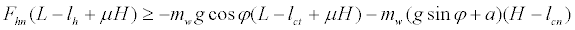 (8)
(8)
The inequality for lh was expressed as follows:
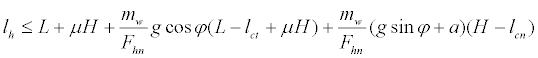 (9)
(9)
We could obtain the stable condition by incorporating equation (7) with equation (9):
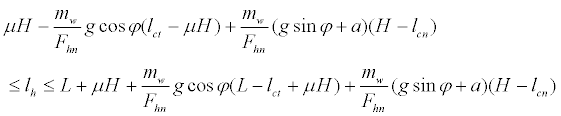 (10)
(10)
The stable condition was safe during normal gait, but not safe when the user was stopped. If the handgrip was placed farther back than the location of the rear wheels, the stopped user would lose balance when he or she pushed the handgrip downward. The walker was safe if the handgrip was placed in the area surrounded by the four wheels, i.e., at the base support of the walker.
The length from the front wheels to the center of mass, lct and lcn, was expressed by linear functions of the wheelbase length L or the handgrip height H: lct=ctL or lcn=cnH. The scale parameters were 0≤ct≤1 or 0≤cn≤1. Thus, a safety condition for prevention of tipping was obtained as
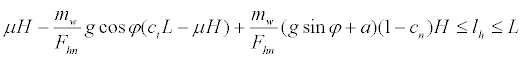 (11)
(11)
This condition indicated that the user could use the walker without tipping during normal gait, even at the lower limit of equation (11). Thus, we could obtain the minimal wheelbase length Lmin for prevention of tipping by arranging the handgrip just above the rear wheels (lh = Lmin):
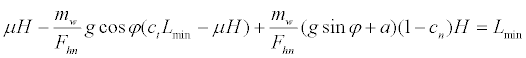 (12)
(12)
Equation (12) was transformed as
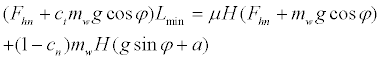 (13)
(13)
As a result, the minimal wheelbase length Lmin was derived as
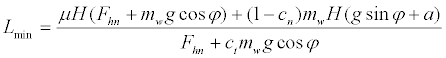 (14)
(14)
As shown in equation (14), Lmin varied nonlinearly with the normal force applied at the handgrip Fhn, the mass of walker mw, and the slope angle φ. However, it was lengthened linearly with the friction coefficient μ, the handgrip height H, and the acceleration a. In this model, the human factors were Fhn and a. The design factors were mw and H. The environmental factors were μ and φ.
Measurement of human factors: Normal Force Fhn and Acceleration a
As shown in equation (14), the minimal wheelbase length Lmin for prevention of tipping depended on the normal force applied at the handgrip Fhn and the acceleration of walker movement a. The relation between Lmin and these variables will be investigated theoretically in the next section; however, the normal force Fhn and the acceleration a had not been measured yet during actual usage of the walker.
Therefore, we measured them by using two force transducers (CLS-100NA, Tokyo Sokki Kenkyujo, Japan) and two acceleration sensors (ARF-20A, Tokyo Sokki Kenkyujo, Japan), respectively, with a commercial walker (Carry-Suruhn Hi, Maki Lifetech, Japan) as shown in Figure 2. The force transducers were placed on the longitudinal frames. The custom-made handgrip was put on the force transducers. The normal force applied at the handgrip Fhn was the sum of the measured forces by the force transducers on the left and right longitudinal frames. The handgrip implemented the force transducers could be set at three kinds of height H: 0.82 m, 0.92 m, and 1.02 m. The acceleration sensors were placed on a plastic plate fixed to the transverse frame with use of adhesive tapes. They detected the tangential and the normal accelerations of the walker movement, respectively. We confirmed that the tangential acceleration was larger than the normal one because the walker was moved parallel to the slope. Therefore, we used only the tangential acceleration for further analysis.
The measured signals were recorded on a compact flash card into a dynamic strain recorder (DC-204R, Tokyo Sokki Kenkyujo, Japan), which was placed onto the chair of the walker, with the sampling rate of 100 Hz. The acceleration sensor signal was only filtered by a lowpass filter implemented in the dynamic strain recorder with the cutoff frequency at 30 Hz. The recorded data were moved to a personal computer, and they were filtered again by the FIR digital low-pass filter with a hamming window. The cut-off frequency was 4.0 Hz. The order of the filter coefficient was 101.
The subjects were ten aged males (age: 60-74 years; height: 166.3 ± 5.6 cm; weight: 62.0 ± 4.9 kg) and ten aged females (age: 60-70 years; height: 155.8 ± 3.7 cm; weight: 51.7 ± 5.6 kg). They did not have any gait disorder and were able to walk without assistive devices such as a cane. The experimental procedures of this study were approved by the ethics committee of Kanagawa University. Informed consent of the subjects was obtained before participation of the experiment. This experiment was performed on an asphalt road approximately 10 m long at the following slope angle φ: a flat road of 0 degrees, a gentle uphill and downhill course of 5 degrees, and a steep uphill and downhill course of 10 degrees. The subject walked twice with the walker under the same condition. As a result, the number of trials was 30 times (5 slope angles × 3 handgrip heights × 2 trials) for each subject. First, the experimenter held the walker, and the subject did not grasp the handgrip. By the instruction of the experimenter, the subject grasped the handgrip and started to move forward with the walker. At the end of the road, the subject stopped walking and released his or her hands from the handgrip, and then the experimenter held the walker.
Since the measured normal force Fhn and acceleration a would fluctuate during the gait phase, we extracted the maximum values of the measured Fhn and a. The measured data would also depend on gender, the subject, the slope angle φ and the handgrip height H. Gender and the subject were factors between subjects. The others were factors within each subject. Hence, we used a split-plot factorial design analysis of variance (ANOVA) for the maximal Fhn and maximal a [10]. The factors included gender (male, female) × the slope angle φ (steep downhill, gentle downhill, flat, gentle uphill, steep uphill) × the handgrip height H (low, middle, high). We performed the Tukey’s post-hoc analysis if the main effect of a factor or an interaction between factors was significant. The significance level was set as P<0.01.
First, we analyzed the relations between the minimal wheelbase length Lmin and other variables of the theoretical model. The handgrip height, H, the friction coefficient, μ, and the location of the center of mass, ct and cn, were not considered because higher H and μ led to a longer wheelbase obviously as shown in equation (14) and Figure 1. Consideration of ct and cn was not easy to recognize the theoretical results and discuss its effect on walker design. It was out of scope of this study.
Figure 3 shows the theoretical prediction of the relation between Lmin and the normal force at the handgrip Fhn by varying the slope angle φ from -10 to 10 degrees during steady walking of a=0.0 m/s2. We varied Fhn from 0 N to 200 N because the maximal Fhn ranged from 19 N to 163 N as described lately in measured data of human factors. Commercial walkers in Japan had a mass mw from 2.9 kg to 10.6 kg [8]. Most users preferred a lighter walker; therefore, we used three kinds of mw: 1.0 kg, 5.0 kg, and 10.0 kg. They corresponded to the lighter, the middle, and the heavier walkers. The friction coefficient μ was determined as 0.13 for the asphalt road [2]. The handgrip was set at a higher position as H=1.0 m. We assumed the center of mass as ct=0.5 and cn=0.5, indicating that it was positioned at half length of the wheelbase and half height of the handgrip. The theoretical prediction indicated that Lmin was lengthened with a weaker Fhn during uphill or flat road movement, but it was shortened during downhill movement. It was also lengthened with the heavier mw especially during uphill movement. Regardless of mw, the shortest length of Lmin was 0.08 m at Fhn=0.0 N and φ=-10.0 degrees, and the longest length of Lmin was 0.44 m at Fhn=0.0 N and φ=10.0 degrees.
Figure 3: Minimal wheelbase length Lmin on asphalt road (μ=0.13) with varied normal force at handgrip Fhn and slope angle ϕ. Handgrip height H was 1.0 m. Mass of the walker mw was (a) 1.0 kg, (b) 5.0 kg, and (c) 10.0 kg. (b) Normal force applied at handgrip Fhn was 90N. (c) Normal force applied at handgrip Fhn was 160N. *hn should be subscript
Figure 4 shows the relation between the minimal wheelbase length Lmin and the mass of the walker mw with varying φ during steady walking. The mass mw varied continuously from 0.0 kg to 10.0 kg. We used three kinds of Fhn: 20 N, 90 N, and 160 N. The friction coefficient, the handgrip height, and the center of mass were the same as those used previously: μ =0.13, H=1.0 m, ct=0.5, and cn=0.5. The theoretical prediction indicated that, during steeper uphill movement, Lmin was lengthened with the heavier mw, especially at the weaker Fhn. If the normal force Fhn was 20 N as shown in Figure 4(a), Lmin was lengthened to 0.35 m with the heavier mw during steeper uphill movement, but it was around 0.10 m during steeper downhill movement. The shortest length of Lmin was 0.10 m at mw=10.0 kg and φ=-10.0 degrees, and the longest length of Lmin was 0.35 m at mw=10.0 kg and φ=10.0 degrees. However, when the normal force Fhn was strengthened to 90 N or 160 N, Lmin did not varied considerably on the mass mw or the slope angle φ as shown in Figures 4(b) and (c). If Fhn =90 N, the shortest length of Lmin was 0.11 m at mw=10.0 kg and φ=-10.0 degrees, and the longest length of Lmin was 0.24 m at mw=10.0 kg and φ=10.0 degrees. If Fhn =160 N, the shortest length of Lmin was 0.12 m at mw=10.0 kg and φ=-10.0 degrees, and the longest length of Lmin was 0.20 m at mw=10.0 kg and φ=10.0 degrees.
The minimal wheelbase length Lmin was estimated under the assumption of steady walking of a=0.0 m/s2, but it depended on the acceleration of walker movement a as shown in equation (14). The acceleration phase of a>0 was critical because Lmin was lengthened. As described lately in measured data of human factors, the maximal a was 3.9 m/s2 among all the subjects. Therefore, we used three kinds of a: 0.0 m/s2, 2.0 m/s2, and 4.0 m/s2. Table 1 shows the dependence of the minimal wheelbase length Lmin on the acceleration a and other variables. A larger a, a weaker Fhn, and a heavier mw led to a longer wheelbase especially during uphill movement. If Fhn=20 N and mw=10.0 kg, Lmin was 0.22 m during steady walking of a=0.0 m/s2 on the flat road of φ=0.0 deg, but it was lengthened to 0.51 m during acceleration phase of a=4.0 m/s2. It was also lengthened to 0.64 m during acceleration phase of a=4.0 m/s2 on the uphill of φ=10.0 deg.
| mw | 1.0 [kg] | 5.0 [kg] | 10.0 [kg] | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | Fhn φ |
20[N] | 90[N] | 160[N] | 20[N] | 90[N] | 160[N] | 20[N] | 90[N] | 160[N] |
| 0.0 [m/s2] |
-10 [deg] | 0.12 | 0.13 | 0.13 | 0.10 | 0.12 | 0.12 | 0.10 | 0.11 | 0.12 |
| 0 [deg] | 0.16 | 0.14 | 0.13 | 0.20 | 0.16 | 0.15 | 0.22 | 0.18 | 0.16 | |
| 10 [deg] | 0.19 | 0.15 | 0.14 | 0.30 | 0.19 | 0.17 | 0.35 | 0.24 | 0.20 | |
| 2.0 [m/s2] |
-10 [deg] | 0.16 | 0.14 | 0.13 | 0.22 | 0.16 | 0.15 | 0.24 | 0.19 | 0.17 |
| 0 [deg] | 0.20 | 0.15 | 0.14 | 0.31 | 0.20 | 0.17 | 0.37 | 0.25 | 0.21 | |
| 10 [deg] | 0.23 | 0.16 | 0.15 | 0.41 | 0.24 | 0.20 | 0.49 | 0.31 | 0.25 | |
| 4.0 [m/s2] |
-10 [deg] | 0.20 | 0.15 | 0.14 | 0.33 | 0.21 | 0.18 | 0.39 | 0.26 | 0.22 |
| 0 [deg] | 0.24 | 0.16 | 0.15 | 0.43 | 0.25 | 0.20 | 0.51 | 0.32 | 0.26 | |
| 10 [deg] | 0.27 | 0.17 | 0.15 | 0.52 | 0.28 | 0.22 | 0.64 | 0.38 | 0.30 | |
Table 1: Dependence of minimal wheelbase length Lmin [m] on acceleration of walker movement a, slope angle φ, normal force applied at handgrip Fhn, and mass of walker mw. Handgrip height H was 1.0 m. Friction coefficient µ was 0.13.
Second, we described the measured data of two human factors: normal force applied at handgrip Fhn and acceleration of walker movement a in actual usage of walker. Figure 5 shows typical examples of the normal force Fhn and the acceleration a on the flat road. As shown in Figure 5(a), the subject pushed handgrip vertically throughout walking, but a periodical variation was also observed. The dashed line indicated the maximal normal force. The subject did not grasp the handgrip first; therefore, the normal force Fhn was not applied to it before the gait phase. The subject then grasped the handgrip and started to walk by the instruction of the experimenter. The subject also stopped walking at the end of the road and released his or her hands from the handgrip. The normal force Fhn was not applied to the handgrip after the gait phase. The user continued to push the handgrip downward during all the gait stages, but the normal force Fhn fluctuated periodically. In general, the four-wheeled walker accelerated more in gait initiation and decelerated more in gait termination, but the acceleration fluctuated even during steady walking as shown in Figure 5(b). The dashed lines showed the maximal acceleration and the maximal deceleration. Some subjects took the maximal acceleration or deceleration at the stage of steady walking. We extracted the maximal normal force, the maximal acceleration and deceleration from the measured data of the twenty subjects. The maximum values of Fhn and a were not at the same time.
The split-plot factorial design ANOVA on the maximal Fhn indicated that the interaction between the two factors was significant (P<0.01): gender × the slope angle φ, gender × the handgrip height H, and the slope angle φ × the handgrip height H. Figure 6 shows a comparison of the maximal normal force at the handgrip between the factors. The maximal Fhn ranged from 19 N to 163 N. The result of the post-hoc analysis is shown in Table 2. Males applied a larger Fhn to the handgrip than females. A larger Fhn was induced with a lower H for both genders, especially during downhill movement.
| SU | GU | F | GD | SD | ||
| Female | SU | |||||
| GU | n.s. | |||||
| F | n.s. | n.s. | ||||
| GD | n.s. | n.s. | n.s. | |||
| SD | SD>SU | SD>GU | n.s. | n.s. | ||
| Male | SU | |||||
| GU | n.s. | |||||
| F | F>SU | n.s. | ||||
| GD | GD>SU | GD>GU | GD>F | |||
| SD | SD>SU | SD>GU | SD>F | n.s. |
Table 2: Result of post-hoc analysis for maximal normal force applied at handgrip: gender × slope angle. Significant level was set as P<0.01. Slope angle is expressed as steep uphill (SU), gentle uphill (GU), flat (F), gentle downhill (GD), and steep downhill (SD). n.s.: not significant.
Figure 6: Maximal normal force applied at handgrip obtained from ten females and ten males on slope angle (uphill, flat, downhill) and handgrip height (low, middle, high). Maximal normal force was shown as mean value and standard deviation obtained from the data. L, M, and H indicated low height (0.82 m), middle height (0.92 m), and high height (1.02 m) of handgrip, respectively.
The split-plot factorial design ANOVA on the maximal acceleration suggested that the main effect of gender was not significant, while the interaction between the slope angle φ and the handgrip height H was significant (P<0.01). Figure 7(a) shows a comparison of the maximal acceleration. In general, the post-hoc analysis indicated that the maximal acceleration became larger at the middle (0.92 m) or higher handgrip (1.02 m) during downhill movement compared with that at the lower handgrip (0.82 m) during flat or uphill movement. The maximal acceleration was 3.9 m/s2 among all the subjects. As for the maximal deceleration, the main effect of the slope angle φ was barely significant (P<0.01). Figure 7(b) shows a comparison of the maximal deceleration. The post-hoc analysis indicated that the maximal deceleration became larger during steep downhill movement compared with that during movement on other slope angles. The maximal deceleration was -5.1 m/s2 among all the subjects.
Figure 7: Maximal acceleration and deceleration obtained from ten females and ten males on slope angle (uphill, flat, downhill) and handgrip height (low, middle, high). Maximal acceleration and deceleration were shown as mean value and standrad deviation from the data. L, M, and H indicated low height (0.82m), middle height (0.92 m), and high height (1.02 m) of handgrip, respectively. (a) Maximal acceleration. (b) Maximal deceleration.
The normal force applied at the handgrip Fhn and the acceleration of walker movement a were human factors for the determination of the minimal wheelbase length Lmin required for prevention of tipping. The theoretical prediction indicated that Lmin was lengthened with a weaker Fhn during uphill movement as shown in Figure 3. If the walker was on the flat road, the user could move it forward by pushing the handgrip forward just at the friction force, Fht = μFhn, during steady walking (a =0.0 m/s2) as shown in equation (1). During uphill movement, the tangential component of the gravitational force mwgsinφ was applied backward at the center of mass of the walker as shown in Figure 1. The user had to push the handgrip forward at ( cos ) sin ht w hn w F = μ m g φ + F + m g φ . The tangential force Fht was strengthened with the steeper slope angle φ on the uphill because the friction coefficient was much less than 1.0 (μ = 0.13). In other words, the backward component of the gravitational force was applied to the walker on the uphill. In order to overcome this backward force, the user pushed the handgrip forward strongly. If the user weakened Fhn under this control during uphill movement, the ground reaction force in the normal direction at the rear wheels Rrwn was weakened as shown in equation (3). The walker was easily upended by a stronger Fht because the handgrip was higher than the center of mass: H>lcn. However, during steeper downhill movement, Lmin was shortened with a weaker Fhn as shown in Figure 3. The tangential force Fht was smaller or even negative because mw gsinφ was applied forward to the walker. The ground reaction force Rrwn was strengthened, as shown in equation (3), even if the user weakened Fhn under this control during steeper downhill movement. Therefore, the walker was not easily upended. Assuming a fundamental condition of no normal force (Fhn=0.0 N) and no acceleration (a=0.0 m/s2) for simplicity, we could obtain a threshold for the slope angle of φ=-tanμ. On the asphalt road of μ=0.13, the threshold was φ=-7.4 degrees. This angle was the same as the slope angle critical for optimal usage of the walker [2]. The desirable wheelbase length was different between the steeper downhill and the other slope angles. Downhill movement on a low-friction road compelled distinct usage by elderly users as well as distinct wheelbase length from developers.
The relation between Lmin and the acceleration a was linear as shown in equation (14). The experimental result revealed that the walker accelerated more and decelerated more during steep downhill movement than during movement of other slope angles. During downhill movement, the walker was moved forward by the tangential component of the gravitational force mwgsinφ. The walker was accelerated more on the downhill even if the user pushed the handgrip forward at the same force during uphill or flat road movement. In addition, the walker was decelerated more on the downhill because the user pulled the handgrip backward to stop the accelerated walker. However, a longer wheelbase was not obtained by a larger a during steeper downhill movement as shown in Table 3.
| L | M | H | ||
| Female | L | |||
| M | M<L | |||
| H | H<L | H<M | ||
| Male | L | |||
| M | M<L | |||
| H | H<L | H<M |
Table 3: Result of post-hoc analysis for maximal normal force applied at handgrip: gender × handgrip height. Significant level was set as P<0.01. Handgrip height is expressed as lower position (L), middle position (M), and higher position (H). n.s.: not significant.
The experimental result indicated that the maximal Fhn varied with gender as shown in Figure 6. Females produced a weaker Fhn than males. Van der Beek et al. [11] observed the same result for the external forces during the pushing of a wheeled cage by postal workers. Since a female generally had a lower height than a male, the female assumed more upright posture than the male. Female subjects also weighed less than males. Thus, a female subject could keep her lighter upper body in a more upright posture with a weaker Fhn. This result implied that, for a flat road or uphill, a wheelbase should be lengthened for a female user. She could use a walker with a longer wheelbase for high safety and stability.
For both genders, the maximal Fhn was strengthened during downhill movement compared with flat road or uphill movement as shown in Figure 6 and Table 2. This result was consistent with the previous theoretical prediction [2]. Furthermore, a stronger Fhn was induced by a lower handgrip. Previous studies found that the force direction at the handgrip varied from horizontal to vertical when the handgrip was lowered [12-14]. Ishikura [3] found that the vertical ground reaction force applied to the user’s leg decreased with the flexion angle of the hip joint. If the handgrip was lowered, the user assumed a stooping posture and leaned more on the handgrip. The walker was a valuable product for partial weight-bearing gait [3,5]. However, the minimal wheelbase length Lmin was determined by a weaker Fhn, but not by the maximal Fhn.
The minimal wheelbase length Lmin also depended on other factors. The mass of the walker mw was a design factor. The theoretical prediction indicated that Lmin was lengthened especially if the user applied a weaker Fhn of the heavier mw on the steeper uphill as shown in Figure 4. It did not vary considerably on mw under the other conditions. Users preferred a lighter walker because it had high controllability and high mobility in actual walking environments. Therefore, mw was not critical for the determination of Lmin.
The handgrip height H was a design factor. For the walker without wheels, it was recommended that the top of the walker was aligned with the ulnar styloid when the user stood beside the frame with arms held loosely in a relaxed position [9]. In upright posture, the height of the wrist is 48.5 % of the body height from the ground [15]. If the user had the average height of the male subjects of 166.3 cm or the female subjects of 155.8 cm, the handgrip height should be adjusted to 86.7 cm or 75.6 cm. This height was around the lower position of the commercial walker used in the experiment. However, this position was safe because the user pushed the lower handgrip strongly as shown in Figure 6. The minimal wheelbase length Lmin was shortened with the lower handgrip. The higher handgrip led to a longer wheelbase obviously as shown in equation (14) and Figure 1.
The friction coefficient μ was also an environmental factor. In this study, the friction coefficient of the asphalt road was used; however, Lmin should be longer obviously on a high friction road such as gravel as shown in equation (8). The strategy of walker handling varied depending on the road friction [16]. It was not easy for users to handle the walker on a high friction road. The four-wheeled walker was mainly used by elderly users. Therefore, these users should not use the walker on a high friction road in order to avoid the risk of falling.
The wheelbase length of the commercial products of the fourwheeled walker in Japan ranged from 0.49 m to 0.69 m [8]. The commercial walker used in the experiment had a wheelbase of 0.56 m. As shown in Table 1, the mechanical model predicted that the wheelbase length for the higher handgrip of 1.0 m was from 0.16 m to 0.51 m at the flat asphalt road and from 0.19 m to 0.64 m at the steep asphalt uphill of 10 degrees. Except for extreme conditions of a larger acceleration of 4.0 m/s2 and a steeper uphill of 10 deg, the predicted wheelbase length was shorter than the actual wheelbase length of the commercial walkers. In the model analysis, we assumed that the handgrip was positioned just above the rear wheels. However, the handgrip of the commercial walkers was arranged between the front and rear wheels. Many walkers were designed that their handgrip was positioned near the rear wheels. This arrangement was a valid design from an ergonomic point of view because it maintained a margin of walker stability for prevention of tipping.
This study had some limitations in actual usage of the walker. The first limitation was the margin of walker stability. In the model analysis, we assumed that the user walked with the walker on the asphalt road within the sloped surface between -10 degrees to 10 degrees. However, there are the other conditions to consider from this assumption such as small bumps in the boundaries between roadways and sidewalks, high friction roads of gravel, and so on. When safety is considered in actual usage of the four-wheeled walker in an outdoor environment, the margin of walker stability should always be taken into account. This consideration would depend on the environment in which the walker was used. The second limitation was simplification of some phenomena in actual usage of the walker for the model analysis. Since we took into consideration health and safety issues, twenty healthy males and females from 60 to 74 years of age participated in the experiment. However, the walker was also used by elderly users in stooping posture with lower physical characteristics. Since such users would walk slowly, the acceleration of walker movement was small. A stooping user would push the handgrip strongly to maintain a flexed trunk. Therefore, the minimal wheelbase length could be adopted for stooping users because it was shortened with the stronger normal force at the handgrip and the smaller acceleration. However, we proposed that such users should refrain from using the walker on sloped surfaces for safety reasons. The third limitation was consideration of abnormal situations in actual usage of the walker. For example, it would be easy for a user to get over a small bump by lifting the front wheels of the miniaturized walker. However, there would be a high possibility of tripping to occur if the wheels caught such a bump. Further studies considering different factors are required for the application of this study to produce an optimal design of an actual walker.
The minimal wheelbase length was lengthened with a weaker normal force at the handgrip during uphill movement. Female users should use a walker with a longer wheelbase length because they produced a weaker normal force. A longer wheelbase was not obtained by a larger acceleration during steeper downhill movement. The higher handgrip led to a longer wheelbase obviously, and the mass of the walker was not a critical design factor. The minimal wheelbase length was shorter than the actual wheelbase length of the commercial walkers. Many commercial walkers were designed that their handgrip was positioned near the rear wheels. This arrangement was a valid design from an ergonomic point of view because it maintained a margin of walker stability for prevention of tipping. We recommended that a preferable wheelbase length was 0.49 m and longer except for the extreme condition of a larger acceleration of 4.0 m/s2 and abnormal situations of high friction roads or lifting the walker against small bumps.