
Biochemistry & Pharmacology: Open Access
Open Access
ISSN: 2167-0501

ISSN: 2167-0501
Review Article - (2015) Volume 4, Issue 4
In computational chemistry or crystallography, we always meet the problem that requires distributing N particles in one square unit with the minimal neighbor distance. Sometimes this problem is with special or complex constraints. This short article will build a molecular optimization model for the problem, and then will show one example of the application of this model
<Keywords: Computational chemistry, Crystal molecular structure, Optimization model, Optimized Voronoi cells distribution
We consider the problem that requires distributing N (≥ 1) particles in one three- dimensional (3D) 2a × 2b × 2c box/cell/unit with the minimal neighborhood distance. Let us define that dij is the directdistance variable between particle i (1 ≤ i ≤ N) and particle j (1 ≤ i ≤ N, j ≠ i).
Direct-distance means particles i and j have a direct interaction relationship, for example, in computational chemistry, VanderWaals (vdW) contact [1,2], (or) solvent accessible surface area (ASA) contact (en.wikipedia.org/wiki/Accessible surface area), etc to each other. Denote (xi1, xi2, xi3) and (xj1, xj2, xj3) the coordinates of particles i and j, respectively. Then, for the convenience of practical computations [3,4], we can build an optimization model for the above problem.
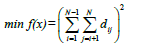 (1)
(1)
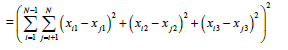 (2)
(2)
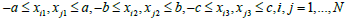 (3)
(3)
This might be a problem of Voronoi diagram (en.wikipedia.org/wiki/Voronoi diagram) and the unit is called Voronoi cell. In computational chemistry, some crystals own special structures of the Voronoi cells; in such a case, we may add some additional constraints to Equation (3).
Clearly, the well-known Lennard-Jones Clusters problem [2] is one case of the above optimization problem Equations (1–3).
We give a 2D Voronoi cells example Figure 1. We distribute 8 particles in one 2D square with the minimal neighborhood distance among them, with a constraint that each particle is only in one of the 8 Voronoi cells of the square. Figure 1(a) shows the initial solution that is given to the problem. Figure 1(b) and Figure 1(c) show the optimal (octagon) distribution of the 8 particles inner the square and onto the boundary of the square, respectively, after we solve the optimization problem Equations. (1-3) if in Equation. (3) “≤” is “≤” Figure 1(b) or “<” Figure 1(c).
Figure 1: The optimization model to distribute 8 particles into 8 Voronoi cells of a square unit: (a) initial distribution given, (b) optimal (octagon) distribution inner the square, and(c) Optimal (octagon) distribution onto the boundary of the square. The green dashed line denotes there is a direct relationship between the two particles they link (e.g. the two atoms have the vdW interactions).
This research was supported by a Victorian Life Sciences Computation Initiative (VLSCI) grant numbered VR0063 on its Peak Computing Facility at the University of Melbourne, an initiative of the Victorian Government (Australia).