Journal of Ergonomics
Open Access
ISSN: 2165-7556
ISSN: 2165-7556
Research Article - (2015) Volume 0, Issue 0
Keywords: Road markings; Speed inducement; Sequence effect; Perceived speed; Discrepancy between objectivity and subjectivity; Hidden Markov model; Driving simulation experiment
Traffic administrators in Japan are devising a variety of road marking patterns designed to reduce vehicle speeds for improved traffic safety. One such pattern consists of transverse lines with progressively reduced spacing to give drivers the impression that their speed is increasing. The road markings verified as inducing a deceleration effect on multi-lane straight roads include “optical dot” roadsurface markings at the Bijogi Junction Saitama-Omiya Line of the Metropolitan Expressway Company [1] and “sequence design” tunnel wall markings in the Inariyama tunnel on the Hanshin Expressway Company’s Kyoto Line [2]. However, we do not well understand how the patterns of progressively reduced spacing in these cases actually induce drivers to decelerate.
We focus on the mechanism by which patterns of sequential transverse and lateral markings induce drivers to decelerate, and test the effectiveness of various markings on a single-lane straight road through in-house experiments with a driving simulator. We define a “sequence pattern” as the alignment of progressively and concurrently reduced spacing of transverse lines on the road surface and lateral poles on the road side, “transverse and lateral markings” as road markings with a sequence patterns, and a “sequence effect” as a vehicle speed inducement effect produced by sequence patterns.
Denton [3-5] provides pioneering research regarding speed inducement mechanisms of road markings with sequence patterns. Conducting an in-house experiment with a driving simulator called a “dynamic visual field generator,” Denton tested the hypothesis that when driving a vehicle over road markings with a pattern of progressively reduced spacing after having adapted to a constant speed on a singlelane straight road, drivers decelerate due to an illusion of acceleration. His research was continued by a number of successors, whose findings included the following: (1) Road markings with sequence patterns may lessen the distribution variance of the platoon speed of several vehicles [6]. (2) Sequence effects may differ over the short and long term [7]. (3) Peak periods of vehicle deceleration may shift with different sequence patterns [8]. (4) The trigger point to remind drivers to slow down may vary with road section length [9]. (5) Shapes such as chevrons, herringbone, and transverse bars may influence sequence effects [10-14]. (6) Tunnel wall markings, sound insulation wall markings, and other lateral markings may have different sequence effects from those of road surface markings [15,16].
Regarding speed reduction markings with progressively reduced spacing to give drivers the impression that their speed is increasing, MUTCD [17] indicates that the sequence pattern itself assumes a key role in the vehicle speed inducement effect. However, we do not necessarily understand the mechanism behind how sequence patterns induce deceleration.
We focus on driver speed perceptions to study mechanisms of the vehicle speed inducement effect, under the assumption of their involvement in discrepancies between perceived and actual speed. In a driving scene where transverse and lateral markings are displayed on the road, optic flows [18] generally cause the driver to perceive movement of objects in the scene at a speed relative to the vehicle speed. We hereby define “perceived speed” as this relative speed perceived by the driver.
This study empirically analyzes discrepancies between actual and perceived speed under the influence of transverse and lateral sequence patterns on a single-lane straight road simulated in in-house experiments, while estimating perceived speed using a hidden Markov model (HMM).
Procedure
We first conduct a driving simulation experiment with a driving simulator (DS) under several types of sequence patterns. In this experiment, vehicle speed transitions are investigated in relation to the sequence patterns.
We then conduct a “perception experiment” to investigate relationships in the change rate between vehicle and perceived speed for a given sequence pattern. In this experiment we prepare two types of recorded moving pictures (MP). The first is a reference MP in which sequence patterns are displayed at a constant speed on the DS screens display. The second is a comparison MP in which the sequence pattern type and MP playback speed differ from the reference MP.
Finally, we use an analytical model to estimate the perceived speed for a given sequence pattern from changes in the vehicle speed. The perception experiment easily analyzes correspondence relationships, but not transitioning. In contrast, the DS experiment easily measures vehicle speed, but not continuous data related to perceived speed. For these reasons, we estimate transitions of perceived speed using a HMM. In this study, the change rate of perceived speed is a discrete latent variable of the HMM and the transition of change rate of vehicle speed observed under each sequence pattern is supervised data of the HMM.
Modeling the markings
We can divide a single-lane straight road with transverse and lateral markings into D sections. Let D be the set of all sections. Transverse lines and lateral poles are located at equally-spaced intervals in each section 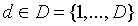 .The degree of the equally spaced intervals in an arbitrary section
.The degree of the equally spaced intervals in an arbitrary section 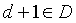 decreases at a rate greater than that in the previous sectiond. Hence, comparing two adjacent sections, the degree of spacing in each section decreases in the direction of vehicle forward movement in D, although there is equal spacing within the limits of each section. This study treats alignment like this as the sequence pattern.
decreases at a rate greater than that in the previous sectiond. Hence, comparing two adjacent sections, the degree of spacing in each section decreases in the direction of vehicle forward movement in D, although there is equal spacing within the limits of each section. This study treats alignment like this as the sequence pattern.
Preparing Q patterns as the sequence pattern, we let Q be a set of all patterns. We define 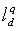 as the interval between markings in
as the interval between markings in 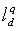 ,locating lines and poles with an arbitrary sequence pattern
,locating lines and poles with an arbitrary sequence pattern 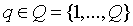 .Then we use
.Then we use 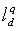 to prepare an indicator defined as
to prepare an indicator defined as  We refer to this indicator
We refer to this indicator 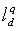 as the “decrease rate” of
as the “decrease rate” of 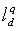
Setting the class
When N drivers respectively drive M times in D, we let and M are the set of all drivers and the set of drive frequencies for each driver, respectively. When driver m∈M drives m times as the m∈M in section d with pattern q, we let  be the average vehicle speed for drive m. In the DS experiment,
be the average vehicle speed for drive m. In the DS experiment, 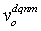 is calculated by averaging the series of instantaneous vehicle speeds measured every 0.02 sec within d. We use
is calculated by averaging the series of instantaneous vehicle speeds measured every 0.02 sec within d. We use 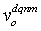 to define
to define 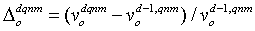 as the “change rate” of the vehicle speed
as the “change rate” of the vehicle speed 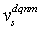 . For the sake of expedience, we define the “perceived speed”
. For the sake of expedience, we define the “perceived speed” 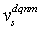 responding according to
responding according to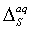 .We also define
.We also define 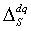 as a change rate of q that is representative of all drivers in section d with pattern q .
as a change rate of q that is representative of all drivers in section d with pattern q .
The problem is that 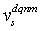 is difficult to directly measure in the DS experiment. Therefore, transitions of
is difficult to directly measure in the DS experiment. Therefore, transitions of 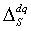 re estimated by an HMM based on observed data for transitions of
re estimated by an HMM based on observed data for transitions of 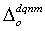 . A HMM is a Markov chain of each discrete latent variable in combination with some discrete observed variables. However,
. A HMM is a Markov chain of each discrete latent variable in combination with some discrete observed variables. However, 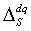 and
and 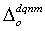 are not discrete, but rather continuous positive and negative rates. We thus propose discretizing to partitions by “class,” as we explain below in detail, to each
are not discrete, but rather continuous positive and negative rates. We thus propose discretizing to partitions by “class,” as we explain below in detail, to each 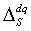 and
and 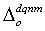 .Accordingly, the class of
.Accordingly, the class of 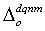 is a discrete latent variable, while the class of
is a discrete latent variable, while the class of 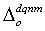 is a discrete observed variable in the HMM. The term “class” means a partition of the change rate of speed over a common range regardless of section, sequence pattern, driver, or drive frequency. We first explain how to partition
is a discrete observed variable in the HMM. The term “class” means a partition of the change rate of speed over a common range regardless of section, sequence pattern, driver, or drive frequency. We first explain how to partition 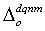 into several classes:
into several classes: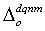 is divided into K parts, each with upper limit
is divided into K parts, each with upper limit 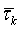 and lower limit
and lower limit 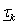 (where
(where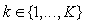 and
and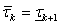 + = ), regardless of d,q,n,m . When
+ = ), regardless of d,q,n,m . When 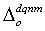 belongs to the
belongs to the 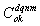 class, we let this class be
class, we let this class be 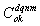 , defined
, defined 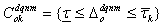 as
as
. To partition 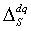 into classes, the number of the class of
into classes, the number of the class of 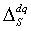 is K, as for
is K, as for 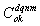 . When kth belongs to the kth class, we let the class be
. When kth belongs to the kth class, we let the class be 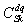 The upper limit
The upper limit 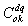 and lower limit
and lower limit 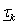 of
of 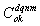 are the same as that of
are the same as that of 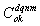
Transition of the perceived speed
We next explain how to estimate transitions of the perceived speed 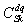 through all sections D for a sequence pattern q : Using the HMM we can estimate a course that the optimal
through all sections D for a sequence pattern q : Using the HMM we can estimate a course that the optimal 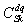 can steer through, to maximize occurrence probability of each
can steer through, to maximize occurrence probability of each 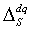 can be estimated. Accordingly, a transition of q can be estimated for a given sequence pattern q given an initial value of
can be estimated. Accordingly, a transition of q can be estimated for a given sequence pattern q given an initial value of 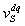 and
and 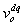 v can be analyzed, where
v can be analyzed, where
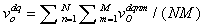
We assume the Markov property for transitions of 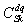 Using conditional probability, this property can be expressed as
Using conditional probability, this property can be expressed as 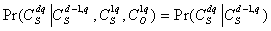 .We let
.We let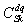 be the transition probability from
be the transition probability from 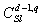 to
to 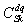 .Assuming that
.Assuming that 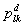 does not depend on
does not depend on 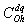 ,we let
,we let 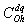 be a homogeneous transition probability. Now, suppose
be a homogeneous transition probability. Now, suppose 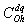 is obtained in d −1 . When we let
is obtained in d −1 . When we let  be an occurrence probability of
be an occurrence probability of 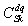 ,the optimal
,the optimal  is calculated by
is calculated by 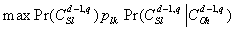 by the Viterbi algorithm [19] and pIk is calculated via the Baum–Welch algorithm [20]. Regarding estimation of
by the Viterbi algorithm [19] and pIk is calculated via the Baum–Welch algorithm [20]. Regarding estimation of  ,we utilize the results of the perception experiment, as explained later in detail. We executed the above calculations using R [21].
,we utilize the results of the perception experiment, as explained later in detail. We executed the above calculations using R [21].
Experimental design
DS Experiment: The roadway displayed on the DS screen represents a two-lane bi-directional intercity expressway typical of Japan. Total width of the roadway is 13 m, comprising two 3.5 m lanes, a 1.5 m median strip, two 1.75 m left shoulders, and two 0.5 m right shoulders. In the transverse and lateral markings illustrated in Figure 1, the width of each transverse line in the direction of vehicle movement is 45 cm, and the length perpendicular to the lane is 3.5 m. The height of each lateral pole is 2.5 m.
Table 1 shows the eight sequence patterns presented to the test subjects. The five sections labeled I–V in Table 1 were preceded by a 600 m run-up section in which the drivers accelerated from speed zero. The length of each section I–V was 100 m, in consideration of habituation effects while driving on the markings. The last 100 m in the run-up section is labeled as section Z in Table 1. We refer to the average speed in section Z as an “initial value” of the speed.
| Section | Z | I | II | III | IV | V | |
| 1 | Interval [m] | 12.00 | 11.40 | 10.83 | 10.29 | 9.77 | 9.29 |
| DR [%] | 0 | 5 | 5 | 5 | 5 | 5 | |
| 2 | Interval [m] | 12.00 | 10.80 | 9.72 | 8.75 | 7.87 | 7.09 |
| DR [%] | 0 | 10 | 10 | 10 | 10 | 10 | |
| 3 | Interval [m] | 12.00 | 10.20 | 8.67 | 7.37 | 6.26 | 5.32 |
| DR [%] | 0 | 15 | 15 | 15 | 15 | 15 | |
| 4 | Interval [m] | 12.00 | 10.20 | 9.18 | 8.72 | 8.28 | 7.87 |
| DR [%] | 0 | 15 | 10 | 5 | 5 | 5 | |
| 5 | Interval [m] | 12.00 | 11.40 | 10.26 | 8.72 | 7.85 | 7.46 |
| DR [%] | 0 | 5 | 10 | 15 | 10 | 5 | |
| 6 | Interval [m] | 12.00 | 11.40 | 10.83 | 10.29 | 9.26 | 7.87 |
| DR [%] | 0 | 5 | 5 | 5 | 10 | 15 | |
| 7 | Interval [m] | 12.00 | 12.00 | 12.00 | 12.00 | 12.00 | 12.00 |
| DR [%] | 0 | 0 | 0 | 0 | 0 | 0 | |
| 8 | Interval [m] | 7.00 | 6.30 | 5.67 | 5.10 | 4.59 | 4.13 |
| DR [%] | 0 | 10 | 10 | 10 | 10 | 10 |
Interval: the interval between markings 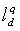 DR: the decrease rate
DR: the decrease rate 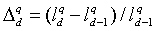
Table 1: The eight sequence patterns.
Each of the eight sequence patterns shown in Table 1 has the following characteristics: Types 1, 2, and 3 have the same respective decrease rates 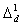 ,
,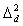 and
and 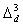 through all sections I–V. Types 4, 5, and 6 have respectively greater decrease rates
through all sections I–V. Types 4, 5, and 6 have respectively greater decrease rates 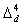 ,
,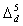 and
and 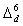 and
and 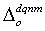 in the beginning, middle, and end sections than in the remaining sections. Type 7 has a zero decrease rate because of its equally spaced intervals. Type 8 has a different initial interval value in Z from the other types, although its sequence pattern is the same as that of type 2. Concerning decrease rates from I to V, any of 5%, 10%, or 15% has been applied to the rates, except type 7.
in the beginning, middle, and end sections than in the remaining sections. Type 7 has a zero decrease rate because of its equally spaced intervals. Type 8 has a different initial interval value in Z from the other types, although its sequence pattern is the same as that of type 2. Concerning decrease rates from I to V, any of 5%, 10%, or 15% has been applied to the rates, except type 7.
The test subjects were five fourth year students at Kobe University, each of whom had a driver’s license. Figure 2 shows a scene from the experiment. No speedometer is displayed on the DS screen during the experiment, although Figure 2 shows one for convenience. The tests were run three times for each sequence pattern. The experimenter instructed each subject to maintain a constant speed while looking into the far distance along the road in the DS screen.
Perception experiment: The experimenter prepared a baseline MP displaying markings at 12 m intervals and displayed at a fixed speed of 70 km/h. The baseline MP was created from a transcription of a driver running at a fixed speed in the type 7 sequence pattern. The experimenter also prepared comparison MPs for contrast with the baseline MP. The experimenter told test subjects the interval and playback speed values of the baseline MP, but not those of the comparison MPs.
We prepared 32 comparison MPs, shown in Table 2. The experimenter showed each subject the baseline MP for 3 s, then each of the 32 cases for 3 s in random order. Subjects immediately chose upper and lower playback speed limits for the comparison MP to estimate speeds in 2 km/h increments in the range 44–100 km/h. This process was repeated nine times, and we took the median value of the upper and lower limits chosen by the subject as the perceived speed of the subject.
| Case | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| DR [%] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Speed [km/h] | 55 | 60 | 65 | 67 | 69 | 70 | 72 | 75 |
| Case | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| DR [%] | 5 | 5 | 5 | 5 | 5 | 5 | 5 | 5 |
| Speed [km/h] | 55 | 60 | 65 | 67 | 69 | 70 | 72 | 75 |
| Case | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| DR [%] | 10 | 10 | 10 | 10 | 10 | 10 | 10 | 10 |
| Speed [km/h] | 55 | 60 | 65 | 67 | 69 | 70 | 72 | 75 |
| Case | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| DR [%] | 15 | 15 | 15 | 15 | 15 | 15 | 15 | 15 |
| Speed [km/h] | 55 | 60 | 65 | 67 | 69 | 70 | 72 | 75 |
DR: the decrease rate 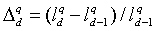 Speed: the comparison speed as contrasted with the baseline.
Speed: the comparison speed as contrasted with the baseline.
Table 2: 32 moving picture comparisons.
Results of the experiments
Figure 3 shows vehicle speed data obtained in the DS experiment. Since the DS measured instantaneous vehicle speed every 0.02 s, we averaged all spot speeds per number of data within each section. We refer to this as the “average spot speed.” Each subject ran each sequence pattern three times in the DS experiment. We hereinafter refer to an average of the three average spot speeds as a “section speed” of the vehicle. Because each subject tried to drive at a constant speed but without reference to a speedometer, the section speeds are distributed as shown in Figure 3.
In Figure 3, in sequence patterns 3, 4, 5 and 6 in which the decrease rate of line and pole spacing was 15% in all intervals, in the first intervals, in the middle intervals and in the last intervals, respectively, each standard deviation of section speed of five subjects has a large value in the section in which the decrease rate was set at 15%. In sequence pattern 7 in which spacing was equal 12m in all intervals, each transition of section speed of five subjects stays relatively steady and each standard deviation of section speed has a small value in all sections.
Figure 4 shows the relationship between subject- perceived speeds and the playback speed of comparison MPs, that is, vehicle speed. Figure 4 displays nine dots for each of the four decrease rates because each subject performed each test nine times. Each dot indicates the average value of five subjects in the eight cases belonging to the same decrease rate in Table 2. Figure 4 shows that the subjects had a propensity to overestimate vehicle speed, regardless of the marking decrease rate.
Results of the estimation
Considering the results of a goodness-of-fit test on the data obtained from the DS experiment (Table 4), we used the seven classes shown in Table 3. Values for the change rate of vehicle speed 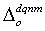 were statistically identical among the decrease rates
were statistically identical among the decrease rates  represented as 5%, 10%, and 15% in Table 4, so we set the upper and lower limits of each class as shown in Table 3. The *, **, and *** symbols in Table 4 indicate that the null hypothesis is rejected at 10%, 5%, and 1% levels of significance for a two-sided test, respectively. For instance, in the case of class 2, where the P value of a chi-square test was 0.053, the null hypothesis “the value of
represented as 5%, 10%, and 15% in Table 4, so we set the upper and lower limits of each class as shown in Table 3. The *, **, and *** symbols in Table 4 indicate that the null hypothesis is rejected at 10%, 5%, and 1% levels of significance for a two-sided test, respectively. For instance, in the case of class 2, where the P value of a chi-square test was 0.053, the null hypothesis “the value of  is statistically independent for each
is statistically independent for each 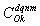 in the class” was regrettably rejected at the 5% level of significance. In general, however, the null hypotheses are not rejected for most classes at least at a 1% level of significance.
in the class” was regrettably rejected at the 5% level of significance. In general, however, the null hypotheses are not rejected for most classes at least at a 1% level of significance.
Since we have seven classes, the data series of 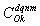 can be obtained from the results of the DS experiment. We applied the Baum–Welch algorithm to the data series to estimate plk .
can be obtained from the results of the DS experiment. We applied the Baum–Welch algorithm to the data series to estimate plk .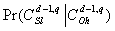 estimated from the results of the perception experiment, we can calculate
estimated from the results of the perception experiment, we can calculate 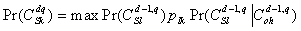 using the Viterbi algorithm. From the upper limits of
using the Viterbi algorithm. From the upper limits of 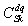 and the initial value of
and the initial value of 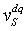 ,the transition of
,the transition of 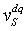 can be estimated for each sequence pattern.
can be estimated for each sequence pattern.
From the above, as shown in Figure 5 we found the characteristics of discrepancy between actual and perceived speed for each sequence pattern.
| Class | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| UL(%) | -100 | -8 | -4 | -2 | -1 | 0 | 3 |
| LL(%) | -8 | -4 | -2 | -1 | 0 | 3 | 100 |
UL: the upper limit 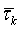 in class
in class  LL: the upper limit
LL: the upper limit 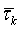
Table 3: Class settings.
| Class | Number of  for each of the three for each of the three |
P value of test test |
|||
| 5% | 10% | 15% | |||
| 1 | 4 | 10 | 7 | 0.276 | |
| 2 | 32 | 49 | 30 | 0.053 | * |
| 3 | 50 | 57 | 34 | 0.052 | * |
| 4 | 44 | 55 | 29 | 0.018 | ** |
| 5 | 53 | 43 | 27 | 0.015 | ** |
| 6 | 33 | 26 | 16 | 0.054 | * |
| 7 | 18 | 12 | 1 | 0.001 | *** |
| Total | 234 | 252 | 144 | ||
Table 4: Goodness-of-fit test for classes.
Figure 5 shows the perceived speed for a given sequence pattern and vehicle speed. As that figure shows, the following characteristics were found in the relationship between perceived and actual vehicle speed.
Except for sequence patterns 1 and 5, perceived speeds were significantly higher than actual vehicle speeds. Perceived speeds for sequence patterns 1 and 5, in contrast, were estimated to decrease gradually with vehicle speed. In sequence pattern 7, which has equally spaced intervals, perceived speed was estimated to gradually increase above the vehicle speed, despite the vehicle speed being constant. In sequence patterns 2 and 8, which both had the same 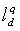 in sections I–V and different initial
in sections I–V and different initial 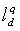 in section Z, the difference in the initial interval influenced the perceived speed.
in section Z, the difference in the initial interval influenced the perceived speed.
Our experiments resulted in five main findings:
• In a sequence pattern in which decrease rate of line and pole spacing was equal 5% in all intervals and one where decrease rate of spacing was greatly increased in the middle intervals, the perceived vehicle speed tended to descend.
• In most sequence patterns other than those above, the perceived vehicle speed was higher than the actual speed.
• In two sequence patterns in which decrease rates of spacing were respectively 10% and 15% in all intervals, trend of the perceived vehicle speeds was different from that in a pattern where decrease rate of spacing was equal 5%.
• In a sequence pattern in which decrease rate of spacing was greatly increased in the first intervals, vehicle speed rapidly decreased while the perceived speed remained high.
• In a sequence pattern in which spacing was equal 12m in all intervals, vehicle speed did not nearly change while the perceived speed was greatly increased.
Several outstanding issues remain. We need to examine vehicle speed behavior at a given perceived speed, the opposite case of the situation examined in this study. We also need to empirically analyze differences in sequence pattern effects that give drivers the impression that their speed is increasing, and the feeling of speed that the DS itself invokes. Finally, we need to study the impact of rapid deceleration of a lead vehicle on following vehicles after the lead vehicle encounters transverse and lateral markings, and whether a resulting accident is a concern.
This work was supported by JSPS KAKENHI Grant Number 25420548, and also by a grant from the Express Highway Research Foundation of Japan.