Journal of Geology & Geophysics
Open Access
ISSN: 2381-8719
ISSN: 2381-8719
Research Article - (2014) Volume 3, Issue 3
Velocity calibration and estimation of microseismic event location are two important ingredients in microseismic monitoring. It is generally considered that the accurate estimation of microseismic event location depends on the accurate velocity structure. In this paper, very fast simulated annealing (VFSA) is first applied to invert velocity structure between the treatments well and the monitoring well by using perforation shot travel time data, and then is implemented to locate the microseismic events using the velocity structure obtained above. Unlike previous applications of VFSA using the objective function of misfit between the theoretical travel time and the observed travel time, we propose a novel objective function for VFSA which consists of the travel time differences of P-wave first arrivals between seismic traces. The P-wave first arrival travel time is calculated by means of a shooting ray tracing method. To illustrate the efficiency of the proposed method, a flat-layered model test is performed by considering the uncertainty of travel time picking. The numerical results indicate that the predicted microseismic event locations have a good match with the true values although the inverted velocity structure is not so accurate.
Keywords: Velocity calibration, Microseismic event location, Very fast simulated annealing
Over the last ten years, the huge growth in unconventional reservoirs (e.g. shale gas, tight gas and tight oil) has caused a significant interest in microseismic fracture monitoring [1,2]. Meanwhile, we are facing the enormous challenges of improving microseismic event locations and building accurate velocity model [3-5]. Various linear inversion techniques (e.g. least square and Singular value decomposition (SVD)) are performed to invert velocity structure and locate microseismic events by using first arrival travel times and particle motion of seismic P and/or S waves [3,4,6-11]. However, those linear inversion methods strongly depend on the initial models that may lead to trap in local minimum [5] due to less receiver coverage (<15 geophones in the monitoring well).
Simulated annealing (SA) is a heuristic optimization approach which may obtain the global minimum [12]. Some authors have applied SA to solve seismic inversion problems such as reflection travel time inversion [13,14], tomography [15], waveform inversion [16], and earthquake location prediction [17]. SA also shows advantages over another global optimization method, genetic algorithm [18]. In contrast to mentioned linear inversion methods using travel time data, SA is a nonlinear inversion method and does not need to calculate the partial derivatives of travel time to unknown parameters (e.g. velocity and density). However, a disadvantage of SA is large computational cost. To improve SA’s efficiency, Ingber [19] proposed a very fast simulated annealing (VFSA) method which has been used in solving various geophysical problems (Zhao et al.; Misra and Sacchi; Pei et al.; Sharma, [5,20-22].
Pei et al. applied VFSA to invert velocity structure through presenting a joint objective function of first arrival travel time misfits between the synthetic data and the observed data of both seismic P- and S-waves. The origin time of perforation shot was assumed to be known in their study. However, the origin time of perforation shot is difficult to measure accurately [3]. To reduce the effect of the origin time of perforation shot, we develop a novel objective function for VFSA which consists of the travel time differences of P-wave first arrivals between seismic traces. The P-wave first arrival travel time in isotropic media is calculated by a modified shooting ray tracing which was originally presented for source-geophone geometry of seismic surface survey in anisotropic media [14,23]. In contrast to only invert velocity model in Pei et al. [5], in this study, VFSA is first applied to invert velocity structure between the treatments well and the monitoring well by using perforation shot data, and then is performed to estimate the microseismic event locations by using the above inverted velocity model. The numerical study demonstrates that the estimated microseismic event locations are very close to the true locations although the inverted velocity structure is not as accurate as we expected.
Figure 1 shows the sketch of microseismic monitoring in which the geophones are cemented in a vertical monitoring well. Each layer represents an isotropic medium. The inverse triangle and hollow circle denote geophone and source, respectively. One can observe that the first arrival travel time received by a geophone is the minimum of the travel times between the direct wave and the refraction wave in regard to source-geophone geometry and velocity contrast (assuming constant density in the model). Given zero to Thomsen anisotropic parameters (ε=δ=0) [24], the anisotropic shooting ray tracing developed in Chen et al. and Chen [14,23] is modified to calculate P-wave first arrival travel time in isotropic media based on the borehole source-geophone geometry of microseismic monitoring. The angles of seismic incidence, transmission and refraction at each interface obey Snell’s law.
To increase the computational efficiency of simulated annealing (SA), very fast simulated annealing (VFSA) was proposed by Ingber [19] to update unknown parameters (e.g. velocity and density) using Cauchy probability distribution which has a sharper crest than original Gaussian distribution used in SA [14]. VFSA takes a lesser amount of computational cost than SA, which makes VFSA reaches the final temperature rapidly. The important control parameters of VFSA include initial temperature choice, temperature cooling (decreasing) rate, acceptance criteria and iteration termination/stop criteria [5,22,25]. Here, to reduce the effect of the origin time of the perforation shot, we present the new objective function E of VFSA which consists of the travel time differences of P-wave first arrivals between seismic traces:
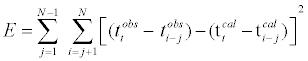 (1)
(1)
where 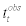 and
and 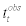 are the observed and theoretical first arrival travel times received at ith geophone, respectively; N is the total number of geophones; j is the gap number between any two geophones. Our goal is to minimize the above objective function (equation 1).
are the observed and theoretical first arrival travel times received at ith geophone, respectively; N is the total number of geophones; j is the gap number between any two geophones. Our goal is to minimize the above objective function (equation 1).
The implementation steps of VFSA are as follows:
• Under initial temperature T , calculate the objective function E (equation 1) using given initial unknown values xk (k=1, M) (e.g., velocity and microseismic location), M is total unknown parameters;
• Adjust unknown value xk through random change Δxk by
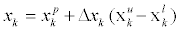 (2a)
(2a)
and
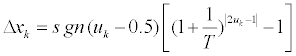 (2b)
(2b)
where 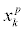 is previous value of xk,
is previous value of xk, 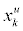 and
and 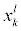 are upper bound and lower bound of xk, respectively, uk varies between 0 and 1, Δxk varies between -1 and +1; then calculate the new objective function E1;
are upper bound and lower bound of xk, respectively, uk varies between 0 and 1, Δxk varies between -1 and +1; then calculate the new objective function E1;
• Determine the probability p for accepting the new unknown values using the following either criterion
E1 – E < 0, (3a)
exp - (( E1 - E) / T > uk (3b)
• Define half temperature T as cooling rate.
• Repeat steps 2) - 4) until the annealing converges where the error between successive unknown values is less than a very small value (e.g., 0.00001), or the iteration number reaches to a given large number (e.g., 10,000).
A flat-layered 2D model with size 700m x 2550m is used in this test [11]. The P-wave velocity and depth of each layer are listed in Table 1. A total of twelve geophones (inverted triangle) are placed in a deviated monitoring well (Figure 2). The perforation shot (cross) and other four induced microseismic events are arranged in this model. The origin time of the perforation shot is 100s, whereas the origin times of other four microseismic events are 130s. The P-wave first arrival times for perforation shot and other microseismic sources are calculated by a modified seismic ray tracing [11,14,23]. The figure 3 shows P-wave first arrival travel time calculated for perforation shot. Very fast simulated annealing (VFSA) method is used to separately invert velocity structures using P-wave first arrival travel times with and without noise emitted from perforation shot. As processed in Pei et al. [5], the noisy travel time data are generated by adding Gaussian noise with a standard deviation of ±0.5ms to the synthetic travel time data. The initial temperature is 20 based on several tests. The maximum iteration number is 10000. The initial velocity of each layer can be any value in 10% error range of real velocity. Figure 4 shows the inverted velocity structures using both travel time types of perforation shot (with and without noise). One can observe that the inverted velocity model obtained from noise-free travel time data is very close the real model, whereas the one obtained from noisy travel time data has big deviation from the true model, especially for the third layer of the model. By using the velocity structures obtained above, we again implement VFSA to invert the locations of perforation shot and other four microseismic events. We choose the same VFSA control parameters as used in above velocity inversion. The initial location of each microseismic source can be any value in 10% error range of real microseismic location. Table 2 presents the comparison between inverted locations (noise-free travel time inversion) and true locations. One can tell that the inverted location of each source (perforation shot or microseismic event) has a great agreement with the true location. In addition, we also can get better location results although the velocity model obtained by noisy travel time data has big deviation from the true events are very close to the true locations.
| Layer no. | Depth (m) | Vertical P-wave velocity (m/s) |
|---|---|---|
| 1 | 2200 | 4000 |
| 2 | 2300 | 4266 |
| 3 | 2350 | 4457 |
| 4 | 2400 | 4600 |
| 5 | 2480 | 4457 |
| 6 | 2550 | 4756 |
Table 1: Physical properties for the flat-layered model.
| True locations | Inverted locations without noise | |||
|---|---|---|---|---|
| X(m) | Z(m) | X(m) | Z(m) | |
| Perforation shot | 550 | 2450 | 550.3 | 2450.2 |
| Event-1 (S1) | 450 | 2375 | 450.1 | 2375.4 |
| Event-2 (S2) | 530 | 2420 | 528.3 | 2419.9 |
| Event-3 (S3) | 530 | 2470 | 531 | 2470.2 |
| Event-4 (S4) | 580 | 2470 | 580.8 | 2470.3 |
Table 2: The inverted locations by using very fast simulated annealing (VFSA) method. The picked P-wave first arrival travel times are assumed noise free.
Figure 2: The sketch of a flat-layered velocity model (Adapted from Chen et al., 2013). 12 geophones are placed along a deviated well. The inverted locations of perforation shot and other four microseismic events are obtained by very fast simulated annealing (VFSA) method through adding Gaussian noise with a standard deviation of 0.5ms to the synthetic travel times.
Very fast simulated annealing (VFSA) is implemented to invert velocity structure and locate the microseismic events. The objective function of VFSA consists of the travel time differences of P-wave first arrivals between seismic traces. Our numerical results show that the good estimation of microseismic event locations may be obtained although velocity structure is not so accurate. This proposed method will be further applied to invert velocity model and locate the microseismic events in anisotropic media.
The authors would like to thank Professor Shashi Prakash Sharma for useful help. We also thank two anonymous reviewers for their constructive comments which greatly improve our paper.