Advanced Techniques in Biology & Medicine
Open Access
ISSN: 2379-1764
ISSN: 2379-1764
Research Article - (2016) Volume 4, Issue 2
Intrauterine Growth Restriction, the poor growth of the fetus during pregnancy is a medical difficulty exposing the fetus to severe complications which could lead to its death. The discrimination of such medical problem is still challenging. This work aims to improve the discrimination between Intrauterine Growth Restricted fetuses from healthy fetuses, by comparing Unbiased Recurrence Plot analysis of their heart rates to standard recurrence plots. It also aims to offer the ultimate recurrence quantification parameter that leads the best discrimination. Entropy parameter, determinism, cross-determinism, recurrence rate and percentage of reduced sojourn points are computed from Unbiased Recurrence Plots. The evaluation of the effectiveness of discrimination is carried out using the sensitivity, specificity, accuracy and precision and Cohen’s kappa coefficient from the recurrence quantification analysis, and is compared to standard recurrence plots. Experimental results showed that the cross-determinism parameter is the utmost parameter providing a high discriminative power (86.5%) and the maximum relative separation between the two fetal heart rate sets (42.6%), and minimum standard deviation (± 0.12%). Both recurrence rate and entropy parameters are less active than cross-determinism but they are still adequate for Intrauterine Growth restricted fetuses classification. These results pave the way for highly sensitive classification devices. However, the detection of other medical problems should be further investigated, and deeper link of quantification parameters to distress diagnosis should be considered in order to understand the underlying physiological processes.
Keywords: Recurrence plots, Unbiased recurrence plots, Recurrence quantification analysis, Post processing, Intrauterine growth restriction, Discrimination, Doppler ultrasound fetal heart rates
• Detection of Intrauterine Growth Restriction using Unbiased Recurrence Plots of Fetal Heart Rates;
• Computation of entropy, recurrence rate, determinism, cross-determinism and the percentage reduced sojourn point parameters;
• Computation of the sensitivity, specificity, accuracy and precision of the recurrence quantification parameters in the discrimination of Intrauterine Growth Restricted fetuses.
• Calculation of the discriminative power using Cohen’s Kappa Coefficient.
• Providing the recurrence quantification parameter leading the utmost detection of Intrauterine Growth Restricted fetuses;
Intrauterine Growth Restriction (IUGR) that is the poor growth of the fetus during pregnancy is a medical problem striking the women and subjecting its fetus to severe problems which could lead to its death. IUGR that may be due to respiratory, neurological and cardiovascular causes is still challenging [1]. Complexity analysis of fetal heart rate (FHR) recordings are constantly developed to discriminate distressed fetuses due to IUGR. Such complexity techniques have been employed to detect and classify signals into healthy and distressed classes [2-10].
Significant complexity analysis tools have been rendered to detect the discussed medical problem and to avoid fetal death. Some of these were quantitative, such as the entropy (En) analysis and types including, but not limited to, the approximated entropy, sample entropy, fuzzy entropy and recently n-order entropy [4,5,7,8,11]. Other methods were qualitative such as the Recurrence Plots (RPs) and their corresponding Recurrence Quantification Analysis (RQA) [2,3,10]. Chen et al. showed that RQA measures are more accurate than the standard entropy analysis techniques in detecting biomedical time series states [12]. Recurrence Plots introduced in our previous work [2,3] have shown their usefulness in detecting fetal distress due to IUGR. These plots were Unbiased Recurrence Plots (URPs) applied to Fetal Heart Rates (FHRs) in order to (i) validate the performance of the cutting- edge removal of sojourn points, i.e. false recurrences contaminating RPs, and (ii) demonstrate URPs on a healthy FHR (H-FHR) and a single distressed FHR (D-FHR) recording during IUGR. The former work provides the best recurrence plot and quantification parameter that ultimately discriminate IUGR.
The difference between the work we showcase in this paper and our previous work [3] is basically in the application part, the used RQA parameters and the mode of evaluating the discrimination. In Zaylaa et al. [2,3] we have validated URPs on the logistic map and a single healthy and a single distressed fetuses. This paper demonstrates the application of URPs to a larger database composed of 50 FHRs (25 H-FHRs and 25 IUGR-FHRs). It also investigates the performance of additional RQA parameters including the unbiased recurrence rate (RR) and En measurements in the discrimination between healthy and distressed FHRs. This study aims also to provide the discriminative power using Cohen’s kappa coefficient scores. The entropy parameter is introduced and computed from RPs to compare its performance in detecting IUGR. Moreover, the entropy is compared to the determinism (DET), recurrence rate (RR), cross-determinism (CDET) and percentage reduced sojourn points (PRSPs). The evaluation of the results is highlighted using the two statistical parameters: the relative separation or relative error RE and the standard deviation (SD). The sensitivity, specificity, accuracy and precision of classification of IUGR and healthy fetuses were carefully evaluated from RQA parameters.
The paper is organized as follows; section 2 introduces the materials and methods, multi-channel doppler ultrasound machine and recurrence plot methods, in addition to the parameters and entropy quantification. Section 3 sets out the results, section 4 discusses the results and provides the conclusion.
System and fetal heart rate data
Multichannel doppler ultrasound recordings and fetal heart rates: Multi-channel Doppler Ultrasound (MCDUS) device is the system used for monitoring FHRs. MCDUS (ALTHAÏS Technologies, Tours University, France) is a portable device connected to a personal computer (PC) (Figure 1). MCDUS comprised three groups of four transducers (12 probes × 5 gates) (bottom left and right Figure 1) and a Doppler acquisition board. The operating functions of the acquisition board (1-6) were explained in details in [13]. One group of Doppler system electrodes was dedicated to explore the fetus heart. The transducers exploring the fetus heart are non-focused and monoelement. They are circular with a diameter of 13.5 mm each, and their acoustic power is 1 mW/cm2. Geometrically, each electrode comprises transducers located at the top of an equilateral triangle of side 40.7 mm and at its center (Figure 1).
Figure 1: Actifoetus Doppler Ultrasound Device (top). The electronic Multi-Channel Doppler acquisition unit connected to three identical electrode sets and the computer (bottom left). Top view of an electrode set composed of four transducers (bottom right). Bottom view of the electrode set composed of four transducers. One electrode was dedicated to detect the fetal heart rate.
Two typical FHRs of the control subjects (healthy) and distressed subjects are displayed in Figure 2, these FHRs are then windowed and 3-minute sub-FHRs are produced. Figure 2 showcase (a) a H-FHR and (b) a D-FHR shown in gray. According to the medical standards the healthy fetal heart rate ranges between 110 beats per minute (bpm) and 160 bpm during the third trimester [14], i.e. between the 28th and 40th week of pregnancy (Figure 2).
Clinical study and protocol: MCDUS transducers are placed on the mother’s abdomen and adjusted to transmit a sinusoidal pulse at 2.25 MHz with a Pulse Repetition Frequency (PRF) of 1 KHz. US is transmitted to the fetus heart through the mother’s abdomen. During its transmission it interacts with the moving structures of the heart, such as, the walls and valves. This interaction modifies the transmitted frequency of the pulse. The frequency content of the backscattered signal carries the heart signature when recorded from a volume containing the fetus heart. Doppler signals are processed numerically and FHR datasets are estimated, however, the estimation is beyond the scope of this work and result from the methods discussed in [15,16].
Our database includes 50 FHR strips collected by MCDUS from 50 pregnant women. The women were in their third trimester and the average fetal age of the entire database was 29 ± 1 week. Recordings were obtained at Bretonneau Hospital (CHRU) in Tours, France. The consent of each patient was obtained and the study was approved by the ethical committee of the Clinical Investigation Center for Innovative Technology of Tours (CIC-IT 806 CHRU of Tours).
Signal post-processing
Recurrence plots and recurrence quantification parameters: An RP is a two-dimensional visualization of recurrences of the system state Xi with another Xj. When expressed for a threshold of recurrence r, a black dot signifies a recurrence of the states at (i,j) and a white dot signifies a non-recurrence of states.
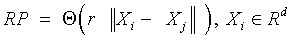 (1)
(1)
where
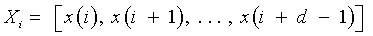 (2)
(2)
and Xi ∈ Rd are the points in the phase space at which the system is situated at time i, i, j ∈
{1, . . . , N−d+1 }, N is the total number of points, d the embedding dimension [17-20], Θ (•) the Heaviside function and ||.|| the L∞ norm. The main diagonal line showcases the identity of the signal. Diagonal lines indicate deterministic behavior, regular patterns of parallel lines reveal a periodicity. Isolated points (islands) are typical for chaotic systems, while a rectangular patch results from laminar states [21].
After reproducing the two standard qualitative RPs, these RPs were extended by the computation of scalar quantitative parameters called the Recurrence Quantification Analysis (RQA) [22]. The first quantitative parameter used in this work is the determinism in percentage (%DET), as it seemed efficient in the detection of system transitions [3,18,19,21]. %DET is a simple quotient of the number of RP points that lie on lines of the assumed minimal length (parallel to the main diagonal) to the total number of black RP points. %DET is given by [18,23-28] as:
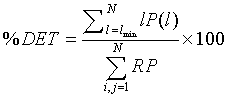 (3)
(3)
Where P (l) is the histogram of length l and lmin the minimum length of a diagonal line, i.e., the number of points forming a diagonal line of at least length lmin. The second parameter used is the cross-determinism (% CDET), proposed by our previous work [2,3], as it seems powerful in detecting healthy-distressed FHR transition. % CDET is used to quantify false recurrences also known as sojourn points, which result from oversampling the trajectory of the dynamics of the studied system and appear as lines perpendicular to the Length of Identity (the main diagonal of the plot) in RPs [3,19], and it is defined by:
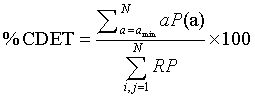 (4)
(4)
Where P(a) is the number of cross-diagonal lines, i.e. lines perpendicular to the main diagonal, of length a, a min the minimum length of cross-diagonal lines. The third parameter is the Percentage of Reduced Sojourn Points (PRSP) calculated from %CDET as: (100%−% CDET) to quantify the percentage of reduced false recurrences from RPs as proposed in our previous papers [2,3]. The fourth parameter is the recurrence rate RR, which measures the density of recurrence points in the RP [19,23,29], is used and defined in percentage by:
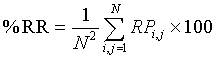 (5)
(5)
according to [18]. Finally, the fifth parameter is the Entropy measure which refers to the Shannon’s entropy [19,23,27]. It measures the sum of the bin probability of distribution of each diagonal line for each nonzero bin.
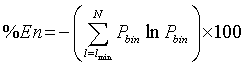 (6)
(6)
where Pbin= P(l)/Nl and Nl is the number of points constituting a diagonal of length l.
For biological systems exhibiting a complex behavior an important advantage of RQA is that no assumptions on the time series are required, such as linearity for instance in Fourier transforms [30]. The former RQA parameters are extracted from the features of RPs, however as there are two RPs of standard use [18,31] and three URPs recently developed in our previous work [3], it was essential to describe the five RP techniques that were utilized in this paper.
Unembedded recurrence plot: The first standard recurrence plot model to analyze signals such as FHRs is the unembedded recurrence plot. It is the matrix given by Eq. 1 for d=1 [31,32] and is denoted RP1 in this paper.
Embedded recurrence plot: The second standard recurrence plot model to analyze heart rates is the unembedded recurrence plot. It is the matrix given by Eq. 1 for d ≥ 2 [18] and is denoted RP2 in this work. Both d and τ are set from an empirical inference, i.e. from RPs based on embedding the time series (RP2), where d=3 and τ obtained from the autocorrelation function as proposed by Marwan et al. [18,19] (Figure 3).
Unbiased recurrence plots: The first URP is the embedded RP with special setting parameters introduced in our previous work [3] such that, the embedding dimension d and time delay τ are selected were the CDET parameter is minimum. Herein, the optimal embedding dimension dopt is set at 2 and the optimal time delay τopt [3]. The corresponding RP is denoted RP3 and computed using Eq. 1 for the former and the latter setting parameters (dopt, τopt).
The second URP is derivative-based RP introduced in our previous work [3]. It is obtained from Eq. 1 for xj = xi thereby it is called derivative-based and denoted RP4.
The third URP is the 2-time pattern RP introduced in our previous work [3], it is denoted RP5 and constructed using Eq. 1. Figure 3 showcase a block diagram of the RP techniques used in this study and their Recurrence Quantification Analysis (RQA). Figure 3 is divided into two parts, black and red dashed boxes. The black dashed box constitutes the RP post-processing time series techniques that existed in literature. Based on the bibliography, the results of RQA were either biased (top) or empirically unbiased (center) [18,19,31]. Whereas, the red dashed box highlights our
URP complexity analysis, such that, by referring to the numerical simulations the results of RQA were of reduced bias due to the elimination of sojourn points [2,3].
Both the embedding dimension d and the time delay τ in Figure 3 reflect the setting parameters for most of RPs, and m stands for the number of patterns, the former and latter parameters are a must for the construction of most RPs (Figure 4).
Statistical tools for evaluating the discrimination
Sensitivity, specificity precision and accuracy: Statistical measures including the sensitivity, specificity, precision and accuracy of discrimination were computed. The former task computed from the RQA parameters extracted from the five RP methods.
• True Positives (TP) are IUGR-FHRs correctly identified as distressed;
• False positive (FP) are healthy FHRs incorrectly identified as distressed;
• True Negatives (TN) are healthy FHRs correctly identified as healthy;
• False negative (FN) are IUGR-FHRs incorrectly identified as healthy.
The different statistical parameters used are defined as given in Table 1. The total number of bars and events identified, it is denoted Mt and equal to 10 (Table 1).
| ED(RQA) | Formula |
|---|---|
| Sensitivity | 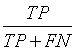 |
| Specificity | 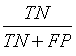 |
| Precision | 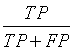 |
| Accuracy | 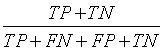 |
| Discrimination Power | 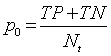 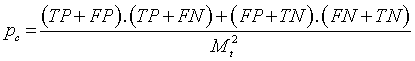 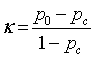 |
Table 1: The statistical parameters used to evaluate the discrimination.
Discriminative power: To evaluate the discriminative power of each RQA parameter, the power used to discriminate healthy and distressed classes using the five RP models, we need a score that indicates the separability of the classes. Cohen’s Kappa coefficient κ, a metric calculated according to Table 1 [21,33].
Relative error and standard deviation: To evaluate the performance of diagnosis or discrimination of the fetus medical state while taking the full advantage of the nonlinearity of FHR time series, both the absolute Relative Separation/Error (RE) and the Standard Deviation (SD) were calculated as in [34]. The absolute RE is given as:
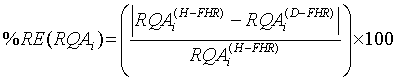 (7)
(7)
where i={1, .., 5} and RQA’s are DET, CDET, PRSPs, RR and En. A null absolute RE, i.e. 0% relative difference between the healthy and IUGRfetuses datasets, signifies that the two sets are not classified. In contrary, a 100% absolute RE signifies that the two sets are ideally classified.
SD that measures the amount of RQAi dispersion from its average value is given as follows:
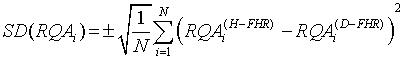 (8)
(8)
where N is the total number of FHRs used.
Of all the FHR database available, URPs were applied on 25 H-FHRs and 25 IUGR-FHRs to amend the discrimination between IUGR fetuses and healthy fetuses. Simulations were carried through Matlab environment.
Intrauterine growth restriction detection from fetal heart rates
This subsection provides both the qualitative and the quantitative results of the evaluation of the diagnosis of intrauterine growth restricted fetuses from healthy fetuses (Figure 5).
Figure 5: The unbiased recurrence plots of FHRs. (a) The 3 − d embedded recurrence plot with specific settings RP3 of H-FHR. (b) The 3−d embedded recurrence plot with specific settings RP3 of IUGR-FHR. (c) The derivative-based recurrence plot RP4 of the H-FHR. (d) The derivative-based recurrence plot RP4 of the IUGR-FHR. (e) The m-time pattern recurrence plot RP5 of the H-FHR. (f) The 2-time pattern recurrence plot RP5 of the IUGR-FHR.
RP evaluation of discrimination: Figures 4 (a) and 4 (c) represent RP1 and RP2 of a H-FHR, respectively, and Figures 4 (b) and 4 (d) showcase RP1 and RP2 of a D-FHR, respectively. Patterns present in Figures 4 (a) and (c) diff from the patterns present in Figures 4 (b) and 4 (d). For instance, the pattern showing up at the coordinates (300, 300) till (500, 500) time units in Figures 4 (b) and 4 (d) differs from that present in Figures 4 (a) and 4 (c). Moreover, the pattern show up at the coordinates (1, 1) till (100, 100) time units in Figures 4 (b) and 4 (d) does not exist in Figures 4 (a) and 4 (c). The former and the latter pattern findings are mean of reflecting the difference between the two FHRs.Figure 5 showcases the three simulated URPs. Figure 5 (a) represents 3-d embedded recurrence plot with specific settings RP3 of H-FHR, (b) the 3-d embedded recurrence plot with specific settings RP3 of D-FHR, (c) the derivative-based recurrence plot RP4 of the H-FHR, (d) the derivative-based recurrence plot RP4 of the D-FHR, (e) The m-time pattern recurrence plot RP5 of the H-FHR and (f) the m-time pattern recurrence plot RP5 of the D-FHR. Note that the mean diagonal length is higher in case of the distressed fetus, and the length of identity (LOI) i.e. the main diagonal line in the RP is more dense in case of the distressed fetus. This suggests that the cardiac activity of the distressed fetus is more predictable than that of the healthy one. A greater predictability is possible when a loss in complexity of the heart system appears [10]. The previous fact could be triggered by the fragile interaction between brain and heart of the fetus caused by hypoxia.
RQA sensitivity, specificity, precision and accuracy of discrimination: Figure 6 sets out the five recurrence quantification parameters computed from the recurrence plots described in section 2. Figure 6 (a) shows the average of DET(%) as a function of the unembedded RP, embedded RP in 3-d, embedded RP with specific settings, derivative- based RP and 2-time pattern RP, RP1, RP2, RP3, RP4 and RP5, respectively. Figure 6 (b) represents the average CDET(%) relative to the five techniques. Figure 6 (c) shows the average
Figure 6: The recurrence quantification analysis (RQA) relative to the standard and unbiased Recurrence. Plots of healthy and distressed FHRs shown in gray and orange colors, respectively. (a) The mean DET(%) as a function of the unembedded RP, embedded RP in 3-d, embedded RP with specific settings, derivative-based RP and 2-time pattern RP, RP1, RP2, RP3, RP4 and RP5, receptively. (b) The mean CDET (%) relative of the five RP techniques. (c) The average Percentage Reduced Sojourn Points (PRSP(%)) as a function of the five Recurrence Plots (RPs). (d) The average mean RR (%) as a function of the five RPs. (e) The mean En (%) as a function of the five RPs.
PRSP(%) as a function of the five RPs. Figure 6 (d) represents the average RR(%) as a function of the five RPs. Finally, Figure 6 (e) shows the average En(%) as a function of the standard and unbiased RPs. The gray color corresponds to the H-FHR and the orange color corresponds to the D-FHR, REs in percentage were reported between two diff t bar graphs. Blue and red SDs were imposed on top of the bar graphs of H-FHRs and D-FHRs, respectively.
Entropy bar plots in Figure 6 (e) shows that H-FHRs are more irregular (-65%) compared to D-FHRs (-55%). This finding is in accordance with the fact that some diseases turn the FHR to be more regular than in its healthy behaviour [3,10].
Statistical measures including the sensitivity, specificity, precision and accuracy of discrimination were computed (Table 2).
| ED RQA | Sensitivity | Specificity | Precision | Accuracy | Discriminative Power κ score(%) |
|---|---|---|---|---|---|
| DET | 80% | 20% | 50% | 50% | 0.0% |
| CDET* | 80% | 100% | 100% | 90% | 80% |
| PRSP | 20% | 80% | 50% | 50% | 0.0% |
| RR* | 80% | 100% | 100% | 90% | 86.5% |
| En* | 80% | 100% | 100% | 90% | 86.5% |
Table 2: The Effectiveness of Discrimination (ED) of Fetal Heart Rates (FHRs) by the sensitivity,specificity, precision and accuracy measures in percentages of the Recurrence Quantification Analysis (RQA).
Table 2 reports the Effectiveness of Discrimination (ED) of FHRs by both the sensitivity and specificity measures in percentages of the Recurrence Quantification Analysis (RQA), in addition to the accuracy and precision values. Table 2 reveals that the utmost sensitivity and specificity belong to CDET descriptor as it was proposed in our previous paper [2]. Moreover, both the precision and accuracy were computed in this paper, and the best precision and accuracy corresponded to CDET descriptor followed by RR and En. The latter parameters are associated an asterisk in Table 2 to highlight their significance.
Of all the five RQAs, the sensitivity of the discrimination between healthy and IUGR FHRs is arranged as follows: Sensitivity(DET)=Sensi tivity(En)>Sensitivity(PRSP ), however the specificity of discrimination is as follows: Specificity(En)>Specificity(PRSP)>Specificity(DET ).
Discriminative power: As Cohen’s kappa coefficient (κ score) measures the degree of consistency between data- sets [35], it was calculated from the RQAs of the FHRs datasets. Table 2 reports the κ scores or the discriminative powers in percentages. According to Landis et al. [33], RR, En and CDET of the FHR database is perfectly consistent as κ=86.5% for RR and En and κ=80.0% for %CDET. Therefore, their discriminative power is high, unlike DET and PRSP where the consistency of discrimination is slight and thus the power is slight too.
Relative separation/error and standard deviation: Provided the statistical measures including the sensitivity, specificity, precision, accuracy and the discriminative power, the absolute Relative Error (RE) and SD were manipulated by Eqs. 7 and 8 and the results are reported in Table 3 (Table 3).
| Measurements RQA | RE (H-FHR, IUGR-FHR) | SD (H-FHR, IUGR-FHR) |
|---|---|---|
| DET | 11.72 | ±0.07 |
| CDET* | 42.60 | ±0.12 |
| PRSP | 11.62 | ±13.40 |
| RR | 11.00 | ±0.02 |
| En | 13.33 | ±11.15 |
Table 3: The statistical measurements, mean relative error (RE) and standard deviations (SDs) between the H-FHRs and IUGR-FHRs using the recurrence quantification parameters.
High values were shown in bold in Table 3 and the asterisk was associated the best mean  and
and 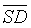 couple. Table 3 shows the negligible
couple. Table 3 shows the negligible 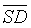 values for DET, CDET and RR classification indicators. Moreover, it shows the significant values of
values for DET, CDET and RR classification indicators. Moreover, it shows the significant values of 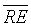 using CDET followed by En, DET and then RR. Thus according to the latter statistical results, the appropriate indicator of IUGR i.e. the best parameter that achieves the discrimination between H-FHRs and IUGR-FHRs is the CDET parameter. The ED based on the
using CDET followed by En, DET and then RR. Thus according to the latter statistical results, the appropriate indicator of IUGR i.e. the best parameter that achieves the discrimination between H-FHRs and IUGR-FHRs is the CDET parameter. The ED based on the 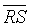 values in Table 2 are arranged in the following descending order of classification importance: CDET>En>DET>PRSP>RR. However, the ED based on the
values in Table 2 are arranged in the following descending order of classification importance: CDET>En>DET>PRSP>RR. However, the ED based on the 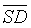 s are arranged in the following descending order of importance: RR>DET>CDET>En>PRSP.
s are arranged in the following descending order of importance: RR>DET>CDET>En>PRSP.
The CDET parameter has yielded the maximum 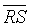 between the two FHR classes, a minimum SD and it possessed a high sensitivity and specificity values with 100% precision and 90% accuracy of diagnosis and classification.
between the two FHR classes, a minimum SD and it possessed a high sensitivity and specificity values with 100% precision and 90% accuracy of diagnosis and classification.
Although most of the values of 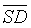 (RR) and
(RR) and 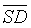 (DET) parameters were comparable to those obtained by CDET, and both the sensitivity and specificity of discrimination of RR were the same as that of CDET, the specificity of DET was 80% less than the specificity of CDET (see Table 2). Thereby, RR parameter is more likely adapted for discrimination than DET parameter. Besides,
(DET) parameters were comparable to those obtained by CDET, and both the sensitivity and specificity of discrimination of RR were the same as that of CDET, the specificity of DET was 80% less than the specificity of CDET (see Table 2). Thereby, RR parameter is more likely adapted for discrimination than DET parameter. Besides, 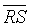 values that both RR and DET have yielded were two to three times less than that produced by CDET, still they served as moderate generic markers for intrauterine growth restricted fetuses (see Table 3). Therefore, RR and DET parameters are both less effective than CDET.
values that both RR and DET have yielded were two to three times less than that produced by CDET, still they served as moderate generic markers for intrauterine growth restricted fetuses (see Table 3). Therefore, RR and DET parameters are both less effective than CDET.
The non-negligible values of the 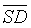 (En) and
(En) and 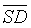 (PRSPs) (see Table 3) reveal that these two indicators are sensitive to the fluctuations of data, thus they might be useful in the extraction of other types of complexities. However, the RQA parameters revealing the highest
(PRSPs) (see Table 3) reveal that these two indicators are sensitive to the fluctuations of data, thus they might be useful in the extraction of other types of complexities. However, the RQA parameters revealing the highest 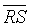 values and the lowest
values and the lowest 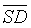 values are the utmost parameters to discrimination healthy from distressed FHR cases. The latter information was fulfilled by the use of the CDET quantification parameter.
values are the utmost parameters to discrimination healthy from distressed FHR cases. The latter information was fulfilled by the use of the CDET quantification parameter.
Of all the 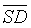 (RQA) values,
(RQA) values, 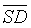 (PRSP) was the highest and
(PRSP) was the highest and 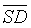 (DET) the lowest, thereby, DET data are less dispersed. Moreover, while comparing PRSP to DET we noticed that the sensitivity was 60% higher for DET than for PRSP, however the specificity was 60% lower for PRSPs than for DET. However, the accuracy and the precision were similar 50%. Of all RQA, CDET followed by RR were the utmost parameters to discriminate healthy from Intrauterine Growth Restricted fetuses. In addition, CDET served as the ultimate generic marker for fetal distress caused by IUGR.
(DET) the lowest, thereby, DET data are less dispersed. Moreover, while comparing PRSP to DET we noticed that the sensitivity was 60% higher for DET than for PRSP, however the specificity was 60% lower for PRSPs than for DET. However, the accuracy and the precision were similar 50%. Of all RQA, CDET followed by RR were the utmost parameters to discriminate healthy from Intrauterine Growth Restricted fetuses. In addition, CDET served as the ultimate generic marker for fetal distress caused by IUGR.
Although RR quantitative parameter values were in general small (Figure 6 (d)), a higher RR parameter characterized H-FHRs compared to RR of D-FHRs. Moreover, H-FHRs were more irregular than D-FHRs (Figure 6 (e)). The former result still emphasizes the fact that healthy biomedical signals, i.e. H-FHRs, are highly complex in nature [36].
Unlike the previous work [3], this paper enriches FHR analysis by detecting IUGR fetuses from the used FHR dataset, it showcases also a sample of URPs and RPs of one (healthy, IUGR)-FHR couple out of the 50 studied FHRs. Nevertheless the information inferred from these plots are not suffit, we showed that the quantitative results of RQA followed by the statistical measurements support the qualitative results in Figures 5 and 6.
Discrimination of FHRs was not possible when the classical obstetrical parameters were used, like accelerations1 which were surprisingly more visible in case of distressed fetuses
1FHR acceleration is an increase of the heart beats by at least 15 bmp during at least 15 seconds. This is the classical parameter with the smallest false positive rate in detecting hypoxia than healthy fetuses [10]. 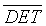 remained greater for healthy fetuses compared to distressed fetuses. The behavior of H-FHRs reported in this work was in accordance with the results reported in [3,4,9].
remained greater for healthy fetuses compared to distressed fetuses. The behavior of H-FHRs reported in this work was in accordance with the results reported in [3,4,9].
Of all the RP techniques, the derivative-based RP (RP4) is the least RP contaminated with sojourn points (the cleanest RP) followed by 2-time pattern RP (RP5) and RP with specific settings (RP3), then the standard embedded RP [18] (RP2) and finally the standard unembedded RP [31] (RP1) (see Figures 6 (b) and 6 (c)). The former result is in accordance with the alternative works that experienced the presence of sojourn points and the bias of RP1 [2,31].
One of the limitations of the application of RP5 to FHRs is the choice of a pattern of m=2 and the computation of RQA merely from the 2-time pattern recurrence plot. By analogy to standard embedding RPs and as it was inferred that CDET increases when d is increased, we anticipate that the performance of discrimination of RP5 and its corresponding RQA’s for (m>2) could surpass the alternative unbiased RPs [3]. However, the latter idea should be investigated.
Moreover, by means of RP4 it was possible to classify healthy from IUGR-fetuses from their heart rate recordings. Although the difference was not huge, yet it still showcases the advantage of the unbiased RP4 based on the discrimination related to differences in the RQA parameters between H-FHRs and D-FHRs [37-40].
The FHR complexity analysis findings of this work are in accordance with the physiological information [7,10], DET remained greater for healthy fetuses compared to IUGR-fetuses, the rationale is the complexity degradation of the heart rate in IUGR-fetuses compared to healthy fetuses. A great predictability of D-FHRs is foreseen when the complexity of the fetal heart is degraded. This complexity degradation can be due to a lower interaction between the brain and the heart of the fetus as a result of hypoxia, the drop off in the concentration of oxygen in the fetal bloodstream [10].
The evaluation of the power of discrimination is carried out using Cohen’s kappa coefficient from the unbiased recurrence quantification analysis, and is compared to standard recurrence plots. Experimental results showed that the cross-determinism parameter (extracted from Unbiased Recurrence Plots URPs) is the utmost parameter providing a high discriminative power (86.5%), the maximum relative separation between the two fetal heart rate sets (42.6%), and minimum standard deviation (± 0.12%).
Both RR and DET parameters served as moderate markers of intrauterine growth restricted (IUGR) fetuses, while the novel CDET parameter served as the ultimate generic marker to discriminate healthy from IUGR-fetal heart rate. This research should be extended to link certain diseases to the detected complexities and IUGR.
The diagnosis of IUGR-fetal heart rates by the URPs and their corresponding unbiased Recurrence Quantification Analysis (RQAs) is improved in this work as compared to two standard RP techniques and their corresponding RQAs. These findings open the door for advanced machines and advanced detection of distress to decide for immediate and preterm deliveries.
The authors would like to thank the National Council for Scientific Research in Lebanon (CNRS-L), the Lebanese University and Imaging and Brain Laboratory and the National Institute for Health and Medical Research, INSERM U930 in Tours (France) for financially supporting this work. The authors are also grateful to Prof. F. Perrotin and his team in the Obstetric Department at CHRU-Bretonneau Hospital of Tours for the FHR database, and are grateful to Miss Faten Khatib from the Sharp Chula Vista Medical Center in the U.S. for her valuable feedback.