Journal of Geology & Geophysics

Journal of Geology & Geophysics
Open Access

ISSN: 2381-8719

+44 1478 350008

Research Article - (2012) Volume 1, Issue 1

View PDF Download PDF

A New Method to Predict Ratio of Width to Height Rock Pillar in Twin Circular Tunnels

Asghar Siahmansouri1*, Javad Gholamnejad2 and Mohammad Fatehi Marji3
1M.Sc. Student, Department of Mining and Metallurgical Engineering, Yazd University, Yazd, Iran
2Associate Professor, Department of Mining and Metallurgical Engineering, Yazd University, Yazd, Iran
3Associate Professor, Department of Mining and Metallurgical Engineering, Yazd University, Yazd, Iran
*Corresponding Author: Asghar Siahmansouri, M.Sc. student, Department of Mining and Metallurgical Engineering, Yazd University, Yazd, Iran Email:

Abstract

Twin tunnels can be used for many applications. Interaction between two tunnels is an important problem in tunnel engineering that should be studied specially. Numerical investigations are well adapted to field data and numerical methods can be used in design of rock pillar of twin circular tunnels. So far no relationship has been provided to estimate the minimum stable rock pillar. In this paper the interaction between twin circular tunnels has been studied using 2D finite element analysis. To do this, a great number of twin tunnels were modeled in Phase2 software with different conditions of rock mass (RMR value) and depth of tunnel. Models were analyzed and minimum stable rock pillar was determined. This process was repeated for three different ratios of K (ratio of horizontal stress to vertical stress, 0.5, 1 and 1.5). Finally, according to the linear and nonlinear regression methods, the best merit function was fitted to result of numerical analysis. Then, a new approximate formula was proposed to predict ratio of width to height rock pillar according to RMR value and depth of twin circular tunnels with different K values. The formulae are very accurate (coefficient of correlation equals to 0.96) that can be used for predicting ratio of width to height rock pillar in twin circular tunnels.

Keywords: Twin circular tunnels, Rock pillar, Numerical modeling, Non linear regression, Phase2

Introduction

Nowadays, multiple excavations can be used for many applications such as: roads, railways, subways, hydraulic tunnels, etc. Of these, the twin tunnels are used more than other spaces. Interaction between these tunnels is an important problem in tunnel engineering that should be studied specially.

Multiple excavations have been studied in models and results are presented by Obert and Duvall [1,2]. Under elastic conditions, two tunnels interact with each other if separated by a thickness of rock less than two times the sum of their dimensions in the direction parallel to the separation. As tunnels approach each other, the average stress in the rock pillar between them increases and approaches the maximum tangential stress (Figure 1).

As a greater number of discontinuities are contained within a sample of rock, its strength must decrease. Accordingly, when the span of a tunnel is many times greater than the average spacing between excavations, the tunnel cannot be expected to stand without artificial support [3].

Stress concentrations will generally be the least troublesome if smooth shapes are used, without corners and reentrants, and if the major axis is aligned to the major principal stress, with the ratio of width to height proportional to K (horizontal stress to vertical stress ratio) [4]. Openings of other shapes have been solved mathematically and solutions can be found in Muskhelishvili [5]. Elliptical and other idealized shapes are discussed by Jaeger and Cook and Obert and Duvall [1,6].

For twin tunnels, by decrease in tunnels spacing, the total project cost would decrease; using geotechnical studies, preparation and cross cut can be reduced. On the other hand, when the spacing between tunnels is very little, plastic zones of the tunnels would join each other; therefore rock pillar placed in plastic zone and tunnels may become unstable. So, the minimum stable rock pillar between twin tunnels should be determined by technical and economic studies. To do this, the spacing between two tunnels should be far enough to prevent plastic zones from meeting.

Stresses around multi-excavations are determined using modeling and numerical methods [7]. A numerical investigation of rock pillar failure mechanism in underground openings was done by Mortazavi et al. [8]. They found that numerical investigations are well adapted to the field data and numerical methods can be used in the design of rock pillars in underground structures [8]. In this paper, the interaction between two tunnels has been studied using 2D finite element analysis. To do this, at first the stress concentrations of twin tunnels was investigated. Then, a great number of twin tunnels were modeled in Phase2 software with different conditions of rock mass and depth of tunnels for three different ratios of K (0.5, 1 and 1.5). Models were analyzed and minimum stable rock pillar was determined. Finally, according to the linear and nonlinear regression methods, the best merit function was fitted to these data. Then, a new approximate formula for predicting ratio of width to height rock pillar in twin circular tunnels was proposed. The formula is very accurate with high correlation coefficient (0.96) that can be used for predicting ratio of width to height rock pillar in twin circular tunnels.

Proposed Method

In rock stressed below its elastic limit, that is, below about one-half of the compressive strength, and in which joints are widely spaced and tightly pre-compressed or healed, it is often acceptable to consider an opening as a long hole of constant cross section in an infinite volume. This is the plane strain equivalent of a hole in a plate, and we can use the solution to the problem of a circular hole in a biaxialy loaded plate of homogeneous, isotropic, continuous, linearly elastic material-the Kirsch solution [3].

Geometrical modeling

In this paper a twin circular tunnels was considered in massive rock and depth of H. Geometrical parameters of twin circular tunnels are shown in Figure 1.

geology-geosciences-twin-circular

Figure 1: Geometrical parameters of twin circular tunnels in massive rock I: Ratio of secondary stress to initial stress around circular tunnel I (σθ/γH) II: Ratio of secondary stress to initial stress around circular tunnel II (σθ/γH) III: Interaction of I and II secondary stress on rock pillar between twin circular tunnels (I+II).

The Phase2 software is used for modeling. The Phase2 software in addition to simplicity is sufficiently accurate at modeling complex underground spaces. This software is based on finite element, and modeling is doing as two-dimensional assuming the plane strain [9]. The rock mass is a continuum and the software is a high speed for modeling of many of tunnel; so the software was chosen for stability analysis of the twin circular tunnels [9]. The diameter of each (W) is 10 meters. The boundaries of the model expanded as five times the diameter of the tunnel. Three angular elements are used for mesh generation in the model (Figure 2).

geology-geosciences-circular-tunnels

Figure 2: Modeling of twin circular tunnels in Phase2.

Mechanical modeling

Bieniawski developed his scheme using data obtained mainly from civil engineering excavations in sedimentary rocks in South Africa [10-13]. Bieniawski’s geomechanical classification system provides a general Rock Mass Rating (RMR) increasing with rock quality from 0 to 100. It is based upon five universal parameters: strength of the rock, drill core quality, groundwater conditions, joint and fracture spacing, and joint characteristics. A sixth parameter, orientation of joints, is entered differently for specific application in tunneling, mining, and foundations. Increments of rock mass rating corresponding to each parameter are summed to determine RMR [3,11-13]. RMR can show the quality of rock mass, as well. According to the RMR value, rocks are divided into 13 groups (mat 1 to mat 13). Geomechanical prosperities of rock groups are given in table 1.

Mat. RMR UCS (MPa) Em (GPa) υ γ (MN/m3)
mat 1 90 250 100 0.2 0.027
mat 2 85 225 75 0.209 0.027
mat 3 80 200 56 0.218 0.027
mat 4 75 175 42 0.227 0.027
mat 5 70 150 32 0.236 0.027
mat 6 65 125 24 0.245 0.027
mat 7 60 100 18 0.254 0.027
mat 8 55 75 13 0.263 0.027
mat 9 50 50 10 0.27 0.027
mat 10 45 30 7.5 0.277 0.027
mat 11 40 20 6 0.285 0.027
mat 12 35 10 4.2 0.293 0.027
mat 13 30 5 3.1 0.3 0.027

Table 1: Geomechanical prosperities of rock groups.

Hoek and Brown criterion was used for stability analysis investigation. Hoek and Brown proposed the following criterion for rock masses [14-17].

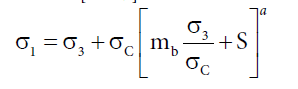image(1)

Studies showed that above criterion is valid for massive rock, if RMR>25 [16]. Geological Strength Index (GSI) is calculated by [16]:

GSI (RMR1989− 5 (RMR1989>23)  (2)

Constant coefficient mb, S and a are determined by:

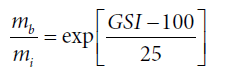image  (3)

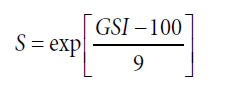image  (4)

a=0.5  (5)

There m i is material constant.

According to the above relations, Hoek and Brown parameters are calculated. These parameters are given in table 2.

Mat. GSI mi mb S
mat 1 85 34 18.7 0.2
mat 2 80 31.5 14.1 0.11
mat 3 75 29 10.7 0.06
mat 4 70 26.5 8 0.035
mat 5 65 24 6 0.02
mat 6 60 21.5 4.4 0.012
mat 7 55 19 3.1 0.007
mat 8 50 16.5 2.3 0.004
mat 9 45 14 1.5 0.0022
mat 10 40 11.5 1 0.0013
mat 11 35 9 0.7 0.0007
mat 12 30 6.5 0.4 0.0004
mat 13 25 4 0.2 0.00025

Table 2: Hoek and Brown prosperities of rock groups.

Stability Analysis

All rock groups were modeled at 5 difference depths (50, 150, 300, 500 and 750 meters). The models were analyzed for different K values (ratio of horizontal stress to vertical stress, K=1, k=0.5 and k=1.5). For each model, the minimum stable rock pillar was determined using try and error. For this purpose, the plastic zones of the tunnels should be separated. Rock is placed in plastic zone if safety factor value is less than 1.5. For instance, safety factor contour value of rock group 4 is shown in Figure 3.

geology-geosciences-Safety-factor

Figure 3: Safety factor contour value of rock group 4 at depth of 750 m (K=1) in Phase2.

Stability analysis of K=1

The results of stability analysis are given in table 3, for K ratio equal to 1.

Mat. RMR H (m) P (m) F Mat. RMR H (m) P (m) F
mat 1 90 50 1 0.1 mat 7 70 500 6.4(10) 0.54
mat 1 90 150 2.1 0.21 mat 7 70 750 7.2(10) 0.55
mat 1 90 300 3.1 0.31 mat 8 65 50 4.2(10) 0.31
mat 1 90 500 3.8 0.38 mat 8 65 150 5.4(10) 0.44
mat 1 90 750 4.3 0.43 mat 8 65 300 6.4(10) 0.52
mat 2 85 50 1.2 0.12 mat 8 65 500 7.4(10) 0.55
mat 2 85 150 2.7 0.27 mat 8 65 750 8.4(10) 0.58
mat 2 85 300 3.8 0.38 mat 9 50 50 5(10) 0.39
mat 2 85 500 4.3 0.43 mat 9 50 150 6.4(10) 0.51
mat 2 85 750 4.7 0.47 mat 9 50 300 8(10) 0.54
mat 3 80 50 1.5 0.15 mat 9 50 500 10(10) 0.57
mat 3 80 150 3.2 0.32 mat 9 50 750 11(10) 0.62
mat 3 80 300 4.1 0.41 mat 10 45 50 5.8 0.43
mat 3 80 500 4.6 0.46 mat 10 45 150 8 0.52
mat 3 80 750 5.2 0.52 mat 10 45 300 10.2 0.56
mat 4 75 50 1.8 0.18 mat 10 45 500 12.2 0.6
mat 4 75 150 3.6 0.36 mat 10 45 750 13.6 0.68
mat 4 75 300 4.4 0.44 mat 11 40 50 7 0.44
mat 4 75 500 5.2 0.52 mat 11 40 150 10.2 0.55
mat 4 75 750 5.5 0.55 mat 11 40 300 12.8 0.59
mat 5 70 50 2.6 0.26 mat 11 40 500 15.2 0.65
mat 5 70 150 4.2 0.42 mat 11 40 750 17.8 0.7
mat 5 70 300 5.2 0.52 mat 12 35 50 9.8 0.48
mat 5 70 500 5.6 0.56 mat 12 35 150 14.6 0.57
mat 5 70 750 6 0.6 mat 12 35 300 18.4 0.64
mat 6 65 50 3.4 0.34 mat 12 35 500 22.2 0.71
mat 6 65 150 4.6 0.46 mat 12 35 750 25.2 0.78
mat 6 65 300 5.4 0.54 mat 13 30 50 15 0.565
mat 6 65 500 6 0.6 mat 13 30 150 22.4 0.4
mat 6 65 750 6.6 0.66 mat 13 30 300 27.2 0.327
mat 7 70 50 4 0.4 mat 13 30 500 32 0.278
mat 7 70 150 5.2 0.52 mat 13 30 750 36.6 0.241
mat 7 70 300 6 0.6          
* F is ratio of minimum rock pillar width (P) to tunnel height (W). (Figure 1)

Table 3: Calculated coefficient of pillar for the different RMR and depth. (K=1).

Stability Analysis of K=0.5

The results of stability analysis are given in table 4, for K ratio equal to 0.5.

Mat. RMR H (m) P (m) F Mat. RMR H (m) P (m) F
mat 1 90 50 1 0.1 mat 6 65 50 2.8 0.28
mat 1 90 150 1.6 0.16 mat 6 65 150 4 0.4
mat 1 90 300 2.4 0.24 mat 6 65 300 5 0.5
mat 1 90 500 3 0.3 mat 6 65 500 5.8 0.58
mat 1 90 750 3.6 0.36 mat 6 65 750 6.6 0.66
mat 2 85 50 1.2 0.12 mat 7 70 50 3.6 0.36
mat 2 85 150 2 0.2 mat 7 70 150 5 0.5
mat 2 85 300 3 0.3 mat 7 70 300 5.8 0.58
mat 2 85 500 3.4 0.34 mat 7 70 500 3.6 0.36
mat 2 85 750 4 0.4 mat 7 70 750 5 0.5
mat 3 80 50 1.4 0.14 mat 8 65 50 3.6() 0.36
mat 3 80 150 2.6 0.26 mat 8 65 150 5() 0.5
mat 3 80 300 3.4 0.34 mat 8 65 300 6.4() 0.64
mat 3 80 500 4 0.4 mat 8 65 500 8() 0.8
mat 3 80 750 4.4 0.44 mat 8 65 750 10() 1
mat 4 75 50 2.2 0.22 mat 9 50 50 4.4() 0.44
mat 4 75 150 3.2 0.32 mat 9 50 150 6.4() 0.64
mat 4 75 300 3.8 0.38 mat 9 50 300 10() 1
mat 4 75 500 4.4 0.44 mat 9 50 500 12() 1.2
mat 4 75 750 5 0.5 mat 9 50 750 17() 1.7
mat 5 70 50 2.2 0.22 mat 10 45 50 5.8() 0.58
mat 5 70 150 3.6 0.36 mat 10 45 150 11() 1.1
mat 5 70 300 4.4 0.44 mat 11 40 50 7.8() 0.78
mat 5 70 500 5.2 0.52 mat 11 40 150 15.6() 1.56
mat 5 70 750 5.6 0.56          

Table 4: Calculated coefficient of pillar for the different RMR and depth. (K=0.5).

Stability Analysis of K=1.5

The results of stability analysis are given in table 5, for K ratio equal to 1.5.

Mat. RMR H (m) P (m) F Mat. RMR H (m) P (m) F
mat 1 90 50 1 0.1 mat 6 65 300 6 0.6
mat 1 90 150 2 0.2 mat 6 65 500 6.6 0.66
mat 1 90 300 3.1 0.31 mat 6 65 750 7 0.7
mat 1 90 500 4.2 0.42 mat 7 70 50 4.4 0.44
mat 1 90 750 4.6 0.46 mat 7 70 150 5.8 0.58
mat 2 85 50 1.2 0.12 mat 7 70 300 6.6 0.66
mat 2 85 150 2.7 0.27 mat 7 70 500 7 0.7
mat 2 85 300 4 0.4 mat 7 70 750 7.6 0.76
mat 2 85 500 4.8 0.48 mat 8 65 50 4.6() 0.46
mat 2 85 750 5.4 0.54 mat 8 65 150 5.8() 0.58
mat 3 80 50 1.5 0.15 mat 8 65 300 6.8() 0.68
mat 3 80 150 3.4 0.34 mat 8 65 500 7.4() 0.74
mat 3 80 300 4.8 0.48 mat 8 65 750 8() 0.8
mat 3 80 500 5.4 0.54 mat 9 50 50 5.4() 0.54
mat 3 80 750 6 0.6 mat 9 50 150 6.6() 0.66
mat 4 75 50 2 0.2 mat 9 50 300 7.8() 0.78
mat 4 75 150 4.2 0.42 mat 9 50 500 8.6() 0.86
mat 4 75 300 5.2 0.52 mat 9 50 750 9.6() 0.96
mat 4 75 500 5.8 0.58 mat 10 45 50 6() 0.6
mat 4 75 750 6.2 0.62 mat 10 45 150 8() 0.8
mat 5 70 50 2.8 0.28 mat 10 45 300 9.4() 0.94
mat 5 70 150 4.8 0.48 mat 10 45 500 11() 1.1
mat 5 70 300 5.6 0.56 mat 10 45 750 12.2() 1.22
mat 5 70 500 6.2 0.62 mat 11 40 50 7() 0.7
mat 5 70 750 6.4 0.64 mat 11 40 150 9.4() 0.94
mat 6 65 50 3.8 0.38 mat 11 40 300 11.4() 1.14
mat 6 65 150 5.4 0.54          

Table 5: Calculated coefficient of pillar for the different RMR and depth. (K=1.5).

In condition of non-hydrostatic (K=0.5 and K=1.5), weak rock mass (RMR<50) do not tolerate difference of vertical and horizontal stress; in this condition, the depth is more and rock is weaker, K is limited to 1. In non-hydrostatic conditions, number of data is less than hydrostatic condition.

Results and Discussions

Regression analysis gives us the ability to summarize a collection of sampled data and fitting to a model that will accurately describe the data. Regression analysis can turn the sampled data points into a smooth continuous function. This measurement of agreement is called the merit function. There are two widely used and accepted methods for performing regression analysis. The first, and easiest to implement, is linear regression. The second more general method is called nonlinear regression. In this paper both linear and nonlinear approach has been used for the analysis [18,19].

According to the linear and nonlinear regression methods, a lot of functions are fitted to all data, and then the best merit function can be chosen. These functions must be comprehensive and have high correlation coefficients. Also, merit function should be simple so that, geotechnical engineers can use it in the site easily. These models contain two independent variables, RMR and H, three constant parameters, a, b and c, and the dependent variable, F, estimated based on the independent variables and constants. Results of analysis and merit functions are investigated for difference K ratio.

Three-dimensional graph of merit function is shown in Figure 4.

geology-geosciences-curve-fitting

Figure 4: Regression method, curve fitting to all data (167#) for K=0.5, K=1, K=1.5, correlation coefficient, R2=0.96.

The merit function for the graph shown in Figure 3 can be estimated as:

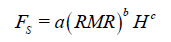image  (6)

Where, FS is coefficient of pillar, for the best fitted function constant factors are shown in Table 6.

Constant factors
a 370
b -2
c 0.33

Table 6: Constant factors of Eq. 6.

Then coefficient of pillar, FS can be written as:

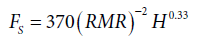image  (7)

This is a very accurate formula with correlation coefficient, R2=0.96.

Conclusion

In this paper the interaction between twin circular tunnels has been studied using 2D finite element analysis. For this purpose, a great number of twin tunnels were modeled in Phase2 software with different conditions of rock mass (RMR value), depth of tunnels and three different ratios of K (ratio of horizontal stress to vertical stress, 0.5, 1 and 1.5). Finally, according to the nonlinear regression methods, the best function was fitted to result of numerical analysis of twin tunnels. Then, a new approximate formula for estimating the minimum rock pillar according to RMR value and depth of twin circular tunnels was proposed for different K. The formula is very accurate with high correlation coefficient (0.96) that can be used for estimating the minimum rock pillar of twin circular tunnels.

References

  1. Obert L, Duvall WI (1967) Rock mechanics and the design of structures in rocks. Wiley, New York.
  2. Obert L, Duvall WI, Merrill RH (1960) Design of underground opening in competent rock. USBM Bull.
  3. Goodman RE (1989) Introduction to rock mechanics. (2ndedn), John Wiley & Sons, Toronto.
  4. Duvall WI (1976) General principles of underground opening design in competent rock. The 17th US Symposium on Rock Mechanics (USRMS).
  5. Muskhelishvili NI (1953) Some basic problems of the mathematical theory of elasticity. (4thedn), translated by Radok JRM.
  6. Jaeger JC, Cook NGW (1979) Fundamentals of rock mechanics. (3rdedn), Chapman & Hall, London.
  7. Vutukuri VS, Katsuyama K (1994) Introduction to rock mechanics. Industrial Publishing & Consulting Inc., Tokyo.
  8. Mortazavi A, Hassani FP, Shabani M (2009) A numerical investigation of rock pillar failure mechanism in underground openings. Computers and Geotechnics 36: 691-697.
  9. Brady BHG, Brown ET (1985) Rock mechanics for underground mining. George Allen & Unwin, London.
  10. Bieniawski ZT (1974) Geomechanics classification of rock masses and its application in tunneling. Proc. 3rd Congress on Rock Mechanics, ISRM, Denver.
  11. Bieniawski ZT (1976) Rock mass classifications in rock engineering. Proceedings of Symposium on Exploration for Rock Engineering, Balkema, Rotterdam 1: 97-106.
  12. Bieniawski ZT (1989) Engineering rock mass classifications: a complete manual for engineers and geologists in mining, civil, and petroleum engineering. John Wiley & Sons, NewYork.
  13. Hoek E, Brown ET (1980) Empirical strength criterion for rock masses. Journal of Geotechnical and Geoenvironmental Engineering 106: 1013-1035.
  14. Hoek E, Brown ET (1988) The Hoek-Brown failure criterion – a 1988 update. Proceedings of the 15th Canadian Rock Mechanics Symposium. Symp, University of Toronto, Ontario, 31-38.
  15. Hoek E, Wood D, Shah S (1992) A modified Hoek-Brown criterion for jointed rock masses. Proc. Rock Characterization, Symp. Int. Sock. Rock, 209-214.
  16. Hoek E, Kaiser PK, Bawden WF (1995) Support of underground excavations in hard rock. Rotterdam, Balkema.
  17. Draper NR, Smith H (1981) Applied Regression Analysis. Second edition, John Wiley & Sons, USA.
  18. Ratkowsky DA (1990) Handbook of nonlinear regression models. Marcel Dekker, New York.
Citation: Siahmansouri A, Gholamnejad J, Marji MF (2012) A New Method to Predict Ratio of Width to Height Rock Pillar in Twin Circular Tunnels. J Geol Geosci 1:103.

Copyright: © 2012 Siahmansouri A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Top