We found that such locations are correlated to the vulnerable plaque phenotype, which is prone to rupture [7]. Our results demonstrate that at locations of high particle concentration, blood particles change the shear stress distribution and magnitude. Therefore, the non-Newtonian blood flow assumption provides new insights in the characterisation of plaque built up. These results are combined to in-vitro experiments that suggest the influence of blood particles in the activity of cytokines. An unbalance in pro and anti-inflammatory cytokines has been associated to an increase in inflammation [3] and, consequently, in the volume of plaques forming. We anticipate our work to be a starting point for a more sophisticated multi-scale model, which combines experimental findings and computational modelling to characterize arterial segments affected by atherosclerosis. Such model includes a coupling between the distending arterial wall and the non-Newtonian blood flow. Cardiovascular diseases are the leading cause of human death and disability in the world, responsible for an estimated of 17.5 million deaths in 2012, which accounted for 31% of the total global human mortality [8,9]. Indeed, the figures are increasing according to the 2015 updating reports [9,10]. The main contributor to this high mortality is atherosclerosis. Atherosclerosis is a lipid-centred, chronic inflammatory disease which involves plaque formation, and through plaque rupture leads to heart attack, stroke, gangrene and loss of function in the extremities [8-10]. The initiation and progression of atherosclerosis has been linked to disrupted blood flow patterns that occur at bifurcations, curved vessel segments and side-branching locations in the arterial system [11-13]. The shear stress exerted by the flow of blood on the inner lining of arteries (endothelium) is believed to play a crucial role in initiating, and progressing atherosclerosis [13-16]. Lower-than-physiological shear stress values with our without oscillations are considered particularly atherogenic as it induces endothelial dysfunction which leads to plaque deposition [1,14-22]. Numerous mechanisms that contribute to plaque progression have been unveiled but the underlying cellular and molecular processes are not fully understood [1-14]. Endothelial cell apoptosis enhances the arterial wall permeability which results in fatty material accumulation in the arterial wall and the unbalance in pro and antiinflammatory cytokines yields increasing inflammation. Experimental and computational models of atherosclerosis are used to characterize mechanisms involved in plaque initiation and development [20,23,24]. However, both experimental and computational models have limitations - precise or high resolution measurements are not always possible and the technology necessary to obtain detailed fully-coupled computational results are rarely available. The mathematical design and the computational implementation of such models are a challenge. It is important to understand these limitations and to evaluate the relevance of some assumptions when translating conclusions made using a certain environment (e.g., animal model or computational) into clinical applications (in humans), in order to consistently progress towards improving current treatments. In this sense, we anticipate our work to be a starting point for a more sophisticated multi-scale approach, which combines experimental findings and computational modelling to characterize arterial segments affected by atherosclerosis. Until now, the computational modelling carried out to understand the effect of shear stress in the development of atherosclerosis considered the blood a Newtonian fluid, effectively neglecting the blood cells which account for up to 45% of the blood volume and possess non-Newtonian properties [25]. In this study we model blood as a non-Newtonian fluid, taking into account the interactions in between blood cells and between the blood cells and the arterial vessel wall. We infer that the non-Newtonian blood flow assumption provides new insights in the computational characterisation of plaque build-up, as blood particles might change the flow characteristics and the resulting shear forces sensed by the endothelium. Therefore, improving the characterisation of the biophysical environment by using models that more realistically approximate shear stress at locations of plaque deposition is crucial in offering a more accurate and detailed understanding into the mechanism of the atherosclerosis initiation and development. Additionally, this advanced understanding of the disease process could lead to more efficient clinical prevention and treatment of cardiovascular diseases in patients. Our main focus lies on computational models that can be used to support clinical applications. Atherosclerosis is a complex disease related to diverse physiological mechanisms. Indeed, prior research suggests that the Krüppel-like factors (KLFs) family regulates inflammation by affecting the expression of cytokines [26,27].

Computational Methodology

The non-Newtonian blood flow is here modelled using a multiphase technique [23,28-31]. The continuous phase (the plasma) is assumed to be incompressible and Newtonian. This is described through the Navier-Stokes equations, as shown in Equations 1 and 2.

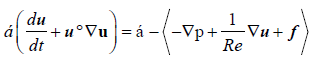(1)

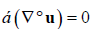(2)

The terms α, f, p, t and Re represent the fluid volume fraction, the source terms, the hydrostatic pressure, the time and the Reynolds number, respectively. The term u is the fluid velocity component, which read u_x, u_y or u_z according to the direction of reference in Cartesian notation. The Reynolds number is a non-dimensional quantity that defines the balance between the inertial and viscous contributions to flow. The term in the momentum equation is the time derivative, which accounts for the unsteady phenomena, and the terms (u°∇u), 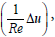and ∇p represent respectively the convective, the diffusive, and the pressure driven flow effects. Incompressibility is achieved by including the constraint (α(∇°u)=0), which stands for the mass conservation equation. The discrete phase - consisting of erythrocytes - is represented by a set of spherical particles, whose behaviour is described by the Newton second law of motion, as shown in Equation 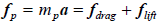3.

(3)

The term f_p represents the forces acting on particles as a function of the inertial mass of the particles (m_p) and the acceleration (α)-- this is the first derivative of the canonical moment. In this study, the force is translated into the drag and the lift forces, f_drag and f_lift, respectively. The constraints related to the artery wall-plasma interaction are described through non-slip boundary conditions. Both the particle-particle and the particle-wall interactions are represented by a variation of the Hooke’s law of elasticity [23,32]. We use a soft-sphere model of collisions (DEM), as previously described [28]. The values of reference to characterise the plasma, the arterial wall, and the erythrocytes were extracted from a previous study [23]. A Poiseuille velocity profile is prescribed at the inlet. At the outlet a convective flow regime was modelled. A pulse wave form is introduced at the inlet to simulate the pumping heart.

Primary cell isolation and culture

Primary porcine aortic endothelial cells (PAECs) were isolated as previously described [33,34] from thoracic aorta segments obtained from approximately 6 month old domestic pigs (Sus scrofa domesticus) and cultured for up to 5 passages at 37°C, saturated humidity and 5% (v/v) CO₂ in DMEM supplemented with 5 mM L-Glutamine, 5 μg/ml EC growth factors, 90 μg/ml heparin and 10% (v/v) foetal calf serum.

EA.hy926 cell culture

Primary human umbilical vein cell line fused with a thioguanineresistant clone of A549 (EA.hy926) by exposure to polyethylene glycol (PEG) was cultured for up to 6 passages at 37°C, saturated humidity and 5% (v/v) CO₂, in 85% DMEM supplemented with 10% FCS, 2.5% L-Glutamine, 1.25% PenStrep, and 1.25% Hepes buffer.

Erythrocytes purification and storage for the multiphase microfluidic experiments

Whole blood was collected in Sodium Heparin. This was transferred to a PBS buffer solution (pH=7.2, 2 mM EDTA) in 50 ml conical tubes. The tubes were centrifuged at 400 g for 20 min, at 4°C, using a swinging bucket rotor without brake; the process was repeated when required until the pellet was fully formed. The erythrocytes were re-suspended in Hanks Balance Salt Solution with glucose at 45% hematocrit, and stored at 4°C.

Electroporation transfection of siKLF2 to down-regulate KLF2

Primary PAECs were electroporated in situ in their adherent state on Indium Tin Oxide coated electrically conductive glass slides using a bespoke electroporation technique [34] with 33 μM siKLF2 solution.

Flow experiments

The above mentioned bespoke electroporation setups were converted into flow channels by mounting bottomless self-adhesive flow chambers (IB-80168) from ibidi GmbH on top of the electroporation wells. A flow setup consisting of the flow channel, a peristaltic pump, platinum-cured silicone tubing, and a bubble catcher media reservoir was used to expose PAECs to physiological 1.5 to 2 Pa shear stress for 24 hours [34]. Images of cell phenotypes were recorded using a Leica DM IL LED-DFC290 phase contrast microscope with the 10X objective.

Microfluidic experiments

Three different sets of EA.hy926-based experiments were carried out, exposing cells to 0.5 to 1.0 Pa shear stress: (1) for 24 hours at 37°C saturated humidity and 5% (v/v) CO2, without erythrocyte addition, (2) for 6 to 8 hours at room temperature (~20°C) without erythrocyte addition, (3) for 6 to 8 hours at room temperature (~20°C) with erythrocyte addition.

Computational blood flow

Both computational and experimental results suggest that in diseased arteries, the peak of particle concentration was registered at the location of higher constriction. Our computational results demonstrate that at locations of high particle concentration -- Figure 1c -- the blood particles change the velocity distribution and, consequently, the shear stress distribution and magnitude (cf. shear map), Figure 1b. The haematocrit is of about 45% of the cross-sectional area. Comparing the velocity distribution in Figure 1 (top-right) with the results for the single phase flow simulation in Figure 1a, we can appreciate differences in the flow magnitude varying between 5 and 45%. Additionally, the wall shear stress (WSS) is directly correlated with the particle distribution. At blue regions the fluid fraction is low and the particle concentration is high. Therefore, we can appreciate on Figure 1b that flow velocities are lower where particle densities are higher (Figures 1c). The indicated Re number (Figure 1) was determined by physiological values from the literature [35] and in vivo measurements in a mouse carotid artery. We hypothesises that the changes in the wall shear stress (WSS) due to the blood particles are directly related to plaque formation. The WSS correlates with velocity patterns and is sensed by the endothelial cells. As mentioned, these mechanisms contribute to cellular activities involved in plaque built up [1-3,20]. Therefore, at sites of increasing cellular activity due to inflammation the blood particles, the outcomes of atherosclerosis might be affected. Indeed, Figure 2 shows recirculation forming downstream of the stenosis. It is important to observe that due to their density erythrocytes behave as fluidized particles, meaning they follow the plasma stream-lines [28]. Thus, while the flow at large scale and healthy arteries is predominantly convective [23], under disease condition, disturbed flow conditions that induce vortexes and jets, might affect homeostasis. As a matter of fact, the characteristics of the vortex and jet shown on Figure 2 indicate that blood particles might affect near wall phenomena, as suggested by the results shown on Figure 1. Additionally, these particles might interact with both the plaque and the endothelium, influencing atheroma development at the respective location.

Figure 1: Rheological flow in a mouse carotid artery, at Re=58: Crosssectional view of the stream-wise velocity. a) Single-phase flow velocity in m/s; b) multiphase flow velocity in m/s; c) fluid distribution at an arterial crosssection (0-100%).

In vitro assessment of signalling pathways modulated by the blood particles

The focus of this study is on flow and, consequently, on shear stress modulated or affected by the dynamics of blood particles and its effects on cellular functions. Blood particle-altered shear stress may induce numerous physiological changes to cells via different signalling pathways. Therefore, we started our experimental study by assessing the effects of pulsatile flow on cell alignment. We identified differences in endothelial cell alignment resulting from differences in the KLF2 activity due to flow disturbances caused by physiologically relevant pulsatile flow conditions. Figure 3 illustrates the influence of oscillatory shear stress on endothelial cell morphology mediated by KLF2. Fluctuations in the shear stress affect cell alignment, Figures 3b and 3d. This supports the hypothesis derived from the former computational results. Moreover, this observation reinforces the assumption that both the shear distribution and magnitude correlate with the patterns of cellular alignment. Therefore, this indicates that the differences in the flow features due to blood particles as showed in Figures 1 and 2 might have local effects on signalling pathways modulated by the wall shear stress. As a consequence, the distribution of blood particles and their interactions might affect homeostasis. Under disease condition, this might enhance molecular unbalance related to increasing inflammation, at locations of plaque deposition. Then, the cells were subjected to oscillatory shear stress for 24 hours. The cells align indicating that the electroporation procedure does not significantly affect the cells properties. 10X microscope objective was used to record all images. The former evidences drove our attention towards the in vitro assessment of the role of erythrocytes in proinflammatory signalling pathways related to atheroma formation [26,27,36,37]. Indeed, our experimental findings suggest that the flow characteristics modified by the erythrocytes affect the endothelial cells alignment and, consequently, this might affect the expression of cytokines regulated by KLF2. Indeed, Figure 4a shows the static control pattern for cell alignment analysis -- endothelial specific cobblestone morphology. Subsequently, the cells were exposed to single-phase flow for 6, 8, and 24 hours. Since the blood samples were stored at 4°C and endothelial cells incubated at 37°C, flow experiments accommodating both cell types were carried out under a compromise temperature (room temperature, ~20°C) for a period of 6 to 8 hours. Under these conditions both cell types remained viable and the flow experiments could be performed. Phase contrast microscopy images of endothelial cells exposed to shear stress of between 0.5 and 1 Pa for 6 hours at 20°C without blood cells, and resulting flow-alignment patterns are shown in Figure 4b. The blood cells were then introduced and the differences in the endothelial cells alignment assessed (Figure 4c). The above range of shear stress was applied, because this promotes the physiological conditions in which vulnerable plaques occurs, in nature. We appreciate differences in cell alignment due to blood cells. Both the cell shape and the alignment patterns change with the erythrocytes. Indeed, in the two-phase flow experiments (Figure 4c), the cells shape is similar to the cobblestone morphology found in the static control (Figure 4a). This indicates differences in mechanical forces applied by the blood on the endothelium. The former results from the flow laminarization induced by the erythrocytes, which correlates to the computational results described via the Figures 1 and 2. Indeed, the difference between the two-phase flow cells morphology (Figure 4c) and the single-phase ones (Figure 4b) is pronounced. We infer that this difference might cause changes in the activity of cytokines, because this activity is modulated by both the intensity and the distribution of the mechanical forces above mentioned. Indeed, together, prior research in the field [1,19,20] identified cell alignment-driven protein expression. Moreover, comparing Figures 4b and 4c we can appreciate that not only cells align in conformation with the flow recirculation but that the cells morphology varies due to erhytrocytes. It is broadly reported in the literature that the endothelial cells alignment indicates differences in protein expression, via differences in the detection of shear forces that are applied by the blood onto the artery wall [1-3,8]. Therefore, we infer that blood particles modify biomechanical flow condition that affect the shear stress alignment functionality of endothelial cells, and are consequently related to signalling pathways that promote atherosclerotic plaques development. We have carried out 40 sets of experiments on cell alignment under different flow conditions and 100 computational simulations. For the same setup, the achieved results exhibited a high level of similarity, differing from each other in about 2%. Moreover, during model validation [29,30,34], we achieved a high level of accuracy comparing our results with the literature.

Figure 2: Illustration of the axial velocity (m/s) in a mouse carotid artery at different cross-sections, with Re=58: The flow direction is indicated by the arrows. The stream lines are shown down-stream of the stenosis, at the topleft view. The region of recirculation is clearly observed.

Figure 3: Deleting shear stress alignment from primary endothelial cells: a) Cell cultured under static (no flow) condition without KLF2 downregulation. The cell monolayer presents the endothelial specific cobblestone morphology; b) Cells exposed to 15-20 dyne/cm2 shear stress generated by the flow of culture media for 24 hours, without down-regulating KLF2 expression. The cells align following flow patterns resulting from a pulsatile inlet; c) Cells electroporated with siRNA, which targets and down-regulates KLF2 expression. Subsequently, 15-20 dyne/cm2 shear stress generated by a pulsatile flow was applied to the cells for 24 hours. KLF2 down-regulation with siRNA technology deleted the shear stress alignment functionality from the endothelial cells; d) Cells electrophorated with siRNA which does not target any gene in the genome.

Figure 4: EA.hy926 alignment under different flow conditions - bright-field images: a) Control -- Cells cultured under static conditions (no flow) for 6 hours. The cell monolayer presents the endothelial specific cobblestone morphology; b) Cells exposed to 0.5-1.0 Pa shear stress generated by the flow of culture media for 6 hours, without erythrocytes. The cells align following pulsatile flow conditions; c) Two-phase flow experiments (erythrocytes at about 45% haematocrit) in which the cells are exposed to 0.5-1.0 Pa pulsatile shear stress for 6 hours.

In this work, we presented the outcomes of the application of a new computational model of blood-flow in diseased arteries. The findings are supported by initial experimental evidences. We anticipate our work to be a starting point for a more sophisticated multi-scale haemorheological model of atherosclerosis that combines computational simulations and an in vitro feedback system. We infer that the non-Newtonian blood flow assumption provides new insights in the computational characterisation of plaque initiation and builtup [23,29,30]. We have shown that blood particles change the flow characteristics and the resulting shear forces sensed by the endothelium. Our results also indicate that differences in the flow magnitude and distribution can lead to different cellular responses. The activation of different mechanisms can yield various responses that might affect the progression of the disease. Therefore, by employing computational models that more realistically represent the complex multi-phase biophysical environment a higher accuracy understanding of shear stress-driven atherosclerosis development can be achieved. The higher degree of understanding promoted by such a model can unveil crucial mechanisms that are currently unknown. Furthermore, this detailed understanding of plaque formation can be used by medical experts to guide the prevention and treatment of the atherosclerotic condition.

In this sense, we conclude this study by answering some questions and by formulating new ones:

• It is well known that the blood particles have a fundamental role in physiology and that abnormal cellular activities promote pathologies. The erythrocytes transport nutrients and oxygen. The platelets are activated and initiate the signalling pathway that goes from fibrinogen recruitment to the integrinbounding of some extracellular matrix compounds during hilling. Moreover, during inflammation, pro-inflammatory cytokines respond to an oxidative environment by recruiting monocytes, which differentiate into macrophages in atheroma development. Erythrocytes normally constitute 40% to 45% of the total blood volume, however, the effects erythrocytes on bio-mechanical responses in macro-circulation are commonly neglected. In the context of atherosclerosis, our results suggest that the effect of erythrocytes on shear stress profiles are important as proven both by computational modelling of atheroma development and by in vitro cell culture flow experiments, as shear stress profiles seem to be related to the regulation of cellular functions.

• Through this study, the fundamental question we have asked is at which extent the findings resulting from models of a disease are appropriate to be translated into clinical applications. As mentioned, both experimentation and computation have limitations. Therefore, what are the implications of simplifying assumptions in the clinical context? Moreover, if a certain criteria does not apply in humans, can it be neglected in either the experimental or the computational approaches used to understand the development of a certain disease? It is clear that the environment changes. Therefore, the concept of “realistic conclusion” might be associated to the appropriateness of the considerations made. Regulatory authorities as the Food and Drug Administration (FDA), the European Medicines Agency (EMA), the Committee for Medicinal Products for Human Use (CHMP), the Committee for Advanced Therapies (CAT), and the Pharmacovigilance Risk Assessment Committee (PRAC) have guidelines for translational and clinical research. To exemplify, these authorities have clear and strict rules for drug trials when moving from animal models to clinics. However, new discoveries from the basic research might be an important element in promoting new policies. Therefore, investigating the relevance of computational and experimental models of diseases might be a critical factor in biomedical research.

• Finally, how close are we of providing systems that efficiently deal with fully integrated multi-layer biological processes and predict and explain critically important biomedical issues? We actually do not have that answer. However, we anticipate our work to be the basis of a more sophisticated haemorheological model of atherosclerosis, to consistently support translational research and clinics.

Both current and future research involves the development of immunofluorescence assays for the assessment of the expression of the KLF2, the KLF4, and the IL-1b [38,39], in living cells, under multiphase flow condition. This is being combined to high performance computation [40], in a possibly adaptive environment, by using machine learning techniques. Moreover, the EA.hy926 is an immortalized cell line (aka. cancer cells), they do not behave as primary cells. Primary cell functions in cells line (e.g., flow alignment) are different from functions in primary cells. Therefore, 6 hours might be a short period to fully observe EA.hy926 cells alignment. Hence, we might compare the results here presented with experiments based on protein expression in HUVECs.