Biochemistry & Pharmacology: Open Access

Biochemistry & Pharmacology: Open Access
Open Access

ISSN: 2167-0501

Review Article - (2015) Volume 4, Issue 5

View PDF Download PDF

A Complete List of Kernels Used in Support Vector Machines

Jiapu Zhang1,2*
1Molecular Model Discovery Laboratory, Department of Chemistry and Biotechnology, Faculty of Science, Engineering & Technology, Swinburne University of Technology, Hawthorn Campus, Hawthorn, Victoria 3122, Australia
2Graduate School of Sciences, Information Technology and Engineering and Centre of Informatics and Applied Optimisation, Faculty of Science, The Federation University Australia, Mount Helen Campus, Mount Helen, Ballarat, Victoria 3353, Australia
*Corresponding Author: Jiapu Zhang, Molecular Model Discovery Laboratory, Department of Chemistry and Biotechnology, Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn Campus, Hawthorn, Victoria 3122, Australia, Tel: +61-3-9214 5596, +61-3-5327 6335, Fax: +61-423 487 360, +61-423 487 360 Email: ,

Abstract

In bioinformatics or chemoinformatics, we always need data mining of support vector machines (SVMs) for its large databases. Kernels play an important role in SVMs. Thus it is very necessary to list all the kernels of SVMs that we currently use.

<

Keywords: Bio/Chemoinformatics data; Data mining; Support vector machines (SVMs); Kernels; Hilbert space

With basic mathematical knowledge on Hilbert space and its reproducing kernel Hilbert space (RKHS) etc., it is not very difficult to understand the following (online-listed) kernels used in SVMs of data mining [1-5]:

(01). Polynomial (homogeneous) [1]: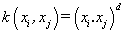image, where · denotes the dot product - an algebraic operation that takes two equal-length sequences of numbers and returns a single number, and d is an integer number.

(02). Polynomial (inhomogeneous) [1]: 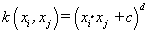image,c is a constant.

(03). Gaussian radial basis function (RBF) [1]: 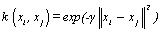image, for γ >0. Sometimes parametrized using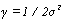 image

(04). Hyperbolic tangent (Sigmoid kernel) [1]: 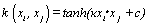image, for some (not every) κ > 0 and c < 0.

(05). Fisher kernel [1]: 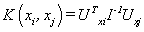image, where I is the Fisher information matrix and UX is the Fisher score.

(06). Graph kernel [1]: a kernel function that computes an inner product on graphs.

(07). String kernel [1]: a kernel function that operates on strings, i.e. finite sequences of symbols that need not be of the same length.

(08). Tree kernel [1]: the application of the more general concept of positive-definite kernel (a generalization of a positive-definite matrix) to tree structures.

(09). Path kernel [1].

(10). Linear kernel [1]:image [4]

(11). Fourier kernel [1]: 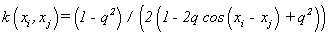image

(12). B-spline kernel [4]: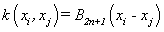image

(13). Cosine kernel [4]: 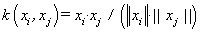image

(14). Multiquadric kernel [4]: 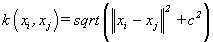image

(15). Wave kernel [4]: 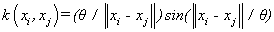image

(16). Log kernel [4]: 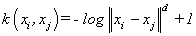image

(17). Cauchy kernel [4]: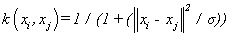image

(18). Tstudent kernel [4]: 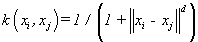image

(19). Thin-plate kernel [4]: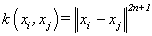image

(20). combination of some kernels of the above, e.g. 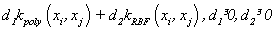image [2,5].

(21). Wavelet-SVM kernels: Harr kernel, Daubechies kernel, Coiflet kernel, Symlet kernel [3].

(22). In summary, in [6,7], there are a list of kernels:

• Definition 9.1 Polynomial kernel 286

• Computation 9.6 All-subsets kernel 289

• Computation 9.8 Gaussian kernel 290

• Computation 9.12 ANOVA kernel 293

• Computation 9.18 Alternative recursion for ANOVA kernel 296

• Computation 9.24 General graph kernels 301

• Definition 9.33 Exponential difiusion kernel 307

• Definition 9.34 von Neumann difiusion kernel 307

• Computation 9.35 Evaluating difiusion kernels 308

• Computation 9.46 Evaluating randomised kernels 315

• Definition 9.37 Intersection kernel 309

• Definition 9.38 Union-complement kernel 310

• Remark 9.40 Agreement kernel 310

• Section 9.6 Kernels on real numbers 311

• Remark 9.42 Spline kernels 313

• Definition 9.43 Derived subsets kernel 313

• Definition 10.5 Vector space kernel 325

• Computation 10.8 Latent semantic kernels 332

• Definition 11.7 The p-spectrum kernel 342

• Computation 11.10 The p-spectrum recursion 343

• Remark 11.13 Blended spectrum kernel 344

• Computation 11.17 All-subsequences kernel 347

• Computation 11.24 Fixed length subsequences kernel 352

• Computation 11.33 Naive recursion for gap-weighted

• subsequences kernel 358

• Computation 11.36 Gap-weighted subsequences kernel 360

• Computation 11.45 Trie-based string kernels 367

• Algorithm 9.14 ANOVA kernel 294

• Algorithm 9.25 Simple graph kernels 302

• Algorithm 11.20 All non-contiguous subsequences kernel 350

• Algorithm 11.25 Fixed length subsequences kernel 352

• Algorithm 11.38 Gap-weighted subsequences kernel 361

• Algorithm 11.40 Character weighting string kernel 364

• Algorithm 11.41 Soft matching string kernel 365

• Algorithm 11.42 Gap number weighting string kernel 366

• Algorithm 11.46 Trie-based p-spectrum kernel 368

• Algorithm 11.51 Trie-based mismatch kernel 371

• Algorithm 11.54 Trie-based restricted gap-weighted kernel 374

• Algorithm 11.62 Co-rooted subtree kernel 380

• Algorithm 11.65 All-subtree kernel 383

• Algorithm 12.14 Pair HMM kernel 407

• Algorithm 12.17 Hidden tree model kernel 411

• Algorithm 12.34 Fixed length Markov model Fisher kernel 427.

Acknowledgments

This research was supported by a Victorian Life Sciences Computation Initiative (VLSCI) grant numbered VR0063 on its Peak Computing Facility at the University of Melbourne, an initiative of the Victorian Government (Australia).

References

  1. Deng NY, Tian YJ, Zhang CH (2013) Support vector machines: optimization based theory, algorithms, and extensions. CRC Press, Taylor & Francis Group ISBN 978: 363.
  2. Ding LZ, Liao SZ (2012) KMA-$\alpha$: a kernel matrix approximation algorithm for support vector machines. J Computer Res & Development 49: 746-753.
  3. Tan K, Du PJ (2011) Wavelet support vector machines based on reproducing kernel Hilbert space for hyperspectral remote sensing image classification. Acta Geodaetica et Cartographica Sinica 40:142-147.
  4. Li ZY, Zhang WQ, He L, Liu J (2014) Speaker recognition with kernel based IVEC-SVM. Acta Automatica Sinica 40: 780-784.
  5. Lu Y, Wang HY, Tian N (2005) A support vector machine with a hybrid kernel and its application in underwater target recognition. Technical Acoustics 24: 144-147.
  6. Yang ZJ (2008) Kernel-based support vector machines. Computer Eng & Appl 44: 1-6.
  7. Song K, Zhang Z, Tong TP, Wu F (2012) Classifier assessment and feature selection for recognizing short coding sequences of human genes. See comment in PubMed Commons below J Comput Biol 19: 251-260.
Citation: Zhang J (2015) A Complete List of Kernels Used in Support Vector Machines. Biochem Pharmacol (Los Angel) 4:195.

Copyright: ©2015 Zhang J. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Top